2. 中国计量大学 信息工程学院, 杭州 310018
针对基于正交振幅调制(QAM)星座的未编码空时标记分集(USTLD)系统包络不恒定和频谱效率较低的问题,分别提出了相移键控星座的USTLD系统映射器设计方法和基于媒介调制(MBM)的USTLD系统,并对该系统的理论误码性能进行了分析.由于USTLD-MBM系统检测复杂度较高,故提出了该系统的低复杂度检测算法.仿真结果表明,在相同频谱效率的情况下,USTLD-MBM系统的误码性能优于USTLD系统.在USTLD-MBM系统中,球形译码算法的误码性能与最大似然算法几乎一致,复杂度降低了约50%.
2. College of Information Engineering, China Jiliang University, Hangzhou 310018, China
Aiming at the problem that the envelope of the uncoded space-time labeling diversity (USTLD) system based on quadrature amplitude modulation (QAM) constellation is not constant and the spectrum efficiency is low, the design method of mappers for phase shift keying (PSK) constellation and the USTLD system based on media based modulation (MBM) is proposed respectively. A bound of the average bit error probability of the proposed system is derived. Due to the high detection complexity of the USTLD-MBM system, a low complexity detection algorithm for the system is given. Simulations show that the error performance of the USTLD-MBM system is better than that of the USTLD system under the same spectral efficiency. In the USTLD-MBM system, the bit error performance (BER) of the sphere decoding algorithm is almost identical to the maximum likelihood (ML) algorithm, and the complexity is reduced by about 50%.
标记分集是一种将相同的信息比特映射到不同调制星座的技术,是改善系统误码性能的技术之一. 2016年Xu等[1]将标记分集应用于空时分组码(STBC, space-time block code)系统,被命名为未编码空时标记分集(USTLD, uncoded space-time labeling diversity). USTLD采用与Alamouti空时分组码(ASTBC, Alamouti space-time block code)相同的空时矩阵结构,不同的是,在USTLD中,不同时隙发送的调制符号采用同一种调制方式下的不同星座映射方式,若是两个时隙,则第2时隙两根发射天线发送的比特信息与第1个时隙一致,只不过采用第2种星座映射器产生调制符号. USTLD相比ASTBC系统无需编码和比特交织,使通信系统设计更灵活,复杂度相对降低,且在相同误码率下,信噪比(SNR, signal-to-noise ratio)得到显著增加,因此得到广泛应用[2-4].
以上研究都是假设两根发射天线的情况下,而为了进一步提高USTLD系统的误码性能和拓展研究范围,Ayanda等[5]研究了3根发射天线的USTLD系统,并提出了基于M阶正交振幅调制(QAM, quadrature amplitude modulation)星座映射器的启发式设计方法,但该映射器设计方法不能直接类推到M阶相移键控(PSK, phase shift keying)星座上.而从第5代甚至第6代移动通信系统的能耗角度考虑应选择使用恒包络的PSK调制,这是因为当前功率放大器的线性度严格限制着功率效率,而其线性度又与调制方式紧密相关,其中,包络为非常数的调制,如QAM,相比常数的调制,如PSK,对功率放大器的线性度要求更加苛刻.对此,提出了3根天线下基于PSK星座的USTLD系统映射器设计方法,该方法可以类推到大于3根天线的系统中.
媒介调制(MBM, media based modulation)是一种有效的提高频谱效率的方案.它是一种新提出的索引调制技术.其核心思想是使用带有射频反射镜单元的发射天线,通过控制反射镜的开/关状态来创建到接收器的不同的信道路径. MBM概念已在传统的空间调制(SM, spatial modulation)[6]和正交空间调制(QSM, quadrature spatial modulation)[7]和ASTBC系统[8]中使用.由以上文献可以看出,MBM的主要优点之一是具有高频谱效率,因为频谱效率与反射镜单元中的反射镜个数呈线性关系.从文献的仿真结果可以看出,在相同频谱效率的情况下,与MBM结合的系统可以获得更好的误码性能.
综上所述,提出了基于M-PSK星座的媒介索引调制USTLD(USTLD-MBM, uncoded space-time labeling diversity-media based modulation)系统设计方法,并对该系统的理论误码性能进行分析.而且针对USTLD-MBM系统最大似然(ML, maximum-likelihood)检测遍历搜索的高计算复杂度,提出了基于接收端球形译码的低复杂度检测算法.
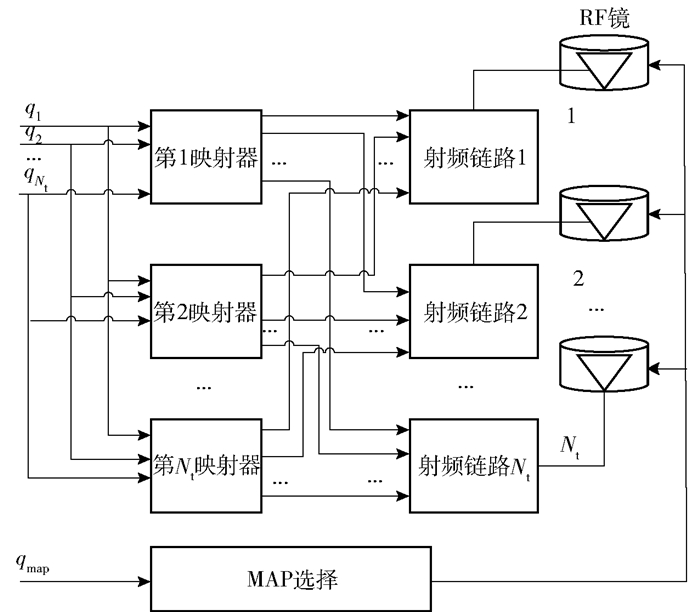
1 系统模型 1.1 USTLD-MBM系统考虑一个发射天线数为Nt,接收天线数为Nr的USTLD-MBM系统.每个发射天线具有与之相关联的射频(RF, radio frequency)镜单元,每个单元中包含mrf个RF镜.通过信息比特“1”或“0”分别控制RF镜的开或关,从而扰动发送天线附近的传输环境来随机化无线信道,进而改变整个传输路径.因此,对于一根天线,可由附近的mrf个RF镜产生Nm=2mrf种信道状态,而由mrf个信息比特来控制RF镜的一种开关状态叫做镜像激活模式(MAP, mirror activation pattern).
该系统发射端模型如图 1所示,输入比特qi=[qi, 1, qi, 2, …, qi, r1]表示用于映射调制符号的信息比特,i∈[1:Nt],r1=lbM.输入比特qi被送入映射器第k映射器(ΩkM),映射成复平面的星座点xqik,可以表示为xqik=ΩkM(qi),其中k表示第k个时隙,E{|xqik|}2=1.在该系统中,Ω1M是一个格雷映射器,ΩkM(k>1)是基于最小乘积距离最大化为目标设计的. xqik在第k个时隙由第i个发射天线发送,每个时隙发送的传输向量可以定义为xk=[xq1k, xq2k, …, xqNtk]T,因此,在该系统中传输的符号矩阵可以表示为Xsym=[x1, …, xk, …, xNt].输入比特qMAP=[qMAP1, qMAP2, …, qMAPr2]表示用于选择镜像激活模式的信息比特,其中r2=Nt×mrf,则可以得到第k时隙中发射天线的MAP索引值lik,其中lik∈{1, 2, …, Nm},则USTLD-MBM系统的频谱效率为η=lbM+ Nt×mrf.
|
图 1 USTLD-MBM系统发射端框图 |
USTLD-MBM系统传输矩阵X∈
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{X}} = \\ {\left[ {\begin{array}{*{20}{c}} {\mathop {\underbrace {0, \cdots ,x_{{q_1}}^1, \cdots ,0}_{{\rm{天线1}}}}\limits^{\mathop {l_1^1}\limits_ \downarrow } \left| {\mathop {\underbrace {0, \cdots ,x_{{q_2}}^1, \cdots ,0}_{{\rm{天线2}}}}\limits^{\mathop {l_2^1}\limits_ \downarrow } } \right| \cdots \left| {\mathop {\underbrace {0, \cdots ,x_{{q_{{N_{\rm{t}}}}}}^1, \cdots ,0}_{{\rm{天线}}{N_{\rm{t}}}}}\limits^{\mathop {l_{{N_{\rm{t}}}}^1}\limits_ \downarrow } } \right.}\\ \cdots \\ {\mathop {\underbrace {0, \cdots ,x_{{q_1}}^2, \cdots ,0}_{{\rm{天线1}}}}\limits^{\mathop {l_1^2}\limits_ \downarrow } \left| {\mathop {\underbrace {0, \cdots ,x_{{q_2}}^2, \cdots ,0}_{{\rm{天线2}}}}\limits^{\mathop {l_2^2}\limits_ \downarrow } } \right| \cdots \left| {\mathop {\underbrace {0, \cdots ,x_{{q_{{N_{\rm{t}}}}}}^2, \cdots ,0}_{{\rm{天线}}{N_{\rm{t}}}}}\limits^{\mathop {l_{{N_{\rm{t}}}}^2}\limits_ \downarrow } } \right.}\\ \cdots \\ {\mathop {\underbrace {0, \cdots ,x_{{q_1}}^{{N_{\rm{t}}}}, \cdots ,0}_{{\rm{天线1}}}}\limits^{\mathop {l_1^{{N_{\rm{t}}}}}\limits_ \downarrow } \left| {\mathop {\underbrace {0, \cdots ,x_{{q_2}}^{{N_{\rm{t}}}}, \cdots ,0}_{{\rm{天线2}}}}\limits^{\mathop {l_2^{{N_{\rm{t}}}}}\limits_ \downarrow } } \right| \cdots \left| {\mathop {\underbrace {0, \cdots ,x_{{q_{{N_{\rm{t}}}}}}^{{N_{\rm{t}}}}, \cdots ,0}_{{\rm{天线}}{N_{\rm{t}}}}}\limits^{\mathop {l_{{N_{\rm{t}}}}^{{N_{\rm{t}}}}}\limits_ \downarrow } } \right.} \end{array}} \right]^{\rm{T}}} \end{array} $ | (1) |
考虑到式(1)的一般形式,提出了2种不同的USTLD-MBM方案,它们在译码复杂度、频谱效率和误码性能之间提供了权衡.
方案1 在发送X的Nt个时隙中,所有发射天线采用相同的镜像激活模式,则频谱效率为
方案2 在发送X的每个时隙,采用相同的镜像激活模式,则频谱效率为η=mrf+lbM.
假设信道为瑞利快速衰落信道,则接收端的接收矩阵为
| $ {\mathit{\boldsymbol{y}}_k} = \sqrt {\frac{\rho }{{{N_{\rm{t}}}}}} {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{n}}_k} $ | (2) |
其中:ρ为信噪比;xk为传输矩阵X的第k列;Hk∈
接收端采用最大似然检测,通过遍历搜索USTLD-MBM接收向量的所有候选值,找到与接收向量欧式距离最小的星座点,从中恢复出信息比特,其表达式为
| $ \mathit{\boldsymbol{\hat X}} = \mathop {{\rm{arg}}}\limits_{{\mathit{\boldsymbol{X}}_k} \in \mathit{\boldsymbol{X}}} \mathop {{\rm{min}}}\limits_{{\rm{USTLD - MBM}}} \sum\limits_{k = 1}^{{N_{\rm{t}}}} {{{\left\| {{\mathit{\boldsymbol{y}}_k} - \sqrt {\frac{\rho }{{{N_{\rm{t}}}}}} {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{x}}_k}} \right\|}^2}} $ | (3) |
其中:XUSTLD-MBM表示USTLD-MBM系统所有候选值的集合,XUSTLD-MBM的大小与所选用的方案有关,采用方案1时,A=1;采用方案2时,A=Nt,则ML算法的搜索空间为MNt×NmA,由此可见,ML检测算法的搜索复杂度随着A的变化呈指数增长.
1.2 基于PSK星座的映射器设计由文献[1]可知,USTLD系统的误码性能取决于最小乘积距离,最大化最小乘积距离将使USTLD系统的误差性能最小化.这可以通过在USTLD系统中设计3个映射器来实现.第1映射器是一个格雷映射器,因此可以将优化描述为
| $ (\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2^M,\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3^M, \cdots ,\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{{N_{\rm{t}}}}^M) = \mathop {{\rm{argmax}}}\limits_{(x_{{q_1}}^k,\hat x_{{q_1}}^k) \in \chi } \left\{ {\mathop {{\rm{min}}}\limits_{x_{q1}^k \ne \hat x_{{q_1}}^k \in \chi } \prod\limits_{k = 1}^{{N_{\rm{t}}}} | x_{{q_1}}^k - \hat x_{{q_1}}^k{|^2}} \right\} $ | (4) |
其中:χ表示符号对(x2,x3, …, xNt)的所有组合.最优映射组合的求解代表了一个大规模的组合问题[2],对于需要3个映射器的系统,存在(M!)Nt-1种可能的映射器方案.
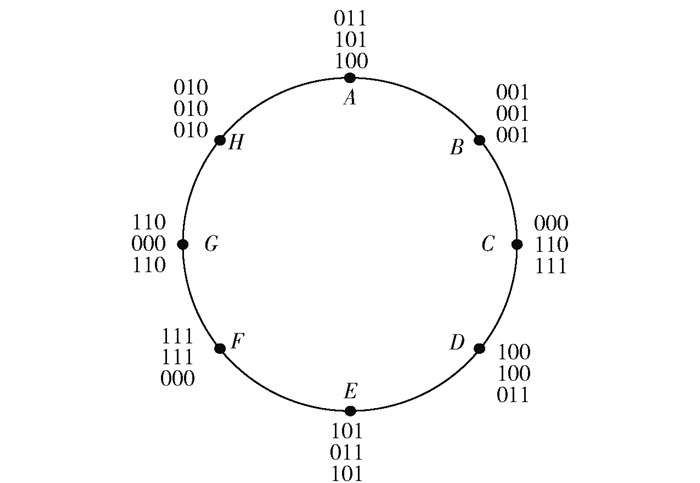
根据文献[1]提出的设计映射器的思想,在第2映射器、第3映射器中利用启发式方法尽可能地重组第1映射器的相邻星座点.基于8-PSK星座的3种映射器星座图如图 2所示. 图 2所示为3个映射器,每个星座点对应的输入比特中,上层为第1映射器,中层为第2映射器,下层为第3映射器.第1映射器为格雷映射,第2映射器中星座点A、C分别和E、G交换,第3映射器中星座点A、C分别和D、F交换,其他星座点沿用第1映射器的对应关系.当然这种映射方法并不是唯一的,映射的基本原则是将对角象限或对称轴上的比特对应关系进行交换,或最大或近似最大欧式距离的对应关系进行对换,该方法可以类推到大于3根天线的系统中.
|
图 2 基于8-PSK星座的3种映射器星座图 |
在瑞利快速衰落信道和ML检测的条件下,分析USTLD-MBM系统的平均误码率(ABEP,average bit error probability). ABEP可以定义为
| $ {P_{{\rm{ABEP}}}}(\rho ) \le \frac{1}{{{{({2^{{m_{{\rm{rf}}}}}})}^A}{M^{{N_{\rm{t}}}}}}}\sum\limits_\mathit{\boldsymbol{X}} {\sum\limits_{\mathit{\boldsymbol{\hat X}}} {\frac{{{N_{\mathit{\boldsymbol{X}} \to \mathit{\boldsymbol{\hat X}}}}P(\mathit{\boldsymbol{X}} \to \mathit{\boldsymbol{\hat X}})}}{{{N_{\rm{t}}}{\rm{lb}}M + A{m_{{\rm{rf}}}}}}} } $ | (5) |
其中:X为实际传输的矩阵,
| $ {\mathit{\boldsymbol{y}}_k} = \sqrt {\frac{\rho }{{{N_{\rm{t}}}}}} \sum\limits_{i = 1}^{{N_{\rm{t}}}} {\mathit{\boldsymbol{H}}_k^i} \mathit{\boldsymbol{x}}_{{q_i}}^k\mathit{\boldsymbol{e}}_{l_i^k}^i + {\mathit{\boldsymbol{n}}_k} $ | (6) |
其中Hki∈
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P(\mathit{\boldsymbol{X}} \to \mathit{\boldsymbol{\hat X}}|{\mathit{\boldsymbol{H}}_1}, \cdots ,{\mathit{\boldsymbol{H}}_{{N_{\rm{t}}}}}) = \\ P\left( {\sum\limits_{k = 1}^3 {\left\| {{\mathit{\boldsymbol{y}}_k} - \sqrt {\frac{\rho }{{{N_{\rm{t}}}}}} \sum\limits_{i = 1}^{{N_{\rm{t}}}} {\mathit{\boldsymbol{H}}_k^i} x_{{q_i}}^k\mathit{\boldsymbol{e}}_{l_i^k}^i} \right\|_{\rm{F}}^2} \le } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left\| {{\mathit{\boldsymbol{n}}_1}} \right\|_{\rm{F}}^2 + \cdots + \left\| {{\mathit{\boldsymbol{n}}_{{N_{\rm{t}}}}}} \right\|_{\rm{F}}^2} \right) \end{array} $ | (7) |
简化后,得出如下结论[1]
| $ \begin{array}{l} P(\mathit{\boldsymbol{X}} \to \mathit{\boldsymbol{\hat X}}|{\mathit{\boldsymbol{H}}_1}, \cdots ,{\mathit{\boldsymbol{H}}_{{N_{\rm{t}}}}}) = \\ Q\left( {\sqrt {\frac{\rho }{{12}}\sum\limits_{k = 1}^{{N_{\rm{t}}}} {\left\| {{\mathit{\boldsymbol{H}}_k}} \right\|_{\rm{F}}^2} \left\| {{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}}_k}} \right\|_{\rm{F}}^2} } \right) \end{array} $ | (8) |
其中
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Q(\varphi ) = \\ \frac{1}{{2c}}\left[ {\frac{1}{2}{\rm{exp}}\left( {\frac{{ - {\varphi ^2}}}{2}} \right) + \sum\limits_{k = 1}^{c - 1} {{\rm{exp}}} \left( {\frac{{ - {\varphi ^2}}}{{2{\rm{si}}{{\rm{n}}^2}\left( {\frac{{k\mathsf{π} }}{{2c}}} \right)}}} \right)} \right] \end{array} $ | (9) |
其中:c为用于收敛的迭代次数,在进行误码性能仿真时取c=10,可以得到无条件的成对错误概率为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{P}}(\mathit{\boldsymbol{X}} \to \mathit{\boldsymbol{\hat X}}) = \\ \frac{1}{{2c}}\left[ {\frac{1}{2}\sum\limits_{k = 1}^{{N_{\rm{t}}}} {{M_k}} \left( {\frac{1}{2}} \right) + \sum\limits_{i = 1}^{c - 1} {\sum\limits_{p = 1}^{{N_{\rm{t}}}} {{M_p}} } \left( {\frac{{ - {\varphi ^2}}}{{2{\rm{si}}{{\rm{n}}^2}\left( {\frac{{i\mathsf{π} }}{{2c}}} \right)}}} \right)} \right] \end{array} $ | (10) |
其中
为了减少USTLD-MBM系统中最大似然检测算法的计算复杂度,提出了接收端球形译码(Rx-SD,receiver centric-sphere decoding)检测算法[9],其基本思想是保存每次搜索的搜索深度和ML度量,一旦格点的欧式距离大于多维球体的半径,则停止搜索并丢弃该格点;一旦在球体内搜索到一个格点,则将球体半径更新为当前格点的欧式距离.当搜索完成后,保留的最后一个格点就是最优检测的格点.
式(3)中的ML检测算法表达式可以改写为
| $ [{\mathit{\boldsymbol{\hat I}}_{{\rm{MAP}}}},{\mathit{\boldsymbol{\hat X}}_{{\rm{sym}}}}] = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{{\rm{sym}}}} \in {\mathit{\boldsymbol{X}}_{{\rm{USTLD}}}}}\\ {{\mathit{\boldsymbol{I}}_{{\rm{MAP}}}} \in {\mathit{\boldsymbol{I}}_{{\rm{MBM}}}}} \end{array}} \sum\limits_{k = 1}^{{N_{\rm{t}}}} {{{\left\| {{\mathit{\boldsymbol{y}}_k} - \sqrt {\frac{\rho }{{{N_{\rm{t}}}}}} \mathit{\boldsymbol{H}}_{{\mathit{\boldsymbol{I}}_{{\rm{MAP}}}}}^k\mathit{\boldsymbol{x}}_{{\rm{sym}}}^k} \right\|}^2}} $ | (11) |
其中:Xsym表示传输的符号矩阵,XUSTLD表示所有可能的符号矩阵集合,则该集合大小为MNt. HIMAPk∈
假设MAP组合已确定,即HIMAP已知,则USTLD-MBM系统Rx-SD检测算法的数学表达式可以描述为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {{{\mathit{\boldsymbol{\hat X}}}_{{\rm{sym}}}}} \right] = \\ \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{{\rm{sym}}}} \in {\mathit{\boldsymbol{X}}_{{\rm{USTLD}}}}}\\ {{\mathit{\boldsymbol{I}}_{{\rm{MAP}}}} \in {\mathit{\boldsymbol{I}}_{{\rm{MBM}}}}} \end{array}} \left\{ {\sum\limits_{k = 1}^{{N_{\rm{t}}}} {{{\left\| {{\mathit{\boldsymbol{y}}_k} - \sqrt {\frac{\rho }{{{N_{\rm{t}}}}}} \mathit{\boldsymbol{H}}_{{\mathit{\boldsymbol{I}}_{{\rm{MAP}}}}}^k\mathit{\boldsymbol{x}}_{{\rm{sym}}}^k} \right\|}^2}} \le R_{{\rm{SD}}}^2} \right\} = \\ \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_{{\mathit{\boldsymbol{X}}_{{\rm{sym}}}} \in {\mathit{\boldsymbol{X}}_{{\rm{USTLD}}}}} \left\{ {\sum\limits_{b = 1}^L {\sum\limits_{k = 1}^{{N_{\rm{t}}}} {{{\left| {{y_k}(b) - \sqrt {\frac{\rho }{{{N_{\rm{t}}}}}} \mathit{\boldsymbol{H}}_{{\mathit{\boldsymbol{I}}_{{\rm{MAP}}}}}^k(b,:)\mathit{\boldsymbol{x}}_{{\rm{sym}}}^k} \right|}^2} \le } } } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R_{{\rm{SD}}}^2\} \end{array} $ | (12) |
其中:HIMAPk(b, :)为第k时隙信道增益子矩阵HIMAP的第b行;yk(b)为第b根接收天线在第k时隙接收到信号;L为搜索深度,1≤L≤Nr;RSD为初始半径,文献[9]给出的经验半径描述如RSD2=2αNrσn2,其中α是一个常数,它的选取是为尽可能地保证目标格点在预先设定的球体半径之中.
3.2 复杂度分析USTLD-MBM系统的ML检测算法、Rx-SD算法的计算复杂度的分析,以算法中包含的乘法作为比较(除法也认定为乘法).
ML检测算法:由式(3)可以看出,计算
Rx-SD检测算法:对于某一个候选向量,计算一层需要Nt(4Nt+2)次实数乘法,因此,Rx-SD的计算复杂度为CSD=(Nm)AMNt[Nt(4Nt+2)]Lavg,其中Lavg为平均搜索深度,则1≤Lavg≤Nr.
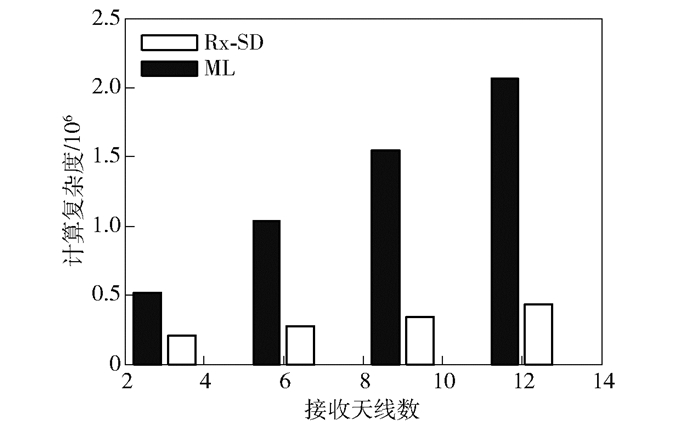
图 3所示为在Nt=3,mrf=3,信噪比ρ=10 dB,调制方式为8-PSK,改变接收天线Nr时,ML算法和Rx-SD算法的复杂度对比.从图中可以看出,Rx-SD算法复杂度相比ML算法至少降低50%,并且随着Nr的增大,2种算法复杂度差距更加明显.在大规模接收天线的情况下,可大幅度降低复杂度.
|
图 3 改变接收天线Nr的复杂度对比 |
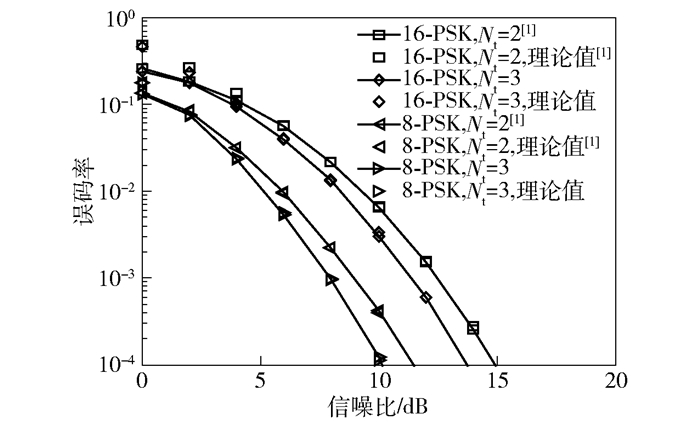
假设信道为瑞利快速衰落信道,在接收天线数Nr =3,调制方式为8-PSK时,图 4所示为发射天线数Nt =2[1]和Nt =3时USTLD系统的误码性能.从图 4中可以看出,在误码率为10-4时,3根发射天线的USTLD系统与2根发射天线的USTLD系统相比,误码性能有约1 dB的改善.并且,与调制方式为16-PSK时的误码性能相比,调制方式为8-PSK时的误码性能约改善3.5 dB,这是因为调制阶数越低,符号间的欧氏距离越大,系统的误码性能越好.从图中可以看出,参考文献[1]的USTLD系统理论误码率上界与仿真结果是拟合的.
|
图 4 基于PSK星座的USTLD系统误码性能 |
图 5所示为在Nt=3,Nr=3,频谱效率η=12时,USTLD系统与USTLD-MBM系统的误码性能.对于USTLD系统,调制方式采用16-PSK.对于USTLD-MBM系统,在方案1中,mrf=3,调制方式采用8-PSK;方案2中,mrf=1,调制方式同样采用8-PSK.在误码率为10-4时,与USTLD系统相比,USTLD-MBM系统的方案2得到约3 dB的性能提升.这是因为为了达到相同的频谱效率,USTLD系统需要使用更高阶的数字调制方式,从而影响系统的误码性能.同时,方案1的误码性能与方案2相比,误码性能改善约1 dB,这是因为在方案1中,所有发射天线的MAP索引相同,获得分集增益,改善误码性能.并且,式(5)推导的理论误码率上界在中高信噪比时与仿真结果是拟合的.
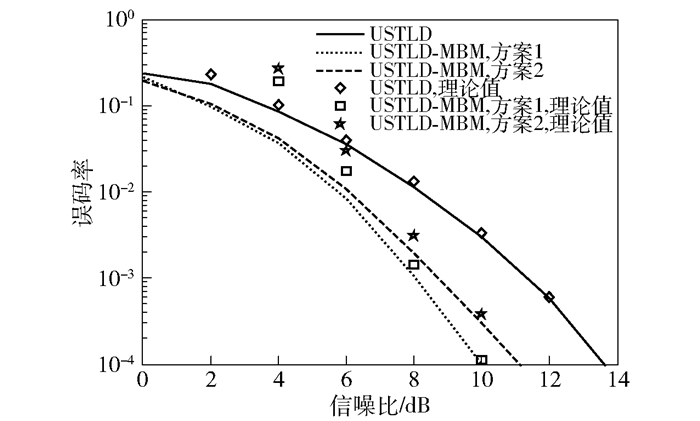
|
图 5 η=12 bpcu时的误码性能对比 |
图 6所示为频谱效率η=15时USTLD系统与USTLD-MBM系统的误码性能.对于USTLD系统,调制方式采用32-PSK.对于USTLD-MBM系统,在方案1中,mrf=6,调制方式采用8-PSK;方案2中,mrf=2,调制方式同样采用8-PSK.在误码率为10-4时,与USTLD系统相比,USTLD-MBM系统的方案2得到约7 dB的提升.由此可以看出,由于配置RF镜增加了USTLD-MBM系统的频谱效率,可以在使用低阶数字调制方式的情况下达到与USTLD系统相同的频谱效率.从图 5可以看出,方案1的误码性能与方案2相比,误码性能改善约1 dB.
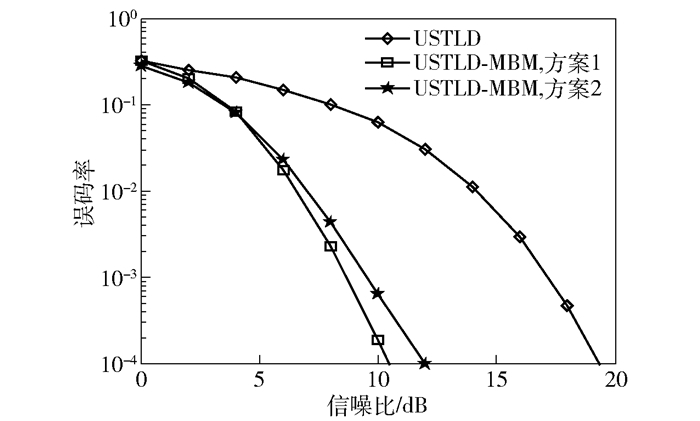
|
图 6 η=15 bpcu时的误码性能对比 |
图 7所示为频谱效率η=12和η=15时USTLD-MBM系统分别使用Rx-SD检测算法与ML检测算法时的误码性能对比.从图中可以看出,使用Rx-SD检测算法的系统误码性能与ML检测算法几乎一致.
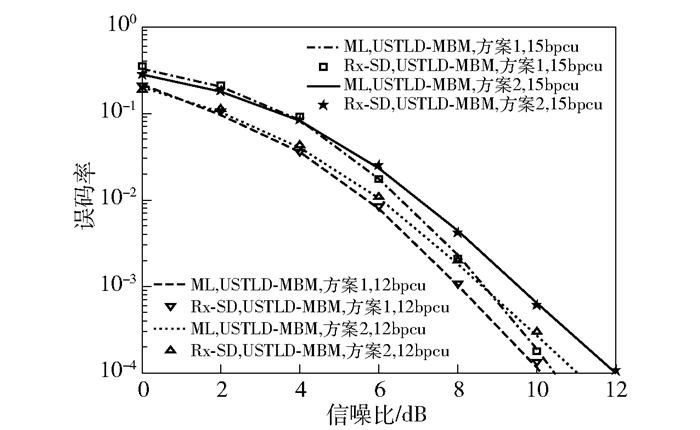
|
图 7 Rx-SD检测算法与ML检测算法误码性能对比 |
为了提高USTLD系统的频谱效率,对M-PSK调制下的USTLD-MBM系统的设计展开了深入研究,并给出了瑞利快速衰落信道下的蒙特卡洛仿真结果.利用联合边界对USTLD-MBM系统的ABEP进行了分析,在中高信噪比下与蒙特卡洛仿真结果高度吻合,并给出了该系统的低复杂度球形译码检测算法,使得系统的误码性能与ML下的性能几乎一致,且复杂度降低了约50%.根据USTLD目前的研究结果,可以很好的推广到5G系统中大规模MIMO系统下发射端的设计,以便提高5G系统的频谱效率、能耗效率,以及降低系统实现的复杂度.
| [1] |
Xu H, Govindasamy K, Pillay N. Uncoded space-time labeling diversity[J]. IEEE Communications Letters, 2016, 20(8): 1511-1514. DOI:10.1109/LCOMM.2016.2580503 |
| [2] |
Patel S S, Quazi T A, Xu H, et al. A genetic algorithm for designing uncoded space-time labelling diversity mappers[C]//2018 IEEE International Workshop on Signal Processing Systems (SiPS). Cape Town: IEEE, 2018: 77-82. https://www.researchgate.net/publication/330119914_A_Genetic_Algorithm_for_Designing_Uncoded_Space-Time_Labelling_Diversity_Mappers
|
| [3] |
Mughal S, Yang F, Umar R, et al. Space-time labeling diversity for WLAN based on 8-PSK modulation[C]//2018 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST). Islamabad: IEEE, 2018. https://www.researchgate.net/publication/323821294_Space-time_labeling_diversity_for_WLAN_based_on_8-PSK_modulation
|
| [4] |
Ramasila W L, Xu H. Improved error performance of a 3/4-Sezginer space-time block codes[J]. International Journal of Communication Systems, 2019, 32(13). |
| [5] |
Ayanda D, Xu H, Pillay N, et al. Uncoded M-ary quadrature amplitude modulation space-time labeling diversity with three transmit antennas[J]. International Journal of Communication Systems, 2018, 31(18). |
| [6] |
Naresh Y, Chockalingam A. On media-based modulation using RF mirrors[J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 4967-4983. DOI:10.1109/TVT.2016.2620989 |
| [7] |
Yildirim I, Basar E, Altunbas I. Quadrature channel modulation[J]. IEEE Wireless Communications Letters, 2017, 6(6): 790-793. DOI:10.1109/LWC.2017.2742508 |
| [8] |
Basar E, Altunbas I. Space-time channel modulation[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 7609-7614. DOI:10.1109/TVT.2017.2674689 |
| [9] |
Younis A, Renzo M D, Mesleh R, et al. Sphere decoding for spatial modulation[C]//2011 IEEE International Conference on Communications (ICC). Kyoto: IEEE, 2011. https://www.researchgate.net/publication/221168092_Sphere_Decoding_for_Spatial_Modulation
|



