2. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 西安 710071
为了缓解回程链路的压力,移动网络运营商(MNO)在其宏基站(MBS)覆盖范围内的热点地区上方灵活部署具有缓存能力的无人机(UAVs)作为空中基站.此外,多个内容提供商(CPs)渴望租用MBS和UAVs的缓存空间以主动缓存其流行视频,从而降低订阅用户的服务时延.但每个CP租赁缓存空间的意愿程度是私有的,这导致MNO和CPs间的信息不对称.为了解决此问题,提出了基于合同理论的缓存资源租赁机制以最大化MNO的效用.理论上推导出了合同的可行条件,继而将目标优化问题放松为凸规划问题,采用KKT条件求得缓存租赁的最优合同.仿真结果验证了所提出的无人机辅助第5代移动通信系统(5G)网络缓存租用机制的有效性,并讨论了UAVs的飞行高度对系统性能的影响.
2. The State Key Laboratory of Integrated Services Networks, Xidian University, Xi'an 710071, China
To alleviate the load of the backhaul link, a mobile network operator (MNO) temporarily deploys cache-enabled unmanned aerial vehicles(UAVs) as aerial base stations to offload the traffic from a macro base station (MBS). While several content providers (CPs) desire to rent the cache space at both the MBS and UAVs to proactively place their popular videos so that their subscribers can receive low-latency services. However, the willingness for cache renting is privately for each (CP), resulting in asymmetric information between the MNO and CPs. To overcome this problem, the contract theory is exploited to formulate the cache renting problem and to maximize the utility of MNO. The feasible conditions for the contract are derived, and the target optimization problem is relaxed to the convex programming problem. Finally, the KKT condition is utilized to solve the optimal contract for the cache renting. Experiments validate the effectiveness of the proposed cache renting mechanism in UAV-assisted the 5th generation of mobile communications system(5G) networks, and the influence of UAVs' flight altitude on system performance is discussed.
随着移动设备和社交多媒体业务的迅速发展,移动数据流量呈指数增长趋势.为了满足高度多样化在线数据流的需求,超密集小基站和边缘缓存的部署已成为第5代移动通信系统(5G,the 5th generation of mobile communications system)的2种前景技术[1].前者拉近基站和用户的距离,从而提高了频谱效率和网络容量.后者通过在本地基站缓存流行视频以大幅减少视频传输时延,同时减轻了回程链路压力[2].
目前,主动缓存已经成为无线网络中的研究热点. Le等[3]提出了一种新的无线网络切片缓存分区和定价机制. Guo等[4]研究了完全合作的缓存情况,集中器协助所有基站进行缓存决策.然而,现有的研究工作大多数局限于地面固定基站中的缓存设计,对于涉及临时热点、移动用户以及突发数据需求的场景,上述工作可能不合适或者成本效率低.与传统的地面基站相比,无人机具有部署灵活性、移动性以及空对地良好的信道特性等优势[5].因此,灵活部署具有缓存能力的无人机是动态缓存流行视频并有效地为突发热点区域中的移动用户提供高质量服务的完美解决方案.此外,用户热点检测在无人机的部署中起着至关重要的作用[6].基于移动用户的实时位置信息,移动运营商可以根据检测的用户热点及时调整UAV的位置,以覆盖尽可能多的用户.当热点区域中的业务大幅度减少,无人机将被迅速召回.
考虑一个由多个内容提供商(CPs,content providers)和一个移动网络运营商(MNO,mobile network operator)组成的商业化缓存租赁市场. MNO拥有一个具有缓存能力的宏基站(MBS, macro base station),且在该MBS的覆盖范围内检测到的热点上方临时部署多个具有缓存使能的UAVs.因此CPs可以在MBS和UAVs处租用缓存空间以本地存储流行视频,然后通过为其订阅用户提供低延迟服务来获利,而MNO则通过将缓存空间租赁给CPs来获利.虽然缓存资源共享既能缓解回程链路的压力又能降低用户获取内容的时延,但MNO和CPs的自私性以及两方的利益冲突性,引发了缓存租赁市场中的作弊和竞争问题.此外,缓存空间租用的意愿对于每个CP是私有的,这导致MNO和CPs之间的信息不对称.实际上,理性的CPs拒绝透露他们的私有信息,并且倾向于欺骗MNO以更低的价格租用更大的缓存空间.
合同理论[7]能够有效地设计非对称信息情景下经济参与者之间的激励机制.基于合同理论,Li等[8-10]研究了无线通信网络架构下的经济缓存.然而,这些工作要么缺乏CPs类型的具体定义,要么忽略了不同CPs之间流行视频分布的差异,导致区分CPs之间缓存租用意愿的无效性,恶化了MNO的效用.此外,合同理论尚未应用于设计激励机制以促进无人机辅助网络中的缓存租用.
因此,提出了无人机辅助5G网络中MNO的缓存租用机制.利用具有噪声的基于密度的空间聚类(DBSCAN, density-based spatial clustering of applications with noise)算法[6],MNO检测用户热点并实现缓存使能的UAV的准确部署.将缓存租用问题建模为合同制定模型,其中MNO针对每种类型的CP设计最优的缓存空间(MBS和UAVs)比例以及相应的租金以最大化其效用.特别地,将视频流行度分布和流量负载聚合为CPs类型的封闭表达式, 且受个人理性(IR, individual rational)和激励相容(IC, incentive compatible)约束每个内容提供商将选择与其类型匹配的合同项.从理论上推导出了合同的可行条件,继而将目标优化问题放松为凸规划问题,最后采用KKT(Karush Kuhn Tucker)条件求得缓存租赁的最优合同.仿真结果验证了所提出的方案有效地提高了MNO的效用,并激励CPs选择与其类型匹配的合同,且在UAVs的最优飞行高度下,系统性能达到最优.
1 系统模型缓存租赁网络系统如图 1所示,包括一个MNO、K个CPs,以及MNO的某个MBS覆盖范围内的U个移动用户,且CPs集和用户集分别记作
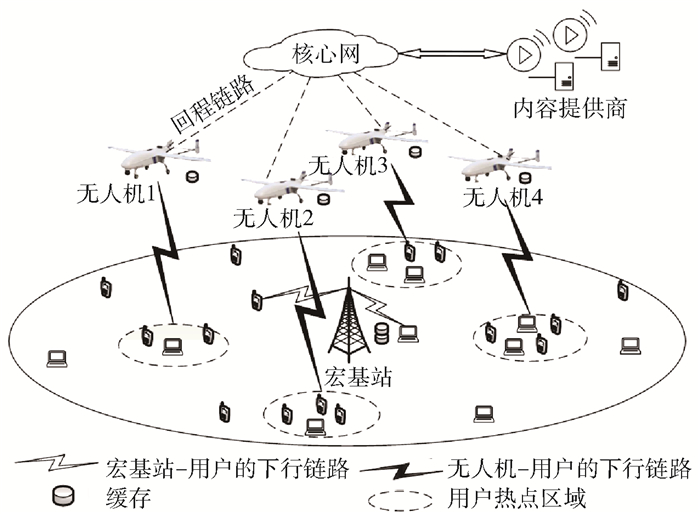
|
图 1 缓存租赁网络系统 |
假设所有视频文件的大小相同,均为s bit. MBS和每个UAV分别具有QM和QU个视频文件的缓存容量.根据自身的视频流行度分布和流量负载,CPs与MNO协商在MBS和UAVs处租用一定比例的缓存空间以主动缓存流行视频,从而为其订阅用户提供低时延服务.此外,MNO通过设计最优合同(φ, T),即(缓存比例,租金)合同集,旨在最大化每个时段内的收益.
1.1 信道模型频谱资源很大程度上影响着无人机对热点地区的流量卸载性能.假设总的带宽资源为B,由UAV集
无人机和移动用户之间的空对地无线通信信道主要由视距链路(LoS, line of sight)和非视距链路(NLoS, none-line of sight)两部分组成[5],其中LoS链路的传播概率为
| $ {P_{{\rm{LoS}}}}(\delta ) = \frac{1}{{1 + a{\rm{exp}}( - b[\delta - a])}} $ | (1) |
其中:a和b是由环境(如市区郊区等)的常数;
| $ \left. \begin{array}{l} \begin{array}{*{20}{c}} {{{\bar L}_{\rm{U}}}(d) = {P_{{\rm{LoS}}}}(\delta ){L_{{\rm{LoS}}}}(d) + }\\ {[1 - {P_{{\rm{LoS}}}}(\delta )]{L_{{\rm{NLoS}}}}(d)} \end{array}\\ \begin{array}{*{20}{l}} {{L_{{\rm{LoS}}}}(d) = {{(4\pi fd/c)}^2}{\eta _{{\rm{LoS}}}}}\\ {{L_{{\rm{NLoS}}}}(d) = {{(4\pi fd/c)}^2}{\eta _{{\rm{NLoS}}}}} \end{array} \end{array} \right\} $ | (2) |
其中:f为信道载波频率,c为光速;LLoS(d)和LNLoS(d)分别是LoS和NLoS的链路损耗;ηLoS和ηNLoS是取决于环境的平均附加损耗.
因此,用户i从UAVn处接收到的信干噪比(SINR,signal-to-interference-plus-noise ratio)为
| $ \gamma _{\rm{U}}^{ni} = \frac{{P_{{\rm{r,U}}}^{ni}}}{{\sum\limits_{{n^\prime } \in \mathscr{N} {\backslash _n}} {P_{{\rm{r,U}}}^{{n^\prime }i}} + P_{{\rm{r,M}}}^i + {\sigma ^2}}} $ | (3) |
其中:Pr, Uni表示用户i从UAVn接收的信号功率,
由于地面宏基站和用户之间存在高楼大厦等地面建筑物的遮挡,所以两者间的下行信道仅考虑NLoS链路.那么,用户i从MBS处接收到的SINR可以表示为
| $ \gamma _{\rm{M}}^i = \frac{{P_{{\rm{r,M}}}^i}}{{\sum\limits_{n \in \mathscr{N}} {P_{{\rm{r,U}}}^{ni}} + {\sigma ^2}}} $ | (4) |
其中:Pr, Mi表示用户i从MBS接收到的信号功率,
假设每个用户可以在MBS和N台UAVs中自主选择接入以获得最佳的SINR通信服务.因此,有必要找出某个UAV在哪个区域能够提供比其他UAVs或MBS更好的SINR,并且将某个UAV能提供最好SINR的区域记作该UAV的有效卸载区域.同时,将由MBS或UAVn服务的用户集分别记作
根据式(3)、式(4),用户i接收到的数据速率为
| $ {R_{ni}} = \frac{B}{{|{\mathscr{U}_n}|}}{\rm{log}}[1 + \gamma ({d_{ni}})] $ | (5) |
其中:n=0表示用户i由MBS服务,γ(d0i)=γMi;n∈
CPs租用缓存空间的意愿度主要取决于其视频流行分布和流量负载,这些信息是每个CP私有的,MNO不能轻易获取.由于视频库、营销策略和推荐策略[11]不同,不同CPs的视频流行度分布和用户负载(订阅用户数量)存在差异.基于上述2种因素,CPs对租用缓存空间有不同的激励水平.
1.2.1 视频的流行度假设所有CPs有自己的视频库,且对于CPk,∀k∈
| $ {p_{kl}} = \frac{{{l^{ - {\alpha _k}}}}}{{\sum\limits_{j = 1}^L {{j^{ - {\alpha _k}}}} }},\forall l \in \{ 1,2, \cdots ,L\} $ | (6) |
其中0 < αk < 1反映了用户对CPk的视频请求的集中程度,αk越大意味着视频请求更集中于高排名的视频.根据齐夫定律,流行度越高的视频可以为CP带来更大的价值,因此可以定义CPk的第l排名视频的潜在价值与其请求概率成正比,即
| $ {w_{kl}} = \eta {p_{kl}} = \eta \frac{{{l^{ - {\alpha _k}}}}}{{\sum\limits_{i = 1}^L {{j^{ - {\alpha _k}}}} }},\forall l \in \{ 1,2, \cdots ,L\} $ | (7) |
其中η为常数.则CPk所有视频的期望价值为
| $ {\bar w_k} = \sum\limits_{l = 1}^L {{w_{kl}}} {p_{kl}} = \sum\limits_{l = 1}^L \eta {\left( {\frac{{{l^{ - {\alpha _k}}}}}{{\sum\limits_{j = 1}^L {{j^{ - {\alpha _k}}}} }}} \right)^2},\forall k \in \mathscr{K} $ | (8) |
式(8)对αk求导,得w′(αk)>0,表明视频请求集中度越高(αk越大)的CP,其视频的期望价值越高.
1.2.2 用户负载由于CPs提供的视频质量、视频种类和收费标准不同,用户对CPs的偏好呈现出多样性.因此,一些CPs比其他CPs拥有更多的订阅用户.假设用户在CPs之间的订阅分布为q={q1, q2, …, qK},其中qk, ∀k∈
本研究提出对CP的类型进行具体定义,旨在充分刻画CP租用缓存空间的意愿度.
定义1 根据视频流行度分布αk和用户负载qk确定CPk的类型为
| $ {\theta _k} = {q_k}{\bar w_k} = {q_k}\sum\limits_{l = 1}^L \eta {\left( {\frac{{{l^{ - {\alpha _k}}}}}{{\sum\limits_{j = 1}^L {{j^{ - {\alpha _k}}}} }}} \right)^2} $ | (9) |
注意,式(9)中的定义是合理的,并且表明较大的CP类型θk,也即较大的αk(更集中的视频请求)和较高的qk(更高的用户负载),代表着该CP更渴望从MNO租用更多的缓存空间,以本地化服务更多的用户并获得更多利润.
根据定义1,集合
理性的CPs拒绝透露私人类型并趋向于欺骗MNO从而能够以更低的租金租赁到更多的缓存空间.面对信息不对称问题,MNO必须制定合同集Φ={(φk, Tk), ∀k∈
通过租用φk比例的MNO缓存空间,θk类型的CP可以分别在MBS和每个UAV上缓存φkQM和φkQU流行视频文件,继而为请求这些已缓存视频的用户提供本地化服务,降低服务时延.因此,将θk类型CP的效用定义为
| $ {U_k} = \sum\limits_{n = 0}^N {\sum\limits_{i \in {U_n}} {{\theta _k}} } {\varphi _k}{Q_n}{R_{ni}} - {T_k} $ | (10) |
其中:第1个求和项代表θk类型的CP在MBS (n=0)和N个UAV(n∈
| $ {U_k} = {\theta _k}{\varphi _k}Q - {T_k} $ | (11) |
虽然MNO不清楚每个CP的具体类型,但对CP为θk类型的先验概率πk掌握一定的统计信息,其中πk∈[0, 1],
| $ {U_{{\rm{MNO}}}} = \sum\limits_{k = 1}^K {{\pi _k}} [{T_k} - C({\varphi _k})] $ | (12) |
其中C(φk)=c(φk)+C0表示MNO为θk类型的CP提供服务所花费的运营成本,C0是部署UAV的固定成本,c(φk)是一个非负的缓存成本并随着缓存比例φk递增.进一步假设c(φ)在缓存比例较高的情况下比在缓存比例较低的情况下增长更快,即c″(φ)>0.
2.3 合同建模为了激励CPs租用缓存空间,合同条款应满足IR约束,即每种类型的CP通过接受与其类型匹配的合同条款能够确保得非负效用,即
| $ {\theta _k}{\varphi _k}Q - {T_k} \ge 0,\forall k \in \mathscr{K} $ | (13) |
此外,θk类型的CP只有选择与自己类型匹配的合同项(φk, Tk)才能获得最大效用,而不会选择为其他类型设计的合同项(φk′, Tk′),因此合同必须满足IC约束,即
| $ {\theta _k}{\varphi _k}Q - {T_k} \ge {\theta _k}{\varphi _{{k^\prime }}}Q - {T_{{k^\prime }}},\forall k,{k^\prime } \in \mathscr{K} ,k \ne {k^\prime } $ | (14) |
除了IR和IC约束外,合同条款还需满足租赁缓存空间大小的容量限制,另外MBS和UAV缓存的视频个数应为整数,即
| $ {\sum\limits_{k = 1}^K {{\pi _k}} {\varphi _k} \le 1} $ | (15) |
| $ {{\varphi _k}{Q_n} \in \mathbb{N},\forall k \in \mathscr{K},n \in \{ 0 \cup \mathscr{N}\} } $ | (16) |
然后,最优合同设计问题可表示为MNO的效用最大化问题,即
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{max}}}\limits_{\{ ({\varphi _k},{T_k}),k \in \mathscr{K}\} } \sum\limits_{k = 1}^K {{\pi _k}} [{T_k} - C({\varphi _k})]}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}(13),(14),(15),(16),0 \le {\varphi _k} \le 1} \end{array} $ | (17) |
接下来,在解决式(17)中的问题之前,需要简化K个IR和K(K-1)个IC约束.因此,研究缓存租用策略的性质,并提出了以下引理.
引理1 问题(17)中的IR和IC约束可以简化为
1) φK < … < φ1,
2) TK≤θKφKQ,
3) θk-1(φk-φk-1)Q < Tk-Tk-1 < θk(φk-φk-1)Q, ∀k∈{2, …, K}.
证明见附录A.在引理1中,1)和2)是IR约束的充分必要条件,而1)和3)是IC约束的充分必要条件. 1)暗示MNO必须为具有更高类型的CP提供更多的缓存空间.对于1),如果最低类型θK的CP可以从交易中获得非负效用,则所有其他高类型CP的IR约束将自动保持,因此得到2). 3)表示如果IC约束在第k类型和第(k-1)类型的CP间成立,则在第k类型和所有其他类型的CP间亦成立.
根据引理1,问题(17)就可以重新表示为
| $ \begin{array}{l} \mathop {{\rm{max}}}\limits_{\{ ({\varphi _k},{T_k}),k \in \mathscr{K}\} } \sum\limits_{k = 1}^K {{\pi _k}} [{T_k} - C({\varphi _k})]\\ {\rm{ s}}{\rm{.t}}{\rm{. }}1),2),3),(15),(16),0 \le {\varphi _k} \le 1. \end{array} $ | (18) |
为了得出MNO的最佳交易策略,首先去除缓存空间比例φk的单调性约束,接着验证所获得的解是否满足该约束.因此,如定理1中所示,可以通过求解问题(18)来获得最优租金策略Tk*, k∈
定理1 给定分配给每种类型CP的缓存空间比例,即φk, ∀k∈
| $ T_k^* = \left\{ {\begin{array}{*{20}{l}} {T_{k + 1}^* + {\theta _k}({\varphi _k} - {\varphi _{k + 1}})Q,\quad {\rm{ 若 }}k = 1,2, \cdots ,K - 1}\\ {{\theta _k}{\varphi _k}Q,\quad {\rm{ 若 }}k = K} \end{array}} \right. $ | (19) |
证明见附录B.
此外,将Tk*, k∈
定理2 MNO租赁给θk类型CP的最佳缓存空间比例,即φk*,应为
| $ \varphi _k^* = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\pi _k}\hat \varphi _k^* + {\pi _{k + 1}}\hat \varphi _{k + 1}^*}}{{{\pi _k} + {\pi _{k + 1}}}},\quad {\rm{ 若 }}\hat \varphi _k^* < \hat \varphi _{k + 1}^*}\\ {\hat \varphi _k^*,\quad {\rm{ 若 }}\hat \varphi _k^* \ge \hat \varphi _{k + 1}^*} \end{array}} \right. $ | (20) |
证明见附录C.此处
| $ \left. {\begin{array}{*{20}{l}} {Z_k^\prime ({\varphi _k}) + \lambda {\pi _k} + {\lambda _k} = 0,\forall k \in \mathscr{K}}\\ {{\lambda _k}{\varphi _k} = 0,\forall k \in \mathscr{K}}\\ {\sum\limits_{k = 1}^K {{\pi _k}} {\varphi _k} = 1} \end{array}} \right\} $ | (21) |
其中:Z′k(φk)是Zk(φk)=πkθkφkQ+
对于式(16)中的约束,在MNO将最优合同集Φ={(φk*, Tk*), ∀k∈
在仿真中,存在 K=10种类型的CPs,且这些CPs的视频请求集中度参数按降序排列为α=(0.55, 0.5, 0.45, 0.4, 0.35, 0.3, 0.25, 0.2, 0.15, 0.1),相应的用户负载分布为q=(0.18, 0.16, 0.14, 0.12, 0.1, 0.08, 0.07, 0.06, 0.05, 0.04).无人机辅助网络系统相关的其他仿真参数的值如表 1所示.结合泊松点过程(PPP,passion point process)与泊松簇过程(PCP,passion cluster process)模拟宏基站MBS覆盖范围内用户分布.然后根据最大移动距离为10 m的随机游走获取下一个时段中的用户分布,且通过DBSCAN算法[6]检测N=4个热点区域,MNO灵活地在每个热点的中心上方高度H处部署一台具有缓存能力的UAV,并通过回程链路与核心网相连.
|
|
表 1 仿真参数 |
首先,为验证合同的可行性,将运算成本设定为C(φk)=c(φk)+C0=gφk2+C0,其中g是边际缓存成本参数. 图 2显示了10种类型的CP各自选择不同合同条款后的期望效用,不难发现,CPs选择与其类型匹配的合同条款会获得正效用和最大效用,如若选择其他的合同条款会遭受效用损失.此外,高类型的CPs渴望租用更高比例的缓存空间,并获得更大的效用.上述结论满足单调性以及IC约束,验证了所求合同的可行性.
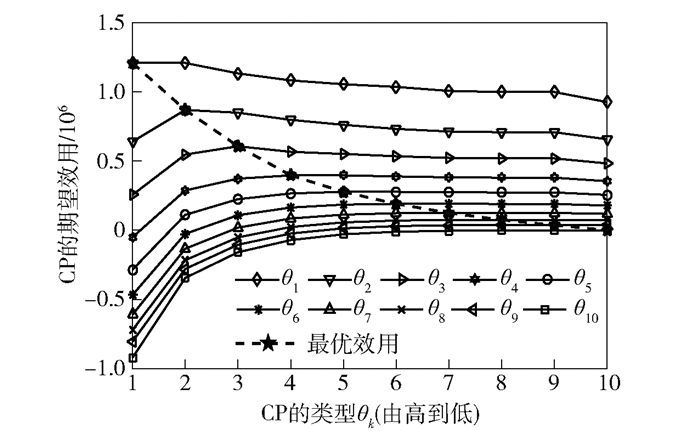
|
图 2 合同可行性验证(CP期望效用) |
然后,为了评估所提出的基于合同的缓存租赁机制的系统性能,将从CPs和MNO的效用层面与2个基准机制进行比较,即均匀分配[3]和统一定价分配[13].其中,均匀分配机制指的是在CPs之间平均分配缓存空间,统一定价分配机制指的是以统一的单价租用缓存空间. 图 3(a)表明,提出的方案在高类型CPs处的期望效用优于2种基准方案,相比之下,在低类型CPs处的效用稍逊.这是由于缓存容量的限制,并且在提出的机制中MNO倾向于租赁更多的缓存空间给更高类型的CPs,以获取更多的收益.同时,此现象也揭示了CPs之间缓存租用的相互依赖性.具体地,当某个高类型的CPs租用的缓存空间增加,该类型CPs的期望效用增大,而留给其他低类型CPs的剩余缓存空间减少,他们的期望效用会相应地减少.由图 3(b)可以发现,对比3种方案,在提出的方案中MNO的期望效用达到最高.这是因为合同机制充分考虑了CPs的异构性,能够区分不同CPs缓存空间租用的意愿度,从而进一步优化MNO的效用.此外,当缓存成本参数g增加时,边际缓存空间的开销越大,迫使CPs减少租用的缓存空间,所以MNO的期望效用降低.
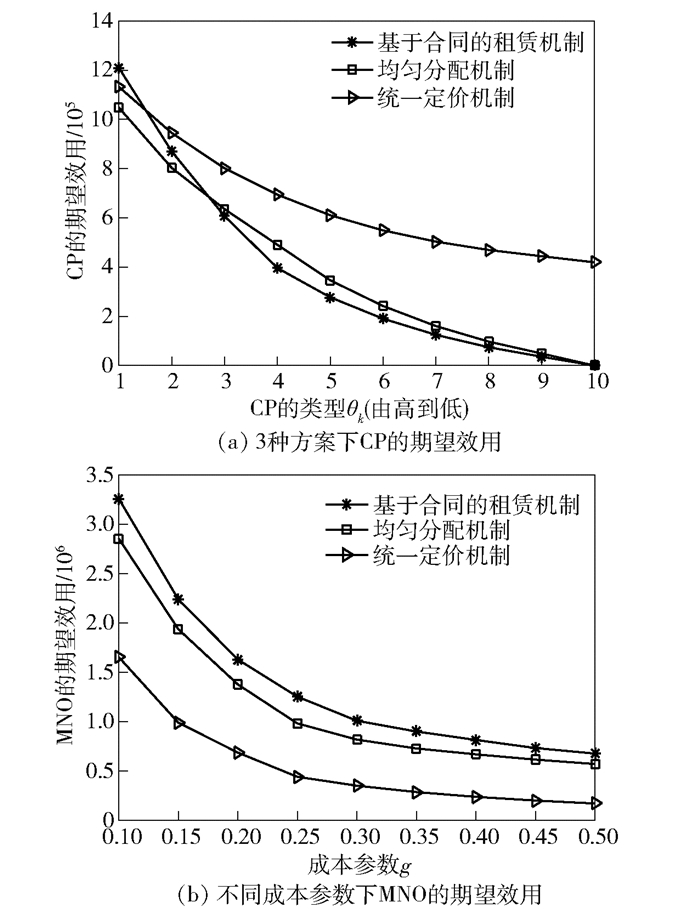
|
图 3 对比仿真下的系统性能分析 |
最后,探讨了UAV的飞行高度H对系统性能的影响.由于UAV的高度会影响LoS链路的概率以及链路损耗,从而对用户接收到的SINR产生影响,进而影响UAVs对热点区域的有效卸载范围.固定UAV、MBS的发射功率和其他参数. 图 4 (a)~(c)显示,当UAV的高度单调增加时,这些UAVs的卸载范围首先扩展然后收缩.如图 4(b)所示,当H=251 m时,UAVs达到最大卸载区域,即覆盖最大数量的移动用户.此外,图 4(d)展示了UAV的飞行高度H对MNO期望效用的影响,随着H的增加,MNO的期望效用先增加后减少,此趋势与UAV的卸载区域大小的变化一致,且H接近250 m时,MNO能够实现最大期望效用.因为当UAV飞行在最佳高度时,卸载流量达到最大并实现UAVs和MBS间的负载均衡,从而最高效率地利用MBS和UAVs的缓存和传输资源.
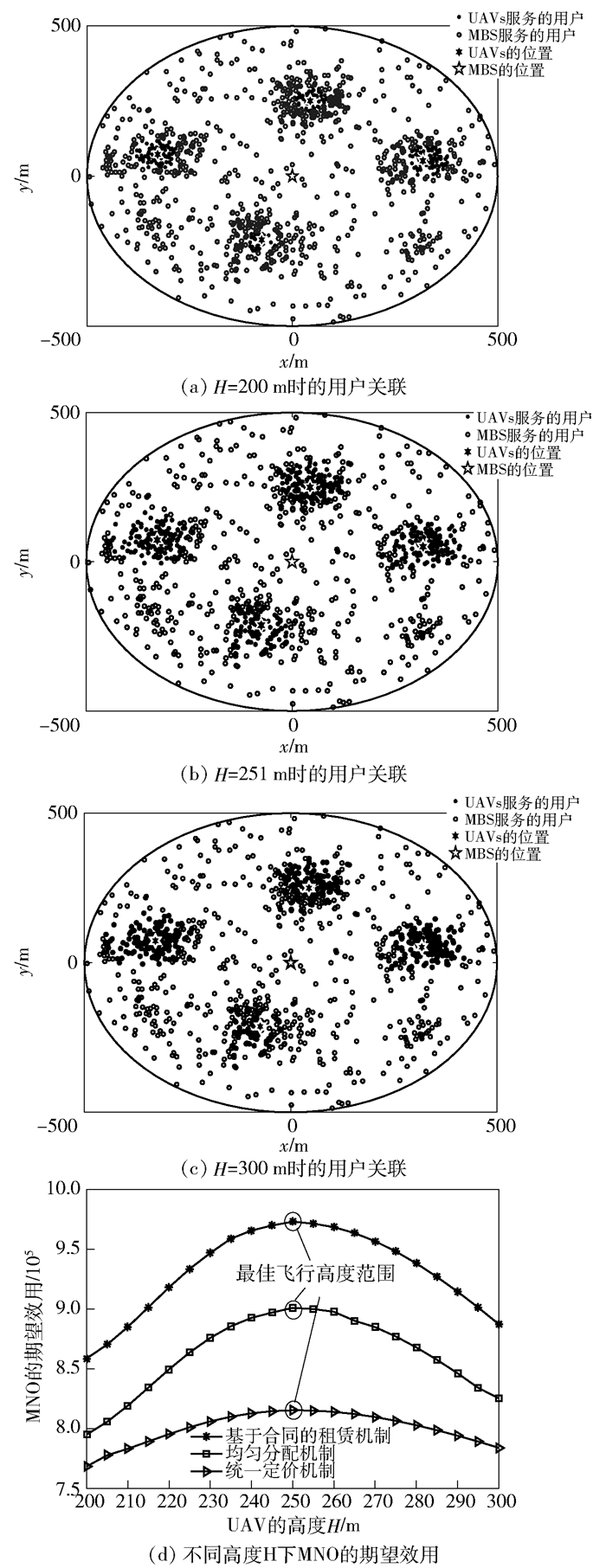
|
图 4 UAV的飞行高度对系统性能的影响 |
研究了5G网络中的缓存租赁问题,MNO通过灵活地在热点区域部署具有缓存能力的UAV,以卸载MBS的部分流量.结合视频流行度分布和用户负载量对异构CPs进行类型划分.基于合同理论,提出了缓存租用激励机制,以激励CPs选择与自身类型匹配的合同项来缓存流行视频并获得最大的效用.仿真结果验证了所提出的基于合同的缓存租赁机制的有效性,讨论了UAVs的飞行高度对系统性能的影响,且存在最优飞行高度使系统性能最佳.
附录A 引理1的证明
注意,1)和2)是IR约束的充分必要条件,而1)和3)是IC约束的充分必要条件.
1) 的证明.假设类型θk和类型θl的CP(k≠l)的合同项分别为(φk, Tk)和(φl, Tl).根据IC约束:
| $ {\theta _k}{\varphi _k}Q - {T_k} > {\theta _k}{\varphi _l}Q - {T_l} $ | (22) |
以及
| $ {\theta _l}{\varphi _l}Q - {T_l} > {\theta _l}{\varphi _k}Q - {T_k} $ | (23) |
结合式(22)和式(23)得到(θk-θl)(φk-φl)Q>0,因此φk>φl当且仅当θk>θl,表明应该租赁更多的缓存空间给视频价值更高的CP.此外,结合约束:0≤φk≤1,对θK < … < θ1,有0≤φK < … < φ1≤1.
2) 的证明.由于θk>θl,可以得到Uk=θkφkQ-Tk>θkφlQ-Tl>θlφlQ-Tl=Ul,表示更高类型的CP通过租赁缓存得到的收益越大.
此外,对于θK < … < θ1,有U1>…>UK.因此,如果UK≥0,则有Uk≥0, ∀k < K;在这种情况下,K个类型CP的IR约束可以减少为UK≥0,即TK≤θKφKQ.
3) 的证明.邻下激励约束(LDIC,local downward IC constraints):对于θK < … < θ1,如果IC约束在任何k类型和(k-1)类型的CP之间成立,则有Uk(φk, Tk)>Uk(φk-1, Tk-1),Uk-1(φk-1, Tk-1)>Uk-1(φk-2, Tk-2),即
| $ {{\theta _k}{\varphi _k}Q - {T_k} > {\theta _k}{\varphi _{k - 1}}Q - {T_{k - 1}}} $ | (24) |
以及
| $ {{\theta _{k - 1}}{\varphi _{k - 1}}Q - {T_{k - 1}} > {\theta _{k - 1}}{\varphi _{k - 2}}Q - {T_{k - 2}}} $ | (25) |
因为对θk-1 < θk-2,有φk-1 < φk-2.再结合θk < θk-1和式(25),可以得到
| $ {\theta _k}({\varphi _{k - 1}} - {\varphi _{k - 2}})Q > {\theta _{k - 1}}({\varphi _{k - 1}} - {\varphi _{k - 2}})Q > {T_{k - 1}} - {T_{k - 2}} $ | (26) |
结合式(24)和式(26)得: θkφkQ-Tk>θkφk-2Q-Tk-2,即Uk(φk, Tk)>Uk(φk-2, Tk-2),表明向下IC约束在k类型和(k-2)类型的CP之间也成立.通过归纳法,可以得出结论:如果在k类型和(k-1)类型CP之间向下IC约束成立,那么在k类型和所有(k-2),…,1类型之间也成立.
注意,邻上激励约束(LUIC, local upward IC constraints)的证明过程和LDIC证明类似,故省略.
附录B 定理1的证明
首先,式(19)满足Tk*≤Tk+1*+θk(φk-φk+1)Q,也即满足引理1中的IR和IC约束.接下来,通过反证法证明式(19)中的租金最大化了式(18)中定义的MNO的效用.给定缓存分配比例,可知MNO的效用取决于
附录C 定理2的证明
式(19)中的租金可以重写为
| $ T_k^* = T_K^* + \sum\limits_{i = k}^K {{\varDelta _i}} $ | (27) |
其中:当k=K时,Δi=0;Δi=θk(φk-φk+1)Q,当0 < i < K.将式(27)代入并删除在MBS和UAVs缓存的视频的单调性条件和整数约束,得到放松的优化问题,即
| $ \begin{array}{l} \mathop {{\rm{max}}}\limits_{\{ {\varphi _k},\forall k \in \mathscr{K} \} } \sum\limits_{k = 1}^K {{Z_k}} ({\varphi _k})\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (15),0 \le {\varphi _k} \le 1 \end{array} $ | (28) |
这里
显然,所有Zk(φk), ∀k∈
| $ U = \sum\limits_{k = 1}^K {{Z_k}} ({\varphi _k}) + \lambda \left( {\sum\limits_{k = 1}^K {{\pi _k}} {\varphi _k} - 1} \right) + \sum\limits_{k = 1}^K {{\lambda _k}} {\varphi _k} $ | (29) |
其中λ和λk均为拉格朗日乘数.将式(29)分别对φk、λ以及λk(∀k∈
注意,如果
| $ \varphi _i^* = \varphi _{i + 1}^* = \cdots = \varphi _j^* = \frac{{{\pi _i}\hat \varphi _i^* + {\pi _{i + 1}}\hat \varphi _{i + 1}^* + \cdots + {\pi _j}\hat \varphi _j^*}}{{{\pi _i} + {\pi _{i + 1}} + \cdots + {\pi _j}}}. $ |
另一方面,对于{
| [1] |
Goian H S, Al-Jarrah O Y, Muhaidat S, et al. Popularity-based video caching techniques for cache-enabled networks:a survey[J]. IEEE Access, 2019, 7: 27699-27719. DOI:10.1109/ACCESS.2019.2898734 |
| [2] |
Bastug E, Bennis M, Debbah M. Living on the edge:the role of proactive caching in 5G wireless networks[J]. IEEE Communications Magazine, 2014, 52(8): 82-89. DOI:10.1109/MCOM.2014.6871674 |
| [3] |
Le T H T, Tran N H, Vo P L, et al. Contract-based cache partitioning and pricing mechanism in wireless network slicing[C]//IEEE Global Communications Conference. Singapore: IEEE Press, 2017: 1-6.
|
| [4] |
Guo Yinghao, Duan Lingjie, Zhang Rui. Cooperative local caching under heterogeneous file preferences[J]. IEEE Transactions on Communications, 2017, 65(1): 444-457. |
| [5] |
Lyu Jiangbin, Zeng Yong, Zhang Rui. UAV-aided offloading for cellular hotspot[J]. IEEE Transactions on Wireless Communications, 2018, 17(6): 3988-4001. DOI:10.1109/TWC.2018.2818734 |
| [6] |
Masdung F, Septriani, Meiriza A, et al. Spatio-temporal analysis of south Sumatera hotspot distribution[C]//International Conference on Electrical Engineering and Computer Science. Palembang: IEEE Press, 2017: 198-201.
|
| [7] |
Zhang Yanru, Han Zhu. Contract theory for wireless networks [M].[S.l.]: Springer International Publishing, 2017: 1-121.
|
| [8] |
Li Jun, Chu Shunfeng, Shu Feng, et al. Contract-based small-cell caching for data disseminations in ultra-dense cellular networks[J]. IEEE Transactions on Mobile Computing, 2019, 18(5): 1042-1053. DOI:10.1109/TMC.2018.2853746 |
| [9] |
Hamidouche K, Saad W, Debbah M. Breaking the economic barrier of caching in cellular networks: incentives and contracts[C]//IEEE Global Communications Conference. Washington: IEEE Press, 2016: 1-6.
|
| [10] |
Chu Shunfeng, Li Jun, Liu Tingting, et al. A contract-based incentive mechanism for data caching in ultra-dense small-cells networks[C]//IEEE Wireless Communications and Networking Conference. San Francisco: IEEE Press, 2017: 1-6.
|
| [11] |
Li Chenyu, Liu Jun, Ouyang Shuxin. Analysis and prediction of content popularity for online video service:a Youku case study[J]. China Communications, 2016, 13(12): 216-233. DOI:10.1109/CC.2016.7897546 |
| [12] |
Li Qiang, Zhang Yuanmei, Pandharipande A, et al. D2D-assisted caching on truncated Zipf distribution[J]. IEEE Access, 2019, 7: 13411-13421. DOI:10.1109/ACCESS.2019.2894837 |
| [13] |
Duan Lingjie, Gao Lin, Huang Jianwei. Cooperative spectrum sharing:a contract-based approach[J]. IEEE Transactions on Mobile Computing, 2014, 13(1): 174-187. |



