无线网络中的节点通常是移动的.这一动态特性为无线网络的路由设计带来了一定的挑战，如网络连通性难以维持、传输时延以及能量消耗的增加等.特别是对于稀疏移动网络，其在每一时隙的拓扑结构几乎都是不连通的，难以进行端到端的数据传输.因此，有必要在低节点密度的移动网络中研究网络的路由设计，即寻找一条低能耗的数据传输路径，并满足传输时延的约束.

静态网络中，低时延、低能耗的路由算法已有许多研究^[1-3].对于动态的随机移动网络，Sermpezis等^[4]分析了稀疏以及稠密移动网络中一类“传染病”路由的传输时延；张德千等^[5]基于学习理论提出了一种自适应路由算法.然而这类移动网络的路由设计并没有考虑移动节点的可预测性. Song等^[6]的研究结果表明，人类移动轨迹的预测可以到达93%以上.面向可预测的移动网络，Li等^[7]提出了低开销的启发式拓扑控制方法；Jiang等^[8]基于车辆移动轨迹设计了高效的多播机制；Yao等^[9]根据目的节点的移动方向预测出中继节点选择策略.这些研究的结果表明，利用网络拓扑的可预测性可以显著降低数据传输的开销.然而，这些工作要么要求网络拓扑是时时连通的，即非稀疏的网络场景，要么没有考虑端到端的传输时延要求.

面向低节点密度的移动网络，研究时延约束下能量高效的路径选择方法.将多个时隙的一系列静态网络拓扑建模为虚拟的空时图模型.在空间上，每一时隙的网络拓扑可能是不连通的；在时间上，由于节点的移动性，网络拓扑是动态变化的.重新定义端到端的路由问题为寻找一条低能耗的空时路径，并满足时延软约束.这里，时延软约束是指若给定时延约束内空时路径不存在，则将时延约束进行放松.仿真结果表明，该算法能够实现能量消耗与传输时延的折中.此外，放松时延约束，增加网络节点密度能够显著降低数据传输的能量消耗.

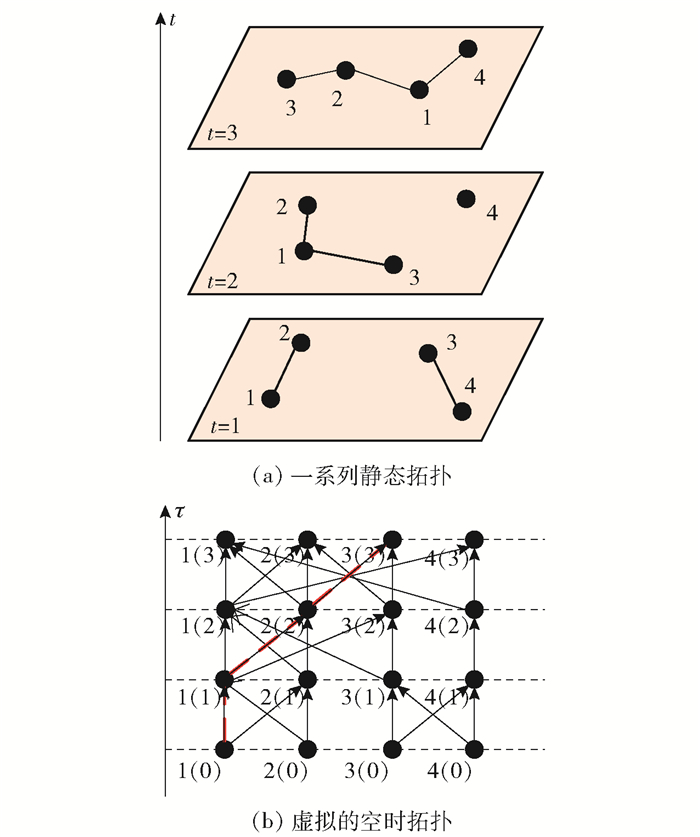
1 系统模型

将一个连续的时间段划分多个相等的时隙，分别为{1, 2, …, T}.当时隙较小时，每个时隙的网络拓扑可以近似视为一个静态图.采用无向图G^t(V, E^t)表示第t个时隙的网络拓扑，其中，V={1, 2, …, n}表示节点集合，(i, j)∈E^t表示无线链路，即在t时隙节点i和j可以相互通信.于是，一个时间段T内的动态网络可以由一系列静态拓扑构成，表示为{G^t|t=1, 2, …, T}，如图 1(a)所示.注意每个时隙的网络拓扑可能是不连通的.这里假设网络的拓扑变化是由节点的移动引起，且节点的移动轨迹是可预测的，即G^t是已知的.

将这一系列静态拓扑{G^t|t=1, 2, …, T}转换为一个虚拟的空时图^[7]，记作$\mathscr{G} $=($\mathscr{V} $, $\mathscr{E} $).其中，虚拟节点集$\mathscr{V} $={i(τ)|i=1, …, n, τ=0, 1, …, T}，虚拟节点i(τ)表示第τ时刻的节点i，图 1(b)为图 1(a)对应的空时图.空时图为有向图，既包含网络拓扑在每一时隙的无线链路连通信息，也包含由节点移动性引起的无线链路变化信息.在空时图模型中，$\overrightarrow {\left[{i\left({\tau - 1} \right), i\left(\tau \right)} \right]} $∈$\mathscr{E} $称为时间链路，表示节点i可以在第τ个时隙携带数据信息而不进行传输；$\overrightarrow {\left[{i\left({\tau - 1} \right), {j}\left(\tau \right)} \right]} $∈$\mathscr{E} $称为空间链路，表示节点i可以在第τ个时隙向节点j传输数据信息，即(i, j)∈E^τ.例如在图 1(b)中，虚线所标注的路径1(0)→1(1)→2(2)→3(3)包含一条时间链路以及2条空间链路(称该路径为空时路径).这一空时路径在图 1(a)中表示节点1传输数据信息至节点3采用如下方式：节点1在第1个时隙不进行数据传输；在第2个时隙节点1将数据传输至节点2；在第3个时隙节点2将数据转发至节点3.

2 问题描述

在虚拟的空时拓扑$\mathscr{G} $中，给定源节点s、目的节点d以及时延约束D.重新定义路由设计的目标是寻找一条满足时延约束D且具有最低能耗的空时路径Π连接s(0)以及d(τ)，其中0 < τ≤D.如果在时延约束D内，源、目的节点之间不存在空时路径，则放松该约束至D+1，称这一放松为时延的软约束.假设时间段T远大于时延约束D，使得源节点s与目的节点d在时间段T内存在一条空时路径.此外，假设在每一时隙内仅允许单跳的数据传输.

在新定义的路由问题中，如果时延约束D较小，可供选择的空时路径就越少，甚至不存在.例如在图 1(b)中，如果取D为2个时隙，节点1~3的空时路径仅有1(0)→1(1)→3(2)，而节点1~4之间则没有路径；如果取D为3个时隙，则节点1~3会增加一条可选路径，即1(0)→1(1)→2(2)→3(3)，节点1~4之间出现一条空时路径为1(0)→1(1)→1(2)→4(3).随着时延约束的增加，意味着有更多的空时路径可以进行选择.这也说明空时拓扑中的路由设计存在着能耗与时延的权衡.

数据信息在节点内维持以及在链路上传输均会产生一定的能量消耗，记为E(l)，如功率消耗、时延等.定义数据信息在一条路径Π上的传输能耗为该路径上所有链路的能耗之和，即${E_\mathit{\Pi }} = \sum\limits_{(i, j) \in \mathit{\Pi }} E (i, j)$.假设节点维持信息的能量消耗为固定值C₀，即时间链路的能耗为E₀.空间链路上的能量消耗定义收发节点之间距离的α次方，即

$ E\left( {i, j} \right) = \beta d{\left( {i, j} \right)^\alpha } $

其中：d(i, j)为收发节点之间的距离，α∈[2,4]为路径损耗因子，β为常数.事实上，链路的能量消耗可以更改为链路开销，根据实际场景包含更多的相关因素，如可用资源量、链路质量等.

3 路由算法

在传统静态网络拓扑中，为寻找源、目的节点之间的最低能耗路径，可以采用Dijkstra最短路算法.而在空时拓扑中，节点i(0), i(1), …, i(T)均为节点i，并且增加了时延的约束.基于Dijkstra最短路算法，笔者在空时网络拓扑上提出一种满足时延软约束的低能耗路由(ERDS，energy-efficient routing with delay soft-constraint)算法.算法步骤如下.

1) 根据时延约束D建立空时图网络$\mathscr{G} $，即只考虑前D个时隙的系列拓扑.确定每条链路l的能量消耗E(l).时间链路的能耗固定为E₀，空间链路的能耗为E(i, j)=βd(i, j)^α.若节点之间不存在链路，则定义E(l)=∞.

2) 初始化，记$\mathscr{R} $[j(τ)]为虚拟节点s(0)至j(τ)最短路径所包含的链路集合，$\mathscr{C} $[j(τ)]为对应的能耗值.对所有j=1, 2, …, n, τ=1, 2, …, D，令$\mathscr{R} $[j(τ)]=Ø，$\mathscr{C} $[j(τ)]=∞.再令i=s(0)，$\mathscr{C} $(i)=0.已访问节点集$\mathscr{N} $初始值为$\mathscr{N} $={i}.

3) 令temp=∞;

for j(τ)∈$\mathscr{V－N} $，记l=[i, j(τ)]

if $\mathscr{C} $(i)+E(l)≤$\mathscr{C} $[j(τ)]，then

$\mathscr{R} $[j(τ)]=$\mathscr{R} $(i)∪l，$\mathscr{C} $[j(τ)]=$\mathscr{C} $(i)+E(l);

end if

if $\mathscr{C} $[j(τ)]≤temp，then

 temp=$\mathscr{C} $[j(τ)]，i′=j(τ);

end if

end for

令i=i′，$\mathscr{N} $=$\mathscr{N} $∪{i}.

4) 重复步骤3)，直到d(D)∈$\mathscr{N} $.

5) 若$\mathscr{C} $(d(D))=∞，则令D=D+1，重复步骤1)~步骤4).

6) 重复步骤5)，直到$\mathscr{C} $[d(D)]≠∞.令$\mathscr{C} $[d(τ)]是$\mathscr{C} $[d(1)], $\mathscr{C} $[d(2)], …, $\mathscr{C} $[d(D)]中的最小者.于是，$\mathscr{R} $[d(τ)]即为源节点s与目的节点d之间满足软时延约束D的最低能耗空时路径，在该路径上传输数据的能耗为$\mathscr{C} $[d(τ)].

算法步骤2)~步骤4)主要是基于Dijkstra最短路算法.在步骤5)中，如果$\mathscr{C} $[d(D)]=∞，即无法得到源节点s与目的节点d之间的空时路径(见定理1)，则放松一个时隙的时延约束.由于空时拓扑中的节点数目为n(T+1)，所提算法在最差情况下的计算复杂度为O[n²(T+1)²].

定理1  给定时延约束D，算法执行至步骤5)，若$\mathscr{C} $[d(D)]=∞，则源节点s与目的节点d在时延约束D内不存在空时路径.

证明 采用反证法.假设源节点s与目的节点d在时延约束D内存在空时路径，不妨设该路径为s(0), …, d(τ)，其中τ∈{1, 2, …, D}，且有$\mathscr{C} $[d(τ)] < ∞.根据空时图模型，$\overrightarrow {[d\left(\tau \right), d\left({\tau + 1} \right)]} $∈$\mathscr{E} $为时间链路，其能耗为有限值E₀.于是，可以得到另一条空时路径s(0), …, d(τ), d(τ+1), …, d(D)，且$\mathscr{C} $[d(D)] < ∞.这与$\mathscr{C} $[d(D)]=∞矛盾.

4 仿真结果

在仿真中，初始时若干节点随机均匀地分布在500 m×500 m的平面区域内.从当前时隙至下一时隙，每一节点从当前位置以任意方向、从0~50 m每单位时隙选择任意速度移动至下一个位置.如果在节点移动过程中遇到边界，则反射至区域内.所有节点的覆盖范围为r_max =150 m，以生成每个时隙的网络拓扑.若2个节点在彼此的覆盖范围之内，两者可以相互通信.给定网络拓扑，随机选择源、目的节点对.其他仿真参数见表 1.

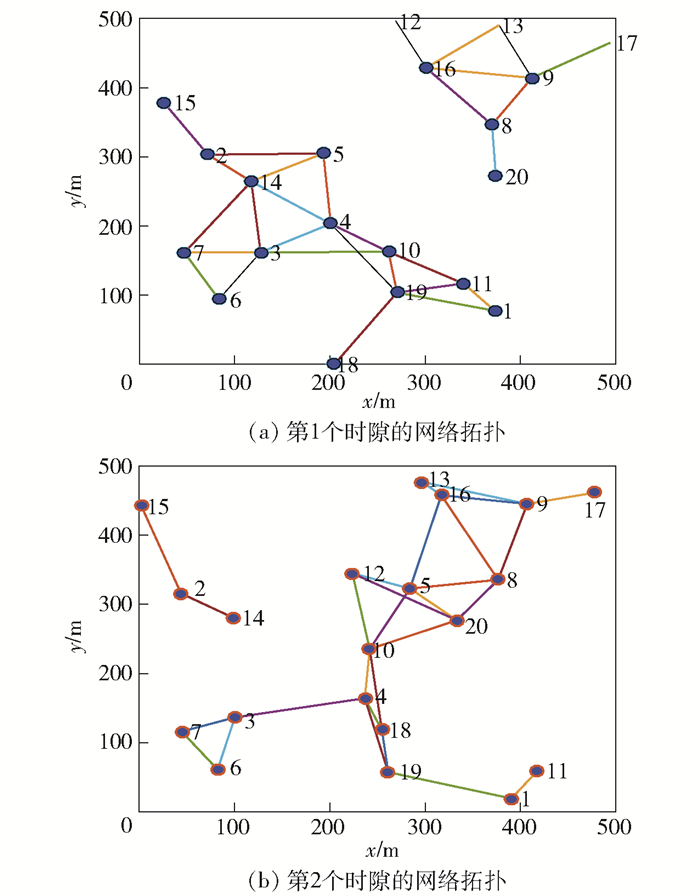
图 2所示为一个仿真实例用以刻画连续2个时隙网络拓扑的变化情况，其中节点数目n=20.可以看出，在稀疏的移动网络中，每一时隙的网络拓扑是高概率不连通的.因此，端到端的路由设计必须联合考虑多个时隙的网络拓扑.

ERDS算法与以下移动网络中两类常用的路由算法做比较：基于“传染病”的路由算法(epidemic-based routing)；基于距离的路由(distance-based routing).在基于“传染病”的路由算法中，携带信息的节点根据每个时隙的通信机会将信息“传染”至未携带信息的节点，直到目的节点获得信息.基于距离的路由算法的主要思想为当前的传输节点(包括源节点)根据其邻节点与目的节点的距离选择下一跳中继节点.

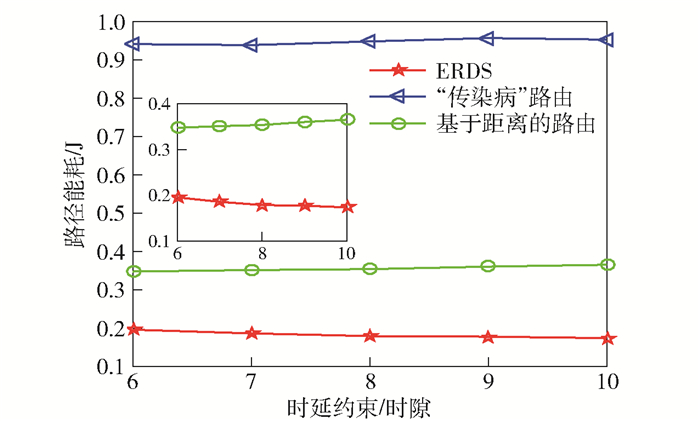
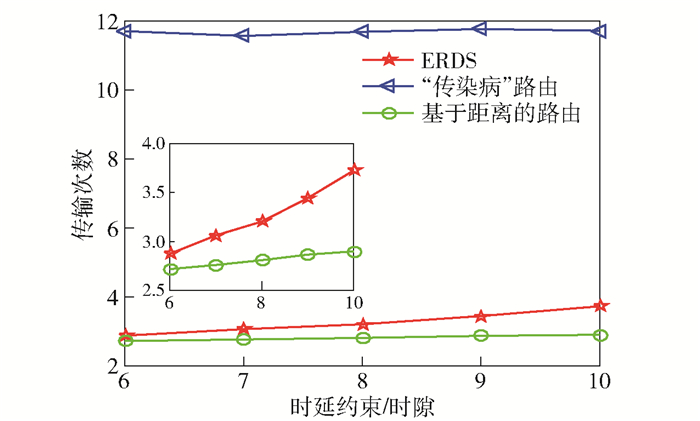
将时延约束从6变化至10个时隙，运行ERDS算法和比较算法，得到空时路径的最低能耗及其实际的传输次数(该路径包含的空间链路数目).空时路径的能量消耗以及传输次数与时延约束的关系分别如图 3和图 4所示，其中网络节点数目为20.仿真中的数据点是在3 000次空时拓扑中随机选择一对源、目的节点，取平均得到.从图 3可以看出，所提ERDS算法能够得到最低能耗的空时路径，而采用“传染病”路由传输数据信息显然会消耗过多的能量.随着时延约束的放松，ERDS算法能够产生能量更为高效的空时路径.这是因为节点之间可以选择较优的接触机会(较短的链路距离)进行数据信息传输，在接触机会较差时(较长的链路距离)携带数据信息不进行传输以节省能耗.从图 4可以看出，ERDS算法采用短链路进行信息传输，使得实际的传输次数随时延约束的放松而增加.这是因为能量随着距离指数次方衰减，故采用较短的链路进行信息传输可以降低能量消耗.

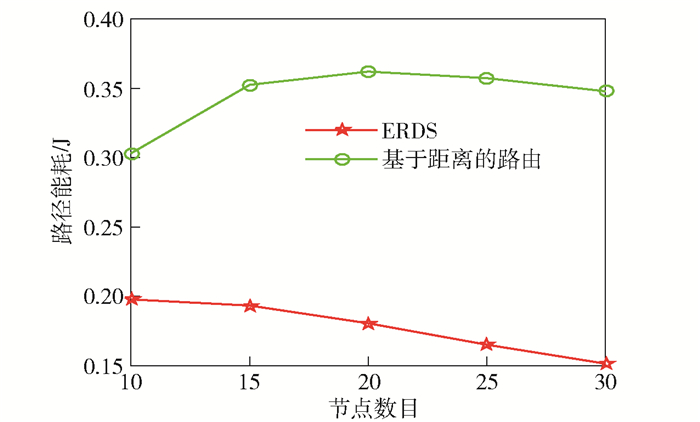
算法性能随节点数目的变化关系如图 5、图 6所示.其中，节点数目从10变化至30，时延约束为8个时隙.鉴于“传染病”路由算法的高能耗，此次仿真仅与基于距离的路由算法进行对比.可以看出，随着节点密度的增加，所提ERDS算法能够得到能量更为高效的空时路径.此外，在节点数目n=10与15时，2个算法所得到的空时路径包含几乎相同的空间链路数目.这是由于网络中节点数目过低，致使源、目的节点之间的空时路径数目较少.

从图 3、图 5中可以得出，放松时延约束、增加节点密度，ERDS算法能够提高端到端信息传输的能量高效性.从图 4、图 6中可以看出，实际的传输次数不高于时延约束的一半，说明在稀疏的移动网络中，节点更多的是携带信息不进行传输以等待更好的传输机会，即所提算法生成的空时路径中包含较多的时间链路.

5 结束语

能量消耗和时延是路由设计的2个重要考虑因素.为此，在稀疏的移动网络中提出了一种能量高效的路由算法，同时满足时延软约束.首先，将多个时隙的静态网络拓扑建模为虚拟的空时图模型；然后，重新定义端到端的路由问题为在时延软约束下寻找一条低能耗空时路径；最后，根据重新定义的路由问题，提出一种满足时延软约束的低能耗路由算法.仿真结果表明，该算法在能量高效性方面优于传统的路由算法，并且能够实现能量消耗与传输时延的权衡.特别地，当时延约束严厉时，数据传输应当珍惜每一次通信机会；随着时延约束的放松，数据传输可以选择较优的无线链路，以降低能耗.