2. 上海科技大学 创意与艺术学院, 上海 200135;
3. 中国科学院 上海微系统与信息技术研究所, 上海 200135
针对目前卫星移动通信系统中卫星组网能力欠缺等问题,在非地面网络基础上提出了一种基于虚拟卫星小区组网的多普勒频移估计和补偿算法.通过引入集中管理单元,移动终端能快速选择多普勒频移最小的卫星,同时根据传输时延和卫星星历对多普勒频移值进行估计、补偿、更新和再补偿.仿真结果表明,与传统算法相比,该算法有效降低了多普勒频移,提高了卫星通信链路的质量和接入成功率.
2. School of Creativity and Art, Shanghai University of Science and Technology, Shanghai 200135, China;
3. Shanghai Microsystems, Chinese Academy of Sciences Institute of Information Technology, Shanghai 200135, China
Aiming at problems such as lack of satellite networking capabilities in current satellite mobile communication systems, a Doppler frequency shift estimation and compensation algorithm based on virtual satellite cell networking is proposed on the basis of non-terrestrial networks. By introducing a centralized control unit, the user equipment can quickly select the satellite with the smallest Doppler frequency shift, and at the same time, the Doppler shift value is compensated, updated and re-compensated according to the transmission delay and the satellite ephemeris. Simulations show that, compared with the traditional algorithm, this algorithm effectively reduces the Doppler frequency shift, and improves the quality of satellite communication links and access success rate.
卫星通信是诸如飞机通信、海上船舶和偏远地区回程等场景中最好的(甚至是唯一的)通信方案[1].在大多数情况下,称为非地面网络(NTN,non-territory networking)的卫星通信网络,已被预测为第6代移动通信系统的重要组成部分,将与未来的地面网络无缝集成.但是,在非同步卫星移动通信系统中,由于卫星相对地面的高速移动性,接收端接收到的频率与波源的实际频率存在较大的多普勒频移,增加了接收端解调难度,使得通信性能降低.特别是近地球轨道卫星通信,由于其具有更低的轨道和更快的移动速度(存在非常短的有效覆盖时间窗口),而产生非常严重的多普勒频移效应.因而,在NTN移动通信中,如何使用户终端(UE,user equipment)快速、准确地接入通信卫星是个亟待解决的问题.
目前,多普勒频移估计与补偿的解决方案主要有3种:①直接使用几何分析法,计算通信卫星和地面终端的相对运动速度,进而计算出多普勒频移值[2-3];②使用卡尔曼滤波频移估算算法[4-5];③使用最大似然估计算法,对通信过程中的多普勒频移因子进行计算,并反馈到频率补偿模块,由频率补偿模块对发射信号频率进行预补偿,以达到收发双方频率同步的目的[6-7].这些多普勒频移的估算及补偿方法可降低多普勒频移值,提高通信质量,但也存在一定的问题,例如不适用于所有轨道类型,未考虑时延,而且多数研究主要集中在多普勒频移的估计算法上,很少关注UE和(或)卫星上的多普勒频移补偿、更新和再补偿程序的新技术.
针对上述问题,基于虚拟卫星小区(VSC,virtual satellite cell)组网的近地球轨道(LEO,low earth orbit)卫星通信过程提出的方法,适用于直连和非直连VSC中的集中控制单元(CCU,centralized control unit)的UE,在2种情况下分析了CCU与UE之间的交互方法和流程,利用VSC架构获取的信息来补偿NTN中非同步卫星通信场景下的多普勒频移.
1 算法详述 1.1 传统算法传统的频率补偿模型如图 1所示[8].随着卫星通信的广泛使用,越来越多的移动用户访问NTN,将导致两跳传输中的拥塞,增加传输错误,接收信号不准确,通信质量下降,进而导致多普勒频移补偿失败.然而,越来越多的卫星具备了许多先进的功能,可以通过卫星的星上处理(OBP,on board processing)[9]来估计和补偿多普勒频移.笔者提出了基于广播信道和上下行交互的2种方法,在VSC组网下实现UE快速选择最优多普勒频移的LEO卫星的解决方案,提高了更高的信号传输效率和准确性.

|
图 1 传统的多普勒频移补偿功能模块 |
提出的VSC组网包括CCU和分布式单元(DU,distributed unit),可以分别对应于3GPP NG-RAN(next generation-radio access network)架构中定义的gNB-CU(next generation noteb-control unit)和gNB-DU(next generation noteb-distributed unit)[10].增强了协议程序、功能和基于5G NG-RAN架构的接口,以支持NTN的要求. CCU和DU分离的结构对UE是透明的,并且与5G NG-RAN的架构兼容.部署在一个网元(NE,network element)的gNB-CU上的CCU负责管理来自特定区域中的多个DU的资源.
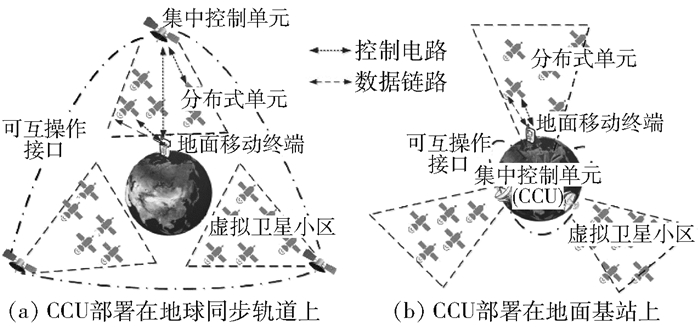
如图 2所示,VSC由集中控制单元CCU和多个分布式单元DU组成.地球同步轨道(GEO,geosynchronous orbit)卫星适合用作CCU[见图 2(a)],因为它对地面UE和基站是相对静态的,并且在所有类型的卫星中具有最小的多普勒频移效应.此外,GEO卫星具有更大的覆盖区域,有助于收集比LEO卫星更多的信息,因此可以管理更多的DU和UE.由于GEO卫星与UE之间的距离相对较长,因此不适合在GEO卫星上执行延迟敏感的业务.基站也适合作为CCU服务器[见图 2(b)].与GEO卫星相比,地面基站具有以下优点:延迟更短,空间上更接近5G核心网络,具有更好的可扩展性.然而,地面基站具有较小的空间覆盖范围,相比GEO卫星,需要CCU之间更频繁的互操作性.因此,可根据NTN要求,将CCU部署在GEO卫星或地面基站上.
|
图 2 非地面网络虚拟卫星小区网络架构的原理 |
当UE访问NTN时,需要选择合适的LEO,此时存在大量可能与之连接的LEO卫星,并且由于高多普勒频移效应,UE很难快速访问最佳LEO卫星和波束.因此,可使用CCU协助UE,以相对快的过程找到最佳的DU,并帮助补偿DU和UE之间的多普勒频移.
1) UE与GEO卫星直连的情况下的多普勒频移估计与补偿
UE将其自身的位置、速度和所需的服务质量(QoS,quality of service)需求信息(例如最大带宽,最小多普勒频移和GEO卫星与UE自身之间的最小时延)发送给为其服务的CCU,VSC中的所有DU也会周期性地将自己的星历信息发送给为其服务的CCU.由于CCU拥有UE和所有DUs的必要信息,所以可以选择满足UE的QoS要求的DUs及其波束. CCU还可以根据UE的移动速度、位置和DU的运动轨迹、位置和速度信息,估算所选DU和UE之间的多普勒频移值.基于CCU与UE,CCU和DU之间的传输时延对多普勒频移估计值进行补偿,然后将多普勒频移的初始估计值分别发送到DU和UE.在发现多普勒频移估计不准确的情况下,UE或DU还可以重新发送自己的位置、移动速度等信息给CCU,以请求对多普勒频移信息进行校正.然后,CCU将校正后的多普勒频移估计值反馈给UE或DU.
2) UE与GEO卫星不能直连的情况下的多普勒频移估计与补偿
对于一些UE无法实现和CCU双向通信的特殊情况,例如UE发射功率有限(无法与GEO卫星建立上行链路)或只有NTN链路而没有TN链路到基站,利用CCU的协助,将VSC覆盖的地理表面区域划分为不同的虚拟小区位置区域,每个虚拟小区位置区域被分配了一个唯一ID,其被称为虚拟小区位置区域地址(VCLID,virtual cell location area ID).对于特定CCU,VCLID信息是恒定的.然后将虚拟卫星小区子载波分组,每组子载波使用一个表映射到VCLID.区域子载波映射表对于特定CCU也是恒定的.子载波表的信息包括最佳DU的ID,其波束ID、接入码、频率、最佳的DU和虚拟小区位置区域的某个地理点之间的多普勒频移估计值.如果没有足够的子载波,可以定义由main-VCLID(MVCLID)和sub-VCLID(SVCLID)组成的2级VCLID. SVCLID是虚拟单元位置区域中的子区域的ID.这些信息由CCU定期广播,当UE接入虚拟卫星小区时,就能接收该信息,并且根据其地理位置信息,UE知道可能访问的最佳的LEO卫星以及与最佳LEO卫星相关的多普勒频移估计值.
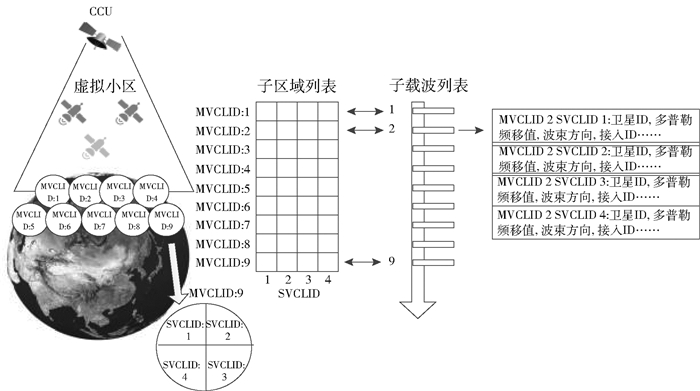
为便于理解,区域子载波映射的示例如图 3所示. CCU覆盖的地理区域划分为9个虚拟小区位置区域,并且每个虚拟小区位置区域被划分为4个子区域.然后,CCU的子载波被分成9组,每个子载波组携带4个子区域信息.因此,可以建立一个具有9×4的表格单元,并由CCU定期进行广播.
|
图 3 区域子载波的示例和子载波表的信息 |
目前,在空间通信系统中,最常用的估计方法是利用升交点赤金Ω、轨道倾角i、近地点俯角ω、轨道偏心率e、轨道半长轴a和过近地点的时刻tp六大轨道参数[11],确定其任何时刻的轨道运动规律,计算卫星的位置和速度.利用卫星仿真软件搭建仿真系统架构,得到基于ECI坐标系的卫星的位置[rs(x, y, z)]、速度[vs(Vx, Vy, Vz)]的矢量数据和UE的经纬高(L, B, h)数据,再根据坐标系之间的转换关系[12],得到LEO卫星和UE的相对位置和速度,进而由多普勒的原始定义推导出多普勒估计的表达式,以下为推导过程.
对于UEs, 利用经度纬度和高度可得到UEs的地理位置矢量:
| $ {\mathit{\boldsymbol{r}}_r} = \left[ {\begin{array}{*{20}{l}} {{x_r}}\\ {{y_r}}\\ {{z_r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {(N + h){\rm{cos}}B{\rm{cos}}L}\\ {(N + h){\rm{cos}}B{\rm{sin}}L}\\ {[N(1 - {e^2}) + h]{\rm{sin}}B} \end{array}} \right] $ | (1) |
其中:
| $ \begin{array}{*{20}{c}} {{\rm{d}}{s^2} = {\rm{d}}{x^2} + {\rm{d}}{y^2} + {\rm{d}}{z^2}}\\ {{\rm{d}}{s^2} = {{\left\| {\frac{{\partial x}}{{\partial B}}} \right\|}^2}{\rm{d}}{B^2} + {{\left\| {\frac{{\partial x}}{{\partial L}}} \right\|}^2}{\rm{d}}{L^2} + {{\left\| {\frac{{\partial x}}{{\partial h}}} \right\|}^2}{\rm{d}}{h^2}} \end{array} $ | (2) |
F(B)变换的雅克比矩阵为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{J}}_F}(\mathit{\boldsymbol{L}},\mathit{\boldsymbol{B}},\mathit{\boldsymbol{h}}) = \\ \left[ {\begin{array}{*{20}{c}} { - (N + h){\rm{cos}}B{\rm{sin}}L}&{ - (R + h){\rm{sin}}B{\rm{cos}}L}&{{\rm{cos}}B{\rm{cos}}L}\\ {(N + h){\rm{cos}}B{\rm{cos}}L}&{ - (R + h){\rm{sin}}B{\rm{sin}}L}&{{\rm{cos}}B{\rm{sin}}L}\\ 0&{(R + h){\rm{cos}}B}&{{\rm{sin}}B} \end{array}} \right] \end{array} $ | (3) |
其中
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{J}}_F}(\mathit{\boldsymbol{L}},\mathit{\boldsymbol{B}},\mathit{\boldsymbol{h}}) = \\ \left[ {\begin{array}{*{20}{c}} { - {\rm{sin}}L}&{{\rm{cos}}L}&0\\ {{\rm{cos}}L}&{{\rm{sin}}L}&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{ - {\rm{sin}}B}&{{\rm{sin}}B}\\ 0&{{\rm{cos}}B}&{{\rm{sin}}B} \end{array}} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {(N + h){\rm{cos}}B}&0&0\\ 0&{(R(B) + h)}&0\\ 0&0&1 \end{array}} \right] \end{array} $ | (4) |
其中
通过使用链规则,可以形成速度矢量:
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{x}}}}{{{\rm{d}}t}} = \frac{{\partial x}}{{\partial \mathit{\boldsymbol{L}}}}\frac{{{\rm{d}}\mathit{\boldsymbol{L}}}}{{{\rm{d}}t}} = {\mathit{\boldsymbol{J}}_F}(\mathit{\boldsymbol{L}},\mathit{\boldsymbol{B}},\mathit{\boldsymbol{h}})\left( {\begin{array}{*{20}{c}} {\dot L}\\ {\dot B}\\ {\dot h} \end{array}} \right) $ | (5) |
通过链式规则将UE速度
| $ \frac{{{\rm{d}}\lambda }}{{{\rm{d}}t}} = \frac{{{\rm{d}}\lambda }}{{{\rm{d}}s}}\frac{{{\rm{d}}s}}{{{\rm{d}}t}} $ | (6) |
式(2)中的线性元素现在可以用式(4)中给出的对角矩阵中元素的平方来表示,有
| $ {\rm{d}}{S^2} = {(N + h)^2}{\rm{co}}{{\rm{s}}^2}B{\rm{d}}{L^2} + {(R + h)^2}{\rm{d}}{B^2} + {\rm{d}}{h^2} $ | (7) |
| $ \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\gamma {\rm{sin}}\alpha {\rm{d}}s}\\ {{\rm{cos}}\gamma {\rm{cos}}\alpha {\rm{d}}s}\\ {{\rm{sin}}\gamma {\rm{d}}s} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {(N + h){\rm{cos}}B{\rm{d}}L}\\ {(R + h){\rm{d}}B}\\ {{\rm{d}}h} \end{array}} \right] $ | (8) |
所以UE的速度矢量
| $ {\kern 1pt} \frac{{{\rm{d}}\mathit{\boldsymbol{x}}}}{{{\rm{d}}t}} = \frac{{\partial x}}{{\partial \mathit{\boldsymbol{L}}}}\frac{{{\rm{d}}\mathit{\boldsymbol{L}}}}{{{\rm{d}}s}}\frac{{{\rm{d}}s}}{{{\rm{d}}t}} $ | (9) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\rm{d}}\mathit{\boldsymbol{x}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}s}}{{{\rm{d}}t}}\left( {\begin{array}{*{20}{c}} { - {\rm{sin}}L}&{{\rm{cos}}L}&0\\ {{\rm{cos}}L}&{{\rm{sin}}L}&0\\ 0&0&1 \end{array}} \right) \times \\ \left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&{ - {\rm{sin}}B}&{{\rm{cos}}B}\\ 0&{{\rm{cos}}B}&{{\rm{sin}}B} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\rm{cos}}\gamma {\rm{sin}}\alpha }\\ {{\rm{cos}}\gamma {\rm{cos}}\alpha }\\ {{\rm{sin}}\gamma } \end{array}} \right) \end{array} $ | (10) |
其中:标量
| $ {\mathit{\boldsymbol{r}} = {\mathit{\boldsymbol{r}}_s} - {\mathit{\boldsymbol{r}}_r}} $ | (11) |
| $ {\mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{v}}_s} - {\mathit{\boldsymbol{v}}_r}} $ | (12) |
由多普勒的原始定义得到多普勒频移fD为
| $ {f_D} = \frac{{|\mathit{\boldsymbol{v}}|f}}{c}\frac{{\mathit{\boldsymbol{rv}}}}{{|\mathit{\boldsymbol{r}}||\mathit{\boldsymbol{v}}|}} = \frac{{\mathit{\boldsymbol{frv}}}}{{c|\mathit{\boldsymbol{r}}|}} $ | (13) |
以5G网络、铱星系统、卫星仿真软件为参考平台搭建了实验仿真环境[14],通过卫星仿真软件建立星座模型,3D模型如图 4所示.其中,低轨卫星有275颗卫星,分布在25个轨道平面上,高度均在780 km,每个卫星轨道上均匀地分布着11颗卫星.每个轨道的升交点赤经参数如表 1所示,奇数和偶数轨道的平近点角参数如表 2所示.地球半径设为6 370 km,星间链路的载波频率fc设为20 GHz.

|
图 4 卫星仿真3D图 |
|
|
表 1 25个LEO卫星轨道参数分布 |
|
|
表 2 奇、偶数轨道卫星的平近点角参数 |
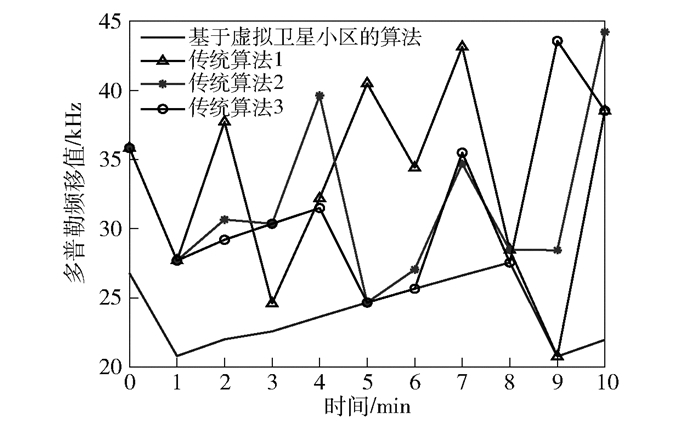
由仿真系统的设置参数以及式(13),可以计算出每个时刻UE和LEO卫星之间的多普勒频移变化值(这里取绝对值).由于铱星系统的可视时间最大为670 s,所以在卫星运行24 h内,选取连续运行10 min作为仿真时间参数.如图 5所示,横轴表示时间,纵轴表示10 min内移动通信过程中不同算法产生的多普勒频移值随着时间变化的情况.
|
图 5 LEO卫星和UE之间的多普勒频移值的对比 |
由图 5可以看到,所提出的算法在10 min内产生的多普勒频移最大值不超过27 kHz,而多种传统方法(获取某一时刻与UE建立通信关系的卫星的方法与所提算法不同,而估算多普勒频移值方法相同的方法,可参考引言部分描述)下产生的多普勒频移值是在23~44 kHz范围内波动.因此,说明了所提出的算法缩短了UE和最佳LEO卫星的连接过程的时间,减少了移动通信过程中产生的多普勒频移值,提高了通信质量和通信效率.
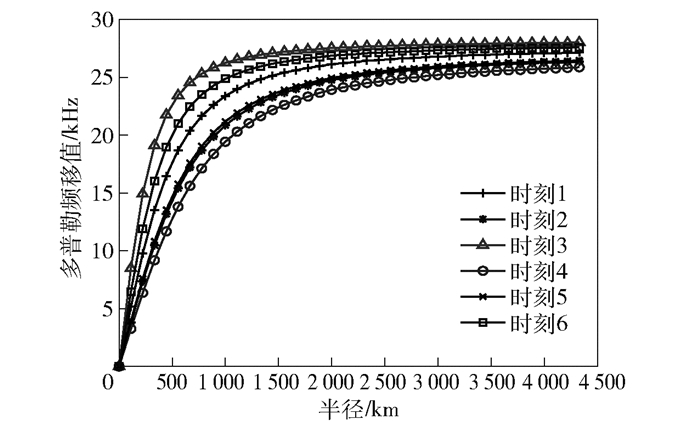
2.2.2 多普勒频移与地理位置区域的关系针对“一些UE无法直连CCU的特殊情况,将VSC覆盖的地理表面区域划分为不同的虚拟小区位置区域”,在提出算法的基础上,图 6显示了需要划分出虚拟小区位置区域的范围大小和多普勒频移值的关系.
|
图 6 地理位置区域的范围与多普勒频移的关系 |
首先,选定某时刻上空的LEO卫星,将LEO卫星星下点区域取为UE的参考基点(仰角略大于90°),半径设为100 km,向外依次增大区域范围半径;然后,基于上述推导,仿真估算出该时刻LEO卫星分别与不同范围内的UE之间产生的多普勒频移值,并分析出区域范围的差异和多普勒频移值之间的关系.如图 6所示,横轴表示不同区域范围的半径,纵轴表示在多个不同时刻条件下不同地理区域范围内的UE和LEO卫星之间产生的多普勒频移值.由图 6可知,多普勒频移为15 kHz时支持的最大覆盖范围是500 km;当覆盖范围是1 000 km时,多普勒频移值大约是22 kHz左右,即区域范围越大,多普勒效应越严重.
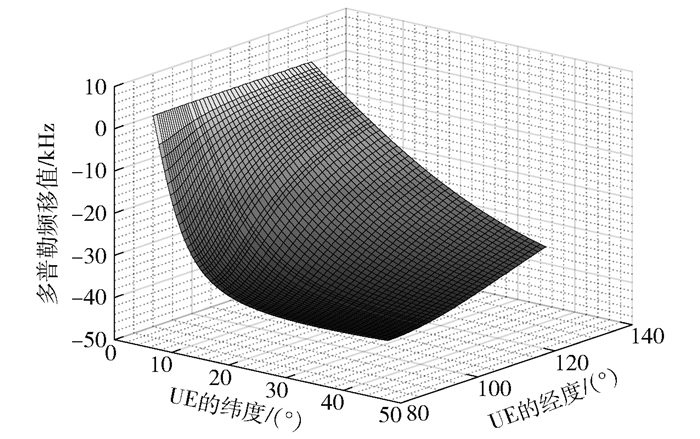
对于不同经纬度的UE,在移动通信过程中,LEO卫星和UE之间产生的多普勒频移值也不同,如图 7所示.以赤道上空的LEO卫星作为参考点,UE均匀地分布在0°~40°N,90°E~140°E范围内.如图 7所示,在一定经纬度范围内,随着UE经纬度的增加,通信过程产生的多普勒频移值也会增加,且赤道附近的UE和LEO卫星之间产生的多普勒频移值最小.
|
图 7 UE的经纬度与多普勒频移值的关系 |
针对不同能力的终端,笔者提出了基于广播信道和上下行交互的2种方法,在VSC组网下实现UE快速选择最优多普勒频移的LEO卫星的解决方案,具有改进的功效和准确性.与传统方法相比,实时星上处理的工作集中在CCU上完成,通过CCU进行测量、校正,补偿了系统中的多普勒频偏,满足了动态连续跟踪需要.由于UE在不同地理区域位置的多普勒频移值不同,所以,为解决不同地理位置对多普勒频移的影响也提供了仿真参考,一定程度上扩大了所提方案的应用范围.
| [1] |
Minoli D. Innovations in satellite communications and satellite technology: the industry implications of DVB-S2X high throughput satellites ultra HD M2M and IP, hoboken, NJ[M].[S.l.]: Wiley, 2015: 2387-2396.
|
| [2] |
Hu Cheng, Tian Ye, Zeng Tao, et al. Adaptive secondary range compression algorithm in geosynchronous SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(4): 1397-1413. DOI:10.1109/JSTARS.2015.2477317 |
| [3] |
Jayaprakasam S, Ma X, Choi J W, et al. Robust beam-tracking for wave mobile communications[J]. IEEE Communications Letters, 2017, 21(12): 2654-2657. DOI:10.1109/LCOMM.2017.2748938 |
| [4] |
Koivisto M, Costa M, Werner J, et al. Joint device positioning and clock synchronization in 5G ultra-dense networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(5): 2866-2881. DOI:10.1109/TWC.2017.2669963 |
| [5] |
Chan A C, Srinivasan V J, Lam E Y. Maximum likelihood doppler frequency estimation under decorrelation noise for quantifying flow in optical coherence tomography[J]. IEEE Transactions on Medical Imaging, 2014, 33(6): 1313-1323. DOI:10.1109/TMI.2014.2309986 |
| [6] |
Linty N, Presti L. Doppler frequency estimation in GNSS receivers based on double FFT[J]. IEEE Transactions on Vehicular Technology, 2016, 65(2): 509-524. DOI:10.1109/TVT.2015.2398196 |
| [7] |
Zhao Yongsheng, Zhao Congjun, Zhao Chuang. Joint delay-Doppler estimation for passive bistatic radar with direct-path interference using MCMC method[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 130-136. |
| [8] |
Liu Jianfeng, Wang Hongsong, Li Yun. Compensation of Doppler frequency satellite mobile communication[J]. Journal of Chongqing University of Posts & Telecommunications (Natural Science Edition), 2014, 26(3): 1-8. |
| [9] |
Lee Y, Choi J P. Performance evaluation of high-frequency mobile satellite communications[J]. IEEE Access, 2019, 7(1): 49077-49087. |
| [10] |
3GPP 38401. NG-RAN architecture description[S].[S.l.]: 3GPP, 2018.
|
| [11] |
Dai Cuiqin, Zheng Guimin, Chen Qianbin. Satellite constellation design with multi-objective genetic algorithm for regional terrestrial satellite network[J]. China Communications, 2018, 15(8): 1-10. |
| [12] |
Richard W M. Satellite orbits in digital communications with emphasis on data modems: theory, analysis, design, simulation, testing, and applications[M].[S.l.]: Wiley, 2017: 1120-1128.
|
| [13] |
Barry Matin. B.1.ECEF velocity vector[EB/OL]. Lodon: Barry Matin, 2014[2019-06-27]. http://www.aqqa.org/MH370/models/ECEF_velocity_vector.pdf.
|
| [14] |
Zhang Liangliang, Ma Debao, Niu Chaoyang. Simulation and analysis of ACB'S photometric signature based on STK[J]. Proceeding of SPIE-the International Society for Optical Engineering, 2010, 7658(835): 56278-56332. |


