针对时间反演多址系统中信道的相关性会导致多用户干扰的问题,为了消除用户间干扰,降低计算复杂度,提出基于最小均方误差的3条对角线矩阵分解的低复杂度近似算法.首先提取检测矩阵(Gram-N)中包含主对角线的3条对角线矩阵;然后将3对角线矩阵分成2个2对角线矩阵;再利用2对角线矩阵求逆规律,分别求出这2个2对角线矩阵的逆,由此得出3对角线矩阵的逆;最后,根据诺依曼级数近似,用3对角线矩阵这个稀疏矩阵的逆来逼近Gram-N的逆.仿真结果表明,该算法在误码率和频谱效率方面具有明显的性能优势,并且具有较低的复杂度,在复杂度较低时可获得近乎最优的性能增益.
Aiming at solving the problem of multi-user interference caused by channel correlation in time reversal division multiple access system, eliminating inter-use interference and reducing computational complexity, a low complexity approximation algorithm of matrix decomposition of tridiagonal matrices based on minimum mean square error is proposed.Firstly, the tridiagonal matrix that include the main diagonal line in the detection matrix(Gram-N) is extracted, and the tridiagonal matrix into two double diagonal lines matrices is divided.Then, by using the inverse rule of double diagonal lines matrix, the inverse of these two double diagonal lines matrices is obtained, the inverse of the tridiagonal lines matrix is applied in the algorithm.Finally, according to the Neumann series approximation, the goal of approximating Gram-N's inverse is realized by using the inverse of tridiagonal matrix.Simulations show that the proposed algorithm has obvious performance advantages in terms of bit error rate, spectral efficiency, and complexity.The algorithm can obtain a near-optimal performance gain when the complexity is low.
随着互联网络的发展,越来越多的无线设备需要接入无线网络,传统多址技术难以满足日益增多的用户需求.时间反演多址(TRDMA,time reversal division multiple access)因其良好的时空聚焦特性而被认为是一种有利于构建低复杂度、高利用率的绿色通信的空分多址技术[1].
TRDMA技术根据信道冲激响应之间的独立性来区分用户[2].然而,在实际的通信中,信道彼此之间并不是处处独立的.信道之间的相关性会导致用户之间的干扰,也会导致信道容量的损耗.因此有必要消除用户间干扰. TRDMA系统消除干扰的算法可以引用码分多址(CDMA,code division multiple access)系统里的检测算法[3].经典的线性检测算法有迫零算法(ZF,zero forcing)和最小均方误差算法(MMSE,minimum mean square error). MMSE检测算法在收发天线比值较大时被证明能够取得趋近最优的检测效果,然而MMSE检测算法要对大规模的矩阵进行求逆计算,复杂度很高,不适合在实际中应用[4].
为了减小求逆矩阵的复杂度,中外学者相继提出了基于MMSE准则的低复杂度检测算法,主要有矩阵近似求逆、迭代求解线性方程、基于梯度搜索的3类算法. ①迭代求解线性方程算法:Tang等[5]利用高斯迭代求解线性方程,避免了大矩阵的复杂求逆运算,且需要的迭代次数较少. ②梯度搜索:Jin等[6]基于共轭梯度,给了一种低复杂度检测方法. ③近似求逆算法:Tang等[7]提到的基于MMSE的主对角牛顿迭代法(DBNI,diagonal based on newton iteration),通过牛顿迭代计算主对角线矩阵的逆,利用诺依曼级数逼近大矩阵的逆,复杂度减小了.曹海燕等[8]提出基于MMSE的2对角线的诺依曼级数(TNS,two-diagonal neumann series)检测方法,将大矩阵分成2对角线阵和空心阵,取诺依曼级数前两项来近似求逆结果,以此降低复杂度,且检测性能较好.
基于此,采用第1类近似求逆方法,在TRDMA系统里,提出基于MMSE的3对角矩阵分解的诺依曼级数(TDNS,tridiagonal-matrix decomposition Neumann series)检测方法,降低了复杂度,检测性能逼近MMSE.
1 系统模型系统为多输入多输出(MIMO,multiple-user single input multiple output)上行链路,包括一个有W根接收天线的基站,N个有单发送天线的用户,W>>N.信道是瑞利衰落信道. 图 1所示为加入TDNS算法的TRDMA系统框图.
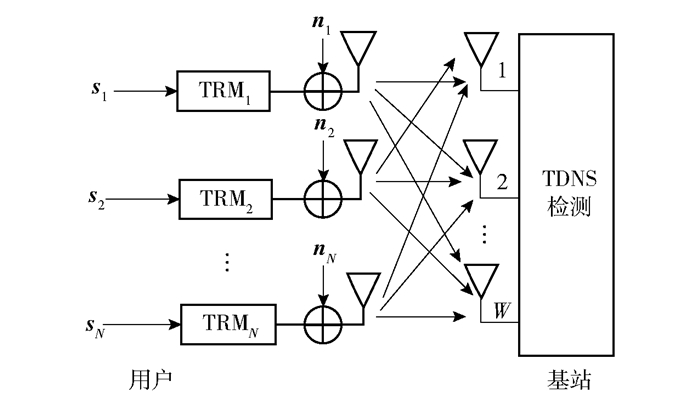
|
图 1 系统框图 |
假设N个用户同时发送信号,s=[s1, s2, …, sN]T为所有用户同时发送的信号组成的N×1维向量,用户n∈{1, 2, …, N}和基站端第i∈{1, 2, …, W}根接收天线之间的信道增益为
| $ h_i^{(n)}(t) = \sum\limits_{k = 0}^{l - 1} {{\alpha _{i,k}}} \delta (t - {\tau _{i,k}}) $ | (1) |
其中:l为多径总数;k表示第k条多径,k∈{0, 1, …, l-1},k=0为第0条多径,物理意义上为第1条多径,多径数从0开始记数,便于后续计算;αi, k为第i根接收天线第k条多径的幅度;τi, k为第i根接收天线第k条多径的时延. hi(n)(t)在时域上离散化为矩阵hi(n).
TRDMA的通信过程分为3步.
1) 用户发射信号前的准备阶段:基站发射探测信号.
2) 位于用户附近的时间反演镜(TRM,time reversal mirror)阵列接收探测信号并对其在时域进行反转,形成gi(n).
3) TRM发射反演后的信号,此时为正式通信过程,信号会聚焦在基站.在公式上体现为,信道hi(n)变为hi(n)*gi(n),*为卷积,gi(n)由hi(n)经TR和归一化后得到,是hi(n)经过时间反演后的增益向量[1].
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{g}}_i^{(n)} = \frac{{\mathit{\boldsymbol{\bar h}}_i^{(n)}[l - 1 - k]}}{{\sqrt {\sum\limits_{i = 1}^N E [{{\left\| {\mathit{\boldsymbol{h}}_i^{(n)}} \right\|}^2}]} }} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\mathit{\boldsymbol{\bar h}}_i^{(n)}[l - 1 - k]}}{{\sqrt {E\left[ {N\sum\limits_{k = 0}^{l - 1} | \mathit{\boldsymbol{h}}_i^{(n)}[k]{|^2}} \right]} }}} \end{array} $ | (2) |
其中:‖·‖表示Frobenius范数,h表示h的共轭.第n个用户与第i根天线之间的信道经TRM后演变为
| $ \begin{array}{l} \mathit{\boldsymbol{H}}_i^{(n)} = (\mathit{\boldsymbol{h}}_i^{(n)}*\mathit{\boldsymbol{g}}_i^{(n)})[k] = \sum\limits_{p = 0}^{l - 1} {\mathit{\boldsymbol{h}}_i^{(n)}} [p]\mathit{\boldsymbol{g}}_i^{(n)}[k - p] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\limits_{p = 0}^{l - 1} {\mathit{\boldsymbol{h}}_i^{(n)}} [p]\mathit{\boldsymbol{\bar h}}_i^{(n)}[l - 1 - k + p]}}{{\sqrt {E[N\sum\limits_{k = 0}^{l - 1} | \mathit{\boldsymbol{h}}_i^{(n)}[k]{|^2}]} }} \end{array} $ | (3) |
其中:∀k, p∈{0, 1, …, 2l-2}. k=l-1时对应自相关函数的最大功率中心峰值,有
| $ (\mathit{\boldsymbol{h}}_i^{(n)}*\mathit{\boldsymbol{g}}_i^{(n)})[l - 1] = \frac{{\sum\limits_{k = 0}^{l - 1} | \mathit{\boldsymbol{h}}_i^{(n)}[k]{|^2}}}{{\sqrt {E\left[ {N\sum\limits_{k = 0}^{l - 1} | \mathit{\boldsymbol{h}}_i^{(n)}[k]{|^2}} \right]} }} $ | (4) |
假设信道状态信息(CSI,channel state information)已知,s发出后经TRM向量gi(n)调制,基站端接收到的W×1维的信号记为Y,每根接收天线接收到的信号是所有用户发送的信号(N个用户,每个用户l条多径)及其反演信号叠加后形成的,记为Yi,1≤i≤W,Yi可以表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_i} = \mathit{\boldsymbol{Hs}} + \mathit{\boldsymbol{n}} = }\\ {\sum\limits_{n = 1}^N {\mathit{\boldsymbol{h}}_i^{(n)}} *\mathit{\boldsymbol{g}}_i^{(n)}\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{n}} = }\\ {\sum\limits_{n = 1}^N {(\mathit{\boldsymbol{h}}_i^{(n)}*\mathit{\boldsymbol{g}}_i^{(n)})} [l - 1]\mathit{\boldsymbol{s}} + } \end{array} $ | (5a) |
| $ {\sum\limits_{\begin{array}{*{20}{c}} {k = 0}\\ {k \ne l - 1} \end{array}}^{2l - 2} {\sum\limits_{n = 1}^N {(\mathit{\boldsymbol{h}}_i^{(n)}*\mathit{\boldsymbol{g}}_i^{(n)})} } [k]\mathit{\boldsymbol{s}} + } $ | (5b) |
| $ {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^W {\sum\limits_{k = 0}^{2l - 2} {\sum\limits_{n = 1}^N {(\mathit{\boldsymbol{h}}_i^{(n)}*\mathit{\boldsymbol{g}}_j^{(n)})} } } [k]\mathit{\boldsymbol{s}} + } $ | (5c) |
| $ {\sum\limits_{k = 0}^{2l - 2} {{\mathit{\boldsymbol{n}}_i}} [k]} $ | (5d) |
其中:∀i, j∈{1, 2, …, W},
式(5)是将基站端每根接收天线接收到的信号Yi进一步展开的形式,式(5a)部分是接收到的主要期望信号,信道为该信号的hi(n)*gi(n),为时间反演自相关函数,此时k=l-1是最大功率中心峰值;式(5b)部分是用户间的干扰,k=l-1这条多径是当前用户期望信号自相关函数聚焦峰值处,k≠l-1的多径处的信号相当于旁瓣信号,其他用户对当前用户的干扰;式(5c)部分是基站端接收天线之间干扰,第j, j≠i根接收天线对第i根接收天线的干扰,这部分信号的信道是hi(n)*gj(n),为时间反演互相关函数,物理意义是该信号的信道卷积了相邻信道的时间反演参数;式(5d)部分是噪声.
将W×1维列向量Y送入TDNS执行多用户检测,基站收到经过检测以后的信号
1) G-1矩阵诺依曼级数近似
对G矩阵诺依曼级数展开,有
| $ {\mathit{\boldsymbol{G}}^{ - 1}} = \mathop \sum \limits_{n = 0}^\infty {[{\mathit{\boldsymbol{P}}^{ - 1}}(\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{G}})]^n}{\mathit{\boldsymbol{P}}^{ - 1}} $ | (6) |
其中P为可逆矩阵,并满足
| $ \mathop {{\rm{lim}}}\limits_{n \to \infty } {(\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{G}})^n} = 0 $ | (7) |
通过取式(6)前L项来近似G-1,有
| $ {\mathit{\boldsymbol{\tilde G}}^{ - 1}} = \mathop \sum \limits_{n = 0}^{L - 1} {[{\mathit{\boldsymbol{P}}^{ - 1}}(\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{G}})]^n}{\mathit{\boldsymbol{P}}^{ - 1}} $ | (8) |
2) G矩阵3对角线稀疏化提取
提取G的3条对角线作为稀疏化处理,以降低复杂度,记为
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{G_{11}}}&{{G_{12}}}&0& \cdots & \cdots &0\\ {{G_{21}}}&{{G_{22}}}&{{G_{23}}}& \cdots & \cdots &0\\ \vdots & \vdots & \vdots & \cdots & \cdots & \vdots \\ 0&0&0& \ddots & \ddots &{{G_{(N - 1)N}}}\\ 0&0&0& \cdots &{{G_{N(N - 1)}}}&{{G_{NN}}} \end{array}} \right] $ | (9) |
3) 3对角线矩阵P求逆
通过求P-1,再进行诺依曼级数近似求得G-1. G抽取P后的空心矩阵记为K,有G=P+K.为了方便计算,用字母代替矩阵中的元素.通过Thomas算法[9],将P分成2个2对角线的矩阵,分别为Z和X,有
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}&{{b_1}}&0& \cdots &0\\ {{c_2}}&{{a_2}}&{{b_2}}& \cdots &0\\ 0&{{c_3}}&{{a_3}}& \ddots &0\\ \vdots & \vdots & \ddots & \ddots &{{b_{N - 1}}}\\ 0& \cdots & \cdots &{{c_N}}&{{a_N}} \end{array}} \right] = \mathit{\boldsymbol{ZX}} = \\ \left[ {\begin{array}{*{20}{c}} 1&0&0& \cdots & \cdots &0\\ {{d_2}}&1&0& \cdots & \cdots &0\\ 0&{{d_3}}&1& \cdots & \cdots &0\\ \vdots & \vdots & \ddots & \ddots & \vdots &{}\\ 0&0& \cdots & \cdots &{{d_N}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{e_1}}&{{b_1}}&0& \cdots & \cdots &0\\ 0&{{e_2}}&{{b_2}}&0& \cdots &0\\ 0&0&{{e_3}}&{{b_3}}& \cdots &0\\ 0&0&0& \ddots & \ddots &{{b_{N - 1}}}\\ 0& \cdots & \cdots & \cdots & \ddots &{{e_N}} \end{array}} \right] \end{array} $ | (10) |
其中:e1=a1,dN=cN/eN-1,eN=aN-dN/bN-1. a、b、c、d、e没有具体含义,为了表达计算规律而用字母代替. P中3条对角线元素已知,即b1~bN-1、a1~aN、c2~cN的值是已知的. X中b1~bN-1的值就是P中b1~bN-1的值,因此可算出Z、X中每一项元素.通过这种方法,将3对角线矩阵P分解成2个2对角线矩阵Z和X,且可求出Z和X.
由(10)式可得
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}^{ - 1}} = {\mathit{\boldsymbol{X}}^{ - 1}}{\mathit{\boldsymbol{Z}}^{ - 1}} = \\ {\left[ {\begin{array}{*{20}{c}} {{e_1}}&{{b_1}}&0& \cdots & \cdots &0\\ 0&{{e_2}}&{{b_2}}&0& \cdots &0\\ 0&0& \ddots & \ddots & \cdots &0\\ \vdots & \vdots & \ddots & \ddots & \cdots &{{b_{N - 1}}}\\ 0&0& \cdots & \cdots & \cdots &{{e_N}} \end{array}} \right]^{ - 1}} \times \\ {\left( {{{\left[ {\begin{array}{*{20}{c}} 1&{{d_2}}&0& \cdots & \cdots &0\\ 0&1&{{d_3}}&0& \cdots &0\\ 0&0&1&{{d_4}}& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \ddots &{{d_N}}\\ 0&0&0& \cdots & \cdots &1 \end{array}} \right]}^{\rm{T}}}} \right)^{ - 1}} \end{array} $ | (11) |
要求得P-1,要分别求出X-1和Z-1.首先对X做等价变换[6],有
| $ \begin{array}{l} \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&{\frac{{{b_1}}}{{{e_2}}}}&0& \cdots & \cdots &0\\ 0&1&{\frac{{{b_2}}}{{{e_3}}}}& \cdots & \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \ddots &{\frac{{{b_{N - 1}}}}{{{e_N}}}}\\ 0&0&0& \cdots & \cdots &1 \end{array}} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{e_1}}&0&0& \cdots &0\\ 0&{{e_2}}&0& \cdots &0\\ 0&0&{{e_3}}& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&0& \cdots &{{e_N}} \end{array}} \right] \end{array} $ | (12) |
假设N为奇数,若N为偶数,最后一列每一项符号相反.对于2条对角线的矩阵
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 1&{{\beta _0}}&0& \cdots & \cdots &0\\ 0&1&{{\beta _1}}& \cdots & \cdots &0\\ \vdots & \vdots & \ddots & \ddots &{}& \vdots \\ 0&0& \cdots & \cdots & \cdots &1 \end{array}} \right] $ | (13) |
其逆B-1有如下规律[8]:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{B}}^{ - 1}} = \\ \left[ {\begin{array}{*{20}{c}} 1&{ - {\beta _0}}&{{\beta _0}{\beta _1}}&{ - {\beta _0}{\beta _1}{\beta _2}}& \cdots &{ - {\beta _0}{\beta _1}{\beta _2} \cdots {\beta _{N - 1}}}\\ 0&1&{ - {\beta _1}}&{{\beta _1}{\beta _2}}& \cdots &{{\beta _1}{\beta _2} \cdots {\beta _{N - 1}}}\\ \vdots & \vdots & \vdots & \ddots & \ddots & \vdots \\ 0&0&0& \cdots & \cdots &1 \end{array}} \right] \end{array} $ | (14) |
由B-1的求导规律,可推导出X-1和Z-1.
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{X}}^{ - 1}} = \\ \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{e_1}}}}&{ - \frac{{{b_1}}}{{{e_1}{e_2}}}}&{\frac{{{b_1}{b_2}}}{{{e_1}{e_2}{e_3}}}}&{ - \frac{{{b_1}{b_2}{b_3}}}{{{e_1}{e_2}{e_3}{e_4}}}}& \cdots &{\frac{{{b_1}{b_2}{b_3} \cdots {b_{N - 1}}}}{{{e_1}{e_2}{e_3}{e_4} \cdots {e_N}}}}\\ 0&{\frac{1}{{{e_2}}}}&{ - \frac{{{b_2}}}{{{e_2}{e_3}}}}&{\frac{{{b_2}{b_3}}}{{{e_2}{e_3}{e_4}}}}& \cdots &{ - \frac{{{b_2}{b_3} \cdots {b_{N - 1}}}}{{{e_2}{e_3}{e_4} \cdots {e_N}}}}\\ \vdots & \vdots & \vdots & \ddots & \ddots & \vdots \\ 0&0&0& \cdots &0&{\frac{1}{{{e_N}}}} \end{array}} \right] \end{array} $ | (15) |
| $ {\mathit{\boldsymbol{Z}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} 1&0&0& \cdots &0\\ { - {d_2}}&1&0& \cdots &0\\ {{d_2}{d_3}}&{ - {d_3}}&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{d_2}{d_3}{d_4} \cdots {d_N}}&{ - {d_3}{d_4} \cdots {d_N}}&{{d_4} \cdots {d_N}}& \cdots &1 \end{array}} \right] $ | (16) |
通过P-1=X-1Z-1,可得出P-1,由于P-1矩阵每项元素过大,将P的每项元素用符号代替,再详细给出每项元素的表达式.
| $ {\mathit{\boldsymbol{P}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{\alpha _{11}}}&{{\alpha _{12}}}&{{\alpha _{13}}}& \cdots &{{\alpha _{1N}}}\\ {{\alpha _{21}}}&{{\alpha _{22}}}&{{\alpha _{23}}}& \cdots &{{\alpha _{2N}}}\\ {{\alpha _{31}}}&{{\alpha _{32}}}&{{\alpha _{33}}}& \cdots &{{\alpha _{3N}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{\alpha _{N1}}}&{{\alpha _{N2}}}&{{\alpha _{N3}}}& \cdots &{{\alpha _{NN}}} \end{array}} \right] $ | (17) |
其中:在P-1第1行中,除了第1列和第N列元素,有一个通用规律,因此把第1列和第N列元素单独列出,其余列用通式表达.第1行第1列的值为
| $ {\alpha _{{\rm{11}}}} = \frac{{\prod\limits_{i = 2}^N {{e_i}} + {b_1}{d_2}\prod\limits_{i = 3}^N {{e_i}} + \cdots + \prod\limits_{i = 1}^{N - 1} {{b_i}} \prod\limits_{i = 2}^N {{d_i}} }}{{\prod\limits_{i = 1}^N {{e_i}} }} $ | (18) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{1j}} = \\ \frac{1}{{\prod\limits_{i = 1}^N {{e_i}} }}\left\{ {{{( - 1)}^{j - 1}}\left[ {\prod\limits_{i = 1}^{j - 1} {{b_i}} \prod\limits_{j = i + 1}^N {{e_i}} + \prod\limits_{i = 1}^j {{b_i}} {d_{j + 1}}\prod\limits_{i = j + 2}^N {{e_i}} + } \right.} \right.\\ \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \prod\limits_{i = 1}^{j + 1} {{b_i}} \prod\limits_{i = j + 1}^{j + 2} {{d_i}} \prod\limits_{i = j + 3}^N {{e_i}} + \cdots + \prod\limits_{i = 1}^{N - 1} {{b_i}} \prod\limits_{i = j + 1}^N {{d_i}} } \right]} \right\}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2 \le j \le N - 1 \end{array} $ | (19) |
第1行第N列为
| $ {\alpha _{1N}} = \frac{{\prod\limits_{i = 1}^{N - 1} {{b_i}} }}{{\prod\limits_{i = 1}^N {{e_i}} }} $ | (20) |
第2行除去第1、2列和最后一列,都有通用的规律,因此第2行第1、2列以及最后一列单独列出,其余列用通式表达.每行最后一列通式之间也有规律,i的起始值为当前行数.
第2行第1列为
| $ \begin{array}{l} {\alpha _{21}} = \frac{1}{{\prod\limits_{i = 2}^N {{e_i}} }}\left( { - {d_2}\prod\limits_{i = 3}^N {{e_i}} - {b_2}{d_2}{d_3}\prod\limits_{i = 4}^N {{e_i}} - } \right.\\ \begin{array}{*{20}{c}} {{b_2}{b_3}{d_2}{d_3}{d_4}\prod\limits_{i = 5}^N {{e_i}} - }\\ {\left. {{b_2}{b_3}{b_4}{d_2}{d_3}{d_4}{d_5}\prod\limits_{i = 6}^N {{e_i}} - \cdots - \prod\limits_{i = 2}^{N - 1} {{b_i}} \prod\limits_{i = 2}^N {{d_i}} } \right)} \end{array} \end{array} $ | (21) |
第2行第2列为
| $ \begin{array}{l} {\alpha _{22}} = \frac{1}{{\prod\limits_{i = 2}^N {{e_i}} }}\left( {\prod\limits_{i = 3}^N {{e_i}} + {b_2}{d_3}\prod\limits_{i = 4}^N {{e_i}} + {b_2}{b_3}{d_3}{d_4}\prod\limits_{i = 5}^N {{e_i}} + } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_2}{b_3}{b_4}{d_3}{d_4}{d_5}\prod\limits_{i = 6}^N {{e_i}} + \cdots + \prod\limits_{i = 2}^{N - 1} {{b_i}} \prod\limits_{i = 3}^N {{d_i}} } \right) \end{array} $ | (22) |
从第2行第3列开始到第2行第N-1列,有如下规律
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{2j}} = \\ \frac{1}{{\prod\limits_{i = 2}^N {{e_i}} }}\left\{ {{{( - 1)}^j}\left[ {\prod\limits_{i = 2}^{j - 1} {{b_i}} \prod\limits_{i = j + 1}^N {{e_i}} + \prod\limits_{i = 2}^j {{b_i}} {d_{j + 1}}\prod\limits_{i = j + 2}^N {{e_i}} + } \right.} \right.\\ \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \prod\limits_{i = 2}^{j + 1} {{b_i}} \prod\limits_{i = j + 1}^{j + 2} {{d_i}} \prod\limits_{i = j + 3}^N {{e_i}} + \cdots + \prod\limits_{i = 2}^{N - 1} {{b_i}} \prod\limits_{i = j + 1}^N {{d_i}} } \right]} \right\}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3 \le j \le N - 1 \end{array} $ | (23) |
第2行第N列为
| $ {\alpha _{2N}} = \frac{{ - \prod\limits_{i = 2}^{N - 1} {{b_i}} }}{{\prod\limits_{i = 2}^N {{e_i}} }} $ | (24) |
中间行的规律类似,每行前面无规律的列数逐行递增,最后一列元素i的起始值随着行数递增.中间行通式之间有如下规律:含有bi的元素,递乘i的起始值随着行数递增.中间行规律省略,以下列出最后一行元素.
第N行第1列到第N列有共同规律,用通式表达第N行第1列到第N列的规律,有
| $ {\alpha _{Nj}} = \frac{{{{( - 1)}^{j - 1}}\prod\limits_{i = j + 1}^N {{d_i}} }}{{{e_N}}},1 \le j \le N $ | (25) |
求出P-1后,通过诺依曼级数近似得出G-1.将P-1代入式(8)可得前L项的G-1为
| $ {\mathit{\boldsymbol{\tilde G}}^{ - 1}} = \sum\limits_{n = 0}^{L - 1} {{{( - {\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{K}})}^n}} {\mathit{\boldsymbol{P}}^{ - 1}} $ | (26) |
取L=2时,式(26)为
| $ {\mathit{\boldsymbol{\tilde G}}^{ - 1}} = {\mathit{\boldsymbol{P}}^{ - 1}} - {\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{P}}^{ - 1}} $ | (27) |
式(27)中,
以计算复杂度为指标来分析复杂度问题.工作是降低G-1矩阵复杂度,因此可分析G-1.
|
|
表 1 计算复杂度的对比 |
平均误比特率(BER,bit error rate)为[10]
| $ {\bar P_{\rm{e}}} = {\left( {\frac{{1 - \mu }}{2}} \right)^N}\sum\limits_{i = 0}^{N - 1} {\left( {\begin{array}{*{20}{c}} {N - 1 - i}\\ i \end{array}} \right)} {\left( {\frac{{1 + \mu }}{2}} \right)^i} $ | (28) |
其中:
系统的频谱效率为
| $ R = \sum\limits_{n = 1}^N {\rm{l}} {\rm{b}}(1 + f) $ | (29) |
f为信干噪比(SINR,signal to interference and noise ratio),由文献[1]可得平均SINR为
| $ f = E\left[ {\frac{{{P_{{\rm{Sig}}}}}}{{{P_{{\rm{ISI}}}} + {P_{{\rm{IUI}}}} + {\sigma ^2}}}} \right] \approx \frac{{E[{P_{{\rm{Sig}}}}]}}{{E[{P_{{\rm{ISI}}}}] + E[{P_{{\rm{IUI}}}}] + {\sigma ^2}}} $ | (30) |
| $ E[{P_{{\rm{Sig}}}}] = \frac{{1 + {{\rm{e}}^{ - l{T_S}/{\sigma _T}}}}}{{1 + {{\rm{e}}^{ - {T_S}/{\sigma _T}}}}} + N\frac{{1 - {{\rm{e}}^{ - l{T_S}/{\sigma _T}}}}}{{1 - {{\rm{e}}^{ - {T_S}/{\sigma _T}}}}} $ | (31) |
| $ E[{P_{{\rm{IUI}}}}] = \frac{{2{{\rm{e}}^{ - {T_S}/{\sigma _T}}}(1 - {{\rm{e}}^{ - (L - 1){T_S}/{\sigma _T}}})}}{{(1 - {{\rm{e}}^{ - {T_S}/{\sigma _T}}})(1 + {{\rm{e}}^{ - {T_S}/{\sigma _T}}})}} $ | (32) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E[{P_{{\rm{IAI}}}}] = \\ (W - 1)\frac{{(1 + {{\rm{e}}^{ - \frac{{2l{T_S}}}{{{\sigma _T}}}}})(1 + {{\rm{e}}^{ - \frac{{{T_S}}}{{{\sigma _T}}}}}) - 2{{\rm{e}}^{ - \frac{{(l + 1){T_S}}}{{{\sigma _T}}}}}(1 + {{\rm{e}}^{ - \frac{{{T_S}}}{{{\sigma _T}}}}})}}{{(1 - {{\rm{e}}^{ - \frac{{2{T_S}}}{{\sigma T}}}})(1 - {{\rm{e}}^{ - \frac{{l{T_S}}}{{\sigma T}}}})}} \end{array} $ | (33) |
在仿真中,信道为多径瑞利衰落信道,信道增益服从均值为0、方差为e-kTS/σT的循环对称复高斯(CSCG,cyclically symmetric complex gaussian)随机变量,0≤k≤l.采用16-QAM调制方式.设信道带宽B=500 MHz,采样周期TS=1/B=200 ns,均方根延迟扩展σT=100/B,时间反演多径数l=16[1].以下仿真都是在时间反演系统中.基站端分别配置32、64、128根接收天线,均设置8个单天线用户.
图 2所示为MMSE和TDNS在L=2、3、4的BER性能对比. MMSE作为精确求逆算法,作为参考的标准.随着天线数增大,TDNS越逼近MMSE. W=128时,L=2、3、4时BER与MMSE的BER基本重合.
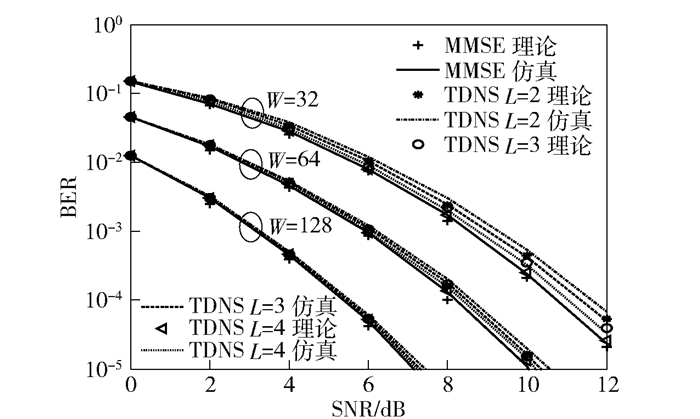
|
图 2 L=2、3、4时TDNS检测算法BER对比 |
图 3所示为MMSE、本文TDNS、文献[7]DBNI、文献[8]TNS在L=2时的BER性能对比. MMSE作为精确求逆算法,作为参考的标准值.在W=32、64、128时,TDNS算法的BER比文献[7]和文献[8]的更低,且W=32、64时,性能有更明显提高.
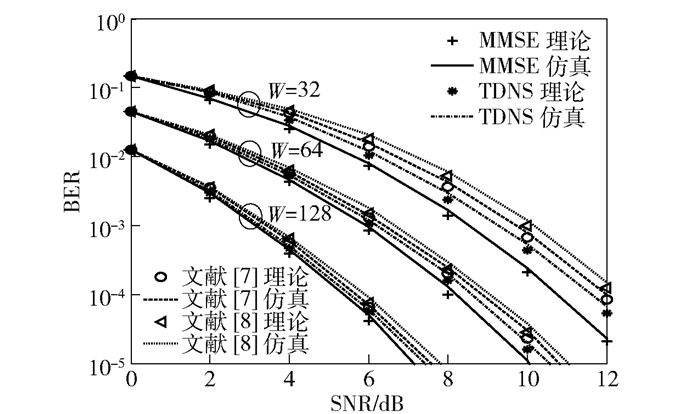
|
图 3 L=2时4种算法BER对比 |
图 4所示为文献[7]DBNI在L=3时与TDNS、文献[8]TNS在L=2时的BER.随着W成倍数的增大,3种算法的BER越相近. W=128时,TDNS的BER与MMSE基本稳合,L=3时DBNI的BER依然差于L=2时的TDNS,W越小,差距越明显.

|
图 4 L=3时DBNI与L=2时TDNS、TNS的BER对比 |
天线设置为基站端64根接收天线,8个单天线用户. 图 5所示为MMSE、TDNS在L=2、3、4时的频谱效率与SNR的对比.频谱效率随着L增大而增高,但增益不大.频谱效率随着SNR增大而增高,在SNR大时,频谱效率明显得到提升.
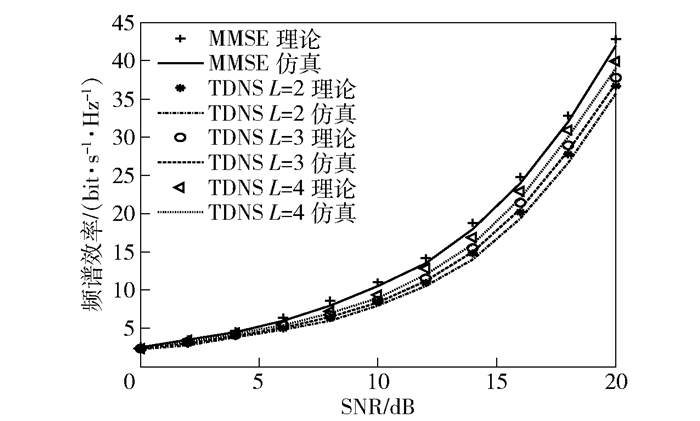
|
图 5 W=64,L=2、3、4时TDNS频谱效率对比 |
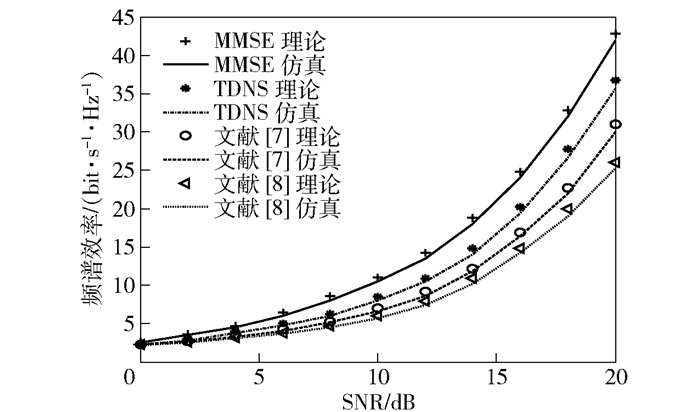
图 6所示为MMSE、TDNS、文献[7]、文献[8]在L=2时的频谱效率与SNR的对比.在低SNR下,频谱效率随SNR的增大趋近对数关系.在高SNR下,频谱效率随SNR的增大呈线性关系.取L=2时,3种低复杂度算法中TDNS性能最好.
|
图 6 W=64,L=2时4种算法频谱效率对比 |
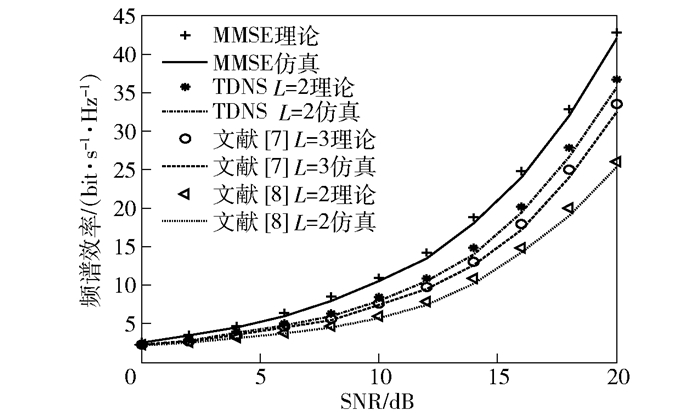
图 7所示为文献[7]在L=3时与TDNS、文献[8]TNS在L=2时的频谱效率.结合图 6、图 7,L=3时DBNI的频谱效率高于L=2时DBNI的频谱效率,但依然低于L=2时的TDNS.
|
图 7 L=3时的DBNI与L=2时的TDNS、TNS的频谱效率对比 |
下面给出系统性能和复杂度的折中分析:综合以上计算复杂度、BER以及频谱效率的分析,可以得出,L取相同项数时,TDNS是3种算法中性能最好的. TDNS取L=2更佳,此时复杂度为O(N2),天线配置方面应满足W>>N.
4 结束语针对TRDMA上行链路系统中用户间干扰导致的BER高以及频谱效率低的问题,提出了基于3对角矩阵分解的低复杂度检测算法.通过提取3条对角线元素以及Neumann级数展开,对Gram-N矩阵稀疏化处理,避免了MMSE复杂矩阵的求逆运算,在Neumann级数选取L=2时将复杂度从O(N3)降为O(N2).通过理论分析和仿真结果对比,证明了所提算法理论的正确性,该算法可以有效解决TRDMA系统上行链中多用户间干扰的问题.
| [1] |
Han Feng, Yang Yuhan, Wang Beibei, et al. Time-reversal division multiple access over multi-path channels[J]. IEEE Transactions on Communications, 2012, 60(7): 1953-1965. DOI:10.1109/TCOMM.2012.051012.110531 |
| [2] |
Cheng Jie, Wang Wenqin, Chen Hui, et al. Temporal focusing effects of time-reversal frequency diverse array antenna[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(9): 1858-1862. DOI:10.1109/LAWP.2019.2931457 |
| [3] |
Tao Liu, Zhu Shihua, Gao Feifei. A simplified MMSE equalizer for distributed TR-STBC systems with multiple CFOs[J]. IEEE Communications Letters, 2012, 16(8): 1300-1303. DOI:10.1109/LCOMM.2012.052112.120410 |
| [4] |
Jin Fangli, Liu Qiufeng, Liu Hao, et al. A low complexity signal detection scheme based on improved newton iteration for massive MIMO systems[J]. IEEE Communications Letters, 2019, 23(4): 748-751. DOI:10.1109/LCOMM.2019.2897798 |
| [5] |
Tang Zihan, Wang Jun, Song Jian, et al. A low-complexity detection algorithm for uplink NOMA system based on gaussian approximation[C]//2017 IEEE Wireless Communications and Networking Conference(WCNC). San Francisco: IEEE Press, 2017: 1-6.
|
| [6] |
Jin Jiejun, Xue Ye, Ueng Y L, et al. A split pre-conditioned conjugate gradient method for massive MIMO detection[C]//2017 IEEE International Workshop on Signal Processing Systems(SiPS). Lorient: IEEE Press, 2017: 1-6.
|
| [7] |
Tang Chuan, Liu Cang, Yuan Luechao, et al. High precision low complexity matrix inversion based on newton iteration for data detection in the massive MIMO[J]. IEEE Communications Letters, 2016, 20(3): 490-493. DOI:10.1109/LCOMM.2015.2514281 |
| [8] |
曹海燕, 杨敬畏, 方昕. 大规模MIMO系统中基于二对角矩阵分解的低复杂度检测算法[J]. 电子与信息学报, 2018, 4(2): 416-420. Cao Haiyan, Yang Jingwei, Fang Xin. Low complexity detection algorithm based on two-diagonal matrix decomposition in massive MIMO systems[J]. Journal of Electronics & Information Technology, 2018, 4(2): 416-420. |
| [9] |
Murphy B J. Solving tridiagonal systems on a GPU[C]//20th Annual International Conference on High Performance Computing. Bangalore: IEEE Press, 2013: 159-168.
|
| [10] |
朱江, 王雁, 杨甜. 无线多径信道中基于时间反演的物理层安全传输机制[J]. 物理学报, 2018, 67(5): 1-12. Zhu Jiang, Wang Yan, Yang Tian. Secure transmission mechanism based on time reversal over wireless multipath channels[J]. Acta Physica Sinica, 2018, 67(5): 1-12. |



