针对超可靠低时延通信的收发设备能量受限和超可靠性要求的特点,将多天线技术应用于无线能量捕获的短包传输系统,研究了多用户多天线无线能量传输(MIMO-WET)系统中短包传输的块错误概率性能.首先利用每个用户的信噪比累积分布函数和高斯函数近似的方法,推导出块错误概率的近似闭合表达式;然后对无线能量传输阶段中的时隙数和无线信息传输(WIT)阶段中的功率分配系数因子进行联合优化,实现总块错误概率的最小化.仿真结果验证了所推导的块错误概率闭合表达式的正确性,并根据仿真数据得到:在给定信息传输的块长度和天线数量条件下,WET和WIT所用时隙数存在最优值.
Aiming at the characteristics of ultra-reliable low-latency communication transceiver equipment with limited energy and ultra-reliability requirements, the multi-antenna technology is applied to the short-packet transmission system of wireless energy harvesting and the packet error probability (PEP) performance of multiuser multi-antenna-wireless energy transmission (MIMO-WET) system with short-packet transmission is studied accordingly. Firstly, an approximate closed-form expression of the packet error probability is obtained by utilizing the cumulative distribution function of the signal-to-noise ratio for each user and the Gaussian function approximation method.Then the number of channel uses in the wireless energy transmission phase and the power allocation factors in the wireless information transmission (WIT) phase are jointly optimized for minimizing the sum-PEP of all users.Simulations validate the correctness of the closed expression of the packet error probability.It is shown that there are optimum numbers of channels uses for WET and WIT for given packet length of information transmission and the number of antennas.
超可靠低时延通信(URLLC,ultra-reliable and low-latency communication)需要在时延受限的条件下准确地传递信息[1],故可采用短数据包进行传输;由于数据包长度有限,不再使用香农定理的最大互信息算法[2].最大可达速率(MAR, maximal achievable rate)不但与信道分布有关,而且也与块错误概率(PEP, packet error probability)有关[3];同时,在URLLC下,收发设备大多是能量受限的,需要采用能量捕获的方式获取能量,以供数据传输.多天线技术能够利用空间资源实现复用增益,提高短数据包传输系统的MAR以及能量传输效率,进而降低传输时延;同时也可以实现分集增益,从而降低系统的PEP.
Khan和Lopez等[3-4]推导了点对点的单天线无线能量传输(WET,wireless energy transmission)系统中短包传输的MAR和PEP;Lopez等[5]认为能量捕获URLLC系统的时延其与系统的PEP成反比;Yang等[6]研究了能量捕获受限条件下系统的MAR性能,认为MAR与PEP和信道散度有关.由此可以看出,PEP直接影响短数据包传输的MAR,从而进一步影响其传输时延;同时捕获能量的多少直接影响发射功率的大小,进而影响PEP和MAR.所以,PEP能够表征短数据包传输系统的可靠性、有效性和能量捕获效率,并影响整个系统的时延.然而,以上研究都是针对理想状态的点对点通信系统,未考虑多设备连接场景. Gu等[7]分别在时分多址接入和迫零波束成形情景下研究了多用户短包传输系统的PEP,并分别对块长度分配和功率分配系数进行优化,使系统的总PEP最小,但未考虑能量捕获问题. Hu等[8]研究了协作多终端短包传输系统的PEP,但由于能量开销较大,无法使用WET为设备提供能量以供数据传输.由以上研究发现,多用户MIMO-WET系统中短包传输的PEP性能尚无研究.
针对此问题,在多用户MIMO-WET短包传输系统中,为能量发射器(ET,energy transmitter)和源节点配置多根天线,利用源节点捕获到的能量进行信息发送;根据源节点与用户的空间分布和迫零波束成形方法得到每个用户的信噪比累积分布函数,并利用高斯函数近似的方法,推导出每个用户的块错误概率的近似闭合表达式.利用基于块坐标下降(BCD,the block coordinate descent)和凹凸过程(CCCP,concave-convex procedure)的迭代算法,对WET阶段中的时隙数和无线信息传输(WIT,wireless information transmission)阶段中的功率分配系数因子进行联合优化,实现总块错误概率的最小化.理论分析结果表明,块错误概率与信息传输的块长度、功率分配系数成反比.仿真结果验证了所推导的块错误概率闭合表达式的正确性.根据仿真数据可知,在给定信息传输的块长度和天线数量条件下,WET和WIT所用时隙数存在最优值.
1 系统模型将多天线技术应用到无线能量捕获短包传输系统中,系统由ET、源节点S和K个用户组成,如图 1所示.由于节点能量受限,K个用户都配备单天线,并分布于不同的位置,分别用U1, U2, …, UK表示;ET的天线数量为NET,源节点的天线数量为N.假设能量捕获节点使用存储然后传输协议进行无线通信,整个过程分为WET阶段和WIT阶段.首先,源节点S在m个时隙中通过ET发出的射频(RF,radio frequency)信号进行能量收集,并存入电池中,即WET阶段;然后,源节点利用收集的能量,通过n个时隙与目的节点进行信息传输, 即WIT阶段.假设信道为准静态衰落信道,并且在每一个传输块中其衰落系数都固定不变.另外,假设ET到S具有完美的信道状态信息(CSI,channel state information),每个时隙的持续时间为Tc.
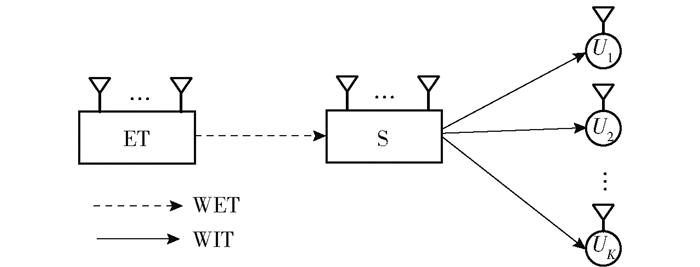
|
图 1 系统模型 |
首先考虑在ET处的能量波束成形,假设在ET处一共有d个能量波束,1≤d≤NET. ET处传输的能量信号为
| $ \mathit{\boldsymbol{S}} = E(\mathit{\boldsymbol{x}}{\mathit{\boldsymbol{x}}^{\rm{H}}}) = \sum\limits_{i = 1}^d {{\mathit{\boldsymbol{\omega }}_i}} \mathit{\boldsymbol{\omega }}_i^{\rm{H}} \ge 0 $ | (1) |
源节点S捕获的能量为
| $ Q = \eta LE({\left\| {\mathit{\boldsymbol{Hx}}} \right\|^2}) = \eta L{\rm{tr}} (\mathit{\boldsymbol{GS}}) $ | (2) |
其中:η为能量捕获效率;L为块长度;H为ET到S之间的MIMO信道矩阵,G
由文献[1]得知,设一个连续时间信号的近似持续时间为t,近似带宽为B,则数据包长度为:L≈Bt.因此,L≈BmTc.式(2)可以写为
| $ Q \approx \eta Bm{T_{\rm{c}}} {\rm{tr}} (\mathit{\boldsymbol{GS}}) $ | (3) |
其中:S
源节点S利用捕获的能量与K个用户进行信息传输.此阶段采用迫零波束成形方案. K个用户同时与S进行通信,数据包长度为M, M≈BnTc,功率分配系数为βk. PS为源节点S的传输功率,有
| $ {P_{\rm{S}}} = \frac{Q}{{n{T_{\rm{c}}}}} = \frac{{\eta Bm {\rm{tr}} (\mathit{\boldsymbol{GS}})}}{n} $ | (4) |
最大传输功率为
| $ P_{\rm{S}}^* = \frac{{{Q^*}}}{{n{T_{\rm{c}}}}} = \frac{{\eta BmP{\lambda _1}}}{n} $ | (5) |
用户k的接收信号为
| $ {y_k} = \sqrt {{P_{\rm{S}}}} \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{h}}_k} + {n_k} $ | (6) |
其中:hk~CN(0N, ΩkIN), k=1, 2, …, K为S与Uk之间的N×1信道矢量;Ωk为S与Uk的平均信道功率增益;xk为源节点S给用户k传输的信息;nk~CN(0,σk2)为加性高斯白噪声;
| $ {\gamma _k} = \frac{{{P_{\rm{S}}}{\beta _k}|\mathit{\boldsymbol{h}}_k^\dagger {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_k}{\mathit{\boldsymbol{h}}_k}|}}{{\sigma _k^2}} $ | (7) |
其中:Θk=IN-Hk(Hk†Hk)-1Hk†;Hk=[h1, h2, …, hK].
1.3 性能分析源节点S以固定的速率r进行信息传输,系统的性能主要由块错误概率和时延来描述.假设υk是S为用户k传输的信息比特数,则传输速率为rk=υk/M.
类似文献[5]的时延定义,假设从WET阶段到WIT阶段完成整个过程中,系统的时延为δ,δ*为满足给定错误概率的最小时延.
| $ \delta = (m + n){T_{\rm{c}}} $ | (8) |
对于系统总块错误概率,首先需要求出用户k错误概率的近似表达式.假设εk为用户k的错误概率,当n>100时,在准静态衰落信道中,εk可以近似为
| $ {\varepsilon _k} \approx E\left\{ {Q\left[ {\frac{{C({\gamma _k}) - {r_k}}}{{\sqrt {V({\gamma _k})/M} }}} \right]} \right\} $ | (9) |
其中:C(γk)=lb(1+γk)为由香农定理得到的信道容量;V(γk)=[1-1/(1+γk)2](lbe)2为信道散度;
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Q\left( {\frac{{C({\gamma _k}) - {r_k}}}{{\sqrt {V({\gamma _k})/M} }}} \right) \approx \varOmega ({\gamma _k}) = \\ \left\{ {\begin{array}{*{20}{l}} {1,\quad {\gamma _k} \le {\zeta _k}}\\ {\frac{1}{2} - {v_k}\sqrt M ({\gamma _k} - {\theta _k}),\quad {\xi _k} \le {\gamma _k} \le {\zeta _k}}\\ {0,\quad {\gamma _k} \ge {\xi _k}} \end{array}} \right. \end{array} $ | (10) |
其中:
式(7)已经得出Uk的SNR,通过文献[11]得到用户k SNR的累积分布函数(CDF,cumulative distribution function)
| $ {F_{{\gamma _k}}}(x) = 1 - \sum\limits_{i = 0}^{N - K} {\frac{{{{\left( {\frac{{\sigma _k^2}}{{{P_{\rm{S}}}{\beta _k}{\varOmega _k}}}x} \right)}^i}}}{{i!}}} {\rm{exp}}\left( { - \frac{{\sigma _k^2}}{{{P_S}{\beta _k}{\varOmega _k}}}x} \right) $ | (11) |
因此,其概率密度函数(PDF,probability density function)为
| $ \begin{array}{*{20}{c}} {{f_{{\gamma _k}}}(x) = \sum\limits_{i = 0}^{N - K} {\frac{{{\psi ^{i + 1}}{x^i}}}{{i!}}} {\rm{exp}}( - \psi x) - }\\ {\sum\limits_{i = 1}^{N - K} {\frac{{{\psi ^i}{x^{i - 1}}}}{{(i - 1)!}}} {\rm{exp}}( - \psi x)} \end{array} $ | (12) |
其中
| $ {\varepsilon _k} = \int_0^\infty {{f_{{\gamma _k}}}} (x)Q\left( {\frac{{C(x) - {r_k}}}{{\sqrt {V(x)/M} }}} \right){\rm{d}}x $ | (13) |
把式(9)代入式(13)中,得
| $ \begin{array}{*{20}{c}} {{\varepsilon _k} \approx \int_0^\infty {{f_{{\gamma _k}}}} (x)\varOmega ({\gamma _k}){\rm{d}}x = }\\ {\int_0^{{\zeta _k}} {{f_{{\gamma _k}}}} (x){\rm{d}}x + {\omega _1}\int_{{\zeta _k}}^{{\xi _k}} {{f_{{\gamma _k}}}} (x){\rm{d}}x - }\\ {{\omega _2}\int_{{\zeta _k}}^{{\xi _k}} x {f_{{\gamma _k}}}(x){\rm{d}}x} \end{array} $ | (14) |
其中:
为进一步推导,首先要计算
| $ \int_0^u {{x^n}} {\rm{exp}}( - \mu x){\rm{d}}x = {\mu ^{ - n - 1}}\Gamma (n + 1,\mu u) $ |
其中Γ(·, ·)为低阶不完全Gamma函数.因此
| $ \begin{array}{*{20}{c}} {\int_{{u_1}} {{x^n}} {\rm{exp}}( - \mu x){\rm{d}}x = }\\ {\int_0^{{u_2}} {{x^n}} {\rm{exp}}( - \mu x){\rm{d}}x - \int_0^{{u_1}} {{x^n}} {\rm{exp}}( - \mu x){\rm{d}}x = }\\ {{\mu ^{ - n - 1}}[\Gamma (n + 1,\mu {u_2}) - \Gamma (n + 1,\mu {u_1})]} \end{array} $ | (15) |
然后把用户k SNR的PDF和以上关于∫xnexp(-μx)dx的计算代入式(14)中进行化简整理,得到用户k的块错误概率近似表达式,有
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{\varepsilon _k} \approx \sum\limits_{i = 0}^{N - K} {\frac{{\Gamma (i + 1,\psi {\zeta _k})}}{{i!}}} - \sum\limits_{i = 1}^{N - K} {\frac{{\Gamma (i,\psi {\zeta _k})}}{{(i - 1)!}}} + }\\ {{\omega _1}\sum\limits_{i = 0}^{N - K} {\frac{{\Gamma (i + 1,\psi {\xi _k}) - \Gamma (i + 1,\psi {\zeta _k})}}{{i!}}} - } \end{array}\\ \begin{array}{*{20}{c}} {{\omega _1}\sum\limits_{i = 1}^{N - K} {\frac{{\Gamma (i,\psi {\xi _k}) - \Gamma (i,\psi {\zeta _k})}}{{(i - 1)!}}} - }\\ {{\omega _2}{\psi ^{ - 1}}\sum\limits_{i = 0}^{N - K} {\frac{{\Gamma (i + 2,\psi {\xi _k}) - \Gamma (i + 2,\psi {\zeta _k})}}{{i!}} + } } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\omega _2}{\psi ^{ - 1}}\sum\limits_{i = 1}^{N - K} {\frac{{\Gamma (i + 1,\psi {\xi _k}) - \Gamma (i + 1,\psi {\zeta _k})}}{{(i - 1)!}}} \end{array} $ | (16) |
基于每个用户的块错误概率,利用文献[13]中基于BCD和CCCP的迭代算法,对WET阶段中的时隙数和WIT阶段中的功率分配系数因子进行联合优化,实现总块错误概率的最小化.优化问题可以表示为
| $ {{\rm{(P1)}}:\mathop {{\rm{min}}}\limits_{m,{\beta _k} \ge 0,k = 1,2, \cdots ,K} {\varepsilon _0} = \sum\limits_{k = 1}^K {{\varepsilon _k}} } $ | (17a) |
| $ {{\rm{ s}}{\rm{.t}}{\rm{. }}\sum\limits_{k = 1}^K {{\beta _k}} = 1} $ | (17b) |
| $ {n \ge 100} $ | (17c) |
| $ {0 < \delta \le {\delta _{{\rm{max}}}}} $ | (17d) |
式(17b)为功率分配系数的约束,式(17c)是由于式(9)仅在n大于100时才成立,式(17d)指定了最大的时延约束.由式(8)可以看出,时延δ直接受WET和WIT阶段的时隙数影响.因此,约束条件式(17d)可以写为0 < m+n≤s,s为WEI和WIT阶段最大的总时隙数.优化问题(P1)重新表示为
| $ \begin{array}{*{20}{c}} {{\rm{(P2)}}:\mathop {{\rm{min}}}\limits_{m,{\beta _k} \ge 0,k = 1,2, \cdots ,K} {\varepsilon _0} = \sum\limits_{k = 1}^K {{\varepsilon _k}} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\sum\limits_{k = 1}^K {{\beta _k}} = 1}\\ {n \ge 100}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < m + n \le s} \end{array} $ | (18) |
(P2) 是一个非凸问题,获得全局最优解时较为复杂.为了有效地解决问题(P2),采用BCD算法得到局部最优解,再通过迭代算法获得全局最优解.首先,把问题(P2)分为2个子问题:
| $ \begin{array}{l} \begin{array}{*{20}{c}} {({\rm{P2 - a}}):\mathop {\min }\limits_m {\varepsilon _0} = \sum\limits_{k = 1}^K {{\varepsilon _k}} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}n \ge 100}\\ {0 < m + n \le s} \end{array}\\ \begin{array}{*{20}{c}} {({\rm{P2 - b}}):\mathop {{\rm{min}}}\limits_{{\beta _k} \ge 0,k = 1,2, \cdots ,K} {\varepsilon _0} = \sum\limits_{k = 1}^K {{\varepsilon _k}} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\sum\limits_{k = 1}^K {{\beta _k}} = 1} \end{array} \end{array} $ |
其中(P2-a)是给定βk的m的优化子问题,需要在同时满足WIT阶段时隙数n和最大时延s的约束条件下,求得最优时隙数m;(P2-b)是给定m的βk的优化子问题,在所有用户块长度都为M的条件下,进行合理的功率分配,使总块错误概率最小化.然后,迭代求解(P2-a)和(P2-b).
在第1次迭代中,初始化βk=βk(t),求解(P2-a),并获得最优解m,作为m(1).然后,令m=m(1),求解(P2-b)并获得局部最优解βk,作为βk(1).
在第t(t>1)次迭代中,通过采用βk=βk(t-1),求解(P2-a),并将最优m更新为m(t);然后,通过采用m=m(t),求解(P2-b),并将βk更新为βk(t).当ε0收敛时,迭代停止.
2.2 (P2-a)的优化通过式(5)和
| $ \frac{{{\partial ^2}{\varepsilon _k}}}{{\partial {m^2}}} = \frac{{{\partial ^2}{\varepsilon _k}}}{{\partial {\psi ^2}}}{\left( {\frac{{\partial \psi }}{{\partial m}}} \right)^2} + \frac{{\partial {\varepsilon _k}}}{{\partial \psi }}\frac{{{\partial ^2}\psi }}{{\partial {m^2}}} $ | (19) |
其中:
| $ \frac{{\partial {\varepsilon _k}}}{{\partial \psi }} = \frac{{{\omega _2}{\psi ^{ - 2}}[\Gamma (N - K + 2,\psi {\xi _k}) - \Gamma (N - K + 2,\psi {\zeta _k})]}}{{(N - K)!}} $ | (20) |
| $ \begin{array}{*{20}{c}} {\frac{{{\partial ^2}{\varepsilon _k}}}{{{\partial ^2}\psi }} = - \frac{{\zeta _k^{N - K + 1}{\psi ^{N - K - 1}}{{\rm{e}}^{ - \psi {\zeta _k}}}}}{{(N - K)!}} + }\\ {\frac{{{\omega _2}\xi _k^{N - K + 1}{\psi ^{N - K - 1}}{{\rm{e}}^{ - \psi {\xi _k}}}}}{{(N - K)!}} + ( - 2)(N - K + 1) \times }\\ {{\omega _2}{\psi ^{ - 3}}[\Gamma (N - K + 2,\psi {\xi _k}) - \Gamma (N - K + 2,\psi {\zeta _k})]} \end{array} $ | (21) |
由Γ(N-K+2, ψξk)-Γ(N-K+2, ψζk)>0,ω2, ψ, ξk, ζk>0,可得
| $ {\frac{{\partial L(m,{\beta _k},\lambda )}}{{\partial m}} = \frac{{\partial {\varepsilon _k}}}{{\partial m}} - \lambda = 0} $ | (22a) |
| $ {\lambda (s - n - m) = 0} $ | (22b) |
其中
| $ \begin{array}{*{20}{c}} {\frac{{\partial {\varepsilon _k}}}{{\partial m}} = \frac{{\partial {\varepsilon _k}\partial \psi }}{{\partial \psi }}\frac{{{\partial _2}\eta BP{\lambda _1}{\beta _k}{\varOmega _k}}}{{\sigma _k^2n}} \times }\\ {[\Gamma (N - K + 2,\psi {\xi _k}) - \Gamma (N - K + 2,\psi {\zeta _k})]}\\ {(N - K)!} \end{array} $ | (23) |
通过式(22a)得到
| $ {m^*} = s - n $ | (24) |
(P2-b)是一个非凸优化问题,通过CCCP算法[15],可以近似迭代的方式解决. CCCP算法的基本思想是通过迭代的方式将原问题近似为具有一阶泰勒级数展开的凸问题,并求解近似凸问题,直到收敛.
首先,令β0为初始值,βi=[βi, 1, βi, 2, …, βi, K]T(i≥1)为第i次迭代的最优值;然后,在第i次迭代时,εk的一阶泰勒级数展开可以表示为
| $ \begin{array}{l} {\varepsilon _k}({\beta _{i,k}}) = {\varepsilon _k}({\beta _{i - 1,k}}) + \nabla [{\varepsilon _k}({\beta _{i - 1,k}})]({\beta _{i,k}} - {\beta _{i - 1,k}}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\nabla ^2}[{\varepsilon _k}({\beta _{f,k}})]{({\beta _{i,k}} - {\beta _{i - 1,k}})^2} \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varepsilon _k}({\beta _{i - 1,k}}) + \nabla [{\varepsilon _k}({\beta _{i - 1,k}})]({\beta _{i,k}} - {\beta _{i - 1,k}}) \buildrel \Delta \over = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varepsilon _k}({\beta _{i,k}};{\beta _{i - 1,k}}) \end{array} $ | (25) |
其中:βf, k表示βi-1, k和βi, k之间的一个数;
| $ {\varepsilon _0}(m,\mathit{\boldsymbol{\beta }}) \le \sum\limits_{k = 1}^K {{\varepsilon _k}} ({\beta _{i,k}};{\beta _{i - 1,k}}) \buildrel \Delta \over = {\varepsilon _{hb}}(m,\mathit{\boldsymbol{\beta }};{\mathit{\boldsymbol{\beta }}_{i - 1}}) $ | (26) |
进而,通过优化β,使上界函数εhb(m, β; βi-1)最小化,代替了最小化ε0(m, β).最小化上界函数εhb(m, β; βi-1)可以表示为
| $ ({\rm{P2}} - {\rm{c}}):\mathop {{\rm{min}}}\limits_{{\beta _k} \ge 0,k = 1,2, \cdots ,K} {\varepsilon _{hb}}(m,\mathit{\boldsymbol{\beta }};{\mathit{\boldsymbol{\beta }}_{i - 1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}} $ |
ε0(m, β; βi-1)也是一个凹函数,同时,约束条件(17b)是一个仿射集.因此,(P2-c)是一个凸优化问题.
在使系统的总块错误概率最小化时,需要在每个用户满足各自可靠性需求的前提下,对功率分配系数进行优化. γmink为用户k所需的最小SNR,因此,每个用户的SNR需要满足
| $ {\gamma _k} \ge \gamma _{{\rm{min}}}^k,k = 1,2, \cdots ,K $ | (27) |
根据式(7),上面的约束条件可以转换为
| $ {\beta _k} \ge \frac{{\gamma _{\min }^k\sigma _k^2}}{{{P_{\rm{S}}}|h_k^\dagger \prod\nolimits_k {{\mathit{\boldsymbol{h}}_k}} |}} $ | (28) |
因此,优化问题(P2-c)可以重新表示为
| $ ({\rm{P2}} - {\rm{d}}):\mathop {{\rm{min}}}\limits_{{\beta _k} \ge 0,k = 1,2, \cdots ,K} {\varepsilon _0}(m,\mathit{\boldsymbol{\beta }};{\mathit{\boldsymbol{\beta }}_{i - 1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rm{17b}}),({\rm{28}}) $ |
ε0(m, β; βi-1)的最小化即等同于εk(βi, k; βi-1, k)的最小化.
通过计算得
通过拉格朗日对偶算法对问题(P2-d)进行求解.首先,构造拉格朗日函数L(m, βk, λ)=εk+
| $ {\frac{{\partial {\rm{L}}(m,{\beta _k},\lambda )}}{{\partial {\beta _k}}} = \frac{{\partial {\varepsilon _k}}}{{\partial {\beta _k}}} + \alpha - \chi = 0} $ | (29) |
| $ {\alpha \left( {{\beta _k} - \frac{{\gamma _{{\rm{min}}}^k\sigma _k^2}}{{{P_{\rm{S}}}|\mathit{\boldsymbol{h}}_k^\dagger \prod\limits_k {{\mathit{\boldsymbol{h}}_k}} |}}} \right) = 0} $ | (30) |
| $ {\alpha \ge 0} $ | (31) |
| $ {\chi \left( {1 - \sum\limits_{k = 1}^K {{\beta _k}} } \right) = 0} $ | (32) |
| $ {\chi \ge 0} $ | (33) |
类似于式(29)、式(30)和式(32)的推导,可以证明,为了导出问题(P2-d)的最优解,约束式(28)应该是等式.基于此,可以得到βk的闭型表达式为
| $ {{\beta _k} = \frac{{\gamma _{{\rm{min}}}^k\sigma _k^2}}{{{P_{\rm{S}}}|\mathit{\boldsymbol{h}}_k^\dagger \prod\limits_k {{\mathit{\boldsymbol{h}}_k}} |}}} $ | (34) |
最后问题(P2-d)的最优解为
| $ {\beta _k} = \left\{ {\begin{array}{*{20}{l}} {\frac{{\gamma _{{\rm{min}}}^k\sigma _k^2}}{{{P_{\rm{S}}}\left| {\mathit{\boldsymbol{h}}_k^\dagger \prod\limits_k {{\mathit{\boldsymbol{h}}_k}} } \right|}},\quad 1 \le k \le K - 1}\\ {1 - \sum\limits_{i = 1}^{K - 1} {{\beta _i}} ,\quad k = K} \end{array}} \right. $ | (35) |
算法1为解决问题(P1)的具体过程,步骤5~7是解决问题(P2-b)的迭代过程,步骤2~9是解决问题(P2-a)的迭代过程.
算法1 优化问题(P1)的迭代算法
1 初始化β=β(0),t=1.
2 repeat
3 设置β=β(t-1),利用式(24)计算m(t).
4 设置m=m(0),β0=β(t-1),i=1.
5 repeat
6 给定βi,利用式(33)计算βi+1,并且i←i+1.
7 until β收敛.
8 β(t)=βi*,并且t←t+1.
9 until
为了保证算法1的收敛性,在这一部分需要证明ε0(m(t+1), β(t+1))≤ε0(m(t), β(t)).在BCD算法的每次迭代中都存在CCCP算法,因此将首先证明CCCP算法在BCD算法第t次迭代中的收敛.令βi+1为CCCP算法第i+1次迭代时,问题(P2-b)的最优解,可以得到
| $ \begin{array}{*{20}{c}} {{\varepsilon _{hb}}({m^{(t)}},{\mathit{\boldsymbol{\beta }}_{i + 1}};{\mathit{\boldsymbol{\beta }}_i}) = }\\ {\left\{ {\mathop {{\rm{min}}}\limits_{{\beta _k} \ge 0,k = 1,2, \cdots ,K} {\varepsilon _{hb}}({m^{(t)}},\mathit{\boldsymbol{\beta }};{\mathit{\boldsymbol{\beta }}_{i - 1}})} \right\} \le }\\ {{\varepsilon _{hb}}({m^{(t)}},{\mathit{\boldsymbol{\beta }}_i};{\mathit{\boldsymbol{\beta }}_i})} \end{array} $ | (36) |
由于εhb(m, β; βi-1)是ε0(m, β)的上界,所以
| $ {\varepsilon _{hb}}({m^{(t)}},{\mathit{\boldsymbol{\beta }}_i};{\mathit{\boldsymbol{\beta }}_i}) = {\varepsilon _0}({m^{(t)}},{\mathit{\boldsymbol{\beta }}_i}) \le {\varepsilon _{hb}}({m^{(t)}},{\mathit{\boldsymbol{\beta }}_i};{\mathit{\boldsymbol{\beta }}_{i - 1}}) $ | (37) |
通过式(24)和式(25)可以得到
| $ {\varepsilon _{hb}}({m^{(t)}},{\mathit{\boldsymbol{\beta }}_{i + 1}};{\mathit{\boldsymbol{\beta }}_i}) \le {\varepsilon _{hb}}({m^{(t)}},{\mathit{\boldsymbol{\beta }}_i};{\mathit{\boldsymbol{\beta }}_{i - 1}}) $ | (38) |
保证了在BCD算法的每次迭代中CCCP算法的收敛.
接下来证明BCD算法的收敛性.令mi+1为CCCP算法第i+1次迭代时,问题(P2-a)的最优解.因此,可以得到
| $ \begin{array}{*{20}{c}} {{\varepsilon _0}({m^{(t + 1)}},{\mathit{\boldsymbol{\beta }}^{(t)}}) = \{ \mathop {{\rm{min}}}\limits_m {\varepsilon _0}(m,{\mathit{\boldsymbol{\beta }}^{(t)}})\} \le }\\ {{\varepsilon _0}({m^{(t)}},{\mathit{\boldsymbol{\beta }}^{(t)}})} \end{array} $ | (39) |
通过式(24)~式(27)可以得到ε0(m(t+1), β(t+1))≤ε0(m(t), β(t)),即证明了算法1的收敛性.
3 仿真结果为了描述路径衰落的影响,信道衰落模型为Ωk=10-3/(1+dkω),其中Ωk为源节点S到用户k之间的平均信道功率增益,dk为源结点S到用户k之间的距离,ω为路径损耗系数.假设ET-S的距离设定为12 m,带宽为1 MHz,每个时隙的持续时间Tc=1 μs.在WET阶段,能量发射器ET的发射功率PET=30 dBm.能量捕获效率η=0.5,路径衰落因子ω1=2.在WIT阶段,总用户数K=3,路径损耗系数ω2=3、噪声功率σk2=-80 dBm,源节点S与每个用户传输的信息量分别为υ1=600,υ2=800,υ3=1 000,传输距离d1=100,d2=80,d3=130.
图 2所示为源节点S的传输功率PS与WET阶段的时隙数m的关系.可以看出,PS除了受时隙数m的影响外,还会受到发射天线NET和接收天数N的影响.在相同时隙下,传输功率随着天线数量的增加而增大,同时也发现,当发射天线NET和接收天线N的数值进行互换时,两条区间几乎重合,说明RF信号收发端的天线数对PS具有相同的影响.
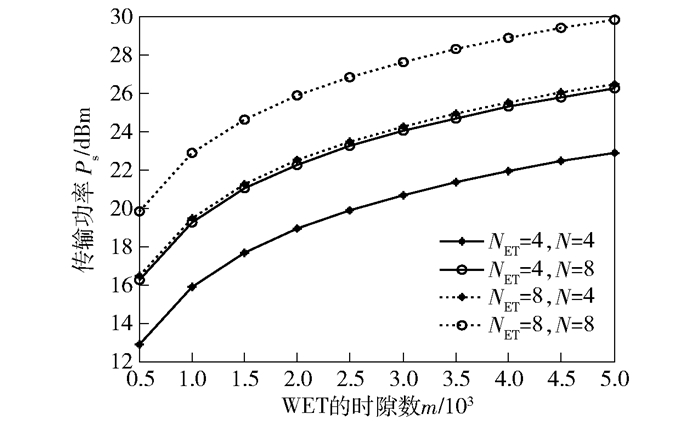
|
图 2 传输功率PS与WET时隙数m的关系 |
图 3所示为不同传输功率PS所对应的块错误概率εk.其中,功率分配系数βk=1/3, ∀k,传输距离dk=100,传输的信息量υ=600 bit.可以发现,随着源节点传输功率PS的增大,用户k的块错误概率εk越小.同时,发现源节点S的天线数量N和数据包的长度M都会影响到εk.当传输功率PS、数据包长度M一定时,天线数量N越多,块错误概率εk越小;当传输功率PS、天线数量N一定时,数据包长度M越长,块错误概率εk越小.因此,可以通过增加传输功率PS、天线数量N和数据包长度M来减少块错误概率εk,提高系统的可靠性.
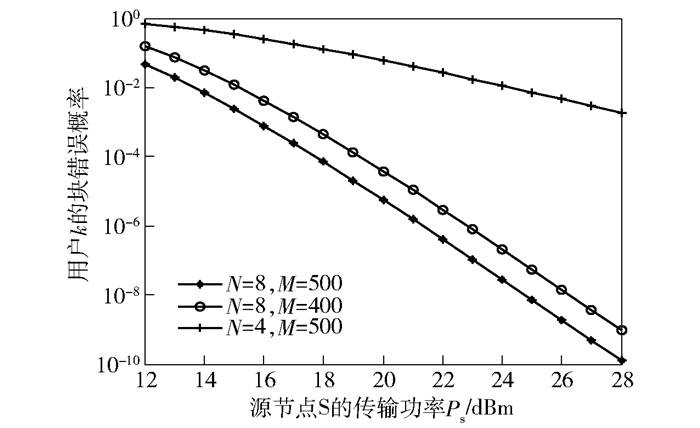
|
图 3 用户k的块错误概率与传输功率PS的关系 |
图 4所示为用户k的错误概率εk与WIT时隙数n的关系.从仿真图中发现,刚开始随着时隙数n的增大,用户k的错误概率εk急剧减少,但是当n≥1 000时,随着n的增大,εk的变化速率越来越缓慢.从仿真图中还发现,源节点S的天线数相比ET的电线数对用户的块错误概率影响较大,在ET天线数一定时,增加S端的天线数量,用户的块错误概率显著减小.
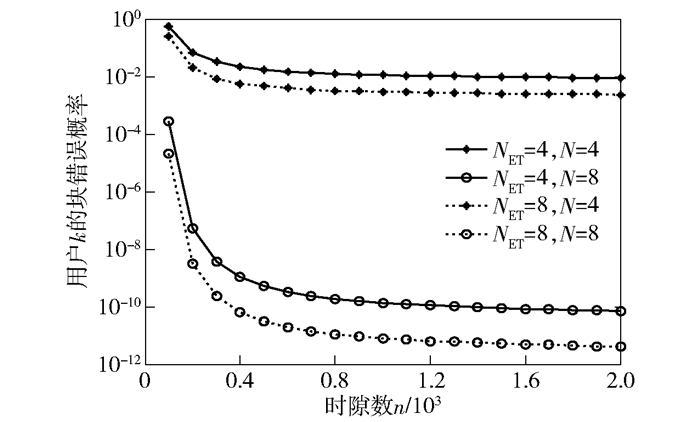
|
图 4 用户k的块错误概率与时隙数n的关系 |
从图 4中发现,WIT时隙数n为1 000时,信息传输的可靠性较好.因此,令n=1 000,其他参数保持不变. 图 5所示为总块错误概率ε0与WEI和WIT阶段总时隙数s的关系.从图 5中可以明确的观察到,随着总时隙数s的增加,总块错误概率不断减小,这意味着系统的时延越大,错误概率越小,信息传输的可靠性越高.在时延一定时,可以通过增加WIT阶段的时隙数,来增加数据包的长度,降低用户的块错误概率,进而提高系统的可靠性.可以根据实际情况的需求,使系统的时延和可靠性进行权衡,得到最佳状态.同时,通过仿真图发现,在对系统整体进行分析时,源节点的天线数量对系统的可靠性影响比较大,这与图 2、图 4对天线数量的分析结果一致.因此,可以通过增加源节点的天线数量来减少系统的块错误概率,提高系统的可靠性.
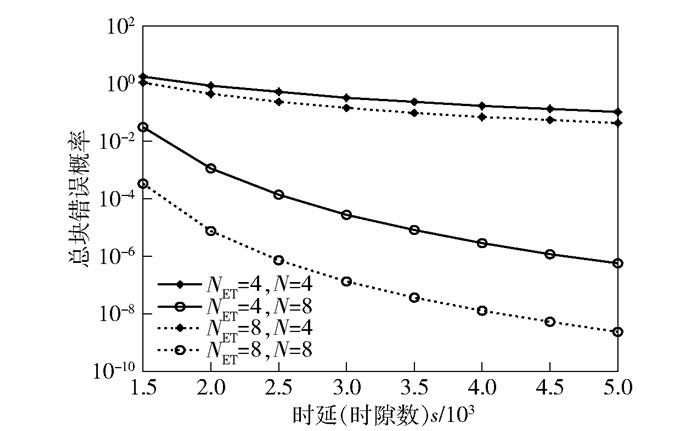
|
图 5 总块错误概率与总时隙数s的关系 |
研究了短包通信场景下多用户无线能量传输系统的块错误概率.推导出每个用户块错误率的近似闭合形式表达式,并验证了其准确性.根据闭合表达式,分析影响块错误概率的因素,得到可以通过优化发射天线数量、数据包长度以及发射功率提高用户的块错误概率,同时也可以优化系统的功率分配系数,提高系统的块错误概率.此外,通过仿真验证了块错误概率和时延的关系.结果表明,可靠性越严格,需要WET的时隙数越多,进而延迟越高.同时发现,当时延一定时,可以通过增加数据包长度减少系统的块错误概率,为系统的时延和可靠性的权衡提供了理论依据.
| [1] |
Durisi G, Koch T, Popovski P. Toward massive, ultrareliable, and low-latency wireless communication with short packets[J]. Proceedings of the IEEE, 2016, 104(9): 1711-1726. DOI:10.1109/JPROC.2016.2537298 |
| [2] |
Devassy R, Durisi G, Popovski P, et al. Finite-block length analysis of the ARQ-protocol throughput over the gaussian collision channel[C]//International Symposium on Communications, Control and Signal Processing (ISCCSP). Athens: IEEE Press, 2014: 173-177.
|
| [3] |
Khan T A, Heath R W, Popovski P. Wirelessly powered communication networks with short packets[J]. IEEE Transactions on Communications, 2017, 65(12): 5529-5543. DOI:10.1109/TCOMM.2017.2742512 |
| [4] |
Lopez O L A, Fernandez E M G, Souza R D, et al. Wireless powered communications with finite battery and finite blocklength[J]. IEEE Transactions on Communications, 2018, 66(4): 1803-1816. DOI:10.1109/TCOMM.2017.2786673 |
| [5] |
Lopez O L A, Alves H, Souza R D, et al. Ultra-reliable short-packet communications with wireless energy transfer[J]. IEEE Signal Processing Letters, 2018, 18(5): 2161-2177. |
| [6] |
Yang Wei, Durisi G, Koch T, et al. Quasi-static multiple-antenna fading channels at finite blocklength[J]. IEEE Transactions on Information Theory, 2014, 60(7): 4232-4265. DOI:10.1109/TIT.2014.2318726 |
| [7] |
Gu Yifan, Chen He, Li Yonghui, et al. Multiuser MIMO short-packet communications: time-sharing or zero-forcing beamforming?[C]//International Conference on Communications (ICC). Kansas City: IEEE Press, 2018: 1-6.
|
| [8] |
Hu Yulin, Serror M, Wehrle K, et al. Finite blocklength performance of cooperative multi-terminal wireless industrial networks[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5778-5792. DOI:10.1109/TVT.2018.2794178 |
| [9] |
Xu Jie, Zhang Rui. A general design framework for MIMO wireless energy transfer with limited feedback[J]. IEEE Transactions on Signal Processing, 2016, 64(10): 2475-2488. DOI:10.1109/TSP.2016.2526965 |
| [10] |
Makki B, Svensson T, Zorzi M. Finite block-length analysis of the incremental redundancy HARQ[J]. IEEE Wireless Communications Letters, 2014, 3(5): 529-532. DOI:10.1109/LWC.2014.2353059 |
| [11] |
Zhu Guangxu, Zhong Caijun, Suraweera H A, et al. Outage probability of dual-hop multiple antenna AF aystems with linear processing in the presence of co-channel interference[J]. IEEE Transactions on Wireless Communications, 2014, 13(4): 2308-2321. DOI:10.1109/TWC.2014.030514.131497 |
| [12] |
Gradshteyn I S, Ryzhik I M. Table of integrals, series and products[J]. Mathematics of Computation, 2007, 20(96): 1157-1160. |
| [13] |
Chen Jie, Zhang Lin, Liang Yingchang, et al. Resource allocation for wireless-powered IoT networks with short packet communication[J]. IEEE Transactions Wireless Communications, 2019, 18(2): 1447-1461. DOI:10.1109/TWC.2019.2893335 |
| [14] |
Boyd S, Vandenberghe L. Convex optimization[M]. New York: Cambridge University Press, 2004.
|
| [15] |
Bharath K, Sriperumbudur, Gert R G. Lanckriet. On the convergence of the concave-convex procedure[C]//International Conference on Neural Information Processing Systems.[S.l.]: Curran Associates Inc, 2009: 1759-1767.
|



