针对空间相关信道下存在干扰机的多用户大规模多输入多输出系统,研究了基站仅配置低精度模数转换器(ADC)的系统频谱效率性能.通过结合指数(Toeplitz)相关模型建立空间相关信道,并利用加性量化噪声模型和最大比合并算法,推导出系统频谱效率的闭合表达式.基于此,进一步对理想和非理想信道状态信息下的系统频谱效率进行比较分析.仿真结果表明,随着用户发送功率和ADC精度的增加,频谱效率将出现饱和效应;当合法用户发送功率小于干扰机发送功率时,干扰机对系统的影响占主导作用;当合法用户发送功率大于干扰机发送功率时,能够有效地抑制干扰机对系统的影响.
Aiming at multi-user massive multi-input multi-output systems with jammer under spatial correlation channel, where the system spectral efficiency performance of the base station with low-resolution analog-to-digital converters (ADCs) is studied. Establishing spatial correlation channel by combining exponential Toeplitz correlation models, utilizing the additive quantization noise model and the maximum ratio combination algorithm, a closed expression of the spectral efficiency is derived. The system spectral efficiency under ideal/non-ideal channel state information is analyzed thereafter. Simulation shows that the spectral efficiency will have a saturation effect as the transmit power of the user and the resolution of the ADC increase; when the transmit power of the user is less than the transmit power of the jammer, the influence of the jammer on the system is dominant; when the transmit power of the user is greater than the transmit power of the jammer, it can effectively suppress the influence of the jammer on the system.
大规模多输入多输出(MIMO, multi-input multi-output)技术作为5G移动通信系统的一项关键技术,具有显著提高系统吞吐率、频谱效率和能量效率等性能的潜力[1].现如今,随着无线通信技术不断地革新,用户对系统容量的需求也不断地提高,通过部署大型天线阵列可以提升系统频谱效率,同时带来了信道空间相关等问题.为缓解该问题对系统造成的性能影响,学者们已经开展了一些相关研究[2-4]. zdogan等[2]研究莱斯空间相关信道下多小区多用户大规模MIMO系统,并推导出上/下行链路频谱效率表达式. Xu等[3]研究瑞利空间相关信道下分布式节能功率分配方案,并推导出精确的能量效率闭合表达式. Alshammari等[4]研究空间相关性对时分复用系统频谱效率的影响,并指出考虑空间相关的系统频谱效率低于理想系统.
此外,传统大规模MIMO基站通常部署了大量天线和高精度模数转换器(ADC, Analog-to-digital converters),这有效地消除了量化噪声对系统的影响,但导致系统硬件成本和功率损耗呈指数级增长.陶成等[5]利用加性量化噪声模型(AQNM, additive quantization noise model)将低精度ADC非线性量化函数关系转化成线性量化函数关系. Xu等[6]采用AQNM和MRC算法研究低精度ADC对系统的影响,并推导出系统可实现速率近似表达式. Fan等[7]和Zhang等[8]提出瑞利信道和莱斯信道场景下配置低精度ADC量化时,通过适当地增加基站天线阵列可以提高系统频谱效率.然而,现有关于低精度ADC大规模MIMO系统性能的研究,几乎都是建立在理想瑞利信道或莱斯信道下进行的,尚未考虑信道的空间相关性对频谱效率的影响.
基于上述分析,针对干扰机和空间相关信道下低精度ADC大规模MIMO上行系统的研究与分析.首先,采用指数Toeplitz相关模型对信道建模,利用AQNM和MRC算法处理基站信号,并借助大数定律推导出系统频谱效率的近似表达式.然后,基于得到的近似结果,通过适当地调整系统参数,对系统性能进一步展开分析.最后,在理想/非理想信道状态信息(CSI, channel status information)下,对空间相关信道、瑞利信道及莱斯信道场景下的频谱效率进行比较分析,并指出适当地增加基站天线数和用户发送功率可以消除低精度ADC引起的量化误差和弥补信道空间相关性造成的系统性能损失.
1 系统模型 1.1 空间相关信道建模研究单小区多用户大规模MIMO上行系统,假设系统中有K个单天线用户同时向基站传输数据,且各用户之间相互独立,而基站端有M根接收天线组成.根据Kronecker相关模型[9],则空间相关信道模型可以表示为
| $ \mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{R}}^{\frac{1}{2}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{D}}^{\frac{1}{2}}} $ | (1) |
其中:R∈CM×M为信道相关矩阵;H∈CM×K为小尺度衰落系数矩阵,其元素为独立同分布的随机变量,服从零均值、单位方差的复高斯分布;D为K×K维实对角矩阵,其对角线元素[D]kk=βk为第k用户到基站的大尺度衰落;C为复数矩阵.
根据Toeplitz相关模型[10],则R的第(m, n)个元素可以表示为
| $ {[\mathit{\boldsymbol{R}}]_{mn}} = \left\{ {\begin{array}{*{20}{l}} {{\gamma ^{n - m}},}&{m \le n}\\ {{{({\gamma ^{m - n}})}^*},}&{m > n} \end{array}} \right. $ | (2) |
其中:上标*表示共轭运算;γ值为基站天线间的相关系数,即0≤γ≤1.显然,γ=0表示相邻天线间空间不相关;γ=1表示相邻天线间空间全相关.
1.2 上行链路模型假设基站端配置M根天线,信号发送端有K个单天线用户和一个单天线干扰机.所有用户都使用相同的时频资源,则在基站端接收到的信号矢量y∈CM×1可以表示为
| $ \mathit{\boldsymbol{y}} = \sqrt {{p_{\rm{u}}}} \mathit{\boldsymbol{Fx}} + \sqrt {{q_{\rm{u}}}} {\mathit{\boldsymbol{g}}_w}\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{n}} $ | (3) |
其中:pu为用户平均发送功率,qu为干扰机信号发送功率,F∈CM×K为用户到基站之间的信道矩阵,gw~CN(0, βwIM)为干扰机到基站之间的信道矩阵,其中βw为干扰机大尺度衰落;x∈CK×1为用户发送的信号,且满足E{xxH}=IK, s为干扰机发送信号,且满足E{ssH}=1;n~CN(0, σ2IM)为复加性高斯白噪声(AWGN, additive white Gaussian noise),其中IA(A∈{K, M})表示A×A维单位矩阵.随后采用AQNM对信号进行量化处理yq=Q(y),则经过低精度ADC量化后的输出信号可以表示为
| $ {\mathit{\boldsymbol{y}}_q} \approx \alpha \sqrt {{p_{\rm{u}}}} \mathit{\boldsymbol{Fx}} + \alpha \sqrt {{q_{\rm{u}}}} {\mathit{\boldsymbol{g}}_w}\mathit{\boldsymbol{s}} + \alpha \mathit{\boldsymbol{n}} + {\mathit{\boldsymbol{n}}_q} $ | (4) |
其中:Q(·)表示低精度量化函数;α=1-ρ为线性量化增益系数,ρ为ADC量化失真因子,其取值取决于ADC量化位数[8];nq~CN(0, Rnq)是与输出信号yq不相关的加性高斯量化噪声.
对于固定的信道矩阵F,则量化噪声nq的协方差矩阵为[8]
| $ {\mathit{\boldsymbol{R}}_{{\mathit{\boldsymbol{n}}_q}}} = \alpha \rho {\rm{diag}} ({p_{\rm{u}}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}} + {\sigma ^2}{\mathit{\boldsymbol{I}}_M}) $ | (5) |
其中H表示共轭转置运算.
2 频谱效率性能分析由于MRC算法计算复杂度小且具有较好的鲁棒性,所以在基站端采用AQNM和MRC来获得检测后的量化信号.首先在理想CSI下推导出频谱效率的闭合表达式;然后通过调整系统参数设置对系统频谱效率进行分析;最后进一步分析非理想CSI下估计误差对系统性能的影响.
2.1 理想CSI下频谱效率表达式推导式(4)中的信号经过最大比合并r=FHy后,即基站端接收到的总信号为r,其最大比合并矩阵为FH,则系统中第k个用户的输出信号为
| $ \begin{array}{l} {r_k} = \underbrace {\alpha \sqrt {{p_{\rm{u}}}} \mathit{\boldsymbol{f}}_k^{\rm{H}}{\mathit{\boldsymbol{f}}_k}{x_k}}_{{\rm{用户}}k{\rm{发送的信号}}} + \underbrace {\alpha \sqrt {{p_{{\rm{ u }}}}} \sum\limits_{i = 1,i \ne k}^K {\mathit{\boldsymbol{f}}_k^{\rm{H}}} {\mathit{\boldsymbol{f}}_i}{x_i}}_{{\rm{来自其他用户的干扰信号}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underbrace {\alpha \sqrt {{q_{\rm{u}}}} \mathit{\boldsymbol{f}}_k^{\rm{H}}{g_w}\mathit{\boldsymbol{s}}}_{{\rm{来自干扰机的信号}}} + \underbrace {\alpha \mathit{\boldsymbol{f}}_k^{\rm{H}}\mathit{\boldsymbol{n}}}_{{\rm{AWGN}}} + \underbrace {\mathit{\boldsymbol{f}}_k^{\rm{H}}{\mathit{\boldsymbol{n}}_q}}_{{\rm{量化噪声}}} \end{array} $ | (6) |
其中:xk是第k个用户发送的信号,fk为空间相关信道F的第k列元素.等式右边第1项为用户k发送的信号,第2项为来自其他用户的干扰信号,第3项为来自干扰机的信号,第4项为信道噪声,最后1项为量化噪声.
理想CSI条件下,第k个用户在大规模MIMO上行系统频谱效率为
| $ {R_k} = E\left\{ { {\rm{lb}} \left( {1 + \frac{{{A_k}}}{{{B_k} + {C_k} + {D_k} + {E_k}}}} \right)} \right\} $ | (7) |
其中:
定理1 在干扰机和空间相关信道场景下的低精度ADC大规模MIMO系统,若基站端采用MRC算法处理用户发送数据,则第k个用户在大规模MIMO上行系统频谱效率可以近似为
| $ \begin{array}{*{20}{c}} {{R_k} \approx }\\ {{\rm{lb}}\left( {1 + \frac{{\alpha {p_{\rm{u}}}{\beta _k}\vartheta }}{{\alpha {p_{\rm{u}}}\tau \sum\limits_{i = 1,i \ne k}^K {{\beta _i}} + \left( {{\sigma ^2} + (1 - \alpha ){p_{\rm{u}}}\sum\limits_{i = 1}^K {{\beta _i}} + \kappa } \right)\varphi }}} \right)} \end{array} $ | (8) |
| $ {\vartheta = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^M {(|{r_{mn}}| + {r_{mm}}{r_{nn}})} } + \sum\limits_{m \ne n}^M {\sum\limits_{n = 1}^M {{r_{mn}}} } {r_{nm}}} $ |
| $ {\tau = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^M | } {r_{mn}}{|^2},\varphi = \sum\limits_{m = 1}^M | {r_{mm}}|,\kappa = \alpha {q_{\rm{u}}}{\beta _w}} $ |
同时,rij(i, j∈{m, n})为R的第i行第j列元素.
证明 对于具有庞大天线数量的大规模MIMO系统,可以采用大数定理[11]:
| $ {R_k} \approx {\rm{lb}}\left\{ { 1 + \frac{{E\{ {A_k}\} }}{{E\{ {B_k}\} + E\{ {C_k}\} + E\{ {D_k}\} + E\{ {E_k}\} }}} \right\} $ | (9) |
下面进一步计算式(9)中各项信号的数学期望,其中前4项信号的数学期望分别为
| $ \begin{array}{*{20}{c}} {E\{ {A_k}\} = {\alpha ^2}{p_{\rm{u}}}\beta _k^2 \times }\\ {\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^M {(|{r_{mn}}{|^2} + {r_{mm}}{r_{nn}})} } + \sum\limits_{m = 1}^M {\sum\limits_{n \ne m}^M {{r_{mn}}} } {r_{nm}}} \right)} \end{array} $ | (10) |
| $ {E\{ {B_k}\} = {\alpha ^2}{p_{\rm{u}}}{\beta _k}{\beta _i}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^M | } {r_{mn}}{|^2}} $ | (11) |
| $ {E\{ {C_k}\} = {\alpha ^2}{q_{\rm{u}}}{\beta _k}{\beta _w}\sum\limits_{m = 1}^M | {r_{mm}}|} $ | (12) |
| $ {E\{ {D_k}\} = {\alpha ^2}{\sigma ^2}{\beta _k}\sum\limits_{m = 1}^M | {r_{mm}}|} $ | (13) |
其中rmn为空间相关矩阵R的第(m, n)个元素.
对于最后1项的求解,假设当
| $ E\{ {E_k}\} = \alpha \rho {\beta _k}\left( {{p_{\rm{u}}}\sum\limits_{i = 1}^K {{\beta _i}} + {\sigma ^2}} \right)\sum\limits_{m = 1}^M | {r_{mm}}| $ | (14) |
最后,将式(10)~(14)代入式(9),即可得到式(8),证毕.
相应地,系统中K个用户总的频谱效率为
| $ {R_{{\rm{sum}}}} = \sum\limits_{k = 1}^K {{R_k}} $ | (15) |
由2.1节推导得出的式(8)可知,低精度ADC大规模MIMO系统频谱效率受多个因素共同影响.为进一步验证上述系统参数对频谱效率的影响,将对该表达式进一步化简与分析,并得到以下推论.
推论1 固定基站天线数M、空间相关系数γ和ADC量化位数b不变,当用户发送功率pu→∞,则式(8)的频谱效率可以简写为
| $ {R_k} \to {\rm{lb}}\left( { 1 + \frac{{\alpha {\beta _k}\vartheta }}{{\alpha \tau \sum\limits_{i = 1,i \ne k}^K {{\beta _i}} + (1 - \alpha )\varphi \sum\limits_{i = 1}^K {{\beta _i}} }}} \right) $ | (16) |
从式(16)可知,随着用户发送功率pu的逐渐增大,频谱效率趋于一个常数,其具体数值取决于ADC量化位数b和空间相关系数γ.此时,频谱效率与低精度ADC量化误差及信道空间相关性紧密相关,考虑已知条件中用户发送功率趋于无穷,因此采用低精度ADC引起的频谱效率损失并不能仅通过增大用户信号发送功率来补偿.
推论2 固定基站天线数M、用户发送功率pu和空间相关系数γ不变,当仅考虑全精度ADC时,即b→∞,则式(8)的频谱效率可以简写为
| $ {R_k} \approx {\rm{lb}} \left( {1 + \frac{{{p_{\rm{u}}}{\beta _k}\vartheta }}{{{p_{\rm{u}}}\tau \sum\limits_{i = 1,i \ne k}^K {{\beta _i}} + ({\sigma ^2} + {q_{\rm{u}}}{\beta _w})\varphi }}} \right) $ | (17) |
从式(17)可知,当仅考虑全精度ADC时,大规模MIMO系统的量化噪声可以忽略不计.此时,随着用户发送功率pu的逐渐增大,频谱效率趋于一个常数,其具体数值仅取决于空间相关系数γ的取值.
推论3 固定基站天线数M、用户发送功率pu和ADC量化位数b不变,当空间相关系数γ=0时,即R=I.因此,式(8)的频谱效率可以简写为
| $ \begin{array}{*{20}{c}} {{R_k} \to }\\ {{\rm{lb}}\left( {1 + \frac{{\alpha {p_{\rm{u}}}{\beta _k}(M + 1)}}{{\alpha {p_{\rm{u}}}\sum\limits_{i = 1,i \ne k}^K {{\beta _i}} + {\sigma ^2} + (1 - \alpha ){p_{\rm{u}}}\sum\limits_{i = 1}^K {{\beta _i}} + \kappa }}} \right)} \end{array} $ | (18) |
在不考虑干扰机的情况下,即κ=0.通过假设
对非理想CSI下的大规模MIMO上行系统研究,采用一种典型信道模型[12]:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat r}}}_k} = \underbrace {\alpha \sqrt {{p_u}} \mathit{\boldsymbol{\hat f}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat f}}}_k}{x_k}}_{{\rm{用户}}k{\rm{发送的信号}}} + \underbrace {\alpha \sqrt {{p_{\rm{u}}}} \sum\limits_{i = 1}^K {\mathit{\boldsymbol{\hat f}}_k^{\rm{H}}} {{\mathit{\boldsymbol{\hat f}}}_i}{x_i}}_{{\rm{来自其他用户的干扰信号}}} + \\ \underbrace {\alpha \sqrt {{q_{\rm{u}}}} \mathit{\boldsymbol{\hat f}}_k^{\rm{H}}{\mathit{\boldsymbol{g}}_w}s}_{{\rm{来自干扰机的信号}}} + \underbrace {\alpha \sqrt {{p_{\rm{u}}}} \sum\limits_{i = 1}^K {\mathit{\boldsymbol{\hat f}}_k^{\rm{H}}} \Delta {\mathit{\boldsymbol{f}}_i}{x_i}}_{{\rm{信道估计误差信号}}} + \underbrace {\alpha \mathit{\boldsymbol{\hat f}}_k^{\rm{H}}\mathit{\boldsymbol{n}}}_{{\rm{AWGN}}} + \underbrace {\mathit{\boldsymbol{\hat f}}_k^{\rm{H}}{\mathit{\boldsymbol{n}}_q}}_{{\rm{量化噪声}}} \end{array} $ | (19) |
其中:fk为空间相关信道
同理,非理想CSI下第k个用户在大规模MIMO上行系统频谱效率近似结果如定理2所示.
定理2 在干扰机和空间相关信道场景下的低精度ADC大规模MIMO系统,若基站端采用MRC算法处理用户发送数据,则非理想CSI下第k个用户在大规模MIMO上行系统频谱效率可以近似为
| $ {{\hat R}_k} \approx {\rm{lb}}\left( {1 + \frac{{\alpha {p_{\rm{u}}}{\beta _k}\theta }}{{\alpha {p_{\rm{u}}}\lambda \sum\limits_{i = 1,i \ne k}^K {{\beta _i}} + \alpha {p_{\rm{u}}}\phi \sum\limits_{i = 1}^K {{\beta _i}} + v}}} \right) $ | (20) |
| $ v = (1 - \delta _{\rm{e}}^2)\left( {{\sigma ^2} + (1 - \alpha ){p_{\rm{u}}}\sum\limits_{i = 1}^K {{\beta _i}} + \kappa } \right)\sum\limits_{m = 1}^M | {r_{mm}}| $ |
| $ \begin{array}{*{20}{l}} {\theta = {{(1 - \delta _e^2)}^2}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^M {(|{r_{mn}}{|^2} + {r_{mm}}{r_{nn}})} } + } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{m \ne n}^M {\sum\limits_{n = 1}^M {{r_{mn}}} } {r_{nm}}} \right)} \end{array} $ |
| $ {\lambda = {{(1 - \delta _{\rm{e}}^2)}^2}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^M | } {r_{mn}}{|^2}} $ |
| $ {\phi = \delta _{\rm{e}}^2(1 - \delta _{\rm{e}}^2)\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^M | } {r_{mn}}{|^2}} $ |
在干扰机和空间相关信道场景下,采用频谱效率来评估大规模MIMO上行系统性能,其参数如表 1所示[7-8].大尺度衰落系数
|
|
表 1 仿真参数表 |
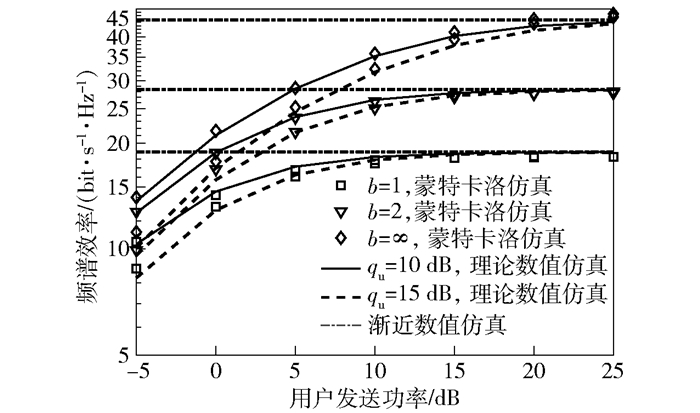
图 1给出了不同ADC量化精度和干扰机信号发送功率条件下,频谱效率与用户发送功率的关系.
|
图 1 频谱效率与用户发送功率的曲线变化趋势(K=10,M=100,γ=0.1) |
从图 1可知,定理1给出的频谱效率理论数值与蒙特卡洛仿真值具有较好的仿真效果.当用户发送功率较小(pu≤15dB)时,干扰机对系统的影响较大,并随干扰机发送功率的增加,频谱效率出现大幅度损失;当用户发送功率较大(pu>15dB)时,干扰机对系统的影响可以忽略不计,此时随着用户发送功率的增加,频谱效率出现饱和效应,这与推论1的理论分析结果一致.此外,在用户发送功率增加过程中,通过适当地增加ADC量化精度,可以显著提升系统性能.因此,需要尽可能调整pu>qu,同时适当地提高ADC量化精度,这样就可以提升系统整体频谱效率性能.
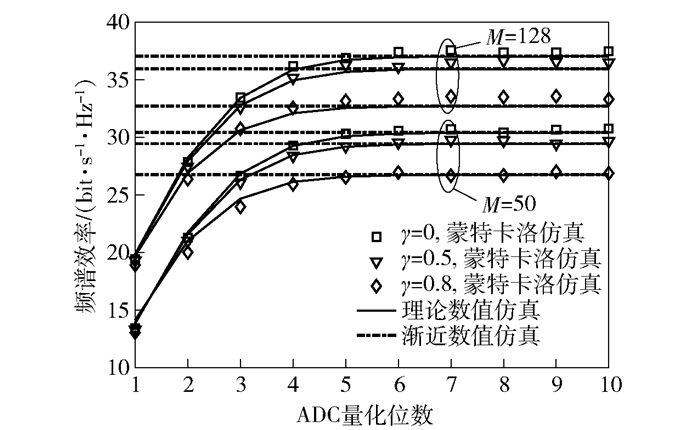
图 2给出了不同空间相关系数和基站天线数条件下,频谱效率与ADC量化精度的关系.从图 2可知,当ADC精度较低(b≤3)时,提高ADC精度能够快速提升频谱效率,此时改变空间相关系数γ对系统性能影响不大;当ADC精度较高(b>3)时,频谱效率出现饱和效应,此时再增大γ会使频谱效率出现大幅度损失,并且随着γ的增大而更加显著,这与推论2的理论分析结果一致.同时,随着M的增加,频谱效率得到明显地提升,但成倍数增加M并不能使系统性能得到同等倍数增加.这是由于基站的物理空间有限,部署大规模天线会使天线间距变窄,从而导致空间相关特性影响增大,进而影响系统整体性能.
|
图 2 频谱效率与ADC量化精度的曲线变化趋势(K=10,pu=qu=10dB) |
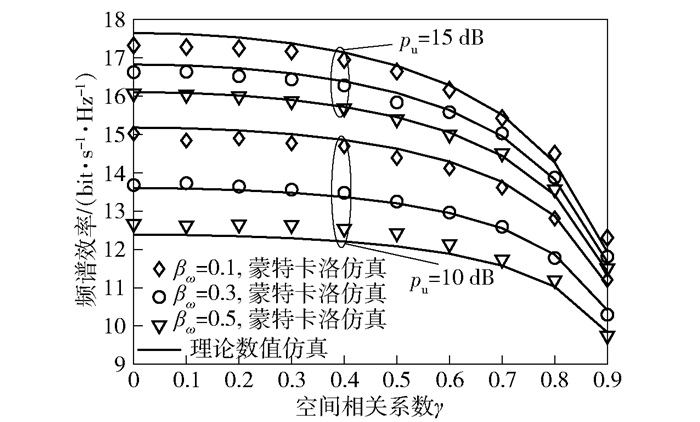
图 3给出了不同干扰机大尺度衰落系数和用户发送功率条件下,频谱效率与空间相关系数γ的关系.从图 3可知,当空间相关系数较小(γ≤0.5)时,增大γ对系统的性能几乎没有影响;当空间相关系数较大(γ>0.5)时,增大γ会使频谱效率快速下降,尤其在γ=0.8~0.9阶段呈现强相关性.此外,增大干扰机大尺度衰落系数也会使频谱效率出现大幅度的损失.但是,当空间相关系数固定时,通过适当地增大用户发送功率,频谱效率可以得到一定的补偿.
|
图 3 频谱效率与空间相关系数的曲线变化趋势(K=5,M=100,qu=10dB,b=1bit) |
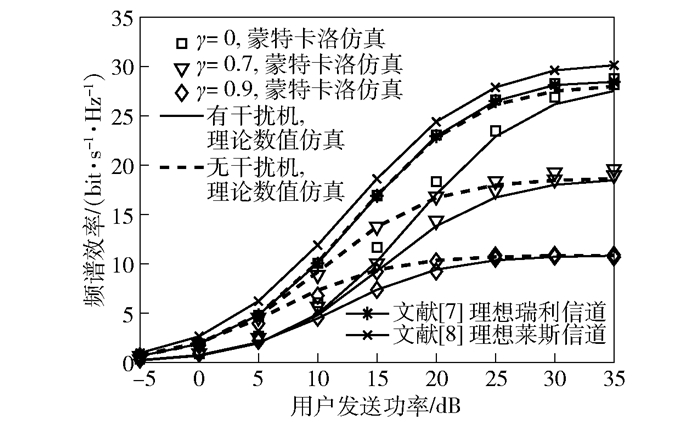
图 4给出了3种不同信道模型下,频谱效率与用户发送功率的关系.从图 4可知,在不考虑干扰机的情况下,当用户发送功率较低(pu≤5dB)时,3种信道下的频谱效率差距不大;随着用户发送功率进一步增大,频谱效率均达到了饱和状态,但莱斯信道的性能明显优于其他2种信道,而瑞利信道的性能介于莱斯信道和空间相关信道.当γ=0时,空间相关信道与瑞利信道的频谱效率曲线完全重合,这与推论3的理论分析结果一致.此外,在考虑干扰机和增大空间相关系数的情况下,频谱效率性能出现了大幅度下降.因此,为提升系统整体性能,在抑制干扰机干扰的同时,还需要尽可能地降低信道空间相关特性的影响.
|
图 4 3种信道下频谱效率与用户发送功率的曲线变化趋势(K=10,M=100,qu=10dB,b=2bit) |
图 5给出了不同CSI误差和干扰机大尺度衰落系数的条件下,频谱效率与基站天线数关系.从图 5可知,随着基站天线数的增加,频谱效率呈现逐渐增大趋势.但是,随着干扰机大尺度衰落系数的增大,频谱效率出现了明显的损失,因此充分考虑干扰机的大尺度衰落性能是完全有必要的.此外,随着CSI误差的减小,非理想CSI下的频谱效率性能逐渐接近理想CSI下的频谱效率.这是因为CSI误差越小,就能够充分保证空间相关信道的信道估计精度,从而提升系统的频谱效率性能.
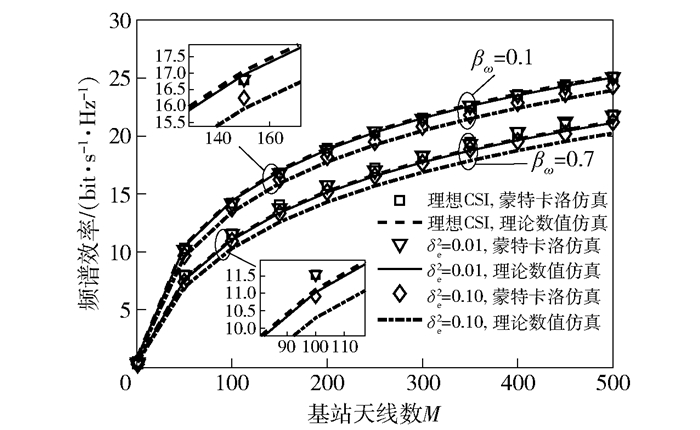
|
图 5 3种CSI下频谱效率与基站天线数的曲线变化趋势(K=5,pu=qu=10dB,γ=0.5,b=1bit) |
针对干扰机和空间相关信道场景下的多用户大规模MIMO上行系统,分析了低精度ADC、空间相关信道和干扰机对系统频谱效率的影响.首先,采用指数Toeplitz相关模型对信道建模;然后利用AQNM和MRC算法推导出频谱效率的近似表达式.基于得到的近似结果可知,当空间相关系数趋于零和ADC量化位数趋于无穷大时,意味着信道空间相关性和ADC量化误差给系统带来的影响可以忽略.在相同参数设置下,指出空间相关信道下的频谱效率均低于非相关的瑞利信道和莱斯信道下的频谱效率.仿真结果表明,当puqu时,干扰机对系统的影响占主导作用;当pu>qu时,能够有效地抑制干扰机对系统的影响.
| [1] |
金思年, 高鑫鑫, 岳殿武. 大规模MIMO上行系统中的等增益合并技术[J]. 北京邮电大学学报, 2017, 40(5): 50-54. Jin Sinian, Gao Xinxin, Yue Dianwu. Equal gain combining technique for massive MIMO uplink systems[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(5): 50-54. |
| [2] |
Özdogan Ö, Björnson E, Larsson E G. Massive MIMO with spatially correlated rician fading channels[J]. IEEE Transactions on Communications, 2019, 67(5): 3234-3250. DOI:10.1109/TCOMM.2019.2893221 |
| [3] |
Xu Weiye, Wen Benben, Lin Min, et al. Energy-efficient power allocation scheme for distributed antenna system over spatially correlated Rayleigh channels[J]. IET Communications, 2018, 12(5): 533-542. DOI:10.1049/iet-com.2017.0469 |
| [4] |
Alshammari A, Albdran S, Matin M. The effect of channel spatial correlation on capacity and energy efficiency of massive MIMO systems[C]//2017 IEEE 7th Annual Computing and Communication Workshop and Conference (CCWC). New York: IEEE Press, 2017: 1-5.
|
| [5] |
陶成, 郑文博, 李泳志, 等. 基于低精度量化的大规模MIMO-OFDM系统可达速率的研究[J]. 电子与信息学报, 2018, 40(10): 2294-2300. Tao Cheng, Zheng Wenbo, Li Yongzhi, et al. Achievable rate analysis on massive MIMO-OFDM systems with low-resolution ADC[J]. Journal of Electronics & Information Technology, 2018, 40(10): 2294-2300. |
| [6] |
Xu Liangyuan, Lu Xintong, Jin Shi, et al. On the uplink achievable rate of massive MIMO system with low-resolution ADC and RF impairments[J]. IEEE Communications Letters, 2019, 23(3): 502-505. DOI:10.1109/LCOMM.2019.2895823 |
| [7] |
Fan Li, Jin Shi, Wen Chaokai, et al. Uplink achievable rate for massive MIMO systems with low-resolution ADC[J]. IEEE Communications Letters, 2015, 19(12): 2186-2189. DOI:10.1109/LCOMM.2015.2494600 |
| [8] |
Zhang Jiayi, Dai Linglong, Sun Shengyang, et al. On the spectral efficiency of massive MIMO systems with low-resolution ADCs[J]. IEEE Communications Letters, 2016, 20(5): 842-845. DOI:10.1109/LCOMM.2016.2535132 |
| [9] |
Shiu D S, Foschini G J, Gans M J, et al. Fading correlation and its effect on the capacity of multielement antenna systems[J]. IEEE Transactions on Communications, 2000, 48(3): 502-513. DOI:10.1109/26.837052 |
| [10] |
Loyka S L. Channel capacity of MIMO architecture using the exponential correlation matrix[J]. IEEE Communications Letters, 2001, 5(9): 369-371. DOI:10.1109/4234.951380 |
| [11] |
Zhang Qi, Jin Shi, Wong Kai-kit, et al. Power scaling of uplink massive MIMO systems with arbitrary-rank channel means[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 966-981. DOI:10.1109/JSTSP.2014.2324534 |
| [12] |
Dong Peihao, Zhang Hua, Xu Wei, et al. Performance analysis of multiuser massive MIMO with spatially correlated channels using low-precision ADC[J]. IEEE Communications Letters, 2018, 22(1): 205-208. DOI:10.1109/LCOMM.2017.2761378 |



