提出一种缓存辅助边缘计算的卸载决策制定与资源优化方案,以进一步降低移动边缘计算(MEC)系统中终端设备的能量消耗.首先,建立该优化问题为最小化用户在任务执行时最坏情况下的能耗值,并将这一混合整数规划问题转化为非凸的二次约束二次规划(QCQP)模型,使用半定松弛及随机概率映射方法获得缓存辅助下的预选卸载集合;其次,分别采用拉格朗日对偶分解法和二分法求得性能约束下的最优传输功率及边缘计算资源分配,从而通过对比该集合中的设备能耗得到理想的卸载决策集合与资源分配方案.实验数值结果表明,所提方案能够有效降低用户能量消耗,提升边缘计算系统的服务性能.
An offloading decision and resource optimization scheme for cache-assisted edge computing is proposed to further reduce the energy consumption of terminal devices in the mobile egde computing(MEC)system.Firstly, the optimization problem is established to minimize the worst-case energy consumption of user during the task execution, and the mixed integer programming problem is transformed into a non-convex quadratic constrained quadratic programming(QCQP)model.Semidefinite-relaxation and randomization probability mapping are used to obtain the pre-selected offloading set assisted by caching; Secondly, the Lagrangian dual decomposition method and the bisection method are utilized to acquire the optimal transmission power and edge computing resource under constraints.By comparing the energy consumption of the set of devices, an ideal set of offloading decision and resource allocation scheme are got.Experiment shows that the proposed scheme can effectively reduce the energy consumption and improve the service performance of the edge computing system.
随着人工智能与物联网技术的迅速发展,更多的移动应用,如增强现实、虚拟游戏等任务密集型、延时敏感型应用数据对资源受限的用户设备提出了苛刻的要求[1].移动边缘计算(MEC,mobile egde computing)技术通过将高复杂度、高能耗计算任务卸载到靠近用户的移动网络边缘,可以提供分布式计算功能和本地化云服务.为满足未来5G网络计算任务大、热点内容集中、低时延低功耗等新兴业务的应用目标,部署缓存可以进一步降低基站负载和骨干网络压力,同时降低传输时延与设备能耗.因而,研究边缘网络部署缓存,减少用户能量消耗具有较大的科学意义与实际价值.
Zhang等[2]提出了一种能量感知的计算卸载方案,构建以设备能量寿命与延迟敏感型任务卸载的联合优化问题. Yang等[3]联合优化卸载任务比重、移动设备的发射功率和计算速率,来解决智能移动设备中的能量消耗问题. Guo等[4]提出多用户MEC系统有效能量分配模型,通过优化分配通信和计算资源,建立了能量消耗总加权和的最小化问题.张海波等[5]考虑系统总能耗,采用坐标下降法、基于改进的匈牙利算法与贪婪算法,来解决任务卸载和资源分配的联合优化问题.通过在MEC节点部署内容缓存可以有效提升能量利用率[6-8],Jia等[6]将边缘网络缓存资源分配问题描述为一个整数线性规划模型,提出了一种基于网络分片的缓存资源分配方案. Jiang等[7]研究蜂窝基站参与本地内容缓存的最优协作内容缓存和交付策略,有效减轻了回程负载以及用户能耗. Wang等[8]联合缓存策略和激励机制,依据共享存储资源来提高边缘网络效益,给出了一种启发式缓存策略.以上文献从不同侧面对MEC网络中的设备能耗进行了研究,但当考虑边缘节点部署内容缓存作为一种辅助执行能力并进行卸载机制研究时,上述理论将不再适用.因为任务执行选择的增多,单一寻优的处理策略易使得通过不同方式执行的公平度降低[9],降低资源利用率.
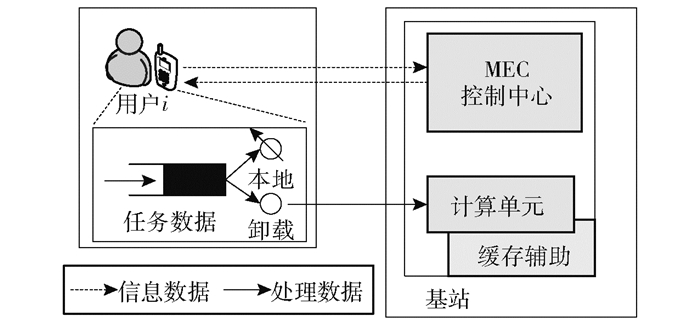
1 系统模型及问题提出 1.1 系统模型缓存辅助边缘计算的网络模型(见图 1)包括一个配备MEC服务单元的边缘基站和N个用户的集合{i=1,2,…,N}. MEC控制中心收到请求信息后分析并向用户回馈任务决策信息数据,使该用户设备能够按照既定的目标执行合理的决策.
|
图 1 系统模型 |
应用任务以参量Ai表示:Ai={Di, Ti},其中,Di表示该应用任务的数据大小,Ti表示执行此任务时所能容忍的最大延迟.此外,以ρi来表示任务数据的处理密度,即执行完成单位该任务时所需要的中央处理器(CPU, central processing unit)周期数.因而,完成一个应用任务所需的总CPU周期可表示为Ci=Diρi,在该文中,假定Di、Ci、ρi均为用户i的固有参量且为已知量.
在本地进行任务计算时,用户设备的计算资源表示为fil,本地执行功率为pil,则任务Ai在本地完成执行时,所需的时延及能量消耗可分别表示为
| $ {t_i^1 = \frac{{{C_i}}}{{f_i^1}}} $ | (1) |
| $ {e_i^1 = p_i^1\frac{{{C_i}}}{{f_i^1}}} $ | (2) |
当用户收到卸载信息数据时,需经无线链路将任务卸载到MEC计算单元进行计算处理. hi表示用户到边缘基站间的信道增益,σ2表示噪声功率,此时任务数据卸载上传的速率为
| $ {r_i} = W{\rm{lb}}\left( {1 + \frac{{p_i^m{h_i}}}{{{\sigma ^2}}}} \right) $ | (3) |
其中:W为系统带宽,pim为传输功率,最大值pimax.
将分配给用户i的计算资源表示为fimec,最大值为Fm.任务在边缘处理中,用户处于空闲状态且其空闲功率消耗为pic.则通过卸载方式执行任务时,时间消耗包括任务传输和任务执行时间2部分,有
| $ t_i^{{{\rm{m}}^\prime }} = \frac{{{D_i}}}{{{r_i}}} + \frac{{{C_i}}}{{f_i^{{{\rm{m}}^\prime }}}} $ | (4) |
因此用户设备的能量消耗可表示为
| $ e_i^{{{\rm{m}}^\prime }} = p_i^{\rm{m}}\frac{{{D_i}}}{{{r_i}}} + p_i^{\rm{c}}\frac{{{C_i}}}{{f_i^{{{\rm{m}}^\prime }}}} $ | (5) |
通过部署缓存资源,用以缓存已处理完成的应用任务或相关的原始数据,当用户请求的卸载任务已经缓存在边缘网络时,就无需进行任务卸载,可以直接通过下行链路从基站处接收结果数据,从而减少卸载传输能耗.边缘缓存的内容放置与数据大小、内容流行度有关,表示缓存的最大数据量为Cd.当用户收到可缓存的信息时,将处理结果数据经链路传到用户.由于在进行缓存处理时所需要的执行时间较快,在时间上可近似等于边缘服务器的执行时长[5],因而,其时间与能量消耗可分别建立为
| $ {t_i^{\rm{c}} = \frac{{{C_i}}}{{f_i^{{{\rm{m}}^\prime }}}}} $ | (6) |
| $ {e_i^{\rm{c}} = p_i^{\rm{c}}\frac{{{C_i}}}{{f_i^{{{\rm{m}}^\prime }}}}} $ | (7) |
MEC控制中心决策为xil、xim、xic∈{0, 1},代表本地计算、边缘计算和边缘缓存变量,即当xil=1、xim=1、xic=1表示用户i的任务通过本地方式执行、边缘服务器执行以及可以通过边缘缓存来处理;反之有xil=0、xim=0、xic=0.因此,基于系统模型的描述,用户i处理任务的总能量消耗可表示为
| $ {e_i} = e_i^1x_i^1 + e_i^{{{\rm{m}}^\prime }}x_i^{\rm{m}} + e_i^{\rm{c}}x_i^{\rm{c}}, $ | (8) |
决策向量表示为xi=[xil, xim, xic]T、功率分配向量为pm=[p1m, p2m, …, pNm],计算资源为fm′=[f1m′, f2m′, …, fNm′].为避免较多的任务集中于条件较好的执行方式,造成拥塞现象,基于公平性考虑建立该能耗目标优化问题为最小化用户在最差执行下的消耗值,即
| $ {\mathop {{\rm{min}}}\limits_{\{ {\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{p}}^{{\rm{ m }}}},{\mathit{\boldsymbol{f}}^{{\rm{m}}\prime }}\} } \mathop {{\rm{max}}}\limits_{i \in N} {e_i}} $ | (9) |
| $ {{\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_i^1 + x_i^{\rm{m}} + x_i^{\rm{c}} = 1} $ | (9a) |
| $ {x_i^1,x_i^{\rm{m}},x_i^{\rm{c}} \in \{ 0,1\} } $ | (9b) |
| $ {p_i^{\rm{m}} \le p_i^{{\rm{max}}}} $ | (9c) |
| $ {\sum\limits_{i \in N} {{C_i}} \le {C_{\rm{d}}}} $ | (9d) |
| $ {\sum\limits_{i \in N} {f_i^{\rm{m}}} \le {F_{\rm{m}}}} $ | (9e) |
| $ {t_i^1x_i^1 + t_i^{{{\rm{m}}^\prime }}x_i^{\rm{m}} + t_i^{\rm{c}}x_i^{\rm{c}} \le {T_i}} $ | (9f) |
其中:式(9a)、式(9b)表示任务只能通过其中一种方式执行;式(9c)表示传输功率最大限制;式(9d)、式(9e)分别为缓存容量与计算资源约束;式(9f)表示执行延迟约束.
2 基于半定松弛的卸载决策制定针对式(9)中包含的min-max双层优化模型以及式(9b)中的0-1约束问题,首先引入松弛变量Ee,令
| $ x_i^{{\rm{(1,m,c)}}}(x_i^{{\rm{(1,m,c)}}} - 1) = 0 $ | (10) |
卸载决策与功率、计算资源分配有关,因而在进行资源分配优化之前,首先给出在缓存辅助限制及时延阈值下的预选卸载集合,即在进行卸载决策制定时不再考虑式(9c)、式(9e)等约束.由于整数约束式(10)中存在二次项使得松弛后的目标问题依然是非凸的,定义(4N+1)×1向量yi=[xil, xim, xic, di, Ee]T,则该双层优化问题可以整理成标准的QCQP模型:
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{y}} {({\mathit{\boldsymbol{b}}_0})^{\rm{T}}}{\mathit{\boldsymbol{y}}_i} $ | (11) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{y}}_i^{\rm{T}} {\rm{diag}} ({\mathit{\boldsymbol{e}}_j}){\mathit{\boldsymbol{y}}_i} - {({\mathit{\boldsymbol{e}}_j})^{\rm{T}}}{\mathit{\boldsymbol{y}}_i} = 0,j \in \{ 1,2,3\} $ | (11a) |
| $ {{{(\mathit{\boldsymbol{b}}_i^{{\rm{(1,m,c)}}})}^{\rm{T}}}{\mathit{\boldsymbol{y}}_i} = 1} $ | (11b) |
| $ {\sum\limits_{i = 1}^N {{{(\mathit{\boldsymbol{b}}_i^{\rm{c}})}^{\rm{T}}}} {\mathit{\boldsymbol{y}}_i} \le {C_{\rm{d}}}} $ | (11c) |
| $ {{{(\mathit{\boldsymbol{b}}_i^{\rm{t}})}^{\rm{T}}}{\mathit{\boldsymbol{y}}_i} \le {T_i}} $ | (11d) |
其中:式(11a)为式(10)的等价约束,ej表示大小为(4N+1)×1的单位向量,j∈{1, 2, 3};式(11b)为任务执行唯一性的等价约束;式(11c)为缓存资源最大限制的等价约束,式(11d)为时延阈值限制的等价约束以及
经半定松弛转化后可以得到一个相应的半定规划(SDP,semidefinite programming)问题,定义转化向量Z=ziziT,其中zi=[yiT, 1]T,并忽略rank(Zi)=1限制,可以得到SDP问题函数:
| $ {\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{Z}} {\rm{ tr}} ({\mathit{\boldsymbol{G}}_0}{\mathit{\boldsymbol{Z}}_i})} $ | (12) |
| $ { {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{tr}} ({\mathit{\boldsymbol{G}}_j}\mathit{\boldsymbol{Z}}) = 0,j \in \{ 1,2,3\} } $ | (12a) |
| $ { {\rm{tr}} (\mathit{\boldsymbol{G}}_i^s\mathit{\boldsymbol{Z}}) = 1,i \in N} $ | (12b) |
| $ { {\rm{tr}} (\mathit{\boldsymbol{G}}_i^c\mathit{\boldsymbol{Z}}) \le {C_{\rm{d}}},i \in N} $ | (12c) |
| $ { {\rm{tr}} (\mathit{\boldsymbol{G}}_i^t\mathit{\boldsymbol{Z}}) \le {T_i},i \in N} $ | (12d) |
| $ {\mathit{\boldsymbol{Z}}(4N + 2,4N + 2) = 1} $ | (12e) |
| $ {{\mathit{\boldsymbol{Z}}_i} \ge 0} $ | (12f) |
其中
| $ {\mathit{\boldsymbol{G}}_0} = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{(4N + 1) \times (4N + 1)}}}&{\frac{1}{2}{\mathit{\boldsymbol{b}}_0}}\\ {\frac{1}{2}{{({\mathit{\boldsymbol{b}}_0})}^{\rm{T}}}}&0 \end{array}} \right],{\mathit{\boldsymbol{G}}_j} = \left[ {\begin{array}{*{20}{c}} { {\rm{diag}} ({\mathit{\boldsymbol{e}}_j})}&{\frac{1}{2}{\mathit{\boldsymbol{e}}_j}}\\ { - \frac{1}{2}{{({\mathit{\boldsymbol{e}}_j})}^{\rm{T}}}}&0 \end{array}} \right], $ |
| $ \begin{array}{l} \mathit{\boldsymbol{G}}_i^s = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{(4N + 1) \times (4N + 1)}}}&{\frac{1}{2}\mathit{\boldsymbol{b}}_i^{{\rm{(1,m,c)}}}}\\ {\frac{1}{2}{{(\mathit{\boldsymbol{b}}_i^{{\rm{(1,m,c)}}})}^{\rm{T}}}}&0 \end{array}} \right],\quad \mathit{\boldsymbol{G}}_i^c = \\ \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{(4N + 1) \times (4N + 1)}}}&{\frac{1}{2}\mathit{\boldsymbol{b}}_i^{\rm{c}}}\\ {\frac{1}{2}{{(\mathit{\boldsymbol{b}}_i^{\rm{c}})}^{\rm{T}}}}&0 \end{array}} \right],\mathit{\boldsymbol{G}}_i^t = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{(4N + 1) \times (4N + 1)}}}&{\frac{1}{2}\mathit{\boldsymbol{b}}_i^t}\\ {\frac{1}{2}{{(\mathit{\boldsymbol{b}}_i^t)}^{\rm{T}}}}&0 \end{array}} \right] \end{array} $ |
将式(12)中优化解表示为Zi*,根据对向量的定义,所需的预选卸载决策即存在于Zi*中左顶角3N×3N的子矩阵中,表示为
| $ {s_i} = \{ {[1,0,0]^{\rm{T}}},{[0,1,0]^{\rm{T}}},{[0,0,1]^{\rm{T}}}\} $ | (13) |
获取了预选卸载决策后,进行资源分配优化的分析,包括传输功率分配及计算资源的分配.
3.1 用户传输功率分配整理目标函数式(9),将资源分配问题表示为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_{\{ {\mathit{\boldsymbol{p}}^{{\rm{ m }}}},{\mathit{\boldsymbol{f}}^{i \in {\rm{m}}\prime }}\} } \mathop {{\rm{max}}}\limits_{i \in N} \\ \left[ {p_i^1\frac{{{C_i}}}{{f_i^1}}x_i^l + p_i^{\rm{m}}\frac{{{D_i}}}{{{r_i}}}x_i^{\rm{m}} + p_i^{{\rm{id}}}\frac{{{C_i}}}{{f_i^{{{\rm{m}}^\prime }}}}(x_i^{\rm{m}} + x_i^{\rm{c}})} \right] \end{array} $ | (14) |
| $ {{\rm{s}}{\rm{. t}}{\rm{. }}p_i^{\rm{m}} \le p_i^{{\rm{max}}}} $ | (14a) |
| $ {\sum\limits_{i \in N} {f_i^{{{\rm{m}}^\prime }}} \le {F_{\rm{m}}}} $ | (14b) |
由于计算资源分配与功率分配在目标函数式和约束中均是非耦合的,所以假定其计算资源已经给定,整理式(14)可将用户功率分配目标函数重写为
| $ \begin{array}{l} {\rm{ }}\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{p}}^{\rm{m}}}} \mathop {{\rm{max}}}\limits_{i \in {N_1}} \frac{{p_i^{\rm{m}}{D_i}}}{{W{\rm{lb}} \left( {1 + \frac{{p_i^{\rm{m}}{h_i}}}{{{\sigma ^2}}}} \right)}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le p_i^{\rm{m}} \le p_i^{{{\rm{m}}^\prime }} \end{array} $ | (15) |
其中N1代表所有通过卸载传输执行的用户.对于该双层非凸问题进行转化,定义目标式(15)的最优功率分配与其最优解为pm*、V*,可以得到
| $ \begin{array}{l} {V^*} = \mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{p}}^{\rm{m}}}} \mathop {{\rm{max}}}\limits_{i \in {N_1}} \frac{{p_i^{\rm{m}}{D_i}}}{{W{\rm{lb}} \left( {1 + \frac{{p_i^{\rm{m}}{h_i}}}{{{\sigma ^2}}}} \right)}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{max}}}\limits_{i \in {N_1}} \frac{{p_i^{{{\rm{m}}^*}}{D_i}}}{{W{\rm{lb}}\left( {1 + \frac{{p_i^{{{\rm{m}}^*}}{h_i}}}{{{\sigma ^2}}}} \right)}} \end{array} $ | (16) |
根据非线性分数规划理论,当且仅当有
| $ {\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{p}}^{\rm{m}}},{E_p}} {E_p}} $ | (17) |
| $ {{\rm{ s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le p_i^{\rm{m}} \le p_i^{{\rm{max}}}} $ | (17a) |
| $ {p_i^{\rm{m}}{D_i} - VW {\rm{lb}} \left( {1 + \frac{{p_i^{\rm{m}}{h_i}}}{{{\sigma ^2}}}} \right) \le {E_p}} $ | (17b) |
对于式(17)的混合凸优化,可以通过拉格朗日对偶分解算法从目标函数中分解出优化变量,从而获得最优功率分配pim*,即构造拉格朗日函数为
| $ \begin{array}{*{20}{c}} {L(p,{E_p},\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}) = }\\ {{E_p} + \sum\limits_{i \in {N_1}} {{\alpha _i}} (p_i^{\rm{m}} - p_i^{{\rm{max}}}) + }\\ {\sum\limits_{i \in {N_1}} {{\beta _i}} \left[ {p_i^{\rm{m}}{D_i} - VW{\rm{lb}}\left( {1 + \frac{{p_i^{\rm{m}}{h_i}}}{{{\sigma ^2}}}} \right) - {E_p}} \right]} \end{array} $ | (18) |
其中α=[α1, α2, …, αN1]≥0、β=[β1, β2, …, βN1]≥0为拉格朗日乘子.由于该凸优化函数使得零对偶间隙得以保证,强对偶性成立,表示其对偶函数有
| $ D(\mathit{\boldsymbol{\alpha ,\beta }}) = \mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{p}}^{\rm{m}}},{E_p}} L(p,{E_p},\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}) $ | (19) |
则分解后的功率分配函数式为
| $ \mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{p}}^m}} \left\{ {\sum\limits_{i \in {N_1}} {{\alpha _i}} p_i^{\rm{m}} + \sum\limits_{i \in {N_1}} {{\beta _i}} \left[ {p_i^{\rm{m}}{D_i} - VW{\rm{lb}}\left( {1 + \frac{{p_i^{\rm{m}}{h_i}}}{{{\sigma ^2}}}} \right)} \right]} \right\} $ | (20) |
经卡罗需-库恩-塔克(KKT, Karush-Kuhn-Tucker)条件可以得到最优的功率分配解析式为
| $ p_i^{{{\rm{m}}^*}} = {\left[ {\frac{{VW{\beta _i}}}{{{\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2({\alpha _i} + {\beta _i}{D_i})}} - \frac{{{\sigma ^2}}}{{{h_i}}}} \right]^ + } $ | (21) |
获得传输功率后,继续对边缘端的计算资源进行分配.整理式(14),可以得到优化问题为
| $ \mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{f}}^{{{\rm{m}}^\prime }}}} \mathop {{\rm{max}}}\limits_{i \in {N_2}} \left( {\frac{{p_i^{{\rm{id}}}{C_i}}}{{f_i^{{{\rm{m}}^\prime }}}} + {F_i}} \right) $ | (22) |
| $ {{\rm{ s}}{\rm{. t}}{\rm{. }}f_i^{{{\rm{m}}^\prime }} \ge 0} $ | (22a) |
| $ {\sum\limits_{i \in {N_2}} {f_i^{{{\rm{m}}^\prime }}} \le {F_{\rm{m}}}} $ | (22b) |
其中:N2代表在边缘计算单元执行任务的用户,常量
| $ {\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{f}}^{{{\rm{m}}^\prime }}},{E_f}} {E_f}} $ | (23) |
| $ {{\rm{ s}}{\rm{.t}}{\rm{. }}{\kern 1pt} f_i^{{{\rm{m}}^\prime }} \ge 0} $ | (23a) |
| $ {\frac{{p_i^{{\rm{id}}}{C_i}}}{{f_i^{{{\rm{m}}^\prime }}}} + {F_i} \le {E_f}} $ | (23b) |
对于式(23)优化问题,可以通过将其转化为拟凸问题优化模型,并通过二分法求得其最优值fim*.
综上,当求得最优的pim*、fim*时,通过在每一次预选卸载决策下,计算消耗的能量,从而给出理想的卸载决策.具体算法实现过程流程如下.
步骤1 利用Matlab凸优化工具CVX解决式(12)的SDP问题,获得最优解;
步骤2 记录通过随机概率映射获得的预选卸载集合,并依式(21)完成用户功率分配,及对应的计算资源分配;
步骤3 计算在每一次预选卸载决策下,完成资源分配时的设备能量消耗;
步骤4 选择计算得到的能耗最小值,输出最小值对应的最终卸载决策与资源分配量.
4 仿真分析仿真MEC网络场景包括1个边缘基站和12个用户设备,用户随机分布在[200m,200m].考虑本地CPU工作频率为1G cycle/s,最大发送功率0.8W,设备与基站之间的传输带宽为15MHz,噪声功率与信道增益分别为σ2=2×10-13和hi=127+30×lbd,d为传输距离.假定边缘最大计算能力为35G cycle/s;设备空闲功率0.01W,任务数据量大小0.42MB及任务处理密度297.62cycle/bit[9].对于缓存内容数据设定,考虑边缘缓存辅助的最大容量为120MB,且其缓存的内容服从Zipf分布[6, 8, 11].对比中,选取具有相同缓存场景的文献[11]进行分析,该文中针对平均能耗最小化模型提出了一种低复杂度的次优算法.
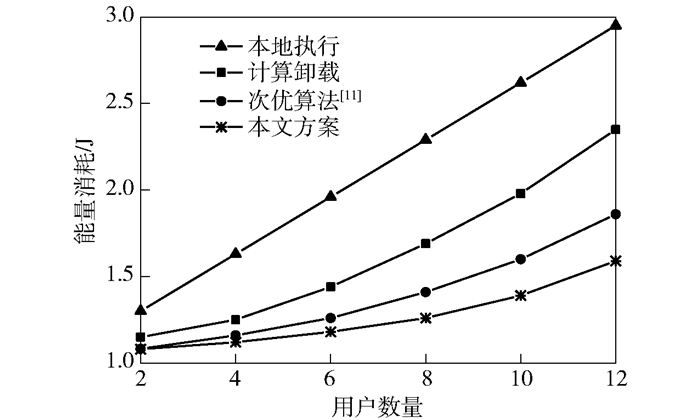
图 2所示为在不同用户数量下终端设备能量消耗的变化曲线,示出了所提方案与任务通过本地执行、联合计算卸载方式执行以及Cui等[11]提出的低复杂度次优算法进行对比的结果.其中,本地计算时功率为pim=0.4W;应用容忍时延Ti=5s及缓存容量Cd=120MB.从图中可以看出,随着用户数目的增长,其能量消耗均几近线性地增加,并且具有缓存处理能力的MEC网络能够有效地降低设备能耗,而本文所提方案具有最低的能耗,并且随着用户数目的增大这一趋势更加明显,体现出了较好的系统性能.
|
图 2 不同用户数量下设备能量消耗的变化曲线 |
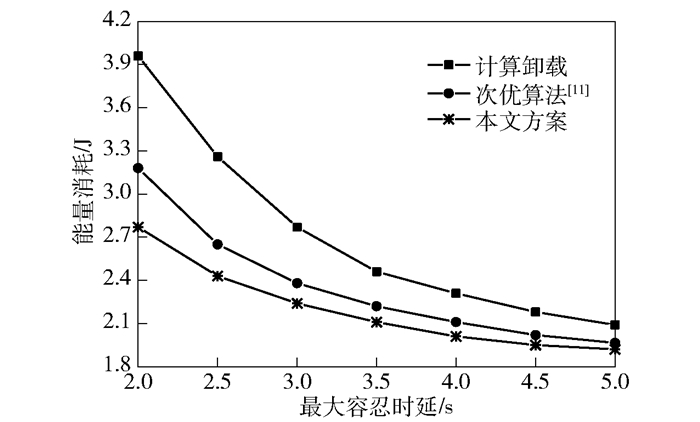
图 3所示为不同不应用容忍时延下用户能量消耗的变化,其中:N=12,Cd=120MB.从图中可见,任务最大容忍时延与用户能耗有着密切的关系,在该时延阈值增大时,更多的应用任务可以选择通过卸载计算或者缓存来处理,使得用户消耗较小的能量;其次,具有缓存能力的MEC系统增加了任务处理选择,同样拥有更少的能量消耗.相较于另外2种方案,所提方案在容忍延迟体现较为苛刻时,其用户能量消耗增加幅度更小,可以更好地满足低功耗、低时延应用任务需求.
|
图 3 最大容忍时延对用户能量消耗的影响 |
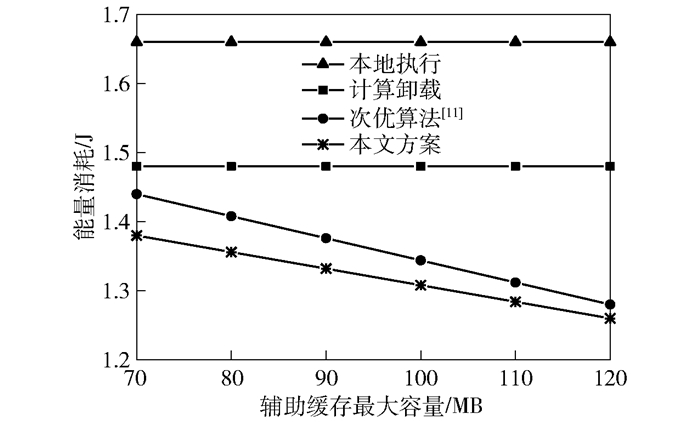
图 4给出了边缘缓存的最大能力对用户能量消耗的影响曲线.当数据任务在用户本地处理或通过无缓存能力的计算卸载方式执行时,缓存辅助能力不会对该能耗产生影响.采用如Cui等[11]的缓存内容放置方式,固定偏斜系数为γ=1的内容服务流行度,即可以准确缓存用户所需内容的程度.可以看出,当给定的缓存容量值增大时,可以显著减少其用户的能量消耗.与对比算法相比,所提方案能够减少能耗5.6%以上,当其容量值较大时,这一优势变小,这是由于本文模型考虑了用户卸载选择的公平性,在一定程度上折中了能耗.
|
图 4 辅助缓存最大容量对用户能量消耗的影响 |
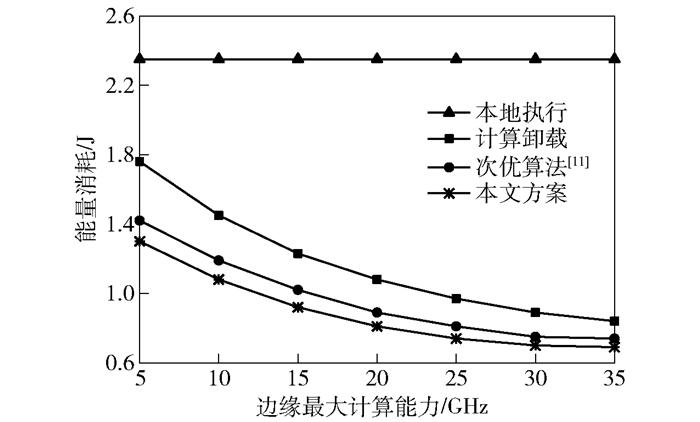
图 5给出了当N=12,Rc=120MB时,边缘最大计算能力对用户能量消耗的影响.可以看出,除了在本地执行外,边缘计算单元能力的大小可影响MEC系统用户设备的能耗,该能耗值随边缘计算能力的增大而逐渐降低,与仅存在计算执行能力的系统方案有所不同,具有缓存辅助能力的MEC系统用户,其能量消耗对边缘计算能力大小的依赖相对较小,且相较于对比算法与另外2种传统执行方式,所提方案在测试范围内均具有最低的能量消耗,表现出了较好的资源优化性能.
|
图 5 边缘最大计算能力对用户能量消耗的影响曲线 |
面向MEC网络提出一种在缓存辅助下的卸载决策与资源优化方案.通过半定松弛方法对所提联合优化目标函数进行了标准化构造,给出预选卸载策略集合,并根据拉格朗日对偶分解方法得到最优的用户传输功率,以及采用二分法对边缘计算资源进行优化分配.仿真分析了缓存辅助能力、边缘计算能力等因素对系统能耗的影响,对比相同场景的已有方案,其能耗最大可减少18.6%,表明所提方案在兼顾系统公平性的同时有效降低了MEC终端设备的能量消耗.
| [1] |
田辉, 范绍帅, 吕昕晨, 等. 面向5G需求的移动边缘计算[J]. 北京邮电大学学报, 2017, 40(2): 1-10. Tian Hui, Fan Shaoshuai, Lu Xinchen, et al. Mobile edge computing for 5G requirements[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(2): 1-10. |
| [2] |
Zhang Jiao, Hu Xiping, Ning Zhaolong, et al. Energy-latency tradeoff for energy-aware offloading in mobile edge computing networks[J]. IEEE Internet of Things Journal, 2017, 5(4): 2633-2645. |
| [3] |
Yang Lichao, Zhang Heli, Li Ming, et al. Mobile edge computing empowered energy efficient task offloading in 5G[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 6398-6409. DOI:10.1109/TVT.2018.2799620 |
| [4] |
Guo Junfeng, Song Zhaozhe, Cui Ying, et al. Energy-efficient resource allocation for multi-user mobile edge computing[C]//IEEE Global Communications Conference (GLOBECOM). Singapore: IEEE Press, 2017: 1-7.
|
| [5] |
张海波, 李虎, 陈善学, 等. 超密集网络中基于移动边缘计算的任务卸载和资源优化[J]. 电子与信息学报, 2019, 41(5): 1194-1201. Zhang Haibo, Li Hu, Chen Shanxue, et al. Computing offloading and resource optimization in ultra-dense networks with mobile edge computation[J]. Journal of Electronics and Information, 2019, 41(5): 1194-1201. |
| [6] |
Jia Qingming, Xie Renchao, Tao Huang, et al. Efficient caching resource allocation for network slicing in 5G core network[J]. IET Communications, 2017, 11(18): 2792-2799. DOI:10.1049/iet-com.2017.0539 |
| [7] |
Jiang Wei, Feng Gang, Qin Shuang. Optimal cooperative content caching and delivery policy for heterogeneous cellular networks[J]. IEEE Transactions on Mobile Computing, 2016, 16(5): 1382-1393. |
| [8] |
Wang Shuo, Zhang Xin, Wang Lin, et al. Joint design of device to device caching strategy and incentive scheme in mobile edge networks[J]. IET Communications, 2018, 12(14): 1728-1736. DOI:10.1049/iet-com.2017.1044 |
| [9] |
Du Jianbo, Zhao Liqiang, Feng Jie, et al. Computation offloading and resource allocation in mixed fog/cloud computing systems with min-max fairness guarantee[J]. IEEE Transactions on Communications, 2018, 66(4): 1594-1608. DOI:10.1109/TCOMM.2017.2787700 |
| [10] |
Chen Meng-HSi, Dong Min, Liang Ben. Resource sharing of a computing access point for multi-user mobile cloud offloading with delay constraints[J]. IEEE Transactions on Mobile Computing, 2018, 17(12): 2868-2881. DOI:10.1109/TMC.2018.2815533 |
| [11] |
Cui Ying, He Wen, Ni Chun, et al. Energy-efficient resource allocation for cache-assisted mobile edge computing[C]//2017 IEEE 42nd Conference on Local Computer Networks (LCN). Singapore: IEEE Press, 2017: 640-664.
|


