针对毫微微基站(FBS)在不同时间段用户数量的差异,研究了最大化下行总信息量的功率分配问题.不同时间段包含忙时和闲时2个阶段,忙时用户数量较多,闲时用户数量较少.通过部署一个无人机携带的微微基站(PBS-UAV)为多个FBSs闲时的用户提供服务.FBS和PBS-UAV都具有能量收集功能.在FBS忙时,FBS和PBS-UAV同时从宏基站收集能量,并且向用户发送数据.FBS闲时,由PBS-UAV接替多个FBSs,与用户进行下行通信.将功率分配问题建模为最优化问题,以最大化FBS和PBS-UAV的下行信息量为目标,同时满足FBS和PBS-UAV能量消耗及发射功率的约束条件.由于建立的最优化问题是凸优化问题,可通过引入增广拉格朗日乘子法获得最优解.仿真结果表明,与PBS-UAV参与的等功率及部分功率固定的方法相比,所提出的方法在总信息量方面有不同程度的增加.
Aiming at the difference of users in different time periods for the femto base station (FBS), the power allocation problem of maximizing the total downlink information is investigated.The different time periods include busy time and spare time.There are more users in the busy time and less users in the spare time.By deploying a pico base station carried by unmanned aerial vehicle (PBS-UAV), it provides services for users of multiple FBSs in spare time.Both the FBS and PBS-UAV have energy harvesting function.During the busy time, the FBS and PBS-UAV simultaneously harvest energy from the macro base station, and FBSs transmit data to users.During the spare time, multiple FBSs are replaced by the PBS-UAV to communicate with users in downlink.The power allocation problem is modeled as an optimization problem.The objective is to maximize the amount of downlink information of FBSs and PBS-UAV while satisfying the constraints of FBS and PBS-UAV energy consumption and transmission power.Because the formulated optimization problem is a convex optimization problem, the optimal solution is obtained by using an augmented Lagrange multiplier method.Simulations show that compared with the equal power method and partial fixed power method with PBS-UAV, the proposed method has an increase in terms of total information to different degrees.
射频能量收集是一种可以持续从环境电磁波收集能量的技术.通信设备通过从环境电磁波收集能量获得电能,是一种新兴的绿色环保供电方式[1-2].然而,这种供电方式存在着收集到的能量相对较少的缺点.因此,为了充分利用有限的能量,研究射频能量收集通信系统的资源分配问题,对于提升通信系统的性能具有重要意义.
能量收集通信系统的资源分配问题已经吸引了极大的研究兴趣. Zhao等[3]在具有环境射频能量收集功能的蜂窝网络中,研究上行资源分配的问题,在满足能耗和数据速率要求的同时,最大化能量效率. Guo等[4]在移动无线传感器网络中,中继节点通过从发射机接收射频信号来获取能量,收集到的能量用于补偿中继节点数据转发所消耗的能量,从而实现能量效率最大化. Luo等[5]在具有能量收集功能的设备到设备(D2D,device-to-device)的蜂窝网络中,由收集的能量驱动的D2D设备可以复用蜂窝用户占用的频谱资源,在系统可用能量和服务质量的约束下,最大化蜂窝网络的总速率. Lohani等[6]在具有能量收集功能的异构无线网络中,通过研究热点小区中微微基站的动态激活和功率分配来提高用户的平均吞吐量. Wang等[7]利用无人机(UAV,unmanned aerial vehicle)作为射频源,为一组传输大量信息的D2D设备提供能量,该D2D设备具有射频能量收集功能,在满足D2D设备能耗的情况下,最大化一个周期内的平均吞吐量. Yang等[8]在城市通信环境中,针对具有能量收集功能的UAV中继系统,研究UAV和地面接收端之间的信道衰落,并对不同城市环境参数下的中断概率进行分析. Xie等[9]在无线能量通信网络中,将UAV作为无线接入点,使用射频能量传输为用户充电,用户使用收集到的能量独立向UAV发送信息,UAV飞行速度受到最大飞行速度的约束,用户上行无线信息传输消耗的能量小于用户从UAV下行能量传输收集到的能量,以最大化所有地面用户的上行吞吐量为目标. Pan等[10]在UAV作为次级用户的认知无线电网络中,次级用户需要通过频谱感知来确定是否传输数据,对感知时间和次级传输功率进行了联合优化,提高了认知无线电系统的能量效率. Hua等[11]针对终端设备数据量大的问题,引入UAV作为飞行基站处理终端设备迁移来的任务,通过对UAV的功率、飞行轨迹以及终端的功率等进行联合优化,以减少终端的能量消耗. Zhu等[12]在同步无线信息和功率传输系统中,针对不完全的信道状态信息,提出鲁棒的安全波束成形方案,在受到用户保密率中断概率和能量收集器收集能量中断概率的约束下,最小化发射功率. Chu等[13]研究多输入单输出保密信道的同步无线信息和功率传输,设计出无人工噪声波束形成传输策略,受到发射功率和能量收集的限制,最大化传输保密率. Chu等[14]研究了一种全双工自能量回收的安全无线供电综合服务系统,通过联合考虑能量波束成形、组播服务、保密单播服务和人造噪声,设计最优输入协方差矩阵,使保密组播速率区域(SMRR,secrecy-multicast rate region)在传输功率约束下达到最大化.受Lohani等[6]热点小区中的微微基站的动态激活的启发,如果在热点区域部署一些毫微微基站(FBS,femto base station),它们拥有类似动态激活的功能,让其在繁忙时间工作,空闲时间停止通信.相比让这些FBSs一直持续工作,能够显著减少能量消耗.然而,FBSs在闲时仍然具有少量用户.如何保证在FBSs停止通信时仍能够为这些少量用户提供服务,是亟待解决的问题.传统的解决方法是将FBSs用户转移到宏基站(MBS,macro base station),但MBS的通信资源通常比较紧张,并且FBSs用户距离MBS相对较远,会导致被转移的FBSs用户吞吐量下降.受UAV参与组网的启发,如果让UAV携带微微基站,在FBSs停止通信时,由UAV携带的微微基站(PBS-UAV,pico base station carried by UAV)接替FBS,就可以为部分FBS用户提供可靠的服务.
针对FBSs忙时用户数量较多和闲时用户数量较少的特点,提出一种UAV协助的分时段最大化下行总信息量的功率分配策略.通过引入一个具有能量收集功能的PBS-UAV,在用户数量较多的情况下,多个FBSs工作.在闲时用户数量较少的情况下,由一个PBS-UAV接替多个FBSs工作.相比让多个FBSs在闲时一直持续工作,由一个PBS-UAV接替多个FBSs工作能够显著减少能量消耗.在FBSs忙时,FBSs和PBS-UAV都从MBS收集能量,并且FBSs与用户进行下行通信.在FBS闲时,FBSs停止与用户通信,由PBS-UAV为多个FBSs用户提供通信服务.此时,PBS-UAV距离FBSs较近,从FBSs收集能量,可以充分利用FBSs的剩余能量.同时,PBS-UAV距离MBS相对较远(不同于FBSs忙时的情况,PBS-UAV可以飞行到距离MBS较近的位置,进行能量收集),没有考虑从MBS收集能量.将功率分配问题建立成一个最优化问题,以最大化下行总信息量为目标,同时满足PBS-UAV和FBS的能量消耗和发射功率的约束条件.该最优化问题为一个凸优化问题,通过采用增广拉格朗日乘子法获得最优解.最后,通过仿真对提出的功率分配策略进行性能评估.
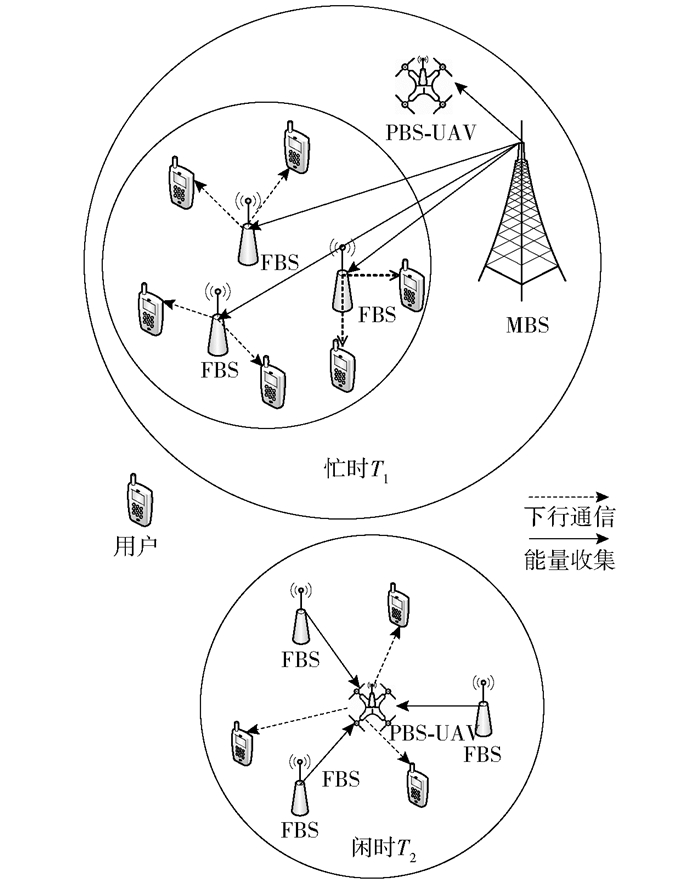
1 系统模型 1.1 网络结构分时段网络结构(见图 1)分为忙时T1和闲时T2两个阶段,假设有1个MBS、1个PBS-UAV和N个FBSs.在忙时T1时间段内,FBSs和PBS-UAV同时从MBS收集能量,FBS工作并向用户发送下行数据,PBS-UAV仅仅收集储存能量.在闲时T2时间段内,PBS-UAV以自身覆盖范围更大的优势接替FBSs,并向用户发送下行数据.同时,FBSs将T1阶段的剩余能量以一定的转化率转移给PBS-UAV,用于完成T2阶段的通信任务.
|
图 1 分时段网络结构 |
需要注意,通信过程包括下行和上行2个阶段.在下行通信阶段,FBSs和PBS-UAV向用户发送信号,会消耗一定的能量.在上行通信阶段,FBSs和PBS-UAV接收用户的信号,也会消耗一定的能量.由于笔者考虑的是下行总信息量最大化,在网络结构图中只画出了FBS和PBS-UAV的下行通信链路,但能量消耗也包括上行通信的能量消耗.
1.2 基站能量收集和消耗模型假设一个完整的工作周期为T,分为忙时T1和闲时T2两个阶段,忙时T1阶段用户数量多,闲时T2阶段用户数量少. T1阶段多个FBSs和PBS-UAV分别从MBS收集能量,MBS的发射功率为PM1.
考虑1个FBS在T1时间段内从MBS收集到的能量为[1]
| $ {E_{{\rm{F1}}}} = {T_1}\eta {P_{{\rm{M1}}}}|{G_{{\rm{MF}}}}{|^2} $ | (1) |
其中:η为FBS从MBS接收能量时的能量转换效率,GMF为MBS到FBS的信道增益.
在T1时间段内,PBS-UAV飞行到适宜区域进行能量收集,收集到的能量减去飞行所消耗的能量,剩余存储的能量为
| $ \begin{array}{*{20}{c}} {{E_{{\rm{P1}}}} = {E_{{\rm{U0}}}} + \zeta \gamma {T_1}{P_{{\rm{M1}}}}|{G_{{\rm{MP}}}}{|^2} - }\\ {(1 - \gamma ){T_1}{P_{{\rm{UF}}}} - \gamma {T_1}{P_{{\rm{UH}}}}} \end{array} $ | (2) |
其中:EU0为PBS-UAV的初始能量,ζ为PBS-UAV携带的能量收集器从MBS收集能量的能量转化效率,γ为PBS-UAV收集能量的时间比例,GMP为MBS到PBS-UAV的信道增益,1-γ为PBS-UAV飞行的时间比例,PUF为PBS-UAV飞行过程中消耗的功率,PUH为PBS-UAV悬停过程中消耗的功率,悬停时间等于收集能量的时间.
此外,FBS收集能量的同时向用户发送信息.考虑FBS的电路、发射信号和接收信号的能量消耗,得到1个FBS的能量消耗为
| $ {E_{\rm{F}}} = \sum\limits_i^I {P_i^{{\rm{FT}}}} \mu {T_1} + {P_{{\rm{FR}}}}(1 - \mu ){T_1} + {P_{{\rm{CF}}}}{T_1} $ | (3) |
其中:I为1个FBS覆盖范围下的用户数量,PiFT为FBS到第i(i=1, 2, …, I)个用户的发射功率,μ为FBS在T1内下行发送信号的时间比例,1-μ为FBS在T1内接收信号的时间比例,PFR是FBS接收信号的功率消耗,PCF为FBS电路的功率消耗.
对于PBS-UAV,在T2时间段内开始向用户发送下行数据,考虑PBS-UAV的电路、发射信号和接收信号的能量消耗,得到1个PBS-UAV的能量消耗为
| $ {E_{\rm{P}}} = \sum\limits_{j = 1}^J {P_j^{{\rm{PT}}}} \xi {T_2} + {P_{{\rm{PR}}}}(1 - \xi ){T_2} + {P_{{\rm{CP}}}}{T_2} $ | (4) |
其中:J为PBS-UAV覆盖范围下的用户数量,PjPT为PBS-UAV到第j(j=1, 2, …, J)个用户的发射功率,ξ为T2时间段内PBS-UAV下行发送信号的时间比例,1-ξ为T2时间段内PBS-UAV接收信号的时间比例,PPR为PBS-UAV接收信号的功率消耗,PCP为PBS-UAV电路的功率消耗.
2 问题建模和求解 2.1 问题建模针对第1节的系统模型,提出一种下行总信息量最大化的功率分配策略.假设N个FBSs覆盖范围内的用户数量、N个FBSs与MBS的距离都一致,从而简化下行吞吐量公式的复杂度.在FBSs数量、位置以及用户数量位置不一致的情况下,位置的改变会导致FBS到用户的信道增益和噪声功率产生变化,该变化最终会对最后的求解结果造成影响,但对问题本身的建模不会造成影响.仅在理想的情况,考虑其中一个FBS即可.可以得到在T1时间段内1个FBS的下行总吞吐量为
| $ {R_{\rm{F}}} = \sum\limits_{i = 1}^I {{B_1}} {\rm{lb}}\left( {1 + \frac{{P_i^{{\rm{FT}}}|G_i^{{\rm{FU}}}{|^2}}}{{{N_0}}}} \right) $ | (5) |
其中:B1为信道带宽,GiFU为FBS到第i(i=1, 2, …, I)个用户的信道增益,N0为噪声功率.
在T2阶段,PBS-UAV接替FBS工作.该阶段用户数量较少,PBS-UAV覆盖N个FBSs的工作区域,完成和用户间的通信.在T2阶段,PBS-UAV到用户的下行总吞吐量为
| $ {R_{\rm{P}}} = \sum\limits_{j = 1}^J {{B_2}} {\rm{lb}} \left( {1 + \frac{{P_j^{{\rm{PT}}}|G_j^{{\rm{PU}}}{|^2}}}{{{N_1}}}} \right) $ | (6) |
其中:B2为带宽,GjPU为PBS-UAV到第j(j=1, 2, …, J)个用户的信道增益,N1为噪声功率.
需要注意,在T1时间段内,由FBS向用户发送信号,噪声功率为N0.在T2时间段内,由PBS-UAV向用户发送信号,噪声功率为N1.由于T1和T2时间段内,基站所处的位置和用户数量都发生了改变,所以噪声功率不相等.
功率分配策略的目标是最大化T1和T2总时间段内的下行信息量,同时受到一些约束条件的限制.该问题是一个最优化问题,可以建模为
| $ {{\rm{ }}\mathop {{\rm{maximize}}}\limits_{P_i^{{\rm{FT}}},P_j^{{\rm{PT}}}} {\rm{ }}H = \mu N{T_1}{R_{\rm{F}}} + \xi {T_2}{R_{\rm{P}}}} $ | (7a) |
| $ {{\rm{ s}}{\rm{. t}}{\rm{. }}{E_{\rm{F}}} \le \tau {E_{{\rm{F1}}}}} $ | (7b) |
| $ {{E_{\rm{P}}} \le {E_{{\rm{P1}}}} + (1 - \tau )N\theta {E_{{\rm{F1}}}}} $ | (7c) |
| $ {0 < P_i^{{\rm{FT}}} \le P_{{\rm{max}}}^{\rm{F}}} $ | (7d) |
| $ {0 < P_j^{{\rm{PT}}} \le P_{{\rm{max}}}^{\rm{P}}} $ | (7e) |
其中:τ表示在T1时间段内FBS消耗能量的比例,θ为FBS的剩余能量转移给PBS-UAV的能量转化效率.约束条件式(7b)和式(7c)保证FBS和PBS-UAV消耗的总能量不超过剩余总能量上限,约束条件式(7d)和式(7e)表示FBS和PBS-UAV的发射功率不超过最高功率上限PmaxF和PmaxP,且大于0.
对于上述问题,可以转化为求最小值问题,即
| $ {{\rm{ }}\mathop {{\rm{minimize}}}\limits_{P_i^{{\rm{FT}}},P_j^{{\rm{PT}}}} {\rm{ }}H = - \mu N{T_1}{R_{\rm{F}}} + \xi {T_2}{R_{\rm{P}}}} $ | (8a) |
| $ {{\rm{ s}}{\rm{. t}}{\rm{. }}{E_{\rm{F}}} \le \tau {E_{{\rm{F1}}}}} $ | (8b) |
| $ {{E_{\rm{P}}} \le {E_{{\rm{P1}}}} + (1 - \tau )N\theta {E_{{\rm{F1}}}}} $ | (8c) |
| $ {0 < P_i^{{\rm{FT}}} \le P_{{\rm{max}}}^{\rm{F}}} $ | (8d) |
| $ {0 < P_j^{{\rm{PT}}} \le P_{{\rm{max}}}^{\rm{P}}} $ | (8e) |
式(8)的目标函数由2个对数函数及常量的乘积做加法,这2个对数函数为凸函数.由于若干个凸函数相加或相减仍然是凸函数,同时凸函数与常数相乘不改变凸性质,所以式(8)的目标函数是凸函数.此外,式(8)的约束条件也是关于自变量的凸函数.因此,式(8)为凸优化[15]问题.可以采用增广拉格朗日乘子法求解.为了表示方便,令
| $ {A = {P_{{\rm{FR}}}}(1 - \mu ){T_1} + {P_{{\rm{CF}}}}{T_1}} $ | (9a) |
| $ {B = {P_{{\rm{PR}}}}(1 - \xi ){T_2} + {P_{{\rm{CP}}}}{T_2}} $ | (9b) |
将式(9a)和式(9b)代入式(8a)和式(8b),并进行化简,可以得到
| $ \begin{array}{l} \mathop {{\rm{ minimize}}}\limits_{P_t^{{\rm{FT}}},P_j^{{\rm{PT}}}} - \mu N{T_1}{B_1}\sum\limits_{i = 1}^I { {\rm{lb}} } \left( {1 + \frac{{P_i^{{\rm{FT}}}|G_i^{{\rm{FU}}}{|^2}}}{{{N_0}}}} \right) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \xi {T_2}{B_2}\sum\limits_{j = 1}^J {{\rm{ lb }}} \left( {1 + \frac{{P_j^{{\rm{PT}}}|G_j^{{\rm{PU}}}{|^2}}}{{{N_1}}}} \right) \end{array} $ | (10a) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tau {E_{{\rm{F1}}}} - \sum\limits_{i = 1}^I {P_i^{{\rm{FT}}}} \mu {T_1} - A \ge 0 $ | (10b) |
| $ {E_{{\rm{P1}}}} + (1 - \tau )N\theta {E_{{\rm{F1}}}} - B - \sum\limits_{j = 1}^J {P_j^{{\rm{PT}}}} \xi {T_2} \ge 0 $ | (10c) |
| $ {P_{{\rm{max}}}^{\rm{F}} - P_i^{{\rm{FT}}} \ge 0} $ | (10d) |
| $ {P_{{\rm{max}}}^{\rm{P}} - P_i^{{\rm{PT}}} \ge 0} $ | (10e) |
此外,
| $ \begin{array}{l} {f_0}({\mathit{\boldsymbol{P}}_{{\rm{FT}}}},{\mathit{\boldsymbol{P}}_{{\rm{PT}}}}) = - \mu N{T_1}{B_1}\sum\limits_{i = 1}^I {{\rm{ lb }}} \left( {1 + \frac{{P_i^{{\rm{FT}}}|G_i^{{\rm{FU}}}{|^2}}}{{{N_0}}}} \right) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \xi {T_2}{B_2}\sum\limits_{j = 1}^J {{\rm{ lb }}} \left( {1 + \frac{{P_j^{{\rm{PT}}}|G_j^{{\rm{PU}}}{|^2}}}{{{N_1}}}} \right) \end{array} $ | (11a) |
| $ {f_1}({\mathit{\boldsymbol{P}}_{{\rm{FT}}}}) = \tau {E_{{\rm{F1}}}} - \sum\limits_{i = 1}^I {P_i^{{\rm{FT}}}} \mu {T_1} - A $ | (11b) |
| $ {f_2}({\mathit{\boldsymbol{P}}_{{\rm{PT}}}}) = {E_{{\rm{P1}}}} + (1 - \tau )N\theta {E_{{\rm{F1}}}} - B - \sum\limits_{i = 1}^J {P_j^{{\rm{PT}}}} \xi {T_2} $ | (11c) |
| $ {{f_{3,i}}(P_i^{{\rm{FT}}}) = P_{{\rm{max}}}^{\rm{F}} - P_i^{{\rm{FT}}}} $ | (11d) |
| $ {{f_{4,j}}(P_j^{{\rm{PT}}}) = P_{{\rm{max}}}^{\rm{P}} - P_j^{{\rm{PT}}}} $ | (11e) |
式(11d)中,i=1, 2, …, I.式(11e)中,j=1, 2, …, J.可以把问题(10)转化为
| $ {\mathop {{\rm{minimize}}}\limits_{{\mathit{\boldsymbol{P}}_{{\rm{FT}}}},{\mathit{\boldsymbol{P}}_{{\rm{PT}}}}} {f_0}({\mathit{\boldsymbol{P}}_{{\rm{FT}}}},{\mathit{\boldsymbol{P}}_{{\rm{PT}}}})} $ | (12a) |
| $ {{\rm{ s}}{\rm{.t}}{\rm{. }}{f_1}({\mathit{\boldsymbol{P}}_{{\rm{FT}}}}) \ge 0} $ | (12b) |
| $ {{f_2}({\mathit{\boldsymbol{P}}_{{\rm{PT}}}}) \ge 0} $ | (12c) |
| $ {{f_{3,i}}(P_i^{{\rm{FT}}}) \ge 0} $ | (12d) |
| $ {{f_{4,j}}(P_j^{{\rm{PT}}}) \ge 0} $ | (12e) |
对于上述凸优化问题,可以得到关于式(12)的增广拉格朗日函数为[16]
| $ \begin{array}{l} \frac{1}{{2\lambda }}\sum\limits_{i = 1}^I {(\{ } {\rm{max}}[0,{\omega _1} - \lambda {f_1}({\mathit{\boldsymbol{P}}_{{\rm{FT}}}})]{\} ^2} - \omega _1^2) + \\ \frac{1}{{2\lambda }}\sum\limits_{j = 1}^J {(\{ } {\rm{max}}[0,{\omega _2} - \lambda {f_2}({\mathit{\boldsymbol{P}}_{{\rm{PT}}}})]{\} ^2} - \omega _2^2) + \\ \frac{1}{{2\lambda }}\sum\limits_{i = 1}^I {(\{ } {\rm{max}}[0,{\omega _{3,i}} - \lambda {f_{3,i}}(P_i^{{\rm{FT}}})]{\} ^2} - \omega _{3,i}^2) + \\ \frac{1}{{2\lambda }}\sum\limits_{j = 1}^J {(\{ } {\rm{max}}[0,{\omega _{4,j}} - \lambda {f_{4,j}}(P_j^{{\rm{PT}}})]{\} ^2} - \omega _{4,j}^2) \end{array} $ | (13) |
其中:ω=[ω1, ω2, ω3, 1, ω3, 2, …, ω3, I, ω4, 1, ω4, 2, …, ω4, J]为一个向量,λ为惩罚因子,ω1,ω2,ω3, i和ω4, j对应于f1(PFT),f2(PPT),f3, i(PiFT)和f4, j(PjPT)的乘子.通过增广拉格朗日乘子法将式(12)中的不等式约束的凸优化问题转化成求解无约束问题:
| $ \mathop {{\rm{minimize}}}\limits_{{\mathit{\boldsymbol{P}}_{{\rm{FT}}}},{\mathit{\boldsymbol{P}}_{{\rm{PT}}}}} ({\mathit{\boldsymbol{P}}_{{\rm{FT}}}},{\mathit{\boldsymbol{P}}_{{\rm{PT}}}},\mathit{\boldsymbol{\omega }},\lambda ) $ | (14) |
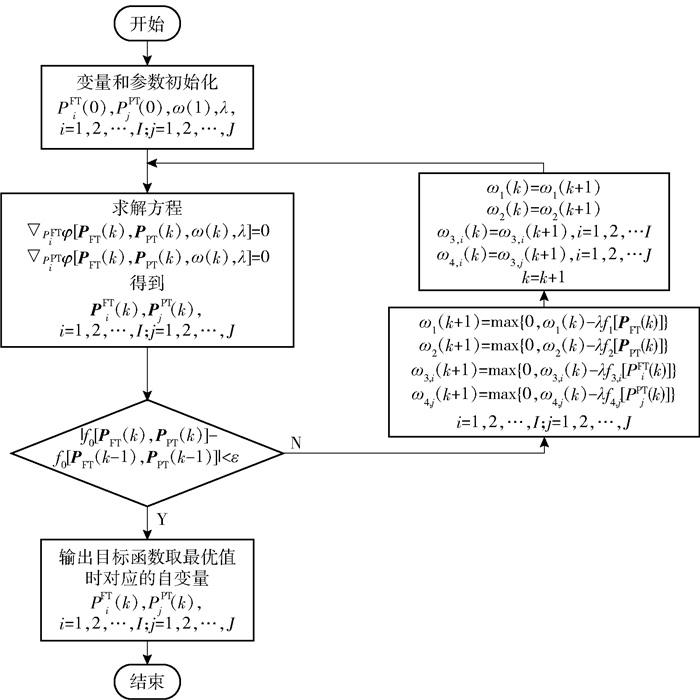
求解问题(14)的算法流程如图 2所示.在图 2中,PFT(k)、PPT(k)和ω(k)为第k次迭代运算时对应的取值,ε为算法迭代停止时目标函数下降精度.
|
图 2 增广拉格朗日乘子法流程 |
通过图 2所示的算法流程,最终可以得到问题(14)的最优解,从而确定FBS和PBS-UAV到用户的发射功率,使得FBS和PBS-UAV在T1和T2总时间内到用户的下行信息量达到最大.
3 性能评估通过仿真对前文所提出的功率分配策略进行性能评估.在仿真中,假设忙时T1阶段每个FBS服务I=2个用户,闲时T2阶段有J=5个用户,即PBS-UAV同时对5个用户进行服务.在仿真中,使用服从均匀分布的随机数产生下行信道增益.其他相关参数设置为T1=100s,T2=100s,N=5,PM1=43dBm[17],GMF=0.7,γ=0.7,ζ=0.7,GMP=0.8,EU0=380J,PUF=5W,PUH=1W,μ=0.87,ξ=0.92,PFR=PPR=5×10-7W,PCF=PCP=5×10-7W,B1=B2=15kHz,N0=-40dBm,N1=-30dBm,PmaxF=2W,PmaxP=5W,τ=0.5和θ=0.67.
在仿真中,对提出方法和其他方法性能进行对比.其他方法包括:有PBS-UAV的等功率方法(EP-PU,equal power method with PBS-UAV);有PBS-UAV的忙时固定功率方法(BFP-PU,busy time fixed power method with PBS-UAV);有PBS-UAV的闲时固定功率方法(SFP-PU,spare time fixed power method with PBS-UAV). EP-PU是指在PBS-UAV参与的情况下,FBS和PBS-UAV分别在忙时T1和闲时T2阶段将可用的发射功率进行平均分配;BFP-PU指的是在PBS-UAV参与的情况下,在繁忙时间段T1,FBS采用固定功率方式发送数据,固定功率值设定为0.8448W,它取自提出方法在η=0.3时FBS的发射功率.在闲时T2阶段,使用增广拉格朗日乘子法进行求解;SFP-PU指的是在PBS-UAV参与的情况下,在空闲时间段T2,PBS-UAV采用固定功率方式发送数据,固定功率值设定为1.8779W,它取自提出方法在η=0.3时PBS-UAV的发射功率.在忙时T1阶段,使用增广拉格朗日乘子法进行求解.
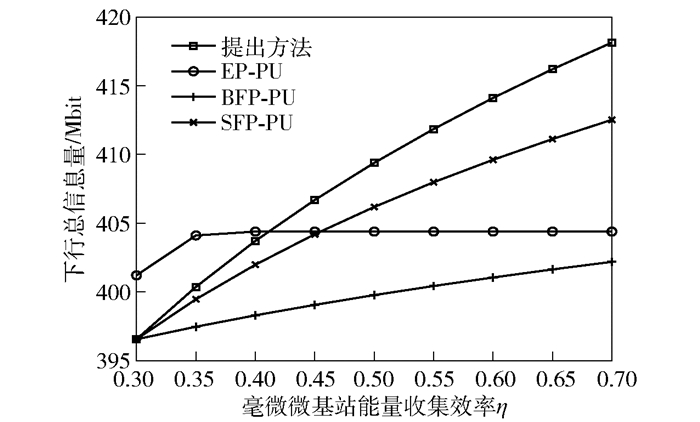
图 3所示为不同方法时下行总信息量和FBS能量收集效率η之间的关系.从图中可以看出,随着η的提高,5种方法得到的下行总信息量都有所提高.其中,从η=0.42时开始,提出方法优于EP-PU方法,这是因为受到FBS发射功率上限的影响,在忙时T1阶段存在一部分未被使用的剩余能量,笔者提出的方法可以将这部分剩余能量更有效地利用起来,从而提高下行总信息量.此外,笔者提出的方法始终优于BFP-PU和SFP-PU.这是因为,相较于部分功率固定的方式,笔者提出的方法能够充分使用可用功率,从而使总的下行信息量得以提升.同时,SFP-PU优于BFP-PU.这是因为,虽然两种方法都采用了固定功率的方式,但固定功率的时间段却不同,从2种方法在图中对应的曲线可以看出,忙时T1固定FBS的发射功率比闲时T2固定PBS-UAV的发射功率对总的下行信息量影响更为显著.
|
图 3 不同方法时下行总信息量和η的关系 |
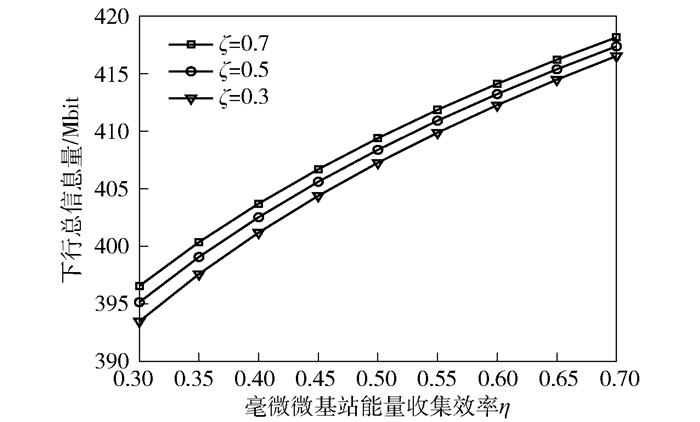
图 4所示为所提出的方法在不同PBS-UAV能量收集效率ζ的情况下,T1和T2阶段下行总信息量和FBS能量收集效率η之间的关系.可以看出,对于相同的η,当ζ的取值越大,下行总信息量越大.原因在于,在FBS能量收集效率一定的情况下,ζ取值越大,提供给PBS-UAV在T2阶段所能使用的功率越大,下行总信息量相应增加.
|
图 4 不同ζ时下行总信息量和η的关系 |
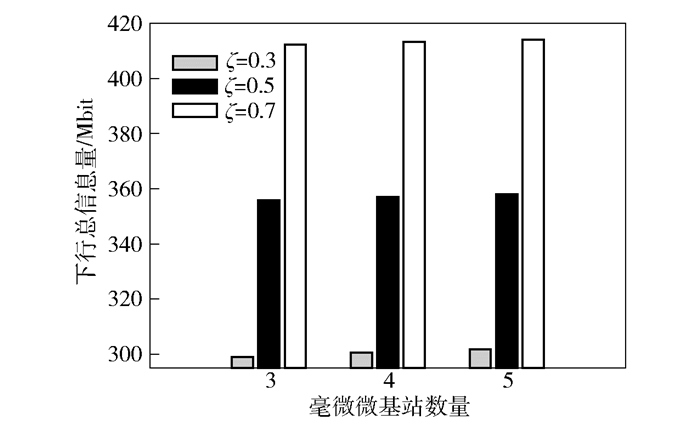
图 5所示为所提出的方法在不同PBS-UAV能量收集效率ζ的情况下,T1和T2阶段下行总信息量和FBS数量之间的关系.从图中可以看出,在ζ一定的情况下,随着FBS的数量从3个增加到5个,T1和T2阶段下行总信息量略微提升.原因分析如下:从仿真参数设置来看,在忙时T1时间段,3个FBSs共有6个用户(每个FBS有2个用户),5个FBSs共有10个用户.在闲时T2时间段,无论是3个FBSs,还是5个FBSs,总用户数量都是5个.因此,3个FBSs和5个FBSs情况下整个忙时和闲时的用户数量差异不大,导致总信息量略微增加.如果FBSs数量更多,总信息量差异会更明显.此外,在FBS数量一定的情况下,改变ζ,对T1和T2阶段下行总信息量有显著影响.这是因为,当FBS数量一定时,ζ增大,会增加PBS-UAV收集到的能量,使下行总信息量增大.
|
图 5 不同ζ时下行总信息量和FBS数量的关系 |
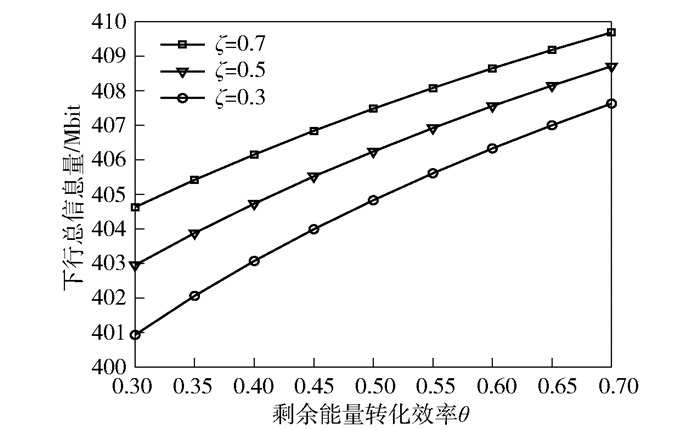
图 6所示为所提出的方法在不同的PBS-UAV能量收集效率ζ的情况下,下行总信息量和FBS剩余能量转移给PBS-UAV的能量转化效率θ之间的关系.当ζ取值一定时,随着θ取值增大,PBS-UAV可用的能量增加,PBS-UAV的功率随之增大,下行总信息量增大.然而,在θ取值增大的同时,不同ζ取值之间的下行总信息量之间的差值在逐渐缩小.这是因为当θ取值和ζ取值同时增大时,θ相较于ζ会对总的下行信息量产生更大的影响.
|
图 6 不同ζ时下行总信息量和θ的关系 |
针对FBS在忙时和闲时存在用户数量的差异,提出了一种UAV协助的分时段最大化下行总信息量的功率分配策略.通过部署一个具有能量收集功能的PBS-UAV,与多个FBSs闲时的用户进行通信.当FBS忙时,FBS和PBS-UAV同时从MBS收集能量,并且FBS向用户发送数据.当FBS闲时,PBS-UAV接替FBS的工作,与用户进行下行通信.在保证PBS-UAV和FBS的能量消耗和发射功率的前提下,以最大化下行总信息量为目标,通过增广拉格朗日乘子法获得最优解.仿真结果显示,与PBS-UAV参与的等功率及部分功率固定的方法相比,提出的方法在下行总信息量方面有不同程度的增加.由于假设每个FBS具有相同的用户数量,并且数量较少,未来将考虑更多的用户以及不同的FBSs用户数量的差异,充分调动PBS-UAV可移动性的优势,从提高能量效率的角度来进行进一步研究.
| [1] |
Lu Xiao, Wang Ping, Niyato D, et al. Wireless networks with RF energy harvesting:a contemporary survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 757-789. |
| [2] |
Ku M L, Li Wei, Chen Yan, et al. Advances in energy harvesting communications:past, present, and future hallenges[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 1384-1412. |
| [3] |
Zhao Yisheng, Leung V C M, Sun Xinghua, et al. Energy-efficient resource allocation in cellular network with ambient RF energy harvesting[C]//2017 Wireless Communications & Networking Conference(WCNC). San Francisco: IEEE Press, 2017: 1-6.
|
| [4] |
Guo Songtao, Shi Yawei, Yang Yuanyuan, et al. Energy efficiency maximization in mobile wireless energy harvesting sensor networks[J]. IEEE Transactions on Mobile Computing, 2018, 17(7): 1524-1537. DOI:10.1109/TMC.2017.2773067 |
| [5] |
Luo Ying, Hong Peilin, Su Ruolin, et al. Resource allocation for energy harvesting-powered D2D communication underlaying cellular networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 10486-10498. DOI:10.1109/TVT.2017.2727144 |
| [6] |
Lohani S, Hossain E, Bhargava V K. Joint resource allocation and dynamic activation of energy harvesting small cells in OFDMA HetNets[J]. IEEE Transactions on Wireless Communications, 2018, 17(3): 1768-1783. DOI:10.1109/TWC.2017.2785301 |
| [7] |
Wang Haichao, Wang Jinlong, Ding Guoru, et al. Resource allocation for energy harvesting-powered D2D communication underlaying UAV-assisted networks[J]. IEEE Transactions on Green Communications and Networking, 2018, 2(1): 14-24. DOI:10.1109/TGCN.2017.2767203 |
| [8] |
Yang Liang, Chen Jianchao, Hasna M O, et al. Outage performance of UAV-assisted relaying systems with RF energy harvesting[J]. IEEE Communications Letters, 2018, 22(12): 2471-2474. DOI:10.1109/LCOMM.2018.2876869 |
| [9] |
Xie Lifeng, Xu Jie, Zhang Rui. Throughput maximization for UAV-enabled wireless powered communication networks[J]. IEEE Internet of Things Journal, 2019, 6(2): 1690-1703. |
| [10] |
Pan Yu, Da Xinyu, Hu Hang, et al. Energy-efficiency optimization of UAV-based cognitive radio system[J]. IEEE Access, 2019, 7: 155381-155391. DOI:10.1109/ACCESS.2019.2939616 |
| [11] |
Hua Meng, Wang Yi, Li Chunguo, et al. UAV-aided mobile edge computing systems with one by one access scheme[J]. IEEE Transactions on Green Communications and Networking, 2019, 3(3): 664-678. DOI:10.1109/TGCN.2019.2910590 |
| [12] |
Zhu Zhengyu, Chu Zheng, Wang Zhongyong, et al. Outage constrained robust beamforming for secure broadcasting systems with energy harvesting[J]. IEEE Transactions on Wireless Communications, 2016, 15(11): 7610-7620. DOI:10.1109/TWC.2016.2605102 |
| [13] |
Chu Zheng, Zhu Zhengyu, Johnston M, et al. Simultaneous wireless information power transfer for MISO secrecy channel[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 6913-6925. DOI:10.1109/TVT.2015.2499439 |
| [14] |
Chu Zheng, Zhou Fuhui, Xiao Pei, et al. Resource allocation for secure wireless powered integrated multicast and unicast services with full duplex self-energy recycling[J]. IEEE Transactions on Wireless Communications, 2019, 18(1): 620-636. |
| [15] |
Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004.
|
| [16] |
陈宝林. 最优化理论与算法[M]. 第2版. 北京: 清华大学出版社, 1989: 405-413.
|
| [17] |
Zhao Yisheng, Leung V C M, Zhu Chunsheng, et al. Energy-efficient sub-carrier and power allocation in cloud-based cellular network with ambient RF energy harvesting[J]. IEEE Access, 2017, 5: 1340-1352. DOI:10.1109/ACCESS.2017.2667678 |



