2. 哈尔滨工业大学 电子与信息工程学院, 哈尔滨 150080
认知无线电可通过频谱感知提高资源利用率,但会产生感知能耗,降低传输能量.为了保证认知无线电的传输性能,提出认知无线电可利用多载波实现无线携能通信,并分配通信资源,实现系统性能优化.认知无线电利用部分子载波传输信息,采集剩余子载波上主用户射频能量,补充感知耗能.提出的子载波和子载波功率联合优化算法,在保证能量、干扰和总功率受约束的基础上,可最优化系统的吞吐量和能量.仿真结果表明,能量采集会占用传输资源,需要合理分配子载波,使其在速率和能量间取得性能折中.提出的算法通过采集能量补充感知能耗有效地提高了系统吞吐量.
2. School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150080, China
Cognitive radio can improve spectrum utilization through sensing spectrum, but it may generate circuit energy consumption, which decreases transmission energy.In order to guarantee transmission performance, a multi-carrier is proposed to realize simultaneous wireless information and power transfer whose optimal performance can be achieved through communication resource allocations.Cognitive radio uses some subcarriers to transmit information and collect the primary user radio frequency energy on the remaining subcarriers to supplement the perceived energy consumption.A joint optimization algorithm of subcarrier set and subcarrier power is proposed, which can maximize system performance subject the constraints of energy, interference and total power.Simulations show that energy harvesting may occupy transmission resources, a reasonable allocation of subcarriers is required to achieve a tradefoff between rate and energy.The proposed algorithm effectively improves system throughput by collecting energy to supplement sensing energy consumption.
随着通信用户的急剧增长和高质量通信业务的要求,无线频谱已经成为一种宝贵的资源.传统的静态频谱分配将某一频谱分配给特定用户使用,因此,频谱利用率较低且难以满足未来的通信需求[1-3].认知无线电系统基于频谱共享机理,允许认知用户和主用户利用同一频谱通信.但是,认知用户必须控制自身发射功率,避免对主用户产生任何干扰[4-5].
无线携能通信是当前热点技术,无线通信系统在接收信号的同时采集部分信号的能量为自身提供电能[6-8].常用的无线携能通信方法包括:功率分流和时隙转换.功率分流能够将接收信号分割成两个数据流,分别用于信息传输和能量采集;时隙转换允许接收机在不同时隙进行信息传输和能量采集.但是功率分流方案会导致信息损失,而时隙转换方案会引起传输延迟[9-10].杜研究了多载波无线携能通信的资源优化算法[11],通过优化子载波功率和分配系数,在保证采集能量的同时最大化系统吞吐量. Huang等将能量采集用于认知无线电中,认知用户可以采集主用户的能量补充电能[12],但是能量采集和信息传输是在不同时隙独立完成的. Lee等提出了频谱感知协同能量采集[13],认知用户接收机感知授权用户的同时采集授权用户能量,但是需要单独的感知时隙,导致频谱利用率降低.综上,传统方法具有信息损失、传输延迟和频谱利用率低等缺点[14].
笔者提出一种能够无线携能通信的多载波认知无线电系统,利用部分子载波与主用户共享频谱进行信息传输,同时利用剩余子载波采集主用户能量.通过联合优化子载波集合和子载波功率,最大化系统的吞吐量和采集能量.
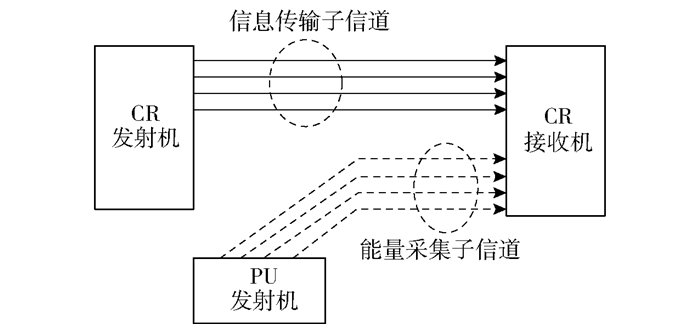
1 系统模型提出一种基于频谱共享的多载波认知无线电(CR,cognitive radio)系统,CR用户能够与主用户(PU,primary user)同时传输信息,但是必须控制各子载波总的发射功率避免对PU产生任何干扰. CR具有无线携能通信的功能,如图 1所示,CR接收机利用一部分子载波传输信息,同时利用剩余子载波采集PU的射频能量补充电能.
|
图 1 CR无线携能通信资源分配模型 |
假设总共有M个子载波,其中N个子载波传输信息,M-N个子载波用于采集能量.定义总的子载波集合为W,信息子载波集合和能量子载波集合分别为Ωi和Ωe,因此Ωi∪Ωe=W.假设CR在子载波i上的传输功率为pi、信道增益为hi,噪声功率为σi. CR的频谱效率(归一化吞吐量)可表示为
| $ R = \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{\rm{log}}} \left( {1 + \frac{{{p_i}h_i^2}}{{p_i^sg_i^2 + {\sigma _i}}}} \right) $ | (1) |
其中:pis为PU的子载波发射功率,gi为PU发射机和CR接收机之间的信道增益. CR采集的能量可表示为
| $ {E_{\rm{h}}} = \mu \sum\limits_{i \in {\varOmega _{\rm{e}}}} {(p_i^sg_i^2 + {\sigma _i})} t $ | (2) |
其中:μ为能量采集效率,t为系统工作时间.接收机采集的能量需要满足系统电路损耗,即
| $ {E_{\rm{h}}} + {E_0} \ge {p_{\rm{c}}}t $ | (3) |
其中pc为电路损耗功率,E0为电路自身能量供应.
为了避免对PU产生任何干扰,CR对PU产生的干扰功率应该受到控制,即
| $ \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} f_i^2 \le {P_{\rm{I}}} $ | (4) |
其中:fi为CR发射机和PU接收机之间的信道增益,PI为最大干扰功率.同时,CR的发射总功率需要受到控制,即
| $ \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} \le {P_{\rm{t}}} $ | (5) |
其中Pt是最大功率.
2 模型优化 2.1 最大化吞吐量最大化吞吐量模型的优化目标是:在保证采集能量满足系统需求、干扰和总功率受约束基础上,通过优化子载波集合和子载波功率最大化系统吞吐量.优化模型表示为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\mathop {{\rm{max}}}\limits_{{\varOmega _{\rm{i}}},{\varOmega _{\rm{e}}},\left\{ {{p_i}} \right\}} R}\\ {{\rm{约束条件 }}\quad {E_{\rm{h}}} + {E_0} \ge {p_{\rm{c}}}t} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} f_i^2 \le {P_{\rm{I}}}}\\ {\sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} \le {P_{\rm{t}}}}\\ {{p_i} \ge 0,i \in {\varOmega _{\rm{i}}}}\\ {{\varOmega _{\rm{i}}} \cup {\varOmega _{\rm{e}}} = N} \end{array} \end{array} $ | (6) |
首先由Eh+E0≥pct得到
| $ \sum\limits_{i \in {\varOmega _{\rm{e}}}} {{\varPhi _i}} \ge \frac{{{p_{\rm{c}}} - {p_0}}}{u} $ | (7) |
其中:p0为电源供给功率,u为时间t与能量采集效率μ的比值,Φi=pisgi2+σi.
若pc≤p0,则表明电源供给满足电路消耗,因此不需能量采集,即Ωe=0.若pc>p0,需要选择若干子载波采集能量.由式(1)和式(2)可知,Φi越大,吞吐量越小,而采集的能量越多,因此优先选择Φi较大的子载波用于能量采集,此时可以减少能量采集的子载波数,从而将更多的子载波用于信息传输,进而提高吞吐量.
将子载波按照Φi的值从大到小排列,选取前面的子载波采集能量,直至满足式(7),将这些子载波归类Ωe,剩余子载波归类Ωi用于信息传输.因此,优化问题(6)简化为
| $ \begin{array}{*{20}{l}} {\mathop {{\rm{max}}}\limits_{\{ {p_i}\} } R = \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{\rm{log}}} \left( {1 + \frac{{{p_i}h_i^2}}{{{\varPhi _i}}}} \right)}\\ {{\rm{约束条件 }}:\sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} f_i^2 \le {P_{\rm{I}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} \le {P_{\rm{t}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {p_i} \ge 0,i \in {\varOmega _{\rm{i}}}} \end{array} $ | (8) |
上述问题属于凸优化问题,可以采用拉格朗日算法求解.拉格朗日函数表示为
| $ \begin{array}{*{20}{c}} {G(\{ {p_i}\} ) = \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{\rm{log}}} \left( {1 + \frac{{{p_i}h_i^2}}{{{\varPhi _i}}}} \right) + }\\ {{\lambda _1}\left( {{P_{\rm{I}}} - \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} f_i^2} \right) + {\lambda _2}({P_{\rm{t}}} - \sum\limits_{i \in {\varOmega _{\rm{i}}}} {{p_i}} )} \end{array} $ | (9) |
其中拉格朗日乘子λ1>0和λ2>0.最优值{pi*}可以由
| $ p_i^* = {\left( {\frac{1}{{{\lambda _1}f_i^2 + {\lambda _2}}} - \frac{{{\varPhi _i}}}{{h_i^2}}} \right)^ + } $ | (10) |
其中(x)+表示x和0中的最大值.此时,λ1和λ2可以由如下迭代算法计算:
| $ \left. {\begin{array}{*{20}{l}} {\lambda _1^{(t + 1)} = \lambda _1^{(t)} + \mu _1^{(t)}({P_{\rm{I}}} - \sum\limits_{i \in {\varOmega _{\rm{i}}}} {p_i^*} f_i^2)}\\ {\lambda _2^{(t + 1)} = \lambda _2^{(t)} + \mu _2^{(t)}({P_{\rm{t}}} - \sum\limits_{i \in {\varOmega _{\rm{i}}}} {p_i^*} )} \end{array}} \right\} $ | (11) |
其中t为迭代次数,0 < μ1(t), μ2(t) < 1为迭代步长.
算法1表述如下.
1) 将子载波按照Φi从大到小排列,子载波序号记作1, 2, …, N;
2) 选择前l个子载波刚好满足式(7),集合记为Ωe,剩余子载波归类Ωi;
3) 初始化λ1和λ2,μ1和μ2,可取λ1=2,λ2=3,μ1=0.1,μ2=0.3;
4) 根据式(10)计算pi*;
5) 代入式(11)更新λ1和λ2;
重复步骤4)和5)直到λ1和λ2全部收敛;
将收敛的λ1和λ2代入式(10)求子载波功率.
2.2 最大化能量最大化能量的优化目标是:在保证吞吐量满足要求、干扰和总功率受约束的基础上,最大化认知无线电采集的能量.优化问题表示为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\mathop {{\rm{max}}}\limits_{{\varOmega _{\rm{i}}},{\varOmega _e},\{ {p_i}\} } {E_{\rm{h}}}}\\ {{\rm{约束条件}}:{\rm{R}} \ge {{\rm{R}}_{{\rm{min}}}}} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\sum\limits_{i \in {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{i}}}} {{p_i}} f_i^2 \le {P_{\rm{I}}}}\\ {\sum\limits_{i \in {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{i}}}} {{p_i}} \le {P_{\rm{t}}}}\\ {{p_i} \ge 0,i \in {\varOmega _{\rm{i}}}}\\ {{\varOmega _{\rm{i}}} \cup {\varOmega _{\rm{e}}} = N} \end{array} \end{array} $ | (12) |
上述问题目标函数为线性函数,因此很难用凸优化问题求解.下面给出一种次优求解方法.选择Φi最大的子载波采集能量,选择Φi最小的子载波传输信息,同时传输信息的子载波数量越少,可获得的采集能量越大.因此,可以采用枚举法,依次选择前面的若干子载波,并通过式(8)进行优化,计算最大频谱效率R,当刚好满足R≥Rmin时,将选择的子载波归类为Ωi,其余归类为Ωe.
算法2的流程表述如下.
1) 将子载波按照Φi从小到大排列,子载波序号记作1, 2, …, N;
2) 依次选取前l=1, 2, …个子载波,利用式(8)求得R的最大值;
3) 当刚好满足R≥Rmin时,将l个子载波归类为Ωi;其余子载波归类为Ωe.
3 仿真分析仿真中子载波数为36,噪声功率为0.1mW,能量采集效率为0.5,系统自身储能为5mJ,信道服从均值为-10dB的瑞利分布.
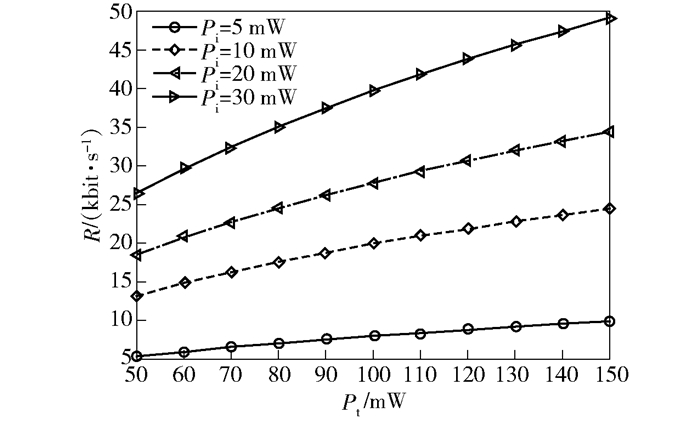
最大化吞吐量情况下的模型性能仿真如图 2所示,表示干扰功率Pi={5, 10, 20, 30}mW时,认知无线电频谱效率R随总功率Pt的变化.可以看出,认知无线电的传输速率随着总功率的增加急剧增长,表明总功率越大,提出算法的资源分配效益越明显.传输速率随着干扰功率限制的降低而下降,表明为了控制对主用户的干扰,认知无线电不得不选择较差的信道传输信息.
|
图 2 不同干扰功率下认知无线电的传输速率随总功率的变化 |
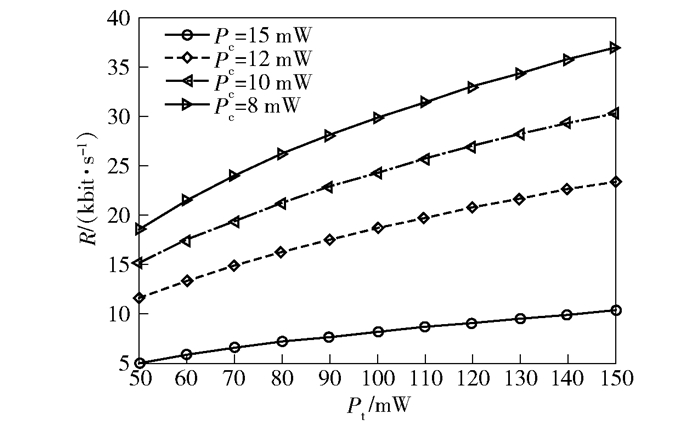
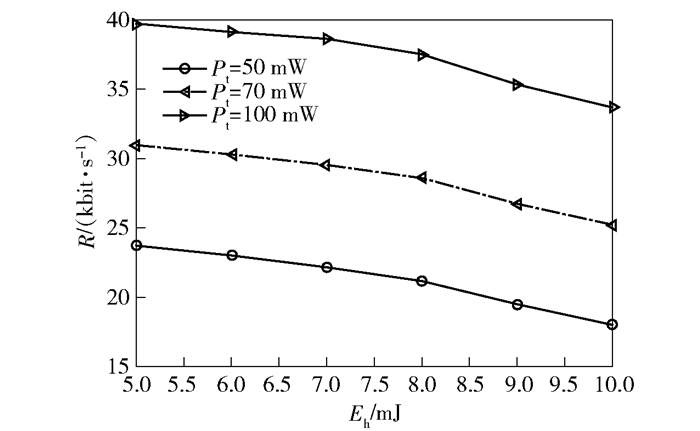
图 3表示电路损耗功率pc={15, 12, 10, 8}时认知无线电的信息传输速率随总功率的变化,可以看出,损耗功率越大,认知无线电的信息传输速率越低.这是因为损耗功率增加,认知无线电需要更多、更好的子载波传输信息,因而用于传输信息的子载波的数量和质量会较低,认知无线电的频谱效率下降.图 4给出了总功率Pt={50, 70, 100}时,信息传输速率随采集能量Eh的变化,可以看出,传输速率随着采集能量的增加而减少,这表明能量采集会占用传输资源,需要选择合适数量的子载波采集能量,从而在信息传输和能量采集之间取得折中.
|
图 3 不同电路损耗功率下认知无线电的传输速率随总功率的变化 |
|
图 4 不同总功率下认知无线电的传输速率随采集能量的变化 |
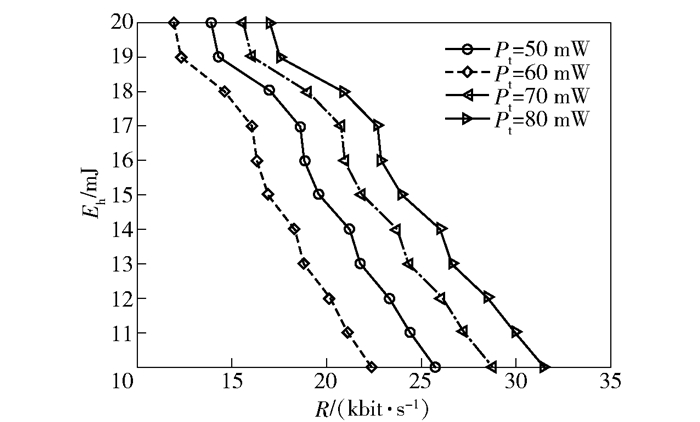
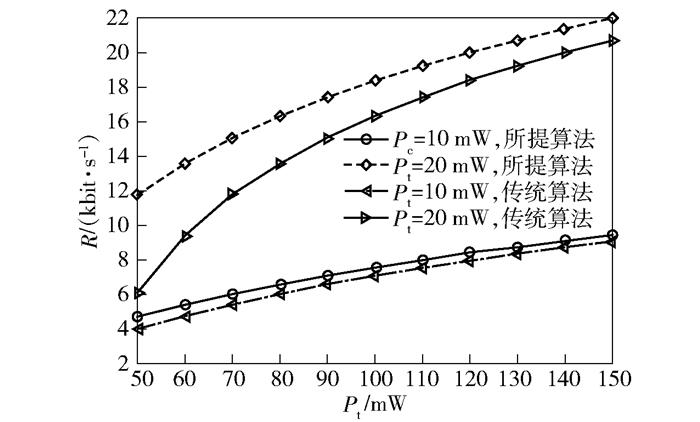
图 5给出了最大化采集能量的情况下,当Pt={50, 60, 70, 80}时,不同频谱效率限值下的最大采集能量.可以看出,频谱效率要求增加时,采集能量减小,表明系统耗能显著增加.此外,当总功率增加时,采集能量增加,表明信号携带的能量有所提高.图 6所示为提出的算法与传统注水算法吞吐量相比较的结果,可以看出,提出算法的频谱效率有一定提高,因为提出算法通过采集能量补充了感知消耗,传输能量有所提高.
|
图 5 不同频谱效率限值下的最大化采集能量 |
|
图 6 所提算法和传统注水算法的性能比较 |
此外,还对子载波数为10、24、30时的情况进行了仿真,得出的仿真结论与子载波数为36时基本一致,从而证明了结论的普遍性.由于篇幅有限,对仿真结果不再一一列举.
4 结束语提出一种多载波认知无线电携能通信系统,利用部分子载波传输信息,使用剩余子载波采集能量.通过研究联合资源的分配方法,在约束能量、干扰和功率的基础上,有效地提高了系统的性能.相比传统方案,提出的系统通过采集能量补充感知耗能,节约了传输能耗,因此吞吐量有所提高.此外,资源分配能够有效解决能量采集和信息传输间的资源冲突,从而获得折中性能.下一步将研究多用户场景下无线携能通信的资源分配算法.
| [1] |
Wen Zhigang, Liu Xiaoqing, Chen Yancun, et al. Joint transceiver designs for full-duplex MIMO SWIPT systems based on MSE criterion[J]. China Communications, 2016, 13(10): 79-85. DOI:10.1109/CC.2016.7733034 |
| [2] |
Zhuang Ling, Ma Long. Resource allocation algorithm of multicarrier cognitive radio considering spectrum sensing error[J]. Computer Engineering, 2017, 43(2): 171-175, 182. |
| [3] |
Zhong Chen, Gao Feifei, Zheng Wei. Multiple-level power allocation strategy for secondary users in cognitive radio networks[J]. Journal on Advances in Signal Processing, 2014, 32(1): 89-97. |
| [4] |
Zhuang Yonghong, Liu Lu, Shao Kai, et al. Efficient resource allocation algorithm with rate requirement consideration in muticarrier-based cognitive radio networks[J]. Journal of Communications, 2015, 10(1): 16-23. |
| [5] |
Liu Xin, Bi Guoan, Guan Yongliang, et al. Joint optimization algorithm of cooperative spectrum sensing with cooperative over-head and sub-band transmission power for wideband cognitive radio network[J]. Transactions on Emerging Telecommunications Technologies, 2015, 26(4): 586-597. DOI:10.1002/ett.2675 |
| [6] |
韩松, 李鑫滨, 马锴, 等. 改进的认知无线电系统中频谱共享博弈算法[J]. 北京理工大学学报, 2017, 37(7): 758-764. Han Song, Li Xinbin, Ma Kai, et al. Improved spectrum sharing game algorithm in cognitive radio systems[J]. Journal of Beijing Institute of Technology, 2017, 37(7): 758-764. |
| [7] |
Chen Xiaoming, Hsiao-Hwa, Meng Weixiao. Cooperative communications for cognitive radio networks-from theory to applications[J]. IEEE Communications Surveys & Tutorials, 2014, 16(3): 1180-1192. |
| [8] |
Bi S Z, Ho C K, Zhang R. Wireless powered communication:opportunities and challenges[J]. IEEE Communications Magazine, 2015, 53(4): 117-125. DOI:10.1109/MCOM.2015.7081084 |
| [9] |
Zhang R, Chua K C, Liu L. Secrecy wireless information and power transfer with MISO beamforming[J]. IEEE Transactions on Signal Processing, 2014, 62(71): 1850-1863. |
| [10] |
Liu L, Zhang R, Chua K C. Wireless information transfer with opportunistic energy harvesting[J]. IEEE Transactions on Wireless Communications, 2013, 12(1): 288-300. DOI:10.1109/TWC.2012.113012.120500 |
| [11] |
杜冠瑶.无线协作中继网络的资源分配和信息能量同传技术的研究[D].北京: 北京交通大学, 2015.
|
| [12] |
Huang Gaofei, Zhang Qi, Qin Jiayin. Joint time switching and power allocation for multicarrier decode-and-forward relay networks with SWIPT[J]. IEEE Signal Processing Letters, 2015, 22(12): 2284-2288. DOI:10.1109/LSP.2015.2477424 |
| [13] |
Lee S, Zhang Rui, Huang Kaibin. Opportunistic wireless energy harvesting in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(9): 4788-4799. DOI:10.1109/TWC.2013.072613.130323 |
| [14] |
Liu Xin, Li Feng, Na Zhenyu. Optimal resource allocation in simultaneous cooperative spectrum sensing and energy harvesting for multichannel cognitive radio[J]. IEEE Access, 2017, 5(3): 3801-3812. |



