针对离散尘土颗粒与温度、湿度、电场强度交互作用的复杂条件下,难以有效建立电路板电化学迁移的失效物理模型的问题,通过温湿偏置加速实验,模拟不同积尘密度下电路板的电化学迁移失效,分析颗粒分布密度对电路板绝缘失效时间的作用特性.采用正交实验获取不同尘土颗粒密度、温度、湿度、电场条件下电路板绝缘失效的寿命数据.基于数据驱动的方法,探讨电路板在尘土颗粒污染下的电化学迁移失效寿命建模.对比了多项式回归、机器学习中的梯度提升回归树和随机森林3种方法在尘土分布密度的高低区间内的寿命预测效果.讨论了尘土颗粒污染下利用机器学习建立电路板电化学迁移失效寿命模型的有效性.
Facing the complex conditions that the discrete dust particles interact with the temperature, the humidity, and the electric field intensity, it is difficult to effectively establish the life model of electrochemical migration (ECM) of printed circuit board (PCB) based on failure physics. Through the temperature humidity bias tests, the ECM process under different dust density is simulated. The effect of particle distribution density on time to failure (TTF) of PCB is analyzed. The TTF data of PCB under different particle distribution density, temperature, relative humidity and electric field intensity are obtained by an orthogonal experiment. Based on the data driven method, the ECM life modeling of PCB under dust particle pollution is discussed. The life prediction effects of polynomial regression, gradient boosting regression tree and random forest in machine learning for high and low dust distribution density are compared. The effectiveness of machine learning to establish ECM life model of PCB under dust particle contamination is discussed.
电化学迁移现象是1955年在与电话交换机连接器的镀银端子上发现的[1].它是在一定的温湿环境条件下,电路的正极金属发生离子化,并在电场作用下通过绝缘材料表面吸附水膜向相邻负极迁移,在负极的电子还原形成金属沉积物,直至形成金属原子的晶枝,从而导致两极间绝缘性能下降的一种失效现象[1].
环境湿度、温度和电场强度是引发电路板电化学迁移故障的重要因素.此外,沉积在电路板表面的尘土是电化学迁移的另一个重要的物理化学诱因.我国环境污染严重,尘土随空气进入电子产品内部,沉积在电路板和各种元器件上.尘土颗粒物中约70%为无机物,分为可溶于水和不可溶于水2部分[2].其中可溶部分占4%,可通过吸收大气中的水分,增加电器元件表面湿度,改变水膜离子浓度,降低电路之间的绝缘电阻,加速金属材料腐蚀[3].而不可溶颗粒在电路板表面阻碍散热,其介电特性改变了电路板局部的电场分布,且因毛细管作用吸附水膜,延缓了电路板表面水分的脱附[4].
常用的元器件寿命预测建模方法可分为失效物理方法、统计数据回归方法、机器学习建模方法3种.失效物理建模通常基于失效模式的物理化学原理给出方程. Giulio[5]总结出电化学迁移的失效时间与温度、相对湿度、电场强度等单一因素的关系模型. Yang等[6]建立了电化学迁移失效时间t与温度T、湿度H和电压U三个变量关系的模型,有
| $ t = n{\rm{F}}\frac{{{m_0}}}{M}\beta \frac{1}{U}\frac{{(1 - H)[1 + (c - 1)H]}}{{cH}}{\rm{exp}}\left( {\frac{{{E_\sigma }}}{{RT}}} \right) $ | (1) |
其中:n为迁移金属离子的化合价;F为法拉第常数;m0为绝缘失效时析出金属的质量;M为迁移金属的原子量;β为与绝缘表面吸附水分成反比的参数,取决于测试表面电导率和相对湿度之间的关系;c为与蒸发热和冷凝热相关的参数;Eσ为电解质传导的活化能;R为气体常数.可见,当影响参数增加到3个时,电化学迁移的失效物理模型复杂度已很高.而且通过实验数据验证,采用式(1)进行电路板电化学迁移失效的寿命预测,标准均方差(NMSE, normalized mean square error)为0.215,预测误差较大[7].而如果进一步引入离散分布的尘土颗粒,则难以直接推导电路板电化学迁移失效的物理模型.
统计数据回归建模是指利用数据统计原理,确定因变量与某些自变量的关系,建立回归方程,并加以外推,用于预测因变量的变化.其中,多项式回归建模用于多个自变量与因变量存在多项式函数关系的情况[8-9].谢琪[10]建立了电路板电化学迁移失效时间与温度、湿度、电压3个参数的多项式模型,其NMSE为0.153,预测能力优于基于失效物理的模型,见式(1).
机器学习中的支持向量回归(SVR, support vector regression)、随机森林(RF, random forest)、梯度提升回归树(GBRT, gradient boost regression tree)、神经网络等方法在元器件失效寿命预测领域被广泛应用.而且,RF和GBRT作为集成学习的主要方法在小样本数据中具有较好的应用效果. Wu等[11]基于铣削实验数据,利用RF、人工神经网络、支持向量机3种常用机器学习算法对铣削过程刀具磨损进行回归预测,发现RF能产生更准确的预测. Wang等[12]基于历史天气数据,利用梯度提升决策树(GBDT, gradient boost decision tree)预测模型迭代训练,对未来光伏电池输出进行回归预测.在寿命数据有限的情况下,利用机器学习中的SVR、RF、GBRT算法建立温度、湿度、电场强度3个参数的电路板电化学迁移寿命预测模型,其NMSE分别为0.13、0.065、0.084,准确性显著高于基于失效物理建立的模型和统计数据回归的方法,初步验证了机器学习在电路板电化学迁移失效寿命预测中的可行性[7].
笔者针对尘土不可溶颗粒覆盖对电路板电化学迁移失效现象进行了研究,并探索颗粒分布密度与温度、湿度、偏置电压交互作用下的电路板寿命建模方法.通过温湿偏置加速实验对沉积尘土颗粒的标准电路板模拟电化学迁移失效,分析了尘土颗粒分布密度对电路板绝缘失效寿命的作用特性.采用正交实验获取不同尘土颗粒密度、温度、湿度、偏置电压条件下电路板绝缘失效的寿命数据.基于数据驱动的方法,探讨多项式回归方法、机器学习中的RF和GBRT方法在尘土分布密度高、低区间内的寿命预测建模及其效果.
1 实验研究方案 1.1 颗粒的选取实验主要研究了不可溶性颗粒对电路板电化学迁移的影响.在室内自然沉积的尘土颗粒中石英含量较高,尺寸集中在15~20μm之间[2],因此可将尺寸为13~18μm的石英颗粒作为尘土中不可溶物质的代表.以尘土颗粒的分布密度作为表征不可溶颗粒的特征参数,采用温湿偏置的加速实验,研究不可溶颗粒与温度、相对湿度、偏置电压环境交互作用下对电路板表面电化学迁移失效的影响.
1.2 实验样品测试样品采用FR-4梳状印制电路板,设计参照标准IPC-B-25A,如图 1所示.镀银层厚度为0.15μm,平行线路之间的距离为0.32mm,每块电路板上有3个相同的梳状线路.

|
图 1 梳状电路板样品 |
笔者采用四因素四水平正交实验进行不可溶性颗粒对电路板电化学迁移影响的研究. 4个因素为温度、相对湿度、偏置电压和尘土分布密度.其中,尘土分布密度分为两组:一组为25μg/cm2、100μg/cm2、150μg/cm2、350μg/cm2的低密度水平;另一组为350μg/cm2、450μg/cm2、550μg/cm2、650μg/cm2的高密度水平,分别与温度、相对湿度、偏置电压的四水平构成两组正交实验,如表 1所示.在85℃、93%RH、12V偏置电压下进行了尘土分布密度为0~650μg/cm2的实验,以更明确地说明尘土分布密度单一因素的作用特性.
|
|
表 1 正交实验条件设置 |
电路板电化学迁移实验使用温湿实验箱控制温湿度,外置电压源提供电路板导线之间的偏置电压,然后在温湿箱中放入扬撒了不同分布密度的石英颗粒的电路板.参考《电化学迁移电阻测试标准》(IPC-TM-650 2.6.14.1)[13],通过多路绝缘电阻测试系统监测每个梳状电路板线间表面绝缘电阻变化,从而获取对应于电化学迁移失效的绝缘电阻失效时间.
2 颗粒对电路板电化学迁移的作用通过温湿偏置实验中对电路板上每个梳状电路的表面绝缘电阻进行监测,以及实验后电化学迁移晶枝的生长情况检测,可以研究尘土颗粒对电化学迁移的作用特性和机理.
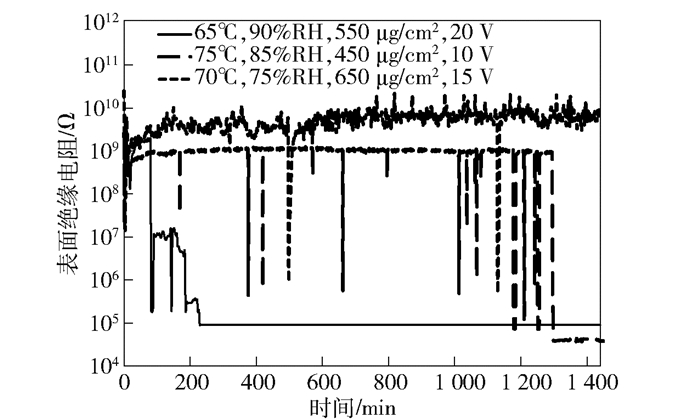
2.1 颗粒与温湿偏置交互下电路板电化学迁移失效分析图 2给出了3种实验条件下的梳状电路板样品24h的表面绝缘电阻曲线.对于65℃、90%RH、550μg/cm2和20V偏置电压条件下的电路板样品,最初表面绝缘电阻在109Ω左右,85min时,表面绝缘电阻突然下降到106Ω,并在106~107Ω波动,232min后,电路板的表面绝缘电阻降低到105Ω,形成稳定的绝缘失效.对于70℃、75%RH、650μg/cm2和15V偏置电压条件下的电路板样品,开始时,表面绝缘电阻在109~1010Ω之间,498min时,表面绝缘电阻突然下降到106Ω,并立即恢复,1130min后,表面绝缘电阻再次下降到106Ω,并立即恢复到109Ω.对于75℃、85%RH、450μg/cm2和10V偏置电压条件下的电路板样品,开始时,表面绝缘电阻稳定在109Ω左右,376min时,表面绝缘电阻突然下降到106Ω,并立即恢复,之后表面绝缘电阻发生多次陡降,1312min后,电路板的表面绝缘电阻降低到104Ω,形成稳定的绝缘失效.
|
图 2 3种实验条件下梳状电路板样品的表面绝缘电阻 |
用光学显微镜观察实验后的电路板样品如图 3所示,可见,在印制电路板上形成了明显的树枝状组织——晶枝.阳极的金属被氧化成阳离子,在电场力的作用下在电路板表面水膜中迁移至阴极,被还原成为金属原子,逐渐从阴极向阳极生长成树枝状金属沉积物——晶枝,这是产生电路板线间表面绝缘电阻下降的根本原因.表面绝缘电阻首次陡降,即电路板上晶枝首次形成两极之间的短路,此时晶枝细,电流通过后被击穿,如图 3(c)所示,故表面绝缘电阻马上恢复高阻值.之后电化学迁移不断发生,出现多次表面绝缘电阻陡降和恢复的现象,直到晶枝到达足够粗壮的状态,电路板表面绝缘失效不能恢复,如图 3(a)和(b)所示.但是在工程应用上,考虑到设备安全性问题,通常以表面绝缘电阻首次降到106Ω时所需时间为失效寿命.对于65℃、90%RH、550μg/cm2和20V条件下的电路板,失效寿命为85min;对于70℃、75%RH、650μg/cm2和15V条件下的电路板,失效寿命为498min;对于75℃、85%RH、450μg/cm2和10V条件下的电路板,失效寿命为376min.

|
图 3 温湿偏置实验后电路板样品晶枝形貌 |
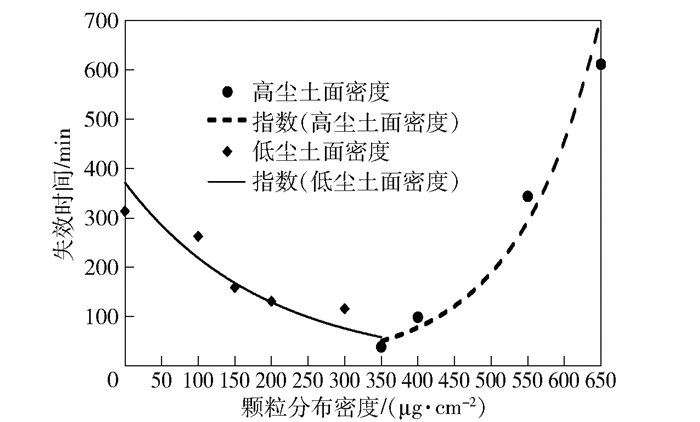
以85℃、93%RH、12V偏置电压、颗粒分布密度为0~650μg/cm2条件下的电路板电化学迁移失效时间曲线为例,讨论尘土颗粒分布密度对电路板电化学迁移失效时间的影响.电路板电化学迁移失效时间与尘土颗粒分布密度的关系如图 4所示,每个点为3次实验寿命数据威布尔拟合的特征寿命值.
|
图 4 电路板电化学迁移失效时间与颗粒分布密度的关系 |
电路板电化学迁移失效时间的变化随颗粒分布密度成非单调变化,存在以350μg/cm2为拐点的颗粒高、低分布密度区间,说明电路板表面发生绝缘失效的机理在颗粒高低密度区间存在差异.颗粒覆盖处于低密度区时,随颗粒密度增大,数量增多,靠毛细管作用颗粒与电路板交界处凝水量逐渐上升,为晶枝的生成提供了良好的环境,促进电化学迁移的发生.但是,当颗粒覆盖密度持续增大后,容易聚集形成不规则颗粒簇.这些颗粒簇反而阻碍了空气中的水分与电路板表面的接触,减少了离子迁移所必须的水溶液通路,且存在对晶枝生长的物理性阻挡,这样就会降低离子迁移速率,抑制了电化学迁移的发生.
2.3 颗粒分布密度与温湿偏置交互作用下的电路板电化学迁移失效寿命数据在表 1正交实验基础上又增加了93%RH、12V偏置电压,以及50μg/cm2、75μg/cm2、200μg/cm2、300μg/cm2颗粒分布密度等参数水平,共进行了52组4个影响因素的实验.每组实验条件下包含3次重复实验,以表面绝缘电阻首次降到106Ω所需时间为失效寿命,去除无效实验结果,共得到120个加速失效寿命实验数据.选择93组数据作为训练集,其中颗粒分布高密度区寿命数据39组,低密度区寿命数据64组,350μg/cm2密度下的数据在高、低密度区均使用. 27组数据作为测试集,其中颗粒分布高密度区寿命数据10组,低密度区寿命数据19组,350μg/cm2密度下的数据在高、低密度区均使用,测试集涵盖了绝大部分温湿偏置和颗粒密度实验条件,以提高评价的可行性,如表 2所示.
|
|
表 2 测试集 |
由于颗粒在电路板表面的分布状态是一种离散状态,难以建立温湿偏置交互作用下的电路板电化学迁移失效物理模型,进而考虑采用构建多项式进行统计回归的方法和机器学习中的RF、GBRT方法进行电路板电化学迁移失效的寿命预测.依据颗粒分布在高密度区间、低密度区间电化学迁移失效机理不同的研究结果,利用训练集分别在2个颗粒分布密度区建立颗粒影响下的电路板电化学迁移失效模型,并使用测试集进行评估.
3.1 模型评估方法不同失效寿命模型的准确性以NMSE来衡量. NMSE为模型预测性能和基准模型预测性能的比值,即
模型的预测性能与NMSE的值成反比,NMSE的值越小,模型预测性能越好[14].
3.2 多项式回归建模多项式回归需要分别建立自变量与因变量之间的多项式函数.由于温度、湿度、电压与失效时间均有基于失效物理的经验公式,只需利用训练集数据拟合出颗粒密度单一变量与失效时间之间的函数关系即可进行多项式建模.利用多项式回归建模可以最大效力地建立失效机理与统计模型的联系,进而提高寿命预测模型的准确度.颗粒分布密度对电路板寿命影响的模型如式(2)和式(3)所示,其中a~h均为常数.
低尘土密度为
| $ y = - a + bx + c{x^2} - d{x^3} $ | (2) |
高尘土密度为
| $ y = e - fx + g{x^2} - h{x^3} $ | (3) |
由于温度、湿度、电压和颗粒密度对电化学迁移失效的作用机理各不相同,可以将这4个参数视为独立影响因素进行相乘[10],根据训练集数据利用最小二乘法重新估算参数.求得温度x1、湿度x2、偏置电压x3、尘土密度x4与失效时间y的最优回归方程,颗粒分布低密度区寿命模型见式(4),高密度区寿命模型见式(5).
| $ \begin{array}{l} y = - 3{\kern 1pt} {\kern 1pt} {\kern 1pt} 529.68{{\rm{e}}^{\frac{{172.192}}{{{x_1}}}}} \times 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 366{\kern 1pt} {\kern 1pt} 450.233x_2^{ - 8.176} \times \\ 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 931.647x_3^{ - 0.491}( - 105{\kern 1pt} {\kern 1pt} {\kern 1pt} 169.61 + 483.439{x_4} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.002x_4^2 - 7.38 \times {10^{ - 6}}x_4^3) \end{array} $ | (4) |
| $ \begin{array}{l} y = 198{\kern 1pt} {\kern 1pt} {\kern 1pt} 863.76{{\rm{e}}^{\frac{{140.357}}{{{x_1}}}}} \times 161{\kern 1pt} {\kern 1pt} {\kern 1pt} 352{\kern 1pt} {\kern 1pt} {\kern 1pt} 148.191x_2^{ - 9.877} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6{\kern 1pt} {\kern 1pt} {\kern 1pt} 742.123x_3^{ - 0.444}(10{\kern 1pt} {\kern 1pt} {\kern 1pt} 933.109 - 65.239{x_4} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.125x_4^2 - 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 052{\kern 1pt} {\kern 1pt} {\kern 1pt} 66x_4^3) \end{array} $ | (5) |
使用测试集数据进行评估,颗粒分布低密度区寿命模型的NMSE为0.336,高密度区寿命模型的NMSE为0.399,误差较大.
3.3 机器学习建模机器学习中的GBRT和RF都属于集成学习,即通过整合多个弱分类器为一个强分类器.集成学习与一种有放回的抽样方法“Bootstrap”密切相关. “Bootstrap”是用原样本自身的数据抽样得出新的样本及统计量,进而估计数据的真实分布.它是现代统计学较为流行的一种统计方法,在小样本时效果很好,这比较符合电路板电化学迁移失效数据较少的情况. Bootstrap可以分为Bagging和Boosting 2种,虽然都是有放回的抽样,但二者的区别在于:Bagging采用有放回的均匀取样,而Boosting根据错误率来取样,因此Boosting的分类精度要优于Bagging.
1) GBRT算法预测电路板电化学迁移寿命
GBDT是Boosting算法的改进,即从弱学习算法出发,反复学习,得到一系列弱分类器(又称为基本分类器,为决策树),然后组合这些弱分类器,构成一个强分类器.提升方法实际上是采用加法模型(基函数线性组合)与前向分类算法的决策方法.相对于提升树而言,梯度提升树适用于一般损失函数. GBRT为GBDT对应的回归算法,算法如下[15].
输入:训练数据集,
| $ \begin{array}{*{20}{c}} {T = \{ ({x_1},{y_1}),({x_2},{y_2}), \cdots ,({x_N},{y_N})\} ,}\\ {{x_i} \in \chi \subseteq {{\bf{R}}^n},{y_i} \in y \subseteq {\bf{R}}} \end{array} $ |
损失函数L(y, f(x))
输出:回归树
① 初始化
| $ {f_0}(x) = {\rm{arg}}\mathop {{\rm{min}}}\limits_c \sum\limits_{i = 1}^N L ({y_i},c) $ | (6) |
② 对m=1, 2, …, M,有
a) 对i=1, 2, …, N,计算
| $ {r_{mi}} = - {\left\{ {\frac{{\partial L[{y_i},f({x_i})]}}{{\partial f({x_i})}}} \right\}_{f(x) = {f_{m - 1}}(x)}} $ | (7) |
b) 对rmi拟合一个回归树,得到第m棵树的叶结点区域Rmj,j=1, 2, …, J.
c) 对j=1, 2, …, J,计算
| $ {c_{mj}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_c \sum\limits_{{x_i} \in {R_{mj}}} L [{y_i},{f_{m - 1}}({x_i}) + c] $ | (8) |
d) 更新
| $ {f_m}(x) = {f_{m - 1}}(x) + \sum\limits_{j = 1}^J {{c_{mj}}} I(x \in {R_{mj}}) $ | (9) |
③ 得到GBRT模型,有
| $ \hat f(x) = {f_M}(x) = \sum\limits_{m = 1}^M {\sum\limits_{j = 1}^J {{c_{mj}}} } I(x \in {R_{mj}}) $ | (10) |
其中:M为树的个数,J为每棵树叶结点区域个数,cmj为此叶结点区域损失函数最小值,Rmj为第m棵树的叶结点区域,I为指示函数,
GBRT核心在于每一次的计算都是为了减小上一次的残差,即在残差减小的梯度方向上建立一个新模型,从而根据梯度下降法使残差最小. GBRT能够根据数据的特点调整其结构,从而能够很好地拟合函数的关系. GBRT算法作为一种集成算法,继承了决策树算法的优点.同时,与单一决策树算法相比,它也能有效避免过拟合问题. GBRT被认为是统计学习性能中最好的方法之一[13].
GBRT算法预测电路板电化学迁移寿命,颗粒分布低密度区模型的NMSE为0.013,高密度区模型的NMSE为0.236,较多项式模型预测准确度均有所提高,且在颗粒低分布密度区的预测效果提高更显著.
2) RF算法预测电路板电化学迁移寿命
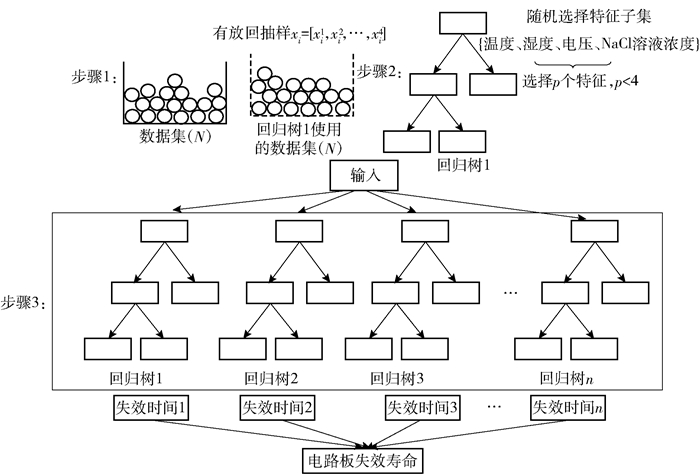
RF是以决策树为基础的分类器算法,它是Bagging算法的代表. RF算法分为3个步骤:第1步,有放回地随机抽取N个样本;第2步,在抽取的N个样本中随机选取p个特征,并建立决策树;第3步,重复1、2步,直到独立地建立n个决策树集合,再构成RF. RF可用于处理回归、分类、聚类以及生存分析等问题.当用于分类或回归时,其主要思想是通过自助法重采样,生成很多个树回归器或分类器.当数据中噪声或分裂属性过多时,RF算法可以解决树不平衡问题和对训练集的过度拟合问题.该方法同样被认为是统计学习性能最好的方法之一,如图 5所示[16].
|
图 5 RF结构 |
RF算法预测电路板电化学迁移寿命,颗粒分布低密度区模型的NMSE为0.034,高密度区模型的NMSE为0.196,较多项式模型预测准确度均有所提高,且在颗粒分布低密度区的预测效果提高更显著,而在高密度区的预测效果比GBRT更好.
4 讨论 4.1 尘土不可溶颗粒对电路板电化学迁移的作用特性尘土不可溶颗粒在电路板表面的沉积会增加表面水分的含量,为离子迁移提供了水溶液的通道,促进电化学迁移失效.但是,当颗粒覆盖密度持续增大后,容易聚集形成颗粒簇,反而阻碍了空气中的水分与电路板表面的接触,减少了离子迁移所必须的水溶液通路,且颗粒对离子迁移和晶枝生成的物理性阻挡越来越强,这样就会降低离子迁移速率,延缓晶枝生长.因此,随着尘土中不溶性颗粒覆盖密度由低到高,电路板电化学迁移失效寿命呈非单调变化趋势,存在以350μg/cm2为拐点的颗粒高、低分布密度区间.
4.2 不可溶颗粒影响下电路板电化学迁移寿命建模针对难以建立不可溶颗粒作用下的电路板电化学迁移失效物理模型的情况,在高、低颗粒分布密度区间分别利用多项式回归、GBRT、RF 3种方法建立电路板电化学迁移寿命预测模型,3种方法的NMSE比较如表 3所示.结果表明,GBRT方法在颗粒低分布密度区间的预测效果较好,RF方法在颗粒高分布密度区间的预测性能较好,机器学习建模方法优于多项式回归方法.
|
|
表 3 3种建模方法的NMSE值 |
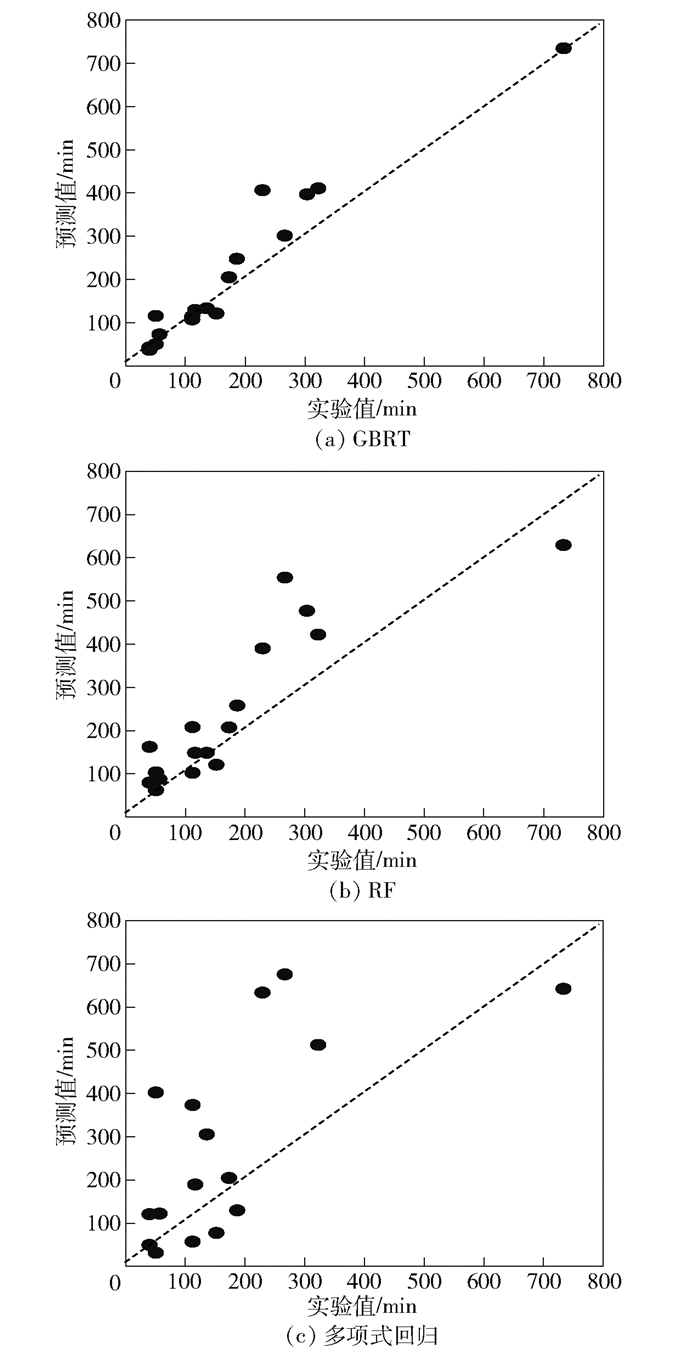
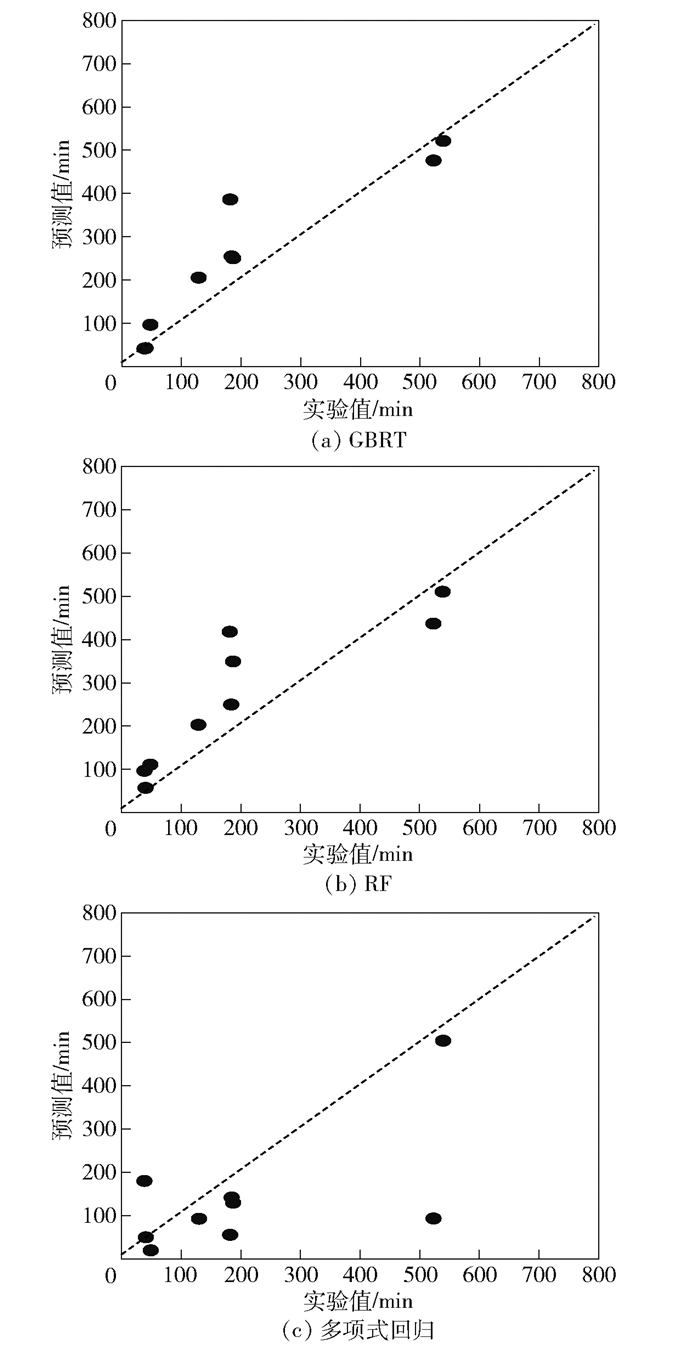
图 6、图 7分别显示了3种模型在颗粒低、高分布密度区间的预测性能.其中,横坐标为实验失效时间,纵坐标为预测失效时间.图中虚线上的点表示实验值与预测值相等的情形.数据离虚线越近,表示模型的预测值越接近实验值,即模型的预测性能越好.在颗粒低分布密度区间,可以直观地发现GBRT模型的预测性能最好.在颗粒高分布密度区间,可以直观地发现RF模型的预测性能最好.整体而言,利用机器学习方法的建模效果比利用多项式回归方法显著.
|
图 6 颗粒低密度区电路板电化学迁移寿命回归模型预测性能 |
|
图 7 颗粒高密度区电路板电化学迁移寿命回归模型预测性能 |
在温度、湿度、偏置电压、不可溶颗粒分布密度4个条件参数较温和时,即电路板电化学迁移失效时间较长的情况下,实验测得的电化学迁移失效时间离散性较大,所以基于多项式回归建模误差较大.但是,GBRT和RF模型预测误差较小.这是由于GBRT、RF作为集成学习的方法,其自我学习能力极好,在数据量有限的情况下通过迭代可有效处理数据的异常值,而多项式回归模型在预测离散性较大的数据时效果不好.
5 结束语严重的尘土污染给高密度电路板的电化学迁移失效带来了很大的风险.研究尘土颗粒分布与温度、湿度、偏置电压交互作用下对电路板电化学迁移失效机理的影响,建立基于电化学迁移失效的电路板寿命预测模型具有重要意义.通过温湿偏置加速实验,模拟不同积尘密度下电路板的电化学迁移失效,发现由于尘土不可溶颗粒在电路板表面的分布密度会改变表面水分的吸附量以及对离子迁移和晶枝生成的物理性阻挡程度,导致随尘土颗粒覆盖密度的由低到高,电路板电化学迁移失效寿命呈非单调变化趋势,存在以350μg/cm2为拐点的颗粒高、低分布密度区间.
采用基于正交实验的多组尘土颗粒密度、温度、相对湿度、偏置电压交互条件下电路板绝缘失效的寿命数据,基于数据驱动的方法,对比了多项式回归、机器学习中的GBRT和RF 3种方法在尘土分布密度的高低区间内对电路板电化学迁移的寿命预测效果.结果表明,对于尘土颗粒高分布密度区,利用RF方法建立电路板电化学迁移失效模型效果较好;而对于低分布密度区,利用GBRT方法效果较好.整体而言,无论是颗粒低分布密度还是高分布密度,在寿命数据有限的情况下,机器学习建模方法在电路板电化学迁移寿命预测的准确度远优于多项式回归建模方法.
| [1] |
Kohman G T, Hermance H W, Downes G H. Silver migration in electrical insulation[J]. Bell System Technical Journal, 1955, 34(6): 1115-1147. DOI:10.1002/j.1538-7305.1955.tb03793.x |
| [2] |
Zhang Jigao. Effect of dust contamination on electrical contact failure[C]//53th IEEE Holm Conference on Electrical Contacts. Pittsburgh: [s. n.], 2007: 21-30.
|
| [3] |
周怡琳, 韦霞霞. 尘土污染对电路板表面湿度的影响[J]. 电工技术学报, 2015, 30(23): 163-168. Zhou Yilin, Wei Xiaxia. Effects of dust contamination on surface relative humidity of printed circuit board[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 163-168. |
| [4] |
周怡琳, 朱蒙, 霍雨佳. 尘土颗粒的介电特性对电路板电化学迁移的影响[J]. 电子学报, 2017, 45(7): 1758-1763. Zhou Yilin, Zhu Meng, Huo Yujia. The influence of the dielectric properties of dust particles on electrochemical migration of printed circuit board[J]. Acta Electronica Sinica, 2017, 45(7): 1758-1763. |
| [5] |
Giulio D. Metal migration(Ag, Cu, Pb) in encapsulated modules and time-to-fail model as a function of the environment and package properties[C]//20th International Reliability Physics Symposium. San Diego: [s. n.], 1982: 27-33.
|
| [6] |
Yang S, Christou A. Failure model for silver electrochemical migration[J]. IEEE Transactions on Device and Materials Reliability, 2007, 7(1): 188-196. DOI:10.1109/TDMR.2007.891531 |
| [7] |
Zhou Yilin, Chen Yanyu, Xie Qi, et al. Modeling research of electrochemical migration failure on printed circuit board[C]//Prognostics and System Health Management Conference. Chongqing: [s. n. ], 2018: 26-28.
|
| [8] |
Tremblay G, Legendre P, Jean François Doyon, et al. The use of polynomial regression analysis with indicator variables for interpretation of mercury in fish data[J]. Biogeochemistry, 1998, 40(2/3): 189-201. DOI:10.1023/A:1005997430906 |
| [9] |
Zhou Sanyu. An exact method for the multiple comparison of several polynomial regression models with applications in dose-response study[J]. Advances in Statistical Analysis, 2018, 102(3): 413-429. |
| [10] |
谢琪.尘土中可溶性盐导致高密度电路板电化学迁移失效的建模研究[D].北京: 北京邮电大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10013-1018096618.htm
|
| [11] |
Wu Dazhong, Connor Jennings, Janis Terpenny, et al. A comparative study on machine learning algorithms for smart manufacturing: tool wear prediction using random forests[J]. Journal of Manufacturing Science & Engineering, 2017, 139(7): 071018-1. |
| [12] |
Wang Jidong, Li Peng, Ran Ran, et al. A short-term photovoltaic power prediction model based on the gradient boost decision tree[J]. Applied Sciences, 2018, 8(5): 689-702. DOI:10.3390/app8050689 |
| [13] |
IPC. Electrochemical migration resistance test: IPC TM-6502.6.14.1-2000[S]. [S.l.]: US-IPC, 2000.
|
| [14] |
Zhao Yanchang. R语言与数据挖掘最佳实践和经典案例[M].陈健, 黄琰, 译.北京: 机械工业出版社, 2014: 267-289.
|
| [15] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 151-152.
|
| [16] |
谢晓龙.航空发动机性能评价与衰退预测方法研究[D].哈尔滨: 哈尔滨工业大学, 2016.
|


