2. 西安邮电大学 计算机学院, 西安 710121;
3. 西安邮电大学 陕西省网络数据分析与智能处理重点实验室, 西安 710121
针对复杂场景下目标容易丢失的问题,提出了一种基于深度残差网络(ResNet)特征的尺度自适应视觉目标跟踪算法.首先,通过ResNet提取图像感兴趣区域的多层深度特征,考虑到修正线性单元(ReLU)激活函数对目标特征的抑制作用,在ReLU函数之前选取用于提取目标特征的卷积层;然后,在提取的多层特征上分别构建基于核相关滤波的位置滤波器,并对得到的多个响应图进行加权融合,选取响应值最大的点即为目标中心位置.目标位置确定后,对目标进行多个尺度采样,分别提取不同尺度图像的方向梯度直方图(fHOG)特征,在此基础上构建尺度相关滤波器,从而实现对目标尺度的准确估计.在视频集OTB100中与其他6种相关算法进行了比较,实验结果表明,所提算法取得了较高的跟踪成功率和精确度,能够较好地适应目标的尺度变化、背景干扰等复杂场景.
2. School of Computer Science and Technology, Xi'an University of Posts and Telecommunications, Xi'an 710121, China;
3. Shanxi Key Laboratory of Network Data Analysis and Intelligent Processing, Xi'an University of Posts and Telecommunications, Xi'an 710121, China
Because the objects are easy to be lost in complex scenes, a scale adaptive visual object tracking algorithm based on deep residual network (ResNet) features is proposed. Firstly, the ResNet is used to extract the multi-layer deep features of the image region of interest. Considering the restraining effect of rectified linear units (ReLU) activation function on target features, only the convolutional layers before ReLU function are selected. Secondly, the translation filters based on kernelized correlation filter are constructed in the extracted multi-layer features, and then the weighted fusion of the multiple response maps is carried out to obtain the target position with the largest response value. After the target location is determined, the target is sampled at multiple scales, and the felzenszwalb histogram of oriented gradients (fHOG) features of different scale images are extracted separately. On this basis, a scale correlation filter is constructed to estimate the target scale accurately. Comparing with six related algorithms in OTB100, an experiment is carried. It is shown that the proposed algorithm achieves high tracking success rate and accuracy, and can adapt to scale variation, background clutter and other complex scenes.
近年来,目标跟踪问题一直是计算机视觉领域研究的热点[1].根据观测模型不同,目标跟踪算法可分为生成式模型算法和判别式模型算法2类.典型的生成式模型算法有均值漂移、粒子滤波等.判别式模型算法如深度学习跟踪(DLT, deep learning tracker)、核相关滤波(KCF, kernelized correlation filter)、卷积神经网络-支持向量机(CNN-SVM, convolutional neural network-support vector machine)等,已经成为解决目标跟踪问题的主流方法.
Henriques等[2]提出的KCF算法,利用目标及其周围区域,通过构建循环矩阵采集正负样本,提取多通道方向梯度直方图(fHOG, felzenszwalb histogram of oriented gradients)特征,采用岭回归训练目标滤波器,并成功地利用循环矩阵在频域可对角化的性质将矩阵的运算转化为向量元素的点乘,大大降低了运算量,提高了运算速度,使算法能够满足实时性要求.但是,KCF算法没有考虑尺度变化,如果目标缩小,滤波器就会学习到大量背景信息,如果目标扩大,滤波器只学习了目标的局部纹理,这2种情况都很可能导致跟踪漂移. Ma等[3]提出的分层卷积特征(HCF, hierarchical convolutional features)算法,其基本框架就是KCF,不同的是HCF算法使用深度卷积网络特征.
判别式尺度空间跟踪(DSST, discriminative scale space tracker)算法[4]将目标跟踪看成目标中心平移和目标尺度变化2个独立问题,依据最小输出均方误差和(MOSSE, minimum output sum of squared error)算法中提出的相关滤波器(CF, correlation filter),进而设计了2个相互独立的CF,即位置滤波器和尺度滤波器,分别用于实现目标定位和尺度估计. Li等[5]提出的尺度自适应多特征(SAMF, scale adaptive multiple feature)算法,仍然基于CF框架,但是将单一特征扩展为多个特征,实现了灰度特征、方向梯度直方图(HOG)特征和颜色特征融合.
结合深度学习技术是目前目标跟踪算法的主要方向,如HCF[3]、CNN-SVM、全卷积孪生网络(SiamFC, fully-convolutional siamese networks)算法等. HCF算法通过预训练的网络模型VGG-19提取被跟踪目标的深度特征,利用CF确定目标位置. Hong等[6]提出的CNN-SVM算法,以卷积神经网络全连接层的输出为目标特征,结合在线支持向量机构建了目标跟踪模型. Bertinetto等[7]提出的SiamFC算法原理与CF很相似,都是通过比较搜索区域与目标模板的相似度,把相似度值最大的点作为新的目标中心,不同的是SiamFC算法采用卷积操作计算相似度值. SiamFC算法采用5个尺度,SiamFC-3s算法采用了3个尺度.
笔者受文献[3-4]的启发,同时考虑到深度残差网络(ResNet, deep residual network)[8]较强的特征表示能力,提出了一种基于ResNet深度特征的尺度自适应目标跟踪算法.
1 相关技术基础 1.1 ResNet卷积神经网络(CNN, convolutional neural network)是一种典型的深度神经网络,2012年以来先后出现了多个CNN模型,如AlexNet、ZFNet、GoogLeNet、VGGNet、ResNet、DenseNet等. He等[8]提出的ResNet结构,通过在网络中增加恒等映射,很好地解决了深度网络中梯度消失问题,使得网络性能能够在网络深度增加时得到进一步提升. ResNet层数可以选择18、34、50、101、152等.在综合考虑网络各层的特征表示能力以及计算量等因素基础上,笔者选取了ResNet-50结构(见图 1),该网络的卷积层分为5个部分,即Conv1、Conv2、Conv3、Conv4和Conv5,每部分包含数量不等的子部分(用小圆圈表示),子部分的数量依次为1、3、4、6、3.子部分进一步表示多个卷积操作,其中实心小圆圈包含4个卷积操作,空心小圆圈包含3个卷积操作.

|
图 1 ResNet-50结构 |
CF的基本思想是,设计一个滤波模板,下一帧中多个候选区域与该模板进行卷积运算,输出响应最大的区域即为目标区域. KCF通过引入核函数,将训练的滤波模板变为一个非线性二分类器,可以判别候选区域是目标还是背景.
核相关滤波器α可以表示为[2]
| $ \mathit{\boldsymbol{\hat \alpha }} = \frac{{\mathit{\boldsymbol{\hat y}}}}{{{{\mathit{\boldsymbol{\hat k}}}^{xx}} + \lambda }} $ | (1) |
其中:y为通过高斯函数构建的响应值,
如果选择高斯核,则kxx为
| $ \begin{array}{l} {\mathit{\boldsymbol{k}}^{xx}} = {\rm{exp}}\left( { - \frac{1}{{{\sigma ^2}}}({{\left\| {{\kern 1pt} \mathit{\boldsymbol{x}}{\kern 1pt} } \right\|}^2} + {{\left\| {{\kern 1pt} \mathit{\boldsymbol{x}}{\kern 1pt} } \right\|}^2} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{\mathscr{F}^{ - 1}}({{\mathit{\boldsymbol{\hat x}}}^*} \odot \mathit{\boldsymbol{\hat x}})} \right) \end{array} $ | (2) |
其中:exp表示指数函数,如果变量为矩阵,则对矩阵每个元素进行指数运算;‖·‖表示向量的2-范数;x为样本特征;
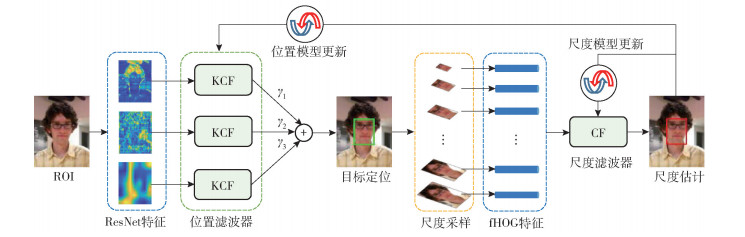
所提算法的总体结构如图 2所示,分为目标定位和尺度估计2个阶段,并利用跟踪结果对位置滤波器和尺度滤波器进行模型更新.
|
图 2 所提算法总体结构 |
假设输入图像中感兴趣区域(ROI, region of interest)大小为m×n×3,经过ResNet提取后,得到的特征大小分别为m1×n1×l1、m2×n2×l2和m3×n3×l3,li表示第i(i=1, 2, 3)个特征通道数.每个特征分别经过KCF,得到响应图大小均为s×t,然后对各个响应图加权求和,对应权值为γi,在融合后的响应图中值最大的点对应目标的中心位置.
所提算法在目标定位中,通过逐步增加特征层的数量,并经过大量实验验证,最终选择3层融合对目标特征进行表示,取得了较好的跟踪效果.
2.2.1 单层特征提取在ResNet-50中由低至高选择5层,分别为Conv1、Conv2-1、Conv3-1、Conv4-1和Conv5-1.在OTB100[9]上的测试结果显示,利用Conv4-1层提取的特征进行跟踪时,成功率和精确度均为最高.
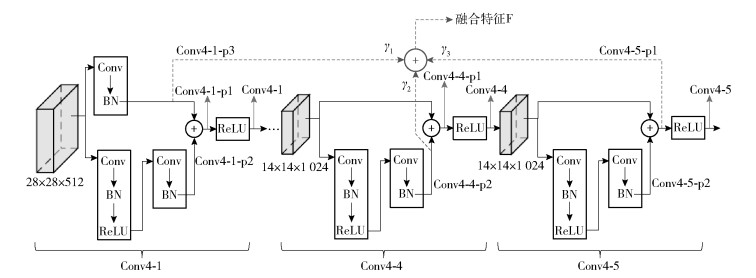
考虑到激活函数ReLU对目标特征的抑制作用,继续在Conv4-1之前的层Conv4-1-p1、Conv4-1-p2和Conv4-1-p3上进行测试,如图 3所示.综合考虑成功率和精确度可以看出,Conv4-1-p3取得了更好的跟踪效果,如表 1所示.
|
图 3 用于特征提取的ResNet层 |
|
|
表 1 ResNet不同层特征的跟踪效果对比 |
在Conv4内部,利用Conv4-1-p3与其他层融合进行测试(见图 3).
在OTB100上的测试结果(见表 2)表明,融合ResNet中Conv4-1-p3与Conv4-5-p1两层特征时,跟踪成功率和精确度均高于只提取一层特征Conv4-1-p3的跟踪结果.而且,与Conv4-5-p1融合的跟踪效果优于经过激活函数ReLU的Conv4-5层.
|
|
表 2 融合ResNet两个特征层的跟踪效果对比 |
为进一步提高深度特征的表示能力,在融合Conv4-1-p3和Conv4-5-p1基础上,尝试继续增加其他层.对跟踪结果中精确度比较低的视频进行了分析,并经过大量的实验验证,选定Conv4-1-p3、Conv4-4-p2和Conv4-5-p1三层(图 3中虚线标注)进行融合,跟踪效果得到进一步提升.图中“BN”表示批量归一化(batch normalization)操作.
实验过程中发现,三层特征融合时,采用不同的权重,跟踪效果不同,如表 3所示.因此,通过对跟踪权重进行优化,能获得更好的跟踪性能.实验中权重的取值被限制在0~1之间,通过大量实验得出的所提算法融合权重分别为γ1=1,γ2=0.2,γ3=1.
|
|
表 3 不同权重下的跟踪效果对比 |
权重取值相同时,对ReLU前后的层进行比较,由表 4可以看出,Conv4-1-p3、Conv4-4-p2和Conv4-5-p1三层融合时,取得了最好的跟踪效果,且这三层的位置均位于激活函数ReLU之前.
|
|
表 4 融合ResNet 3个特征层的跟踪效果对比 |
依据目标中心位置,进行尺度采样,得到33个不同尺度的样本,把所有样本变换成相同大小,分别提取每个样本的fHOG特征(共有d维). 33个特征向量,经过尺度滤波器,响应值最大的点对应当前帧中目标的精确尺度.
尺度滤波器表示为[4]
| $ {\mathit{\boldsymbol{H}}^l} = \frac{{{\mathit{\boldsymbol{G}}^*} \odot {\mathit{\boldsymbol{F}}^l}}}{{\sum\limits_{k = 1}^d {((} {\mathit{\boldsymbol{F}}^k}{)^*} \odot {\mathit{\boldsymbol{F}}^k}) + \lambda }} $ | (3) |
其中:G为利用高斯函数构建的响应值,G*表示G的共轭,Fl表示第l维特征的傅里叶变换,d为特征维数,λ为正则项.
尺度滤波器的分子项、部分分母项分别为
| $ {{\mathit{\boldsymbol{A}}^l} = {\mathit{\boldsymbol{G}}^*} \odot {\mathit{\boldsymbol{F}}^l}} $ | (4) |
| $ {\mathit{\boldsymbol{B}} = \sum\limits_{k = 1}^d {((} {\mathit{\boldsymbol{F}}^k}{)^*} \odot {\mathit{\boldsymbol{F}}^k})} $ | (5) |
响应值y为
| $ {\mathit{\boldsymbol{y}} = {\mathscr{F}^{ - 1}}\left( {\frac{{\sum\limits_{l = 1}^d {((} {\mathit{\boldsymbol{A}}^l}{)^*} \odot {\mathit{\boldsymbol{Z}}^l})}}{{\mathit{\boldsymbol{B}} + \lambda }}} \right)} $ | (6) |
y中最大值位置对应目标最佳尺度. Zl表示输入图像第l维特征的傅里叶变换.
2.4 模型更新确定第t帧图像中目标的位置和尺度后,为了使得跟踪算法更加鲁棒,需要在第t+1帧跟踪前对位置滤波器和尺度滤波器分别进行更新.
参照式(1),位置模型更新策略为
| $ {\mathit{\boldsymbol{\alpha }}_t} = (1 - \eta ){\mathit{\boldsymbol{\alpha }}_{t - 1}} + \eta \mathit{\boldsymbol{\alpha }}(t) $ | (7) |
其中:αt-1为对第t帧图像跟踪前求得的滤波器模板,α(t)为根据第t帧图像求得的滤波器模板,η为位置滤波器的学习率.
参照式(3),对第t帧图像跟踪后,尺度模型更新策略为
| $ {\mathit{\boldsymbol{A}}_t^l = (1 - {\eta ^\prime })\mathit{\boldsymbol{A}}_{t - 1}^l + {\eta ^\prime }\mathit{\boldsymbol{G}}_t^* \odot \mathit{\boldsymbol{F}}_t^l} $ | (8) |
| $ {{\mathit{\boldsymbol{B}}_t} = (1 - {\eta ^\prime }){\mathit{\boldsymbol{B}}_{t - 1}} + {\eta ^\prime }\sum\limits_{k = 1}^d {{{(\mathit{\boldsymbol{F}}_t^k)}^*}} \odot \mathit{\boldsymbol{F}}_t^k} $ | (9) |
其中η′为尺度滤波器的学习率.
3 实验结果分析 3.1 实验环境与参数选择在Windows 7系统下,采用Matlab和C++混合编程实现所提算法;硬件平台配置为:2块2.4GHz CPU,64GB内存,1块Nvidia GTX 1080Ti GPU.位置滤波器的学习率η=0.01,正则项λ=10-4.尺度滤波器的尺度因子a=1.02,采样个数S=33,学习率η′=0.025,正则项λ=10-4.
3.2 算法性能分析在视频集OTB100[9]中,选取具有尺度变化属性的64个视频进行测试.表 5、表 6详细列出了11种属性下算法的成功率和精确度,最优结果在表中用粗体标注,次优结果在表中用斜体表示.表头中字母缩写表示视频的不同属性,括号内值表示64个视频中具有对应属性的视频个数.可以看出,除了具有OV属性的视频集外,所提算法的成功率和精确度均为最优或次优.这主要是由于所提算法采用了具有较强特征表示能力的ResNet提取目标特征,同时考虑了目标尺度的变化.
|
|
表 5 不同属性下跟踪成功率对比 |
|
|
表 6 不同属性下跟踪精确度对比 |
综合以上分析,所提出的算法在具有尺度变化属性的视频集上表现出较好的综合跟踪性能,同时在光照变化、目标遮挡等复杂环境下仍然具有较好的鲁棒性.
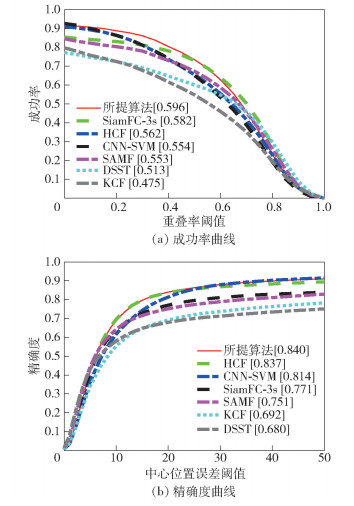
在OTB100的所有视频上对相关算法进行测试,成功率曲线和精确度曲线如图 4所示.
|
图 4 OTB100中所有视频的测试结果 |
与成功率位于第2的SiamFC-3s算法相比,所提算法的成功率和精确度分别提高了1.4%、6.9%;与精确度位于第2的HCF算法相比,所提算法的成功率和精确度分别提高了3.4%、0.3%.
3.3 算法速度对于不同的视频,目标的尺度不同,从而导致ROI大小不同.所提算法需要对ROI图像进行卷积等操作,因此目标尺度越大,算法速度越小.
在GPU加速下,所提算法在OTB100的所有视频上的平均速度为3.2f/s,与其他4种CF类算法速度比较如表 7所示.与HCF相比,导致所提算法速度较低的因素有2个:一是考虑了尺度变化,二是选用了层次更深的ResNet提取目标特征.
|
|
表 7 5种CF类算法跟踪速度比较 |
笔者提出了一种基于ResNet特征融合的尺度自适应目标跟踪算法.针对多层ResNet特征,利用KCF算法获得目标中心位置,然后对目标进行多尺度采样,在提取fHOG特征基础上利用CF对目标尺度进行精确估计.在视频集OTB100中对7种相关算法进行了测试,实验结果表明,所提算法能够准确提取目标特征,同时较好地适应目标尺度变化,取得了较高的跟踪成功率与精确度.但是,由于ResNet层数较多,降低了所提算法的跟踪速度.
在实验过程中发现,利用ResNet提取图像特征时,为了保证每个视频的跟踪结果均为最优,应该为不同视频选择不同的提取特征的层.如何做到针对每个视频进行自适应特征层选择,是所提算法进一步改进的方向.
| [1] |
卢湖川, 李佩霞, 王栋. 目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61-76. Lu Huchuan, Li Peixia, Wang Dong. Visual object tracking:a surey[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(1): 61-76. |
| [2] |
Henriques J F, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. |
| [3] |
Ma C, Huang J B, Yang X K, et al. Hierarchical convolutional features for visual tracking[C]//ICCV 2015. Santiago: Institute of Electrical and Electronics Engineers Inc., 2015: 3074-3082.
|
| [4] |
Danelljan M, Höger G, Khan F S, et al. Accurate scale estimation for robust visual tracking[C]//BMVC 2014. Nottingham: BMVA, 2014.
|
| [5] |
Li Y, Zhu J. A scale adaptive kernel correlation filter tracker with feature integration[C]//ECCV 2014. Zurich: Springer Verlag, 2014: 254-265.
|
| [6] |
Hong S, You T, Kwak S, et al. Online tracking by learning discriminative saliency map with convolutional neural network[C]//ICML 2015. Lile: IMLS, 2015: 597-606.
|
| [7] |
Bertinetto L, Valmadre J, Henriques J F, et al. Fully-convolutional siamese networks for object tracking[C]//ECCV 2016. Amsterdam: Springer Verlag, 2016: 850-865.
|
| [8] |
He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]//CVPR 2016. Las Vegas: IEEE Computer Society, 2016: 770-778.
|
| [9] |
田朗, 黄平牧, 吕铁军. SA-Siam++:基于双分支孪生网络的目标跟踪算法[J]. 北京邮电大学学报, 2019, 42(6): 105-110. Tian Lang, Huang Pingmu, Lü Tiejun. SA-Siam++:the two-branch siamese network-based object tracking algorithm[J]. Journal of Beijing University of Posts and Telecommunications, 2019, 42(6): 105-110. |


