随着实时在线游戏、虚拟现实等新兴计算密集型和时延敏感型应用业务的不断涌现，计算和能量资源受限的智能用户终端正面临着严峻挑战.为了缓解这一矛盾，满足用户业务高带宽、低时延、低能耗的服务需求，移动边缘计算(MEC，mobile-edge computing)技术已经演变为未来无线网络演进的一项关键技术^[1-2].区别于传统云计算，由于MEC允许用户直接将计算任务卸载至接入网络边缘的MEC服务器中，因此避免了日益严重的核心网络拥塞与漫长的任务传输时延问题.随着无线接入网络与MEC系统的深度融合，MEC将被赋予对无线网络参数的上下文感知能力，从而使得接入网络的通信资源与MEC服务器的计算资源的联合优化成为可能.时延和能耗是衡量任务卸载和计算效用的2大性能指标，任务在无线链路中的传输过程和在MEC服务器中的处理过程均会对这2种性能指标产生影响.因此，设计高效的通信和计算资源的联合优化算法是提升任务卸载与计算效用的关键^[3].

目前，学术界已有一些关于移动边缘计算网络中通信和计算资源联合优化的研究工作. Wang等^[4]分别以最小化任务完成时延和用户设备能耗为目标，通过联合优化用户设备计算频率和上行发射功率，探究了单个用户场景下的部分任务卸载问题. Mao等^[5]利用李雅普诺夫优化技术研究了能量收集场景中的电池容量与能量收集速率对任务完成时延的影响. Wu等^[6]以最小化任务完成时延为目标，通过联合优化任务卸载和上行发射功率，研究了非正交多址接入系统中的部分任务卸载问题. Chen等^[7]提出了一种基于深度增强学习的在线任务卸载和能量分配决策算法，以最小化长时期的任务完成时延和丢包率. Zhang等^[8]通过将用户的任务卸载过程建模为一个势博弈过程，提出了一个分布式的联合计算和通信资源分配算法.

与之前研究工作不同，通过以最大化用户任务卸载的时延增益和能耗增益为目标，提出了一种基于任务卸载增益最大化的时延和能耗均衡优化算法.通过联合优化MEC计算频率、用户上行发射功率以及子信道，最小化任务完成时间和用户能耗，从而使得移动边缘计算中的任务卸载增益最大化.

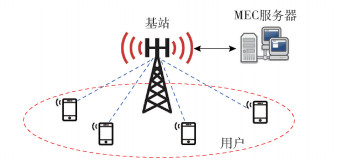
1 移动边缘计算任务卸载模型

考虑单个小区中MEC服务器服务多用户的场景，如图 1所示. MEC服务器部署在基站侧，为资源受限的移动用户终端提供计算任务卸载服务.假设每个用户通过正交频分多址(OFDMA，orthogonal frequency division multiple access)技术接入基站.用户集合采用$\mathscr{N} $ ={1，2，…，N}表示.整个系统频带被划分为K个子信道，用集合$ \mathscr{K}$ ={1，…，K}表示.定义子信道关联矩阵为x=[x_{n, k}]_N×K，其中

$ {x_{n,k}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{若用户 }}n{\rm{ 关联到子信道 }}k,}\\ {0,}&{{\rm{否则 }}} \end{array}} \right. $

(1)

为避免同信道干扰，假设每个子信道只能被分配给一个用户，即$\sum\limits_{n \in \mathscr{N}} x_{n, k} \leqslant 1, \forall k \in \mathscr{K} $.另外，假设每个用户最多分配到一个子信道，即$ \sum\limits_{k \in \mathscr{K}} x_{n, k} \leqslant 1, \forall n \in \mathscr{N} $.定义p=[p_n]_N为用户的上行发射功率向量，用户n到基站的最大上行传输速率可用香农公式表示为

$ {r_n} = \sum\limits_{k \in \mathscr{K}} {{x_{n,k}}} {B_k}{\rm{log}}(1 + {p_n}\varGamma _n^k) $

(2)

其中：$\mathit{\Gamma}_{n}^{k}=\left|g_{n, k}\right|^{2} / \sigma_{k}^{2} $表示基站接收端用户n在子信道k上的信号噪声比(SNR，signal to noise ratio).

假设系统中的每个用户有一个计算任务需要处理，表示为$\mathscr{A} _{n} $(α_n，β_n)，其中α_n表示任务的总比特长度，β_n为任务执行完成所需要的CPU周期数.任务$\mathscr{A}_{n} $在移动终端计算时的本地计算时延和能量消耗可以分别表示为

$ {t_n^l = \frac{{{\beta _n}}}{{f_n^l}}} $

(3)

$ {e_n^l = \kappa {{(f_n^l)}^2}{\beta _n}} $

(4)

其中：κ为与CPU芯片结构相关的能量消耗因子^[4]，f_n^l为移动终端的本地计算频率.如果此任务在MEC服务器完成，则需要的上传时延和计算时延分别为

$ {t_n^{up} = \frac{{{\alpha _n}}}{{{r_n}}}} $

(5)

$ {t_n^s = \frac{{{\beta _n}}}{{f_n^s}}} $

(6)

其中f_n^s为MEC服务器分配给用户n的计算频率.因此，用户n的任务卸载所耗费的总时延为t_n^off=t_n^up+t_n^s，用户n的任务卸载所耗费的总能量为e_n^off=α_nε_np_n/r_n，其中ε_n为功率放大器效率因子.通常情况下，由于任务计算输出的比特长度要远小于任务计算输入的比特长度，所以省略了任务计算输出的下行传输时延和用户用于接收任务计算输出所耗费的能量^[8].

2 通信和计算资源联合分配算法 2.1 问题描述

以网络总的任务卸载增益最大化为目标，联合优化子信道、上行发射功率和MEC计算频率分配.首先，将任务卸载增益定义为任务在边缘计算相比在本地计算所节约的时延和能耗加权量，即

$ \mathscr{U}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},{\mathit{\boldsymbol{f}}^s}) = \sum\limits_{n \in \mathscr{N}} {\left( {\lambda _n^e\frac{{e_n^l - e_n^{{\rm{ off }}}}}{{e_n^l}} + \lambda _n^t\frac{{t_n^l - t_n^{{\rm{ off }}}}}{{t_n^l}}} \right)} $

(7)

其中: $\lambda_{n}^{e}, \lambda_{n}^{t} \in[0, 1], \lambda_{n}^{e}+\lambda_{n}^{t}=1 $为用户n对于时延增益和能耗增益的偏好因子，用户可以根据自身的剩余能量资源和任务时延要求灵活调节偏好因子，从而达到对2种性能指标的不同侧重. f^s=[f_n^s]_N表示MEC计算频率分配向量.

至此，网络任务卸载增益最大化问题可以由问题$\mathscr{P}_1$描述

$ \begin{array}{l} \begin{array}{*{20}{l}} {{\mathscr{P}_1}:\mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},{\mathit{\boldsymbol{f}}^s}} \mathscr{U}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},{\mathit{\boldsymbol{f}}^s})}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{. }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1}}:0 \le {p_n} \le p_n^{{\rm{max}}},\forall n \in \mathscr{N}} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\rm{C}}2:\sum\limits_{n \in \mathscr{N}} {{x_{n,k}}} \le 1,\forall k \in \mathscr{K}}\\ {{\rm{C}}3:\sum\limits_{k \in \mathscr{K}} {{x_{n,k}}} \le 1,\forall n \in \mathscr{N}}\\ {{\rm{C}}4:\sum\limits_{n \in \mathscr{N}} {f_n^s} \le f_s^{{\rm{max}}}} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\rm{C}}5 :f_n^s \ge 0,\forall n \in \mathscr{N}}\\ {{\rm{C}}6 :{x_{n,k}} \in \{ 0,1\} ,\forall n \in \mathscr{N},\forall k \in \mathscr{K}} \end{array} \end{array} $

(8)

其中:C1为用户的上行发射功率约束；C2、C3和C6保证了每个子信道分配的正交性以及用户的单信道接入约束；C4和C5为MEC计算频率分配约束.不难发现，问题$\mathscr{P}1$是一个非凸的混合整数规划问题^[9]，且其复杂度随着用户和子信道的数目成指数性增长.为了使问题可解，在下文中，通过分析问题$\mathscr{P}1$的结构，将该问题分解为2个相互独立的子问题，即联合子信道和功率分配子问题和MEC计算频率分配子问题，进而提出了一种最优的通信和计算资源联合分配算法.

2.2 求解方案

首先，重写问题$\mathscr{P}1$的目标函数为

$ \mathscr{U}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},{\mathit{\boldsymbol{f}}^s}) = \sum\limits_{n \in \mathscr{N}} {(\lambda _n^e + \lambda _n^t)} - \varLambda (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},{\mathit{\boldsymbol{f}}^s}) $

(9)

其中$\mathit{\Lambda}\left(\boldsymbol{x}, \boldsymbol{p}, \boldsymbol{f}^{s}\right)=\sum\limits_{n \in \mathscr{N}}\left(\frac{\lambda_{n}^{e} e_{n}^{\text {off }}}{e_{n}^{l}}+\frac{\lambda_{n}^{t} t_{n}^{\text {off }}}{t_{n}^{l}}\right) $.

式(9)中的第1项是一个常数项，去除第2项的负号，可以将任务卸载增益最大化问题$\mathscr{P}1$等价地转化为时延和能耗开销最小化问题$\mathscr{P}$2

$ \begin{array}{*{20}{c}} {\mathscr{P}2:\mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},{\mathit{\boldsymbol{f}}^s}} \varLambda (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},{\mathit{\boldsymbol{f}}^s})}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1,C2,C3,C4,C5,C6}}} \end{array} $

(10)

由于变量{x，p}和f^s在问题$\mathscr{P}$2的目标函数和约束中均可分，所以它可以被分解为2个独立的子问题，即联合子信道和功率分配子问题和MEC计算频率分配子问题.其中，联合子信道和功率分配子问题可以表示为

$ \begin{array}{*{20}{c}} {\mathscr{P}3:\mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}}} \sum\limits_{n \in \mathscr{N}} {\frac{{{\phi _n} + {\varphi _n}{p_n}}}{{\sum\limits_{k \in \mathscr{K}} {{x_{n,k}}} {B_k}{\rm{log}}(1 + {p_n}\varGamma _n^k)}}} }\\ {{\rm{ s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1,C2,C3,C6}}} \end{array} $

(11)

其中: $ \boldsymbol{\phi}_{n}=\lambda_{n}^{t} \alpha_{n} / t_{n}^{l}, \varphi_{n}=\lambda_{n}^{e} \varepsilon_{n} \alpha_{n} / e_{n}^{l}$.为了求解问题$\mathscr{P}$3，首先假设给定任务$\mathscr{A} _{n} $在子信道k上传输，即x_n，k=1.同时定义函数

$ {\vartheta _n}({p_{n,(k)}}) = \frac{{{\phi _n} + {\varphi _n}{p_{n,(k)}}}}{{{B_k}{\rm{log}}(1 + {p_{n,(k)}}\varGamma _n^k)}} $

(12)

其中p_n，(k)表示任务$\mathscr{A} _{n} $在子信道k上传输时的用户发射功率.在此条件下，问题$\mathscr{P}$3转变为求解N个相互独立的功率分配子问题$\mathscr{P}$4

$ \begin{array}{*{20}{l}} {\mathscr{P}4:\mathop {{\rm{min}}}\limits_{{p_n},(k)} {\vartheta _n}({p_{n,(k)}})}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{. }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {p_{n,(k)}} \le p_n^{{\rm{max}}}} \end{array} $

(13)

子问题$\mathscr{P}$4是一个非凸的分式规划问题，在求解其之前，首先给出如下引理.

引理1  问题$\mathscr{P}$4的目标函数是拟凸的，并且该问题存在唯一的全局最优解.

证明  类似证明可以参考文献[10].

根据引理1和一阶最优性条件，问题$\mathscr{P}$4的最优解p_n，(k)^*要么在约束边界取到，要么满足$ \vartheta_{n}^{\prime}\left(p_{n, (k)}^{*}\right)=0$，即

$ \begin{array}{*{20}{c}} {{\varOmega _n}({p_{n,(k)}}) = {\varphi _n}{\rm{log}}(1 + {p_{n,(k)}}\varGamma _n^k) - }\\ {\frac{{\varGamma _n^k({\phi _n} + {\varphi _n}{p_{n,(k)}})}}{{(1 + {p_{n,(k)}}\varGamma _n^k){\rm{ln}}{\kern 1pt} {\kern 1pt} 2}} = 0} \end{array} $

(14)

又因为Ω′_n(p_n，(k))>0，Ω_n(0) < 0，所以提出了一种基于二分法的高效功率分配算法.

算法1   基于二分法的高效功率分配算法

1 根据式(14)计算Ω_n(p_n^max)；

2 如果Ω_n(p_n^max)≤0则

3   p_n，(k)^*=p_n^max；

4 否则

5   初始化收敛容限τ；

6   设置辅助变量p′=0，p″=p_n^max；

7  重复

8    设p_n，(k)^*=(p′+p″)/2；

9    如果Ω_n(p_n，(k)^*)≤0则

10      设p′=p_n，(k)^*；

11    否则

12    设p″=p_n，(k)^*；

13  直到p″－p′≤τ

14  设p_n，(k)^*=(p′+p″)/2；

15 输出p_n，(k)^*；

将算法1中得到的最优功率分配p_n，(k)^*代入问题$\mathscr{P}$3，可以得到如下问题

$ \begin{array}{l} \mathscr{P}5:\mathop {{\rm{min}}}\limits_x \sum\limits_{n \in \mathscr{N}} {\sum\limits_{k \in \mathscr{K}} {{x_{n,k}}} } {\vartheta _n}(p_{n,(k)}^*)\\ {\rm{ }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C2,C3,C6}} \end{array} $

(15)

问题$\mathscr{P}$5是一个典型的二部图匹配问题，因而可以用经典的匈牙利算法进行高效求解^[11].

MEC计算频率分配子问题表示如下

$ \begin{array}{*{20}{l}} {\mathscr{P}6:\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{f}}^s}} \sum\limits_{n \in \mathscr{N}} {\frac{{{\eta _n}}}{{f_n^s}}} }\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C5,C6}}} \end{array} $

(16)

其中$\eta_{n}=\lambda_{n}^{t} f_{n}^{l} $.显然，问题$\mathscr{P}$6是一个具有线性不等式约束的凸优化问题，所以可以用Karush-Kuhn-Tucker(KKT)条件和拉格朗日乘子法^{[9, 12]}对其进行求解.具体地，引入拉格朗日乘子δ，问题$\mathscr{P}$6的拉格朗日函数可以表示为

$ \mathscr{L}({\mathit{\boldsymbol{f}}^s},\delta ) = \sum\limits_{n \in \mathscr{N}} {\frac{{{\eta _n}}}{{f_n^s}}} + \delta \left( {\sum\limits_{n \in \mathscr{N}} {f_n^s} - f_s^{{\rm{max}}}} \right) $

(17)

拉格朗日对偶函数表示为

$ \mathscr{G}(\delta ) = \mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{f}}^s} \ge 0} \mathscr{L}({\mathit{\boldsymbol{f}}^s},\delta ) $

(18)

问题$\mathscr{P}$6的对偶问题为$\max\limits_{\delta \geqslant 0} \mathscr{G}(\delta) $.通过KKT条件，可以得到$f_{n}^{*}=\sqrt{\eta_{n} / \delta}, \forall n \in \mathscr{N} $.将f_n^*代入拉格朗日对偶问题，求得拉格朗日乘子的最优值为

$ {\delta ^*} = {\left( {\sum\limits_{n \in N} {\sqrt {{\eta _n}} } /f_s^{{\rm{max}}}} \right)^2} $

(19)

因此最优MEC计算频率分配为

$ f_n^* = \frac{{\sqrt {{\eta _n}} f_s^{{\rm{max}}}}}{{\sum\limits_{n \in \mathscr{N}} {{\eta _n}} }},\forall n \in \mathscr{N} $

(20)

通过以上分析，可以获得每个用户在任务卸载时的最优发射功率、子信道和MEC计算频率.为了避免任意一个用户的任务卸载增益为负值，每个用户可以根据式(21)进行任务计算模式选择

$ {b_n} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{若 }}\mathscr{U}_n^*(\mathit{\boldsymbol{x}}_n^*,\mathit{\boldsymbol{p}}_n^*,f_n^*) > 0}\\ {0,}&{{\rm{若 }}\mathscr{U}_n^*(\mathit{\boldsymbol{x}}_n^*,\mathit{\boldsymbol{p}}_n^*,f_n^*) \le 0} \end{array}} \right. $

(21)

其中b=[b_n]_N为用户的任务计算模式选择向量，当b_n=1时，用户n采用MEC边缘计算模式；当b_n=0时，用户n采用本地计算模式. $ \mathscr{U}_{n}^{*}\left(\boldsymbol{x}_{n}^{*}, \boldsymbol{p}_{n}^{*}, f_{n}^{*}\right)$为用户n的最优任务卸载增益.

2.3 算法步骤

通过以上分析，提出了一种最优的联合通信和计算资源分配(JCCRA，joint communication and computation resource allocation)算法，有以下步骤.

1) 网络参数输入.初始化任务模型$\mathscr{A} _{n} $(α_n，β_n)、上行信道增益|g_{n, k}|²和噪声功率σ_k²、计算能量消耗因子κ、功率放大器效率因子ε_n、用户能耗和时延偏好因子λ_n^e和λ_n^t、本地计算频率f_n^l等网络参数.

2) 用户上行功率分配.采用算法1提出的二分法获得每个用户在每个子信道上的最优功率分配p_n，(k)^*.

3) 最优子信道分配.通过步骤2)获得的最优功率分配p_n，(k)^*，获得每个用户在每个子信道上的匹配权重$\vartheta_{n}\left(p_{n, (k)}^{*}\right) $，通过匈牙利算法进行最优的子信道分配.

4) 最优MEC计算频率分配.通过式(20)获得每个用户的最优MEC计算频率分配.

5) 任务计算模式选择.通过步骤2)~5)所获得的最优用户上行功率、子信道和MEC计算频率分配，计算每个用户的最优任务卸增益$ \mathscr{U}_{n}^{*}\left(\boldsymbol{x}_{n}^{*}, \boldsymbol{p}_{n}^{*}, f_{n}^{*}\right)$，通过式(21)进行任务计算模式选择.

6) 资源优化结果输出. (b^*，x_n^*，p_n^*，f^s，*).

2.4 算法复杂度分析

由于最优的MEC计算频率分配可由KKT条件闭式导出，所以提出的JCCRA算法的复杂度主要取决于联合子信道和功率分配，即步骤2)和3).

1) 功率分配.为了获取匹配权重$\vartheta_{n}\left(p_{n, (k)}^{*}\right) $，需要针对每个用户和子信道运用二分法求解最优功率分配p_n，(k)^*.二分法复杂度为O(lb(p_n^max/τ))，步骤2)总的复杂度为$ O\left(\sum\limits_{n \in N} K \operatorname{lb}\left(p_{n}^{\max } / \tau\right)\right)$.

2) 子信道分配.由文献[11]可知，运用匈牙利算法进行子信道分配的复杂度为$O\left(N K^{2}+N \log N\right) $.

结合1)和2)，JCCRA算法总的复杂度为$ O\left(\sum\limits_{n \in N} K \operatorname{lb}\left(p_{n}^{\max } / \tau\right)+N K^{2}+N \log N\right)$.不难看出，JCCRA算法的计算复杂度为多项式复杂度，可适用于用户数目比较多的场景中.

3 仿真结果

不失一般性，考虑一个半径为1km的圆形服务区域，基站和MEC服务器同时部署在圆心，N个用户均匀分布在该服务区域内.假设每个用户具有相同的任务需要计算，任务模型为α_n=5×10⁵bit，β_n=1×10⁹CPU周期.用户到基站的路径损耗模型采用L=128.1+37.6lbddB，阴影衰落服从均值为零，方差为8dB的对数正态分布^[13].设置子信道的数目和用户数目相同，并设置系统总的带宽为20MHz，则每个子信道的带宽为B_k=20/KMHz.仿真中所用到的其他参数如下：κ=1×10^－26、ε_n=1/0.2、f_n^l=1×10⁹Hz、f_s^max=20×10⁹Hz、p_n^max=23dBm、σ_k²=－100dBm.

为了评估算法性能，分别采取2个对比算法与所提算法JCCRA进行比较，即基于最大SNR匹配的子信道分配算法(maxSNR)和基于穷举的最优子信道分配算法.在maxSNR算法中，每个用户采用最大发射功率传输，并采用基于最大SNR匹配的方式接入子信道；在穷举算法中，系统将采用穷举的方式进行最优子信道分配.

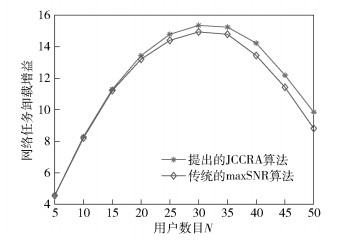
图 2说明了网络任务卸载增益随系统用户数目增大时的变化趋势.本次仿真中，将每个用户的偏好因子设置为λ_n^t=0.3和λ_n^e=0.7.从图中可以看出，提出的JCCRA算法在性能上明显优于maxSNR算法.观察到2种算法曲线均随用户数目的增多先上升后下降.这是因为当用户数目比较少时，网络的频谱资源和计算资源竞争不激烈，因而用户的增多可以增加任务卸载增益.然而当用户增加到一定数目时，网络资源变得紧缺，进而造成更大的任务卸载时延和能量消耗，使得任务卸载增益下降.

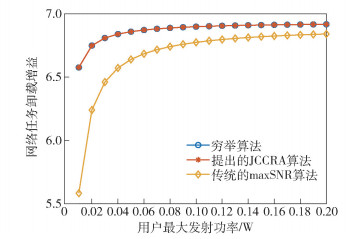
图 3说明了网络任务卸载增益随用户最大发射功率增大时的变化趋势.本次实验中，同时比较穷举算法、提出的JCCRA算法和传统的maxSNR算法的性能.由于穷举算法的复杂度极高，故将用户数目设置为N=8，每个用户的偏好因子设置为λ_n^t=0.3和λ_n^e=0.7.从图中可以看出，提出的JCCRA算法和最优的穷举算法性能基本相同，且3种算法的曲线均随用户最大发射功率增大而上升.这是因为用户最大发射功率的增大使得每个用户有更多的机会采取最优的发射功率进行传输，从而降低时延和能量开销，进而增大网络任务卸载增益.

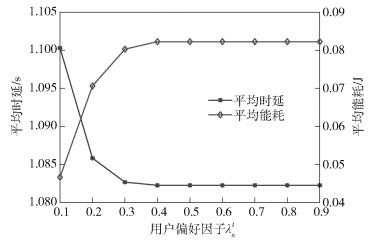
图 4说明了网络平均时延和平均能耗随用户偏好因子变化时的均衡趋势.在本次仿真中，将用户数目设置为N=20，同时设λ_n^e=1－λ_n^t.从图 4中可以看出，随着用户对时延偏好的增加，网络的平均时延逐渐减小，而网络的平均能耗逐渐增大，同时当用户的时延偏好因子λ_n^t≥0.4时，网络的平均时延和平均能耗开始保持稳定.这是因为，当λ_n^t数值比较小时，λ_n^t的增大使得系统以牺牲能耗性能来降低时延，然而当λ_n^t数值比较大时，由于用户的发射功率限制，继续增大λ_n^t并不能使得系统平均时延降低和平均能耗增大.

4 结束语

由于在移动边缘计算任务卸载的过程中，任务的卸载过程和计算过程会受到资源受限的上行信道和MEC服务器的双重挑战，从而产生额外的时延和能量开销.为缓解这一矛盾，提出了一种基于任务卸载增益最大化的联合通信和计算资源分配算法.通过联合优化用户上行发射功率、子信道分配和MEC计算频率，导出了针对每个用户的最优任务卸载增益，从而指导用户进行任务计算模式的选择.仿真结果表明，提出的算法在性能上要优于传统对比算法.