2. 中国空间技术研究院 西安分院, 西安 710000
面向星座式低轨(LEO)卫星网络,针对动态路由技术重构时间长导致的资源利用率下降问题,提出了一种基于预测的路径切换机制.依据卫星飞行轨迹,预测星间链路的可用时间,从而判断当前传输路径的可用寿命.在当前路径断开之前及时触发路由重构,为当前传输寻找备用路径,避免路由重构导致传输中断.提出了新型路径选择方案,根据当前路径代价和网络全局负载状态设计了综合代价函数,用于选择最优路径.仿真结果表明,所提出的路径切换技术可有效降低数据转发的丢包率,提升网络整体吞吐量.
2. China Academy of Space Technology(Xi'an), Xi'an 710000, China
For constellation low earth orbit (LEO) satellite networks, aiming at the problem of resource utilization decline caused by long reconfiguration time of dynamic routing technology, a path switching mechanism based on prediction is proposed. According to the satellite flight trajectory, the duration of inter-satellite link is predicted, so the available lifetime of the current transmission path can be estimated. With the proposed routing strategy, the route reconfiguration is initiated in time before the current path is disconnected, therefore. The transmission interruption by changing to another newly established path can be avoided. Moreover, according to the current path cost and the global load state of the network, a path cost metric is designed to select an optimal path. Simulations show that the proposed routing scheme can effectively reduce the packet loss rate of data forwarding and improve the overall throughput of the network.
随着空间信息技术的高速发展,卫星网络在全球通信、导航定位、气象预测、灾害监测和军事应用等方面发挥着越来越重要的作用,以卫星网络为核心的空间网络平台逐渐成为各国研究的重点战略性工程[1-2].地面网络由于其自身的特点,会受到地理条件、自然灾害等多种因素的限制,在这种情况下,具有全球无缝通信能力的卫星网络必将成为下一代互联网的关键组成部分[3].
当前低轨(LEO)卫星网络的路由机制主要分为静态路由和动态路由2种[4].静态的路由方案一般以虚拟拓扑、虚拟节点等策略为依托,屏蔽卫星网络的动态特性,将其分解为多个静态的场景并逐一进行路由的计算,例如在卫星网络中常见的“快照”机制就是典型的静态路由方案.采用静态路由策略可以减少路由建立和维护过程中带来的信令开销,但是在网络的负载均衡方面表现较差,很容易造成网络拥塞.
低轨卫星网络中的动态路由策略一般根据网络的拓扑变化进行动态的路由更新与维护,寻找当前网络中的最佳路径信息[5-6].采用动态路由策略可以降低网络拥塞概率,实现负载均衡,有效提升网络资源利用率.但是由于极轨道星座的特殊性质,卫星运行到极地区域时会被迫中断与异轨道星间链路,这一特性使得动态路由策略存在路径切换问题.一方面,链路进行切换的过程中,大量的路由寻路信息会导致网络中的信令负载过重,造成网络拥塞;另一方面,卫星重路由延迟大,大量数据可能丢失,从而降低网络利用率[7-8].
针对低轨卫星网络的路径切换问题,已有相关的研究成果[8-14]. Meng等[8]提出了一种基于路径剩余时间的星间路径切换方案,根据卫星运动周期性确定链路的断链时间,对数据包的发送时延和链路剩余时间进行比较,如果不能在链路断开之前完成数据的传输,则提前进行路径的切换. Werner等[9]研究了卫星网络的重路由问题,优化了路由算法,在数据发送方与接收方之间找到了一条在链路断链后路径切换代价最小的路径,该算法最小化了卫星路径切换的代价. Uzunalioglu[10]提出了一种概率路由协议,通过在寻找路由时剔除生存时间内可能进行路径切换的所有链路,以减少链路重路由的次数.文献[11-14]中讨论了静态路由的路径切换问题.以上工作都采用了断链再切换的方案,存在数据传输被中断的情况,因此,无法保证数据可靠传输.
为了解决低轨卫星网络动态路由策略中的路径切换问题,笔者提出了一种拓扑探测与数据转发并行的路径切换方案,打破了传统动态路由机制中链路断链重连的模式,在路径完全失效前完成路由的重构,并根据节点的业务负载能力选择最佳的切换方案,在保证路径持续可用的同时提升网络的负载均衡能力.
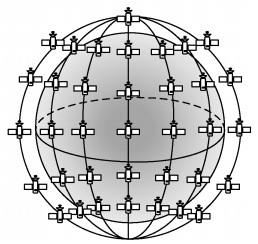
1 系统模型研究场景如图 1所示.定义网络中卫星的总数量为n,轨道面数量为P,且忽略不同轨道面的相位差.由于轨道倾角对所提方案影响较小,选用90°倾角的理论模型进行后续的分析与仿真.
|
图 1 极轨道星座场景图 |
使用图G={V, E}表示卫星网络的拓扑情况,其中V为网络中所有卫星节点的集合,则
| $ V = \{ {N_1},{N_2}, \cdots ,{N_n}\} $ | (1) |
E为网络中所有边的集合,表示为
| $ E = \{ ({N_i},{N_j})|1 \le i \le n,1 \le j \le n\} $ | (2) |
将网络使用图模型表示之后,用邻接矩阵表示网络的连接状况,设邻接矩阵为
| $ \mathit{\boldsymbol{A}} = ({a_{ij}})1 \le i \le n,1 \le j \le n $ | (3) |
| $ {a_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{ 当节点 }}{N_i}{\rm{ 和}}{N_j}{\rm{ 之间存在物理链路 }}}\\ {0,}&{{\rm{其他}}} \end{array}} \right. $ | (4) |
其中:i为行号,j为列号.
设在图G中从节点Ni到节点Nj的路由为pij,用节点序列表示为
| $ {p_{ij}} = \{ {N_i},{N_{{p_1}}},{N_{{p_2}}}, \cdots ,{N_{{p_l}}},{N_j}\} $ | (5) |
其中p1, p2, …, pl为路径经过的节点的下标.
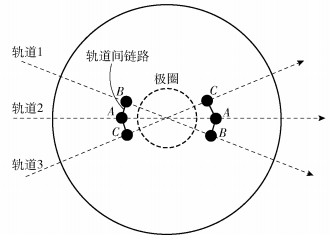
2 路径切换方案 2.1 路径切换条件在极轨道星座场景下,卫星通过星间链路与其他卫星相连接.在这些星间链路中,轨道内链路连接为固定连接,在运行周期内一直保持连接状态不会中断,但是轨道间链路会由于左右天线交替的原因在南北极圈处周期性地断链重连.如图 2所示,在卫星A穿过南北极区时,原本连接在其运行方向左侧的卫星B会移动到其运行方向右侧,原本连接在其运行方向右侧的卫星C会移动到其运行方向左侧,因此链路A-B和链路A-C都会在极区内断链而在离开极区时重连.
|
图 2 极区链路切换示意图 |
针对以上问题,提出了一种周期性的链路预测算法,通过对比链路可用时间与重路由时间,以此判断是否触发路径切换.
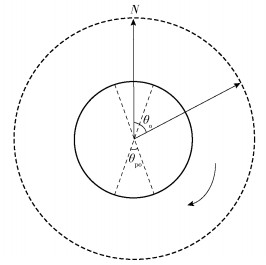
1) 链路的可用时间tc.卫星节点周期性地根据当前位置信息预测下一次到达极圈边界的时间,该时间为其相应轨道间链路的可用时间.如图 3所示,设卫星当前所在位置与北极的夹角为θo,南北极圈范围为θpo,由于卫星运行周期固定为T,下一次卫星进入极区的时间,也就是当前轨道间链路的可用时间为
| $ {t_c} = \left\{ {\begin{array}{*{20}{l}} {\frac{{2\pi - {\theta _{{\rm{po}}}} - 2{\theta _{\rm{o}}}}}{{4\pi }}T,}&{\frac{{{\theta _{{\rm{po}}}}}}{2} < {\theta _{\rm{o}}} < \frac{{2\pi - {\theta _{{\rm{po}}}}}}{2}}\\ {\frac{{4\pi - {\theta _{{\rm{po}}}} - 2{\theta _{\rm{o}}}}}{{4\pi }}T,}&{\frac{{2\pi + {\theta _{{\rm{po}}}}}}{2} < {\theta _{\rm{o}}} < \frac{{4\pi - {\theta _{{\rm{po}}}}}}{2}} \end{array}} \right. $ | (6) |
|
图 3 链路呵用时间计算示意图 |
2) 路由源节点的重路由时间tr.路由的重建包括中间节点反馈源节点路径中断的过程,以及源节点发起的完整寻路过程.若相邻节点间的最长传播时间为tmax,T,单一节点的排队时延为tavg,当前网络中路径的最大跳数为m,则最大重路由时间设为
| $ 3(m - 1)({t_{{\rm{max}},T}} + {t_{{\rm{avg}}}}) $ | (7) |
3) 路径切换条件.从卫星脱离极区开始计时,其异轨道链路可用时间在半周期内第1次小于(或等于)源节点的重路由时间时,则需要进行路径切换.
需要说明的是,该预测方法仅针对处于数据传输过程中的卫星节点,并且其异轨道邻居节点是其传输路径上的上一跳或者下一跳.若当前节点没有进行数据传输,或者其异轨道邻居节点不是数据传输路径的上一跳或者下一跳,那么该节点将不会进行预测,避免增加网络开销.
2.2 路径切换流程定义(链路状态E和路由状态R)若链路的可用时间小于当前路由的重路由时间,当前的链路状态称之为危险链路状态;否则为正常链路状态,表示为
| $ \mathit{\boldsymbol{E}}\left( {{p_{ij}}} \right)\left\{ \begin{array}{l} 1,{\rm{危险链路状态}}\\ 0,{\rm{正常链路状态}} \end{array} \right.\ \ \ \ \ \ \ \ ,i \ne j{\rm{且}}{c_i} = 1 $ | (8) |
当链路状态为危险状态时,为了保证新建立路径的有效性,该链路只能进行数据的传输而无法进行信令的传输.类似地,若路由中任意一跳的可用时间小于当前路由的重路由时间时,则当前的路径状态称之为危险链路状态,否则称之为正常链路状态,表示为
| $ \mathit{\boldsymbol{R}}\left( {{p_{ij}}} \right)\left\{ \begin{array}{l} 1,{\rm{危险链路状态}}\\ 0,{\rm{正常链路状态}} \end{array} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} \ \ \ \ \ \ \ \ ,i \ne j{\rm{且}}{p_{ij}}{\rm{存在}} $ | (9) |
提出的路由切换策略旨在卫星网络中保证数据传输不因路径切换而中断,基于轨道周期的链路预测结果决定是否启动路径切换过程,切换过程的处理分为链路预警和重路由2个阶段.
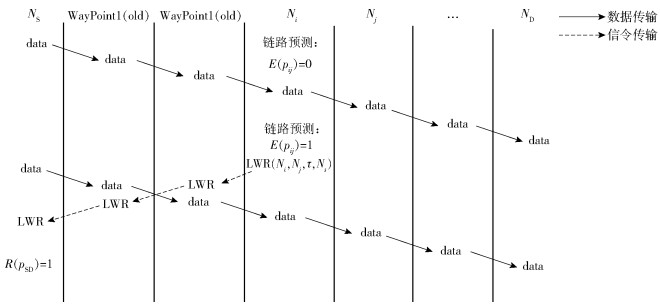
1) 链路预警过程:卫星节点在保证数据正常传输的同时进行链路预测,当满足2.1节中的路径切换条件时,则启动链路预警过程.当前节点给数据源节点发送链路预警报告(LWR, link warning report),LWR中包含即将断开的链路、断链时间以及路径的源节点地址.数据源节点收到LWR后,立即将该条路径设为危险状态.链路预警的完整过程如图 4所示,data代表传输数据,Waypoint1(old)代表旧路径的中间节点1,Waypoint2(old)代表旧路径的中间节点2.节点Ni判断出与Nj间的链路处于危险状态后,通过当前数据的反向路径发送预警消息LWR(Ni, Nj, τ, NS)至源节点NS,其中Ni和Nj为处于危险状态的链路所对应的节点,τ为链路预测算法计算的断链时间. NS接收到预警报告后,设置当前路径为危险状态,并主动开启重路由过程.
|
图 4 链路预警过程时序图 |
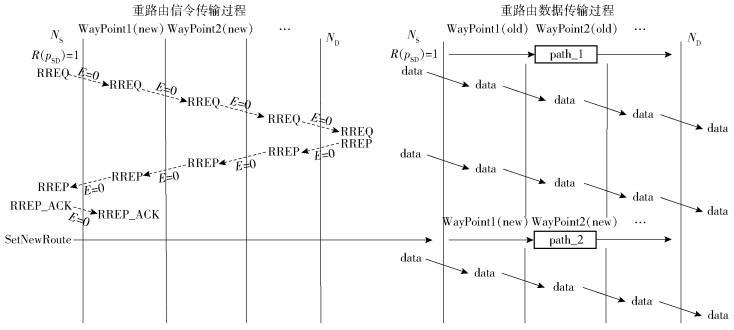
2) 重路由过程.路由重新发现过程中,任何链路状态为危险的链路都不能传输路由信令.重路由的同时,数据保持在原路径上持续传输.当重路由过程结束时,源节点找到新的可用路径后立即删除旧路径,同时数据传输也切换到新路径上进行.重路由的完整过程如图 5所示,WayPoint1(new)代表新路径的中间节点1,WayPoint2(new)代表新路径的中间节点2,RREQ(youte request)代表路由请求消息,RREP(route reply)代表路由回复消息,RREP_ACK代表RREP的回复消息.通过在安全状态的链路上转发路由寻路信息和路由回复信息建立新的可用路径,在源节点NS寻找新路径的同时,从NS到ND的旧路径Path_1仍然承载数据传输,但是当寻路过程完成后,数据传输的路径就变为了新路径Path_2.
|
图 5 重路由过程时序图 |
在低轨卫星网络中采用动态路由算法最大的优势在于:可以根据当前网络状态进行灵活的路由分配,从而实现网络负载均衡,降低网络拥塞的概率.为了突出这一优势,提出一种基于链路负载代价的最佳路径选择方式,定义了反映链路负载以及资源消耗的链路代价,从而寻找更有效的传输路径.首先,定义链路代价为
| $ {C_{{\rm{ISL}}}} = \left\{ {\begin{array}{*{20}{l}} {1,\quad {Q_1} \le {Q_{{\rm{th}}}}}\\ {{2^{{Q_1}/{Q_1} - 1}},\quad {Q_1} > {Q_{{\rm{th}}}}} \end{array}} \right. $ | (10) |
链路代价越大,使用该条链路进行传输消耗的资源就越多.其中,Ql为当前链路缓冲区长度,Qth为缓冲区阈值.当缓冲区长度小于阈值时,链路可以正常传输,不会造成拥塞,其代价设置为1;当缓冲区长度大于阈值时,采用指数函数描述其代价变化.对于整条路径来说,以链路代价之和定义路径代价,即
| $ {C_{{\rm{path}}}} = \sum\limits_{i = 1}^H {{C_{{\rm{ISL}}(i)}}} $ | (11) |
其中H为链路跳数.
其次,定义链路负载系数ρ表征网络中所有链路的平均带宽使用占比:
| $ \rho = \frac{{{S_{{\rm{ total }}}}{n_{{\rm{ hop }}}}}}{{{S_{{\rm{ ISL }}}}{n_{{\rm{ ISL }}}}}} $ | (12) |
其中:Stotal为全网接入业务的总速率,nhop为全网业务的平均跳数,SISL为星间链路速率,并且所有星间链路速率相同,nISL为网络总的链路数量.全网业务负载状态较高时,路径代价中跳数所占权重将增加,从而减小引入的网络负载,因此,路径代价函数定义为
| $ {C_{\rm{g}}} = {\left( {\frac{H}{{{H_{{\rm{min}}}}}}} \right)^{\frac{\rho }{\lambda }}}\sum\limits_{i = 1}^H {{C_{{\rm{ISL}}(i)}}} $ | (13) |
其中:λ为代价调节参数,根据不同网络特性进行调节.把函数的前半部分称为全局代价变量,后半部分称为路径代价变量.
当网络负载较低时,全局代价变量趋近于1,路径代价中缓冲区长度总是小于等于缓冲区阈值,则式(13)退化为
| $ {C_{\rm{g}}} = H $ | (14) |
在低负载情况下,路径选择变为一般的基于最小跳数原则的动态路由选择方案,且不考虑路径代价问题.
当网络负载较高时,全局代价变量和路径代价变量均会对结果产生较大影响,此时应按照式(13)选择综合代价最小路径.
当网络负载很高时,由于全局代价变量随业务负载系数指数增长,此时会对综合代价产生决定性的影响,在这种情况下,式(13)退化为
| $ {C_{\rm{g}}} = \sum\limits_{i = 1}^{{H_{{\rm{min}}}}} {{C_{{\rm{ISL}}(i)}}} $ | (15) |
即以最小跳数为原则,以路径代价为标准进行最优路径选择方式.
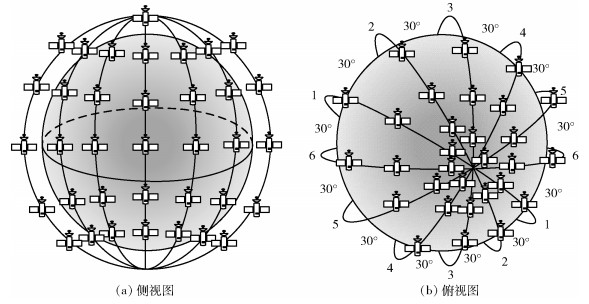
3 仿真及分析 3.1 性能分析仿真场景采用类铱星的极轨道星座,包含6条轨道,每条轨道10颗卫星,共60颗卫星.其中第1条轨道的节点编号设置为1~10,第2条轨道设置为11~20,依次类推.每1个卫星节点包含2条轨道内链路与2条轨道间链路,且与4个邻居节点相连,但是由于反向缝的存在,轨道1和轨道6之间不存在星间链路.最终的仿真场景如图 6所示.
|
图 6 仿真场景示意图 |
仿真参数设置如下:异轨最大星间距为3 701.63 km,同轨星间距为4 493.1 km,最大通信距离为4 846.7 km,运行周期为100 min,极区所占运行时间比例为20%,卫星运行速度为7.52 km/s.
ρ代表了网络负载情况,ρ越大,负载越重.依据多次不同场景下的实验结果,经验设置代价调节参数λ为1/160.星间链路速率设为2 Mbit/s,业务产生过程符合泊松分布,数据包大小设置为1 024 Byte,节点的缓冲区大小为500 MB,缓冲区阈值大小为100 MB,仿真时间为1个轨道运行周期.
仿真了3种路由机制并进行性能对比:基于预测的预先重路由并采用提出的综合代价路由度量,基于预测的预先重路由但采用最小跳数的路由度量,以及没有预先路由的最小跳数路由度量,统计丢包率和时延2项参数.目前主流的卫星网络使用的路由策略都是无预测的最小跳数度量,例如经典的快照路由、分布式路由算法等.需要说明的是,由于最小跳数原则和无预测的最小跳数原则在除了极区切换部分外完全一致,这2项仅在切换产生的丢包率上存在差异,而在时延上几乎相同,因此在时延统计中只包含综合代价度量和最小跳数度量2项.
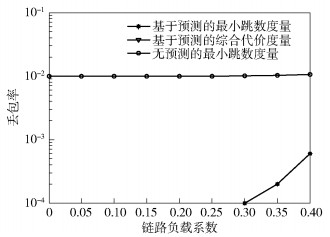
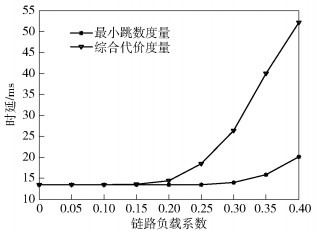
首先设置ρ=[0, 0.4],网络丢包率和时延如图 7和图 8所示.基于预测的综合代价度量方法所产生的丢包率全部为零,因此在图 7中没有显示.可以看出,负载较轻时,采用综合代价度量的路由策略和采用最小跳数度量的路由策略时,其丢包率和时延几乎相同,仅在链路负载系数ρ上升到一定程度后有比较小的差距,与式(14)相符合.在无预测的路由机制中,链路断开和路径重建的过程会造成一部分分组丢失.由于提出的主动重路由机制避免了路径断开被动的重路由过程,路径切换零损失,因此丢包率近似为0.
|
图 7 ρ=[0,0.4]情况下的丢包率 |
|
图 8 ρ=[0,0.4]情况下的单跳时延 |
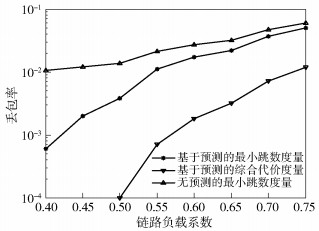
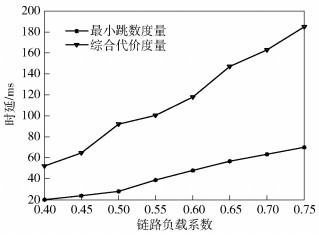
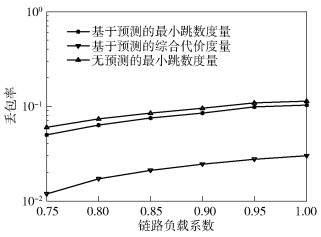
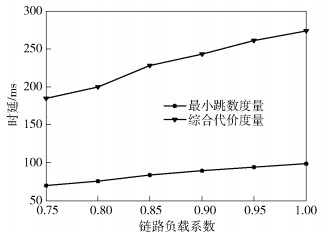
当ρ=[0.4, 0.75]时,网络丢包率和时延如图 9和图 10所示.随着链路负载系数的提升,采用最小跳数的路由度量时会出现各节点负载不均的情况,而本文提出的路由度量考虑了路径的综合代价,节点会选择代价相对较低的路径,使网络中所有的业务尽可能地均匀分布在不同节点上,充分提高网络的资源利用率.仿真结果表明,相比最小跳数的路由度量,提出的路由机制在丢包率和时延方面都有较为明显的性能提升.在ρ=[0.75, 1]情况下,网络丢包率和时延如图 11和图 12所示.可以看出,随着网络负载进一步加重,提出的度量相比传统最小跳数方法,性能增益更大.
|
图 9 ρ=[0.4,0.5]情况下的丢包率 |
|
图 10 ρ=[0.4, 0.75]情况下的单跳时延 |
|
图 11 ρ=[0.75,1]情况下的网络丢包率 |
|
图 12 ρ=[0.75,1]情况下的单跳时延 |
在低轨卫星网络中,每进行1次全网范围内的路径查询,会访问所有的星间链路1次,在卫星数量为n,且每个卫星具有4条(反向缝两侧为3条)星间链路的极轨道星座中,星间链路总数大约为2n,网络中路径最大跳数为m,路径切换信令的平均大小为Mavg,则每完成1次路径切换造成的信令开销为
| $ (2n + m){M_{{\rm{avg}}}} $ | (16) |
设1个周期内卫星网络产生的业务数为fnum,且每1个业务都会在1个周期内进行最多n/P次路径切换,则最坏情况下,在1个周期T内由于路径切换造成的开销为
| $ {f_{{\rm{ num }}}}\frac{n}{P}(2n + m){M_{{\rm{avg}}}} $ | (17) |
针对低轨卫星网络中的路径切换问题,提出了一种基于预测的路径切换机制.该方案以链路预测为基础,打破了传统网络中链路断链重连的模式,在路径完全中断之前完成重路由过程,并且根据网络负载情况设计综合代价函数,以卫星节点缓冲区数据量的大小和路径跳数作为主要评判标准,选择最优的数据传输路径,实现网络负载均衡,并进行了仿真实验,结果表明所提方法在时延和丢包率等性能方面均有明显提升.
| [1] |
Liu G P, Zhang S. A survey on formation control of small satellites[J]. Proceedings of the IEEE, 2018, 106(3): 440-457. DOI:10.1109/JPROC.2018.2794879 |
| [2] |
Radhakrishnan R, Edmonson W, Afghah F, et al. Survey of inter-satellite communication for small satellite systems:physical layer to network layer view[J]. IEEE Communications Surveys & Tutorials, 2017, 18(4): 2442-2473. DOI:10.1109/COMST.2016.2564990 |
| [3] |
秦勇, 惠蕾放, 刘晓旭, 等. 分布式空间系统星间通信组网技术研究综述[J]. 空间电子技术, 2015, 12(4): 1-10. Qin Yong, Hui Leifang, Liu Xiaoxun, et al. Survey:inter-satellite networking technologies of distributed space systems[J]. Space Electronic Technology, 2015, 12(4): 1-10. DOI:10.3969/j.issn.1674-7135.2015.04.001 |
| [4] |
晏坚.低轨卫星星座网络IP路由技术研究[D].北京: 清华大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280339.htm
|
| [5] |
Liu Y, Liu C. Distributed dynamic routing algorithm for satellite constellation[C]//2018 10th International Conference on Communication Software and Networks. New York: IEEE Press, 2018: 300-304. 10.1109/CONTROLO.2018.8439835
|
| [6] |
Liu Y, Zhu L. A suboptimal routing algorithm for massive LEO satellite networks[C]//2018 International Symposium on Networks, Computers and Communications. New York: IEEE Press, 2018: 1-5. 10.1109/ISNCC.2018.8530894
|
| [7] |
Yan D, Guo J, Wang L, et al. SADR: network status adaptive QoS dynamic routing for satellite networks[C]//2016 IEEE 13th International Conference on Signal Processing. New York: IEEE Press, 2016: 1186-1190. 10.1109/ICSP.2016.7878015
|
| [8] |
Meng W, Hong Z J, Xi L, et al. An inter satellite link handover management scheme based on link remaining time[C]//2016 2nd IEEE International Conference on Computer and Communications. New York: IEEE Press, 2016: 1799-1800. 10.1109/CompComm.2016.7925012
|
| [9] |
Werner M, Delucchi C, Vogel H J, et al. ATM-based routing in LEO/MEO satellite networks with intersatellite links[J]. IEEE Journal on Selected Areas in Communications, 2002, 15(1): 69-82. |
| [10] |
Uzunalioglu H. Probabilistic routing protocol for low earth orbit satellite networks[C]//1998 IEEE International Conference on Communications. New York: IEEE Press, 1998: 89-93. 10.1109/ICC.1998.682592
|
| [11] |
曹志刚, 王京林, 晏坚. LEO卫星网络快照序列路由算法优化[J]. 宇航学报, 2009, 30(5): 2003-2007. Cao Zhigang, Wang Jinglin, Yan Jian. Optimization of sequent snapshots routing algorithm in LEO satellite networks[J]. Journal of Astronautics, 2009, 30(5): 2003-2007. DOI:10.3873/j.issn.1000-1328.2009.05.043 |
| [12] |
Li J, Lu H, Wang Y. Temporal netgrid model based routing optimization in satellite networks[C]//2017 IEEE International Conference on Communications. New York: IEEE Press, 2017: 1-6. 10.1109/ICC.2017.7996551
|
| [13] |
Yarr N, Ceriotti M. Optimization of inter-satellite routing for real-time data download[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2356-2369. DOI:10.1109/TAES.2018.2815880 |
| [14] |
Yang L, Sun J. Multi-service routing algorithm based on GEO/LEO satellite networks[C]//2016 International Conference on Network and Information Systems for Computers. New York: IEEE Press, 2016: 80-84. 10.1109/ICNISC.2016.027
|


