在大规模多输入多输出(MIMO, multiple input multiple output)系统中，多用户(MU, multi-user)技术因可大幅提升系统的频谱效率(SE, spectral efficiency)而被广泛采用^[1].为保证MU的良好性能，基站需获得较准确的信道状态信息(CSI, channel state information).时分双工(TDD, time duplex division)因可利用上下行信道的互易性而备受推荐^[2]. TDD系统中基站利用探测参考信号(SRS, sounding reference signal)估计上行CSI来近似代替下行CSI，TDD很好地保障了MU的良好性能.

实际中SRS资源十分有限，SRS受限的原因包括^[3]：1)为避免多小区间导频污染，基站不会使用全部SRS序列；2)为满足用户更高的速率需求，MU数需进一步增多，此时需要更多的CSI来近似下行信道；3)移速快的用户因多普勒分量增大而引起信道过时加重. SRS资源受限时，基站每次只能更新部分用户的下行信道.如果只调度CSI准确的用户，不仅MU数受限，而且用户间的信道相关性会造成能量损失；然而若将所有用户都纳入可调度集合，过时CSI却会引入干扰. SRS资源受限造成的系统SE恶化已成为重要问题.

相关学者已给出一些缓解SRS受限的方案. CSI参考信号(CSI-RS，CSI reference signal)用来测量过时CSI，通过给出准确用户与非准确用户的标准和多用户分组调度可以实现吞吐量和公平性的提升^[3].此外还有作者提出基于聚类的分组调度方法来缓解CSI有限造成的能量损耗^[4].但文献[3]中方法测量效果有限，而文献[4]中方法复杂度过高且性能不稳定.缓解SRS受限的算法仍有改善空间.

为改善SRS受限造成的系统SE恶化问题，笔者提出联合导频分配的用户分组调度方案.为使基站获得更多较准确的CSI，优化导频分配的效率更高.由于实际中用户移速、视距传播情况等原因，不同用户CSI变化的速率不同，因此可为设置不同的用户探测周期.首先研究了用户CSI变化的特性，给出确定用户探测周期的算法，根据用户的探测周期，提出导频分配方案；最后基于SoCC(square of channel correlation)准则^[5]，提出多用户分组调度方案，并利用3-D MIMO信道验证了所提算法的可有效提升系统的性能.

1 系统模型 1.1 3-D MIMO信道模型

假设有二维的矩形阵列，t时刻的时域径为^[3]

$ \begin{array}{*{20}{c}} {{h_{u,s,n}}(t) = }\\ {\sum\limits_{m = 1}^M {(\sqrt {{P_{n,m}}} \{ } {c_{u,s,n,m}}{\rm{exp}}({\rm{j}}2\pi {\lambda ^{ - 1}}{\mathit{\boldsymbol{d}}_s}{\mathit{\boldsymbol{\varphi }}_{n,m}}) \times }\\ {{\rm{exp}}({\rm{j}}2\pi {\mathit{\boldsymbol{d}}_u}\mathit{\boldsymbol{\varphi }}_{n,m}^\prime ) \times {\rm{exp}}({\rm{j}}2\pi {v_{n,m}}t)\} )} \end{array} $

(1)

其中：u、s分别为基站和用户天线编号，P_{n, m}为时域径m中子径n的能量，c_{u, s, n, m}为由方向图和初始随机相位计算得到的参数，d_s和d_u代表位置，φ_{n, m}和φ′_{n, m}为离开和到达角，v_{n, m}为多普勒分量.根据文献[6]中的计算方法，可得用户在基站天线的时域信道，再进行FFT便可得用户的频域信道.

1.2 SRS容量

假设小区内扇区的数目为N_S，每个扇区占用相同的SRS资源，则一个扇区的SRS容量为^[3]

$ {N_{{\rm{ SecSRS }}}} = \frac{{{B_{{\rm{BS}}}}{N_{{\rm{CS}}}}{N_{\rm{C}}}{T_{{\rm{UE}}}}}}{{{B_{{\rm{UE}}}}{T_{{\rm{BS}}}}{N_{\rm{S}}}}} $

(2)

其中：B_BS和B_UE分别代表基站和用户的SRS带宽，N_CS为循环移位数，N_C为序列数，N_S代表梳状结构，T_BS为基站探测周期，T_UE为用户探测周期，基站探测用户数$N_{\rm SecSRS}^{\rm Per}$可假设T_UE=T_BS计算得出.

1.3 SINR与SE

以单小区为研究场景，基站和用户天线数分别为N_T和1，总用户数为K₀，MU数为K.接收信号y∈C^K×1为

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\eta H}}{\mathit{\boldsymbol{\hat W}}^{{\rm{norm}}}}{\mathit{\boldsymbol{P}}^{1/2}}\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{n}} $

(3)

其中：η和P为对角阵，分别为大尺度衰落和发射功率；H∈C^K×N_T为实际信道；x∈C^K×1为数据，n∈C^K×1为高斯白噪声，${{\mathit{\boldsymbol{\hat W}}}^{\rm norm}} \in {C^{{N_{\rm T}} \times K}}$为归一化的估计预编码矩阵，计算方法为

$ {\mathit{\boldsymbol{\hat W}}^{{\rm{ norm }}}} = \left[ {\frac{{{{\mathit{\boldsymbol{\hat w}}}_1}}}{{\left\| {{{\mathit{\boldsymbol{\hat w}}}_1}} \right\|}},\frac{{{{\mathit{\boldsymbol{\hat w}}}_2}}}{{\left\| {{{\mathit{\boldsymbol{\hat w}}}_2}} \right\|}}, \cdots ,\frac{{{{\mathit{\boldsymbol{\hat w}}}_K}}}{{\left\| {{{\mathit{\boldsymbol{\hat w}}}_K}} \right\|}}} \right] $

(4)

其中：${{\mathit{\boldsymbol{\hat w}}}_i}$为估计迫零预编码矩阵${\mathit{\boldsymbol{\hat W}}}$的第i列，且有

$ \mathit{\boldsymbol{\hat W}} = {\mathit{\boldsymbol{\hat H}}^{\rm{H}}}{(\mathit{\boldsymbol{\hat H}}{\mathit{\boldsymbol{\hat H}}^{\rm{H}}})^{ - 1}} $

(5)

${\mathit{\boldsymbol{\hat H}}}$∈C^K×N_T为估计信道，则信号干扰加信噪比(SINR，signal to interference plus noise ratio)γ_k为

$ {\gamma _k} = \frac{{{p_k}{\eta _k}|{\mathit{\boldsymbol{h}}_k}{{\mathit{\boldsymbol{\hat w}}}_k}{|^2}}}{{{{\left\| {{{\mathit{\boldsymbol{\hat w}}}_k}} \right\|}^2}\sum\limits_{j = 1,j \ne k}^K {({\eta _k}|{\mathit{\boldsymbol{h}}_k}{{\mathit{\boldsymbol{\hat w}}}_j}{|^2}/{{\left\| {{{\mathit{\boldsymbol{\hat w}}}_j}} \right\|}^2})} + {B_k}\sigma _{\rm{n}}^2}} $

(6)

其中：p_k为基站对用户k的发射功率，设每个用户功率相同，则有p_k=P_t/K，P_t为总体发射功率；η_k为用户k的大尺度衰落；$\sigma _{\rm n}^2$为噪声功率谱密度；B_k为传输带宽.定义用户k和j间的信道相关性为

$ {\rho _{kj}} = \frac{{|{\mathit{\boldsymbol{h}}_k}\mathit{\boldsymbol{h}}_j^{\rm{H}}|}}{{\left\| {{\mathit{\boldsymbol{h}}_k}} \right\|{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\| {{\mathit{\boldsymbol{h}}_j}} \right\|}} $

(7)

根据香农定理，系统SEω为

$ \omega = \sum\limits_{k = 1}^K {\rm{l}} {\rm{b}}(1 + {\gamma _k}) $

(8)

2 联合导频分配的多用户分组调度 2.1 问题描述与总体思路

已有的多用户分组调度研究中通常假设已知全部用户的CSI.在SRS受限即$N_{\rm SecSRS}^{\rm Per}$有限场景中，基站每次只能更新部分用户CSI，而未被探测的用户的CSI失准.如果调度CSI严重过时的用户，过时用户性能严重恶化；然而，如果只调度基站刚探测的用户，不仅MU数目受限，而且很多功率会被损耗以抵消信道相关性.由于候选用户集合受导频分配影响，多用户分组调度需联合导频分配，扩充可调度集合，才能合理高效调度用户.

提出的联合导频分配多用户分组调度算法包括3部分：用户信道探测周期的测量；基于信道变化速率的导频分配；基于信道变化速率的多用户分组调度.

图 1为提出算法的总体流程，其中：L为轮询探测K₀个用户所需的基站探测周期数，I为导频分配与分组调度的时长，仿真时长T_tot为I+2L.下面具体阐述联合导频分配的多用户分组调度算法的3部分算法.

2.2 用户信道探测周期的测量

假设用户k在t时刻的实际信道为h_k(t), 间隔时间T后的信道为h_k(t+T)，目标信道相关性门限为α，则用户探测周期测量准则可以描述为

${T_{{\rm{UE}}}^k = \tilde T_{{\rm{UE}}}^k{T_{{\rm{BS}}}}} $

(9)

且

$ {\tilde T_{{\rm{UE}}}^k = \left\lfloor {{\rm{argmax}}{\tau _k}} \right\rfloor } $

(10a)

$ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha - \rho ({\tau _k}) > 0} $

(10b)

其中：${\rho _t}({\tau _k}) = \frac{{\left| {{\mathit{\boldsymbol{h}}_k}(t)\mathit{\boldsymbol{h}}_k^{\rm H}(t + {\tau _k}{T_{\rm BS}})} \right|}}{{\left\| {{\mathit{\boldsymbol{h}}_k}(t)} \right\|\left\| {{\mathit{\boldsymbol{h}}_k}(t + {\tau _k}{T_{\rm BS}})} \right\|}}$为以时间t为基准，用户经时间τ_kT_BS后的CSI与t时刻CSI的相关性，ρ_t(τ_k)越大说明CSI变化越小；α为设定的最低阈值，其物理意义为最低信道准确度.

对时间t，由ρ_t(0)=1定义信道变化速率为

$ {v_t}({\tau _k}) = \frac{1}{{{\tau _k}{T_{{\rm{BS}}}}}}(1 - {\rho _t}({\tau _k})) $

(11)

由于T_BS很短，若干T_BS内时域径的到达离开角，移动性及视距情况等可近似不变，短时间内v(τ_k)几乎不随测量时刻变化，即t与$\widetilde t$很接近时v_t(τ_k)≈v_{$\widetilde t$}(τ_k).基于此即可估算t+ΔT时刻与t时刻的真实信道相关性，方法为

$ {\rho _t}\left( {\frac{{\Delta T}}{{{T_{{\rm{BS}}}}}}} \right) \approx 1 - {v_t}(1)\frac{{\Delta T}}{{{T_{{\rm{BS}}}}}} $

(12)

因此v_t(1)和式(12)可被当成确定$T_{\rm UE}^k$的重要依据.此时，用户信道探测周期测量标准转化为

$ T_{{\rm{UE}}}^k = f(\alpha ,{v_t}(1)) $

(13)

综上所述，通过仿真统计所有满足v_t(1)≤1－α的用户随时间的相关性变化趋势，即可得$T_{\rm UE}^k$=f(·)，仿真结果见3.2节.用户信道探测周期的测量算法如下(此算法的执行周期为若干T_BS).

算法1 用户信道探测周期测量

输入：$N_{\rm SecSRS}^{\rm Per}$，K₀

输出：用户信道探测周期$T_{\rm UE}^k$，且k=1, 2, …, K₀

1 对于轮次i=1:2L

2 计算被探测用户的起始与终止编号为：${K_{\rm s}} = \left\lceil {i/2} \right\rceil N_{{\rm{SecSRS}}}^{{\rm{Per}}} + 1,{K_{\rm e}} = \left( {\left\lceil {i/2} \right\rceil + 1} \right)N_{{\rm{SecSRS}}}^{{\rm{Per}}}$；

3 对于用户k=K_s:K_e

4 探测估计用户k在轮次i的信道h_k(i)；

5 如果mod(i, 2)等于0；

6 用h_k(i)，h_k(i－1)计算用户k的v(1)和$T_{\rm UE}^k$(见式(17))；

2.3 基于信道变化速率的导频分配

假设轮次i的子帧时间s_i，调节因子T_c，用户k的传输速率r_k(s_i)=B_klb(1+γ_k)，则平均速率为

$ {R_k}({s_i}) = (1 - 1/{T_c}){R_k}({s_i} - 1) + {r_k}({s_i})/{T_{\rm{c}}} $

(14)

信道变化慢的用户应有高优先级，因为他们在若干T_BS内都可被调度，成为“扩充用户”.基于PF算法，提出优先级的计算方法为

$ \xi _k^{{\rm{esti}}}({s_i}) = \frac{{\gamma _k^{{\rm{CQI}}}({s_i})}}{{{R_k}({s_i})}} \cdot {10^{T_{{\rm{UE}}}^k}} $

(15)

其中：$\gamma _k^{{\rm{CQI}}}$代表用户的信道质量指示(CQI，channel quality indicator)，为线性数值.基于信道变化速率的导频分配算法如下.

算法2 基于信道变化速率的导频分配

输入：$N_{\rm SecSRS}^{\rm Per}$，K₀，K，$T_{\rm UE}^k$，B_k，R_k(s_i)，最临近被探测时间i_k，其中k=1, 2, …, K₀

输出：不同基站探测轮次i的探测集合$\mathscr{G}$

1 对于用户k=1:K₀

2 如果i－i_k>$T_{\rm UE}^k$

3 将用户k加入待探测集合$\mathscr{G}$；

4 利用式(15)计算待探测集合$\mathscr{G}$中用户优先级；

5 将$\mathscr{G}$中用户按照优先级$\xi _k^{{\rm{esti}}}$由大到小排序；

6 选择前$N_{\rm SecSRS}^{\rm Per}$用户组成轮次i的探测集合$\mathscr{G}$；

7 更新$\mathscr{G}$中用户的信道探测轮次为i

2.4 基于信道变化速率的多用户分组调度

SoCC标准可使CSI相关性造成的能量损耗接近最低^[5].本分组调度方案基于SoCC，分为3个步骤：

1) 筛选得到预选调度集合；

2) 从本轮探测的准确用户集合中选择优先级最大的用户加入调度集合，优先级计算方法为

$ \xi _k^{{\rm{ sche }}}({s_i}) = \frac{{\gamma _k^{{\rm{ CQI }}}({s_i})}}{{{R_k}({s_i})}} $

(16)

3) 从预选调度集合选择与调度集合用户的SoCC之和最小的用户加入调度集合，持续此操作直到达到预设调度多用户数.

提出的基于信道变化速率的多用户分组调度算法如下.

算法3 基于信道变化速率的多用户分组调度

输入：K₀，$T_{\rm UE}^k$，B_k，最临近时刻s_c的平均速率R_k(s_c)，最邻近探测时间i_k，其中k=1, 2, …, K₀

输出：多用户分组调度集合$\mathscr{G}$

1 对于用户k=1:K₀

2 将i－i_k < $T_{\rm UE}^k$的用户加入预选调度集合$\mathscr{U}$；

3 将i－i_k < $T_{\rm UE}^k$的用户加入预选调度集合$\mathscr{V}$；

4 利用式(17)计算用户k∈$\mathscr{V}$的优先级；

5 选择优先级最大的用户k_max加入调度集合$\mathscr{Q}$；

6 如果调度集合$\mathscr{Q}$中用户数小于K，循环

7 对于用户k∈$\mathscr{U}$

8 利用式(7)计算用户k与所有j∈$\mathscr{Q}$的相关性，并求和得相关性之和为$C_k^{{\rm{sum}}}$；

9 选择使$C_k^{{\rm{sum}}}$最小的用户k_min加入$\mathscr{Q}$，并从$\mathscr{U}$中删除用户k_min

3 仿真结果 3.1 仿真配置

表 1所示为仿真的主要配置^[7-9].由于市区内的2种常见移速场景为3 km/h和30 km/h，而且实际环境中同时存在多种移速，所以配置用户的移动速度均匀分布在[3 km/h, 30 km/h]区间.假设上行信道估计是理想的，这表明基站通过信道估计得到的CSI只包含过时误差，而不包含估计误差.

3.2 信道变化趋势与目标相关性门限

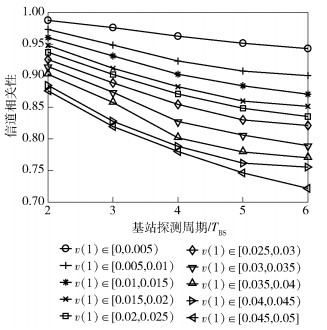
配置α的数值为0.95.如图 2所示，用户在时域信道的信道相关性随时间间隔增大而减小. 图 2的绘制方法为：计算所有满足v(1) < 0.05的用户在若干T_BS间隔的相关性，即统计了10种用户在5种不同的T_BS间隔的相关性，则可得到总计50种组合的相关性数值集合.对于每一种组合的相关性数值从小到大排序，取第10%小的相关性作为这种组合的数值.根据图 2和α即可确定$T_{\rm UE}^k$.如若k的v(1) < 0.005，从图 2由ρ(5) < 0.95 < ρ(4)可得$T_{\rm UE}^k$=4.以此方法可以得到式(17).

$ f(\alpha = 0.95,v(1)) = \left\{ {\begin{array}{*{20}{l}} {4,}&{v(1) \in [0,0.005)}\\ {3,}&{v(1) \in [0.005,0.015)}\\ {2,}&{v(1) \in [0.015,0.05)}\\ {1,}&{v(1) \in [0.05,1]} \end{array}} \right. $

(17)

结合式(13)和式(17)可得用户k的$T_{\rm UE}^k$=f(α=0.95, v(1)).

3.3 系统性能分析

为方便表述，将所提的方案简称为联合用户分组的导频分配(PAUG, pilot allocation with user grouping)方案.下面给出PAUG方案与文献[1]中基于CSI-RS的联合分组调度方案(CJGSS, CSI-RS based joint grouping and scheduling scheme)和自适应用户分组方案(AUGS, adaptive user grouping scheme)在SINR、用户SE、系统SE三个性能指标上的对比.

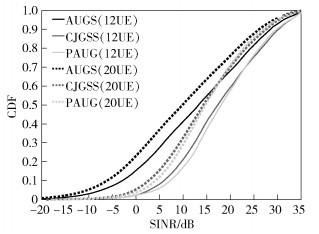
CJGSS方案利用CSI-RS测量过时CSI，选择符合要求的过时用户，并同准确用户一起调度；AUGS为常见方案，即轮询探测只基于相关性调度用户. 图 3给出3种方案的SINR的累积分布函数(CDF，cumulative distribution function)曲线. SRS受限时AUGS性能极差，当多用户数为20，超过20%的SINR低于0，可见提出缓解SRS资源受限算法的必要性. CJGSS和PAUG都提升了SINR. PAUG对用户数较多时的低SINR区域性能提升更明显，因为PAUG方法可更好地扩充调度集合.然而多用户数较少时，PAUG仍实现了SINR的提升.

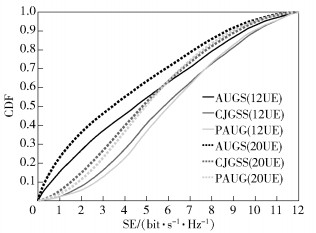
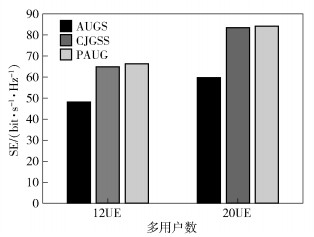
图 4给出了用户SE的性能对比，因为CJGSS的测量效果有限，对相关性造成能量损耗的抑制效果不好，所以CJGSS的用户SE一直弱于PAUG方案. 图 5给出了系统SE的性能对比.在系统SE性能上，PAUG方案相比于AUGS方案在多用户数为12和20时分别提升了37.9%和40.9%；而相比于CJGSS，PAUG方案也略有提升，但需注意CJGSS会造成下行导频开销. 图 5证实了PAUG方案的适用性.

3.4 时间复杂度分析

假设待探测用户数K′=|$\widetilde G$|，PAUG方案所包含的3部分算法的时间复杂度分别为O(K₀N_T)、O(K₀+K′N_T+K′log₂K′)、O((K₀－K′+$N_{\rm SecSRS}^{\rm Per}$)²N_T)；AUGS中，用户不被区分，因此AUGS只包含调度算法的时间复杂度，且为O($K_0^2$N_T)；CJGSS共包含2部分的时间复杂度，分别为O((K₀－$N_{\rm SecSRS}^{\rm Per}$)(N_T+lb(K₀－$N_{\rm SecSRS}^{\rm Per}$)))和O(($N_{\rm SecSRS}^{\rm Per}$+K_CJGSS)²N_T)，其中的K_CJGSS为可调度用户数. PAUG方案的复杂度小于AUGS，虽然略高于CJGSS，但是系统性能得到了提升.

4 结束语

TDD大规模天线系统中，SRS资源受限，导致下行CSI过时，进而使SE性能恶化.为此，提出了联合导频分配的多用户分组方案，方案包括用户信道探测周期测量；基于用户信道变化速率的导频分配与多用户分组调度算法.仿真结果表明, 相比于普遍假设的非SRS受限方案，所提方案可使系统的SE性能显著提升，且提升幅度高达40%，性能更优.