2. 北京邮电大学 电子工程学院, 北京 100876
为了解决全双工能量受限中继网络的无线物理层安全问题,提出了一种基于能量和信息联合传输的安全波束成形方法.在满足中继节点和能量收集节点收集能量的约束条件下,通过联合优化能量信号协方差矩阵、波束成形矩阵和功率分配因子,实现了系统安全速率最大化.目标问题是非凸的,采用分步优化方法将原始问题转化为2个子问题.将第1个子问题转化为双层优化问题,外层优化问题采用一维搜索求解,内层优化问题采用半定松弛技术解决;然后通过一维搜索得到第2个子问题的最优解.仿真结果表明,提出的方法显著提高了系统的安全速率.
2. School of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China
In order to solve the problem of optimizing the security rate of full duplex relay eavesdropping channel with energy harvesting capability, a secure beamforming design was proposed under simultaneous wireless information and power transfer (SWIPT) method. An optimization problem was considered aiming to maximize the secrecy rate of the system by jointly optimizing the beamforming matrix, energy signal covariance matrix and the power splitting ration under the constraint of the energy harvesting of the relay and energy-harvesting node. Since this problem is a non-convex secrecy rate maximization (SRM) problem, We use a step-by-step optimization approach to turn the objective problem into two sub-problems was decoupled. The first subproblem can be recast as a two-level optimization problem. Among them, the outer optimization problem was solved by one-dimensional search, and the inner optimization problem was solved by semidefinite relaxation (SDR) technique. The second subproblem can be solved by one-dimensional search. Simulation results show that the proposed method increases the security rate of the system.
引由于无线通信的广播特性和开放特性,导致信息很容易被窃听者窃取,使无线网络的安全问题亟待解决[1].近年来,无线物理层安全技术得到了诸多学者的研究.中继节点不仅能够有效扩大网络传输范围,提高空间多样性,从而能够提升无线网络中物理层的安全性[2].随着自干扰(SI,self-interference)消除技术的发展,使得中继采用全双工工作方式成为可能.全双工中继能够实现同时收发信息,提高了信息传输效率,满足了5G网络对用户数据业务高速增长的需求[3].中继协作加干扰技术有效提高了物理层安全性. Li等[4]对放大转发(AF,amplify and forward)多中继网络提出一种具有鲁棒性的合作波束成形和人工噪声联合优化的方法,在同时存在多个窃听者的情况下该方法极大提高了系统的安全性. Sun等[5]研究了具有一个全双工基站和多个半双工移动用户的安全传输系统,下行链路产生人工噪声.通过对下行波束形成器、人工噪声协方差矩阵和上行发射功率的联合优化以提高系统的安全性能.张等[6]在放大转发中继系统中,为了解决信息很容易被窃听者窃取的问题,提出了在中继节点处转发信息时发送人工噪声的安全波束成形方法.但上述文献没有考虑能量收集问题,限制了无线网络的寿命.
未来5G网络的大规模使用将带来用户数据业务的快速增长,从而严重制约能量受限网络的寿命[7].近年来,一种从射频(RF,radio frequency)信号中捕获能量的技术引起了研究者浓厚的兴趣. RF信号能同时传递信息和能量,由此产生了信息和能量联合传输(SWIPT,simultaneous wireless information and power transfer)[8]. Özlem等[9]在全双工解码转发(DF,decode- and-forward)无线供电的中继系统中,中继应用功率分裂技术将信息和能量同时存储到多天线中继系统中. Xing等[10]在能量收集系统中,联合优化功率分配因子和能量转移策略来最大化系统安全速率(SRM,secrecy rate maximization). Zhao等[11]在无线供电的非再生多中继系统中优化安全波束成形,其中多天线中继可以从射频信号中收集能量. Feng等[12]在信息和能量联合传输的AF中继网络中设计了安全波束成形,以提高系统的安全性能,但是中继节点没有收集能量.
笔者研究的是能量受限全双工中继网络中, 存在多个窃听节点情况下的安全速率优化问题.为了保证能量受限全双工中继网络传输保密信息的安全性,多天线中继在放大转发信息时发射能量信号(ES, energy signal)对窃听节点进行干扰. ES与AN相似,但不同于AN,它是一种预先设计好的伪随机信号,在干扰窃听节点的时候不会对目的节点造成干扰,同时还能满足能量接收节点的能量需求.在满足中继和能量收集节点收集能量的约束条件下,通过联合优化能量信号协方差矩阵、波束成形矩阵和功率分配因子,使系统安全速率最大.仿真结果验证了所提出方法的有效性.
1 系统模型及问题描述 1.1 系统模型全双工能量受限的中继系统如图 1所示,由源节点A、中继节点R、信息接收节点B、能量收集节点C和K个窃听节点Ek组成.全双工中继采用放大转发工作方式,除中继节点配备M根接收天线和N根发射天线外,其他节点均配备单天线.假设在源节点和目的节点之间不存在直接链路,目的节点和窃听节点想要收到源节点发送的保密信息必须经过中继节点辅助转发信息.中继节点除了从RF信号中收集能量外再无其他能量供应源.在中继节点中安装功率分流器,ρ∈(0, 1)表示接收信号功率比例,将接收到的信号存储在信号接收器IR,information receiver中;剩余的(1-ρ)表示收集能量的功率比例,将收集到的能量存储在能量收集器ER,energy receiver中.定义f∈CM,h∈CN,g∈CN,tk∈CN分别为A~R、R~B、R~C、R~Ek的信道向量.另外,HRR∈CM×N表示从发射天线到接收天线产生的自干扰信道.

|
图 1 全双工能量受限中继网络 |
基于以上的假设,在第n个时隙,中继节点接收信号表示为
| $ {\mathit{\boldsymbol{y}}_R}[n] = \mathit{\boldsymbol{f}}{x_A}[n] + {\mathit{\boldsymbol{H}}_{{\rm{RR}}}}{\mathit{\boldsymbol{x}}_R}[n] + {\mathit{\boldsymbol{n}}_R}[n] $ | (1) |
其中:xA[n]为源节点A发送的保密信息,E(|xA[n]2)=PA,E(·)表示数学期望;nR[n]∈~CN(0, IM)为中继节点处引入的加性高斯白噪声,IM为M阶单位矩阵.采用PS策略将接收到的信号yR[n]分成两部分:一部分用来信息传输存入IR中;另一部分用来收集能量存入ER中,分别表示为
| $ {\mathit{\boldsymbol{y}}_R^{{\rm{IR}}}[n] = \sqrt \rho {\mathit{\boldsymbol{y}}_R}[n]} $ | (2) |
| $ {\mathit{\boldsymbol{y}}_R^{{\rm{ER}}}[n] = \sqrt {1 - \rho } {\mathit{\boldsymbol{y}}_R}[n]} $ | (3) |
中继节点将接收到的信号乘以一个波束成形矩阵,与此同时,中继节点发射能量信号ES用于干扰窃听节点,同时也起到给能量接收节点传输能量的作用.因此,中继节点的发送信号可以表示为
| $ {\mathit{\boldsymbol{x}}_R}[n] = \sqrt \rho \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{y}}_R}[n - \delta ] + \mathit{\boldsymbol{z}}[n] $ | (4) |
其中:z[n]~CN(0, Σ)为能量信号向量,Σ
为了使系统模型更加简单,在中继节点处采用破零约束,用W消除中继的自干扰.即
| $ \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}_{{\rm{RR}}}}\mathit{\boldsymbol{W}} = {\bf{0}} $ | (5) |
消除了自干扰后,中继节点R的发送信号可以表示为
| $ {\mathit{\boldsymbol{x}}_R}[n] = \sqrt \rho \mathit{\boldsymbol{W}}(\mathit{\boldsymbol{f}}{x_A}[n - \delta ] + {\mathit{\boldsymbol{n}}_R}[n - \delta ]) + \mathit{\boldsymbol{z}}[n] $ | (6) |
根据文献[13]中继节点的发射功率为PR=Tr(E(|xR[n]|2)),即
| $ {P_R} = \rho ({P_A}\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}} + \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}) + {\rm{Tr }}(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) $ | (7) |
其中Tr(·)表示矩阵的迹.忽略噪声后中继节点收集到的能量表示为
| $ {E_R} = \eta T(1 - \rho )({P_A}\left\| {{\kern 1pt} \mathit{\boldsymbol{f}}{\kern 1pt} } \right\|_2^2 + {P_R}\left\| {{\kern 1pt} {\mathit{\boldsymbol{H}}_{{\rm{RR}}}}{\kern 1pt} } \right\|_{\rm{F}}^{\rm{2}}) $ | (8) |
其中:η∈(0, 1]为能量转换效率,║·║F是矩阵的Frobenius范数.将公式(7)代入公式(8)中得到
| $ \begin{array}{*{20}{c}} {{E_R} = \eta T(1 - \rho )({P_A}\left\| \mathit{\boldsymbol{f}} \right\|_2^2 + }\\ {\left\| {{\mathit{\boldsymbol{H}}_{{\rm{RR}}}}} \right\|_{\rm{F}}^{\rm{2}}(\rho ({P_A}\left\| {\mathit{\boldsymbol{Wf}}} \right\|_2^2 + \left\| \mathit{\boldsymbol{W}} \right\|_{\rm{F}}^{\rm{2}}) + {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }})))} \end{array} $ | (9) |
因此,目的节点B、C和窃听节点Eκ接收到的信号可以分别表示为
| $ \begin{array}{l} {y_B}[n] = \sqrt \rho {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{W}}(\mathit{\boldsymbol{f}}{x_A}[n - \delta ] + \\ {\mathit{\boldsymbol{n}}_R}[n - \delta ]) + {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{z}}[n] + {n_B}[n] \end{array} $ | (10) |
| $ \begin{array}{l} {y_C}[n] = \sqrt \rho {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{W}}(\mathit{\boldsymbol{f}}{x_A}[n - \delta ] + \\ {\mathit{\boldsymbol{n}}_R}[n - \delta ]) + {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{z}}[n] + {n_C}[n] \end{array} $ | (11) |
| $ \begin{array}{l} {y_{E,k}}[n] = \sqrt \rho \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{W}}(\mathit{\boldsymbol{f}}{x_A}[n - \delta ] + \\ {\mathit{\boldsymbol{n}}_R}[n - \delta ]) + {\mathit{\boldsymbol{t}}^{\rm{H}}}\mathit{\boldsymbol{z}}[n] + {n_{E,k}}[n] \end{array} $ | (12) |
其中:nB[n]~CN(0, 1),nC[n]~CN(0, 1)和nE, k[n]~CN(0, 1)分别表示在目的节点B、C和窃听节点Ek处引入的加性高斯白噪声.目的节点B可以消除掉预先设计好伪随机信号Σ,根据上述公式可知,目的节点B和窃听节点Ek处的信干噪比以及目的节点C处收集到的能量分别为
| $ {\gamma _B} = \frac{{\rho {P_A}{\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}\mathit{\boldsymbol{h}}}}{{1 + \rho {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}\mathit{\boldsymbol{h}}}} $ | (13) |
| $ {\gamma _{E,k}} = \frac{{\rho {P_A}\mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}{\mathit{\boldsymbol{t}}_\mathit{\boldsymbol{k}}}}}{{1 + \rho \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}{\mathit{\boldsymbol{t}}_k} + \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{t}}_k}}} $ | (14) |
| $ {E_C} = \eta T(\rho {P_A}|{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{Wf}}{|^2} + \rho {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}\mathit{\boldsymbol{g}} + {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} g}}) $ | (15) |
系统可达的安全速率表示为
| $ {R_S} = \mathop {{\rm{min}}}\limits_{k \in K} \{ {\rm{log}}(1 + {\gamma _B}) - {\rm{log}}(1 + {\gamma _{E,k}})\} $ | (16) |
研究的的目标是在中继节点R发射功率和能量收集节点C收集能量的共同限制下,通过联合优化能量信号协方差矩阵、波束成形矩阵和功率分配因子,使系统的安全速率最大.该问题可以表示为
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R_s^* = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{W}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \succeq 0,\rho } \mathop {{\rm{min}}}\limits_{k \in K} \{ {\rm{log}}(1 + {\gamma _B}) - {\rm{log}}(1 + {\gamma _{E,k}})\} }\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {P_R} \le {P_{{\rm{max}}}},{P_R} \ge {P_{R,{\rm{min}}}},{P_C} \ge {P_{C,{\rm{min}}}},0 < \rho < 1} \end{array} $ | (17) |
其中:Pmax=ER/T为中继节点的最大传输功率;PR, min>0为中继节点所需的最低传输功率;PC=EC/T;PC, min≥0为能量收集节点C所需功率.
2 安全波束形成方法式(17)为非凸的优化问题,无法对其直接求解于是可以采用分步优化方法将其转化为2个子问题进行求解[6].首先固定ρ的值,联合优化波束成形向量W和能量信号协方差矩阵Σ.其次,再根据得到的W和Σ优化功率分配因子ρ.
2.1 联合优化W和Σ固定功率分配因子ρ,引入松弛变量τ,将式(13)~(15)代入式(17)中得到
| $ \begin{array}{l} R_s^* = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{W}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \succeq 0} {\rm{log}}\left( {1 + \frac{{\rho {P_A}{\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}\mathit{\boldsymbol{h}}}}{{1 + \rho {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}\mathit{\boldsymbol{h}}}}} \right) - {\rm{log}}\left( {\frac{1}{\tau }} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 + \frac{{\rho {P_A}\mathit{\boldsymbol{t}}_k^H\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}{t_k}}}{{1 + \rho \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}{\mathit{\boldsymbol{t}}_k} + \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{t}}_k}}} \le \frac{1}{\tau },\forall k \in K\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} {{P_0} + \rho ({P_A} {\rm{Tr}} (\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}) + {\rm{Tr}} (\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}})) + }\\ {{\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) \le \eta (1 - \rho )({P_A} {\rm{Tr}} (\mathit{\boldsymbol{f}}{\mathit{\boldsymbol{f}}^{\rm{H}}}) + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Tr}} ({\mathit{\boldsymbol{H}}_{{\rm{RR}}}}\mathit{\boldsymbol{H}}_{{\rm{RR}}}^{\rm{H}})(\rho ({P_A} {\rm{Tr}} (\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}) + \\ \begin{array}{*{20}{c}} { {\rm{Tr}} (\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}})) + {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}))\eta (1 - \rho )({P_A} {\rm{Tr}} (\mathit{\boldsymbol{f}}{\mathit{\boldsymbol{f}}^{\rm{H}}}) + }\\ {{\rm{Tr}} ({\mathit{\boldsymbol{H}}_{{\rm{RR}}}}\mathit{\boldsymbol{H}}_{{\rm{RR}}}^{\rm{H}}) \times (\rho ({P_A} {\rm{Tr}} (\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}) + {\rm{Tr}} (\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}})) + } \end{array}\\ \begin{array}{*{20}{c}} { {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}))) \ge {P_{R,{\rm{min}}}}\rho {P_A} {\rm{Tr}} ({\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{Wf}}{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{W}}^{\rm{H}}}\mathit{\boldsymbol{g}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho {\rm{Tr}} ({\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}\mathit{\boldsymbol{g}}) + {\rm{Tr}} ({\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} g}}) \ge {P_{C,{\rm{min}}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}_{{\rm{RR}}}}\mathit{\boldsymbol{W}} = {\bf{0}}} \end{array} \end{array} $ | (18) |
其中为系统运行消耗的能量.根据恒等式Tr(BHCDE)=vec(B)H(ET(C)vec(D)以及公式Tr(BC)=Tr(CB),可以将公式(18)转化为
| $ R_s^* = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{W}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \succeq 0} {\rm{log}}\left( {1 + \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Aw}}}}{{1 + {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Bw}}}}} \right) - {\rm{log}}\left( {\frac{1}{\tau }} \right) $ | (19a) |
| $ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{log}}\left( {1 + \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{C}}_{1,k}}\mathit{\boldsymbol{w}}}}{{1 + \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{t}}_k} + {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{C}}_{2,k}}\mathit{\boldsymbol{w}}}}} \right) \le {\rm{log}}\left( {\frac{1}{\tau }} \right),}\\ {\forall k \in K} \end{array} $ | (19b) |
| $ {P_0} + {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Dw}} + {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) \le {\rm{M}} + {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Kw}} + L{\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) $ | (19c) |
| $ {{\rm{M}} + {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Kw}} + {\rm{LTr}}(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) \ge {P_{R,{\rm{min}}}}} $ | (19d) |
| $ {{\mathit{\boldsymbol{w}}^{\rm{H}}}({\mathit{\boldsymbol{A}}_g} + {\mathit{\boldsymbol{B}}_g})\mathit{\boldsymbol{w}} + {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} g}} \ge {P_{C,{\rm{min}}}}} $ | (19e) |
| $ {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}_{{\rm{RR}}}}\mathit{\boldsymbol{W}} = {\bf{0}}} $ | (19f) |
其中:w=vec(W);vec(·)为矩阵的列向量化操作;A=ρPA((f*fT)⊗(hhH));Ag=ρPA((f*fT)⊗(ggH));B=ρIN⊗(hhH);Bg=ρIN⊗(ggH);M=η(1-ρ)PA
| $ {R_S^* = \mathop {{\rm{max}}}\limits_\tau {\rm{log}}(1 + v(\tau )) - {\rm{log}}\left( {\frac{1}{\tau }} \right)} $ | (20a) |
| $ {{\rm{ s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\tau _{{\rm{min}}}} \le \tau \le 1} $ | (20b) |
其中τmin为单变量τ的下界.由式(19b)可知,τ≤1,即τmax=1.固定τ,内层优化问题的最优目标值为
| $ {v(\tau ) = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{w}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \succeq 0} \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Aw}}}}{{\mathit{\boldsymbol{1 + }}{\mathit{\boldsymbol{w}}^{\rm{H}}}Bw}}} $ | (21a) |
| $ {1 + \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{C}}_{1,k}}\mathit{\boldsymbol{w}}}}{{1 + \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{t}}_k} + {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{C}}_{2,k}}\mathit{\boldsymbol{w}}}} \le \frac{1}{\tau },\forall k \in K} $ | (21b) |
| $ {{\rm{ 式 }}({\rm{19c}})\backsim ({\rm{19f}})} $ | (21c) |
根据式(20a)可知,系统要得到正的安全速率,必须满足
| $ \tau \ge {(1 + {\gamma _B})^{ - 1}} $ | (22) |
因此,只要求出目的节点B的最大信干噪比γB,就能求出τ的下界τmin.则γB的优化问题为
| $ {{\gamma _B} = \mathop {{\rm{max}}}\limits_w \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Aw}}}}{{1 + {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Bw}}}}} $ | (23a) |
| $ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Dw}} \le {P_{{\rm{max}}}}} $ | (23b) |
通过验证,当式(23)取得最优目标值时,约束条件(23b)的等式成立,即wHDw=Pmax.因此,式(22)和下面的广义Rayleigh熵问题等价
| $ {\gamma _B} = \mathop {{\rm{max}}}\limits_w \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Aw}}}}{{{\mathit{\boldsymbol{w}}^{\rm{H}}}(\mathit{\boldsymbol{D}}/{P_{{\rm{max}}}} + \mathit{\boldsymbol{B}})\mathit{\boldsymbol{w}}}} $ | (24) |
γB=PAuH(D/Pmax+B)-1u为式(23)的最优目标值,u=f*⊗h.
外层问题(20)是一个单变量优化问题,可以通过一维搜索求得最优的τ.与此同时,式(21)仍然是非凸的.接下来,将半定松弛(SDR, semi-definite relaxation)[13]求解问题(21).
根据Luo等[14]半定松弛技术的思想,定义W=wwH和rank(W)=1.按照SDR的标准程序,去掉非凸限制rank(W)=1,问题(21)转化为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_{{\rm{ relax }}}}(\alpha ) = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{\bar W}} \succeq 0,\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \succeq {\bf{0}}} \frac{{ {\rm{Tr}} (\mathit{\boldsymbol{A}}{\kern 1pt} \mathit{\boldsymbol{\bar W}})}}{{1 + {\rm{Tr}} (\mathit{\boldsymbol{B}}{\kern 1pt} \mathit{\boldsymbol{\bar W}})}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\rm{ s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Tr}} (({\mathit{\boldsymbol{C}}_{1,k}} - \alpha {\mathit{\boldsymbol{C}}_{2,k}})\mathit{\boldsymbol{\bar W}}) - \alpha {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{t_k}\mathit{\boldsymbol{t}}_k^{\rm{H}}) \le \alpha ,}\\ {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall k \in K} \end{array}\\ \begin{array}{*{20}{c}} {{P_0} + {\rm{Tr}} (\mathit{\boldsymbol{D}}{\kern 1pt} \mathit{\boldsymbol{\bar W}}) + {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) \le M + {\rm{Tr}} (\mathit{\boldsymbol{K}}{\kern 1pt} \mathit{\boldsymbol{\bar W}}) + L{\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }})}\\ {{\rm{M}} + {\rm{Tr}} (\mathit{\boldsymbol{K}}{\kern 1pt} \mathit{\boldsymbol{\bar W}}) + L{\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) \ge {P_{R,{\rm{min}}}}} \end{array}\\ \begin{array}{*{20}{c}} { {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Tr}} (({\mathit{\boldsymbol{A}}_g} + {\mathit{\boldsymbol{B}}_g})\mathit{\boldsymbol{\bar W}}) + {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} g}}{\kern 1pt} {\mathit{\boldsymbol{g}}^{\rm{H}}}) \ge {P_{C,{\rm{min}}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{W}}{\kern 1pt} {\mathit{\boldsymbol{H}}_{{\rm{RR}}}}\mathit{\boldsymbol{W}} = {\bf{0}}} \end{array} \end{array} $ | (25) |
其中α=1/τ.利用Charnes-Cooper变换,把拟凸问题(25)转化为一个凸的半定规划(SDP, semi-definite program)问题.具体地讲,通过引入松弛变量μ≥0做变量替换,即令W=G/μ,Σ=J/μ.式(25)可以等价地转化为
| $ \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{G}},\mathit{\boldsymbol{J}},\mathit{\boldsymbol{\mu }}} {\rm{Tr}} (\mathit{\boldsymbol{AG}}) $ | (26a) |
| $ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \mu + {\rm{Tr}} (\mathit{\boldsymbol{BG}}) = 1 $ | (26b) |
| $ {\rm{Tr}} (({\mathit{\boldsymbol{C}}_{1,k}} - \alpha {\mathit{\boldsymbol{C}}_{2,k}})\mathit{\boldsymbol{G}}) - \alpha {\rm{Tr}} (\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{t}}_k}\mathit{\boldsymbol{t}}_k^{\rm{H}}) \le \mu \alpha ,\forall k \in K $ | (26c) |
| $ \mu {P_0} + {\rm{Tr}} (\mathit{\boldsymbol{DG}}) + {\rm{Tr}} (\mathit{\boldsymbol{J}}) \le \mu M + {\rm{Tr}} (\mathit{\boldsymbol{KG}}) + L{\rm{Tr}} (\mathit{\boldsymbol{J}}) $ | (26d) |
| $ {\mu M + {\rm{Tr}} (\mathit{\boldsymbol{KG}}) + L{\rm{Tr}} (\mathit{\boldsymbol{J}}) \ge \mu {P_{R,{\rm{min}}}}} $ | (26e) |
| $ { {\rm{Tr}} (({\mathit{\boldsymbol{A}}_g} + {\mathit{\boldsymbol{B}}_g})\mathit{\boldsymbol{G}}) + {\rm{Tr}} (\mathit{\boldsymbol{Jg}}{\mathit{\boldsymbol{g}}^{\rm{H}}}) \ge \mu {P_{C,{\rm{min}}}}} $ | (26f) |
| $ {\mathit{\boldsymbol{G}} \succeq {\bf{0}},\mathit{\boldsymbol{J}} \succeq {\bf{0}},\mu \ge 0} $ | (26g) |
| $ \mathit{\boldsymbol{W}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{H}}_{{\rm{RR}}}}\mathit{\boldsymbol{W}} = {\bf{0}} $ | (26h) |
经过公式转化后,式(26)成为了一个凸的SDP问题.此时可以非常高效地利用标准的优化软件包CVX[14]和SeDuMi编写matlab程序对公式进行求解,得到式(26)的最优解(G*, J*, μ*).
至此,求解出到问题(26)的最优解(G*, J*, μ*),意味着内层优化问题求解完毕.接下来还需要再一次根据关系式W=G/μ、Σ=J/μ,得到式(25)的最优解(W*, Σ*).然而在重写问题(25)的时候丢掉了非凸限制rank(W)=1,那么问题(25)的解可能不是原始非凸问题(21)的解.下面,验证问题(25)的最优解始终满足rank(W)=1的要求.具体地讲,考虑下面的功率最小化问题
| $ \mathop {{\rm{min}}}\limits_{\bar W \succeq 0,\Sigma \succeq 0} {\rm{Tr}} (\mathit{\boldsymbol{D}}{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar W}}) $ | (27a) |
| $ \begin{array}{*{20}{l}} {{\rm{ s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Tr}} (({\mathit{\boldsymbol{C}}_{1,k}} - \alpha {\mathit{\boldsymbol{C}}_{2,k}})\mathit{\boldsymbol{\bar W}}) - \alpha {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{t}}_{\rm{k}}}\mathit{\boldsymbol{t}}_k^{\rm{H}}) \le \alpha ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall k \in K} \end{array} $ | (27b) |
| $ {P_0} + {\rm{Tr}} (\mathit{\boldsymbol{D}}{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar W}}) + {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) \le {\rm{M}} + {\rm{Tr}} (\mathit{\boldsymbol{K}}{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar W}}) + L{\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) $ | (27c) |
| $ {{\rm{M}} + {\rm{Tr}} (\mathit{\boldsymbol{K}}{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar W}}) + L{\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) \ge {P_{R,{\rm{min}}}}} $ | (27d) |
| $ { {\rm{Tr}} (({\mathit{\boldsymbol{A}}_g} + {\mathit{\boldsymbol{B}}_g})\mathit{\boldsymbol{\bar W}}) + {\rm{Tr}} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}g{\mathit{\boldsymbol{g}}^{\rm{H}}}) \ge {P_{C,{\rm{min}}}}} $ | (27e) |
| $ { {\rm{Tr}} ((\mathit{\boldsymbol{A}} - {v_{{\rm{ relax }}}}(\alpha )\mathit{\boldsymbol{B}})\mathit{\boldsymbol{\bar W}}) \ge {v_{{\rm{ relax }}}}(\alpha )} $ | (27f) |
| $ {\mathit{\boldsymbol{W}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{H}}_{{\rm{ RR }}}}\mathit{\boldsymbol{W}} = {\bf{0}}} $ | (27g) |
其中υrelax(α)是式(25)的最优目标值,它在式(27)中被认为是已知常数,根据Tr(A W)/1+Tr(B W)得到式(27f).
引理1 式(27)的最优解也是式(25)的最优解.
命题1 如果该系统存在正的安全速率,那么可以推出问题(25)总是存在最优解(W*, Σ*),满足rank(W)=1的要求.则式(21)的紧松弛问题是问题(25),且可以通过问题(27)得到该问题的最优解.
2.2 求解算法描述根据计算演算和分析,可以设计双层优化问题式(20)和(21)的求解算法.算法的求解思路是:给定τ,通过求式(26)的解得到内层优化式(21)的最优目标值υ(τ).双层优化问题的求解如算法1所示.
算法1 双层优化问题求解算法
输入:a=(1+PAuH(D/Pmax+B)-1u)-1,b=1,u=f*⊗h,一维搜索精度ζ,各个随机信道.
输出:局部最优解(W*, Σ*)和
1 l=a+0.382(b-a),u=a+0.618(b-a),求优化式(26)的解,得到ϕl=ϕ(1/l-1),ϕu=ϕ(1/u-1),然后用ϕl和ϕu分别代替υ(τ),计算式(20),分别得到R(l)和R(u);
2 while(b-a)>ζ
3 if (R(l) < R(u)) then
a=l, l=u, ϕl=ϕu, u=a+0.618(b-a),求优化式(26)的解, 得到ϕu=ϕ(1/u-1),然后用ϕu代替υ(τ),最后计算式(20)的值,得到Ru;
4 else
b=u, u=l, ϕu=ϕl, l=a+0.382(b-a), 求优化式(26)的解, 得到ϕl=ϕ(1/l-1),然后用ϕl代替υ(τ),最后计算式(20)的值,得到Rl;
5 end if
6 end while
7 τ=(a+b)/2,把α=(1/τ-1)代入式(26)中进行求解,得到目标值ϕ(α)和最优解(W*, Σ*).接下来用ϕ(α)代替ϕ(τ),最后计算式(20)得到
8 if rank(W)≥2 then
求式(27)的解,得到最优解(W*, Σ*);
9 end if
10 分解矩阵W=w wH,得到W*=vec-1(w);
11 输出局部最优解(W*, Σ*)和
至此,得到了最优解(W*, Σ*).重写问题(17)为
| $ \begin{array}{*{20}{c}} {R_S^* = \mathop {{\rm{max}}}\limits_\rho {\rm{log}}\left( {1 + \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Aw}}}}{{1 + {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Bw}}}}} \right) - }\\ {{\rm{log}}\left( {1 + \frac{{{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{C}}_{\rm{1}}}\mathit{\boldsymbol{w}}}}{{1 + \mathit{\boldsymbol{t}}_k^{\rm{H}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{t}}_k} + {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{C}}_{\rm{2}}}\mathit{\boldsymbol{w}}}}} \right)}\\ {{\rm{ s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < \rho < 1} \end{array} $ | (28) |
因为ρ的变量区间长度小于1,所以可以很方便地运用一维搜索方法找到最优的ρ*,最后根据式(28)求出最优目标值
采用蒙特卡洛实验方法对所提出方法的安全速率进行仿真验证.具体地讲,将所提出方法与人工噪声方法和无人工噪声方法进行比较.人工噪声方法是指:中继节点在转发数据的同时发送人工噪声,但是在目的节点处不能将人工噪声消除;而无人工噪声方法是指:在中继节点转发数据时不发送噪声,即内层优化问题的能量信号协方差矩阵Σ=0.
仿真实验参数设置如下:源节点A发射功率PA=10 dB,中继节点发射和接收天线M=N=3,中继节点所需能量的最小值PR, min=10 dB,能量收集节点C收集能量的最小值PC, min=1 dB,能量转换效率η=80%,窃听节点个数K=3.所有仿真结果都是1 000次随机信道得到实验结果的平均值,信道设置为瑞利衰减信道.
图 2给出了在源节点功率变化时3种方法安全速率的比较.从实验结果可以看出,随着源节点发射功率的增加,3种方法的安全速率均增加.当PA=35 dB时,所提出的方法比人工噪声方法和无噪声方法分别高出0.506 6 dBm和0.646 5 dBm.在源节点发射功率较小时,人工噪声方法和无噪声方法的性能相近,但人工噪声方法略微优于无人工噪声方法.这表明在源节点发射功率较小时应该将大部分功率用于转发数据,系统的安全速率才能提高.观察图 2可以看出,所提出的方法的安全速率明显高于其他2种方法,并且其优势随着源节点的发射功率增大而增大.人工噪声方法与无噪声方法相比,提高的幅度不大,这是因为中继发射人工噪声干扰窃听节点的同时也降低了目的节点的信干燥比,而本文提出的方法在显著降低窃听信道质量的同时不会对合法信道造成影响.
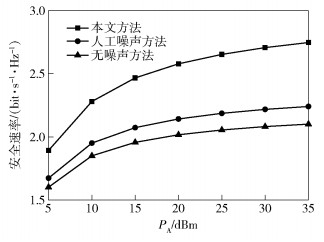
|
图 2 源节点功率变化时不同方法的安全性能的比较 |
图 3给出了在中继节点所需能量的最小值变化时3种方法安全速率的比较.从图中可以看出,当PR, min≤30 dB时,3种方法的安全速率均没有变化,本文提出的方法的安全速率明显高于其他2种方法.其原因在于中继节点转发数据所需的能量较小,不会对目的节点的信干噪比造成影响,且中继采用全双工工作方式可以从自干扰信号中收集能量提高了中继节点收集能量的效率.当PR, min≥30 dB时,3种方法的安安全性能均有所降低.这是因为中继节点收集能量较多使中继转发信号的功率较少,降低了目的节点的信干噪比,从而降低了系统的安全速率.
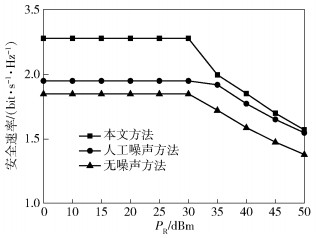
|
图 3 中继节点所需能量的最小值对安全速率的影响 |
图 4给出了在能量收集节点C所需能量最小值变化时3种方法安全速率的比较.从比较的结果可以看出,随着能量收集节点C所需能量的最小值不断增大,所提出的方法的安全性能微弱的减小,而其他2种方法的安全性能急剧减小.随着能量收集节点C所需能量最小值的增大,所提出方法的优势越来越明显.这表明在中继处发射能量信号有利于能量收集节点收集能量.此外,采用本文所提出方法,在系统中增加能量收集节点对系统的安全速率影响非常小,而其他2种方法对系统的安全速率产生的影响很大.
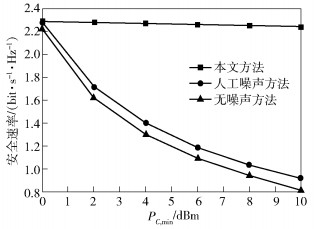
|
图 4 能量收集节点C所需能量的最小值对安全速率的影响 |
图 5给出了在中继节点天线数量不同情况下的3种方法安全速率的比较.从图中可以看出,在实验参数相同情况下,所提出的方法与其他2种方法相比在安全速率上有显著优势.随着天线数量的增加,3种方法的安全性能均不断增大.这表明随着天线数目不断增大,中继节点拥有的空间自由度不断增大,使其可以根据窃听节点的信道状态信息,越来越有针对性地降低窃听信道的信道质量,且应用大规模天线阵列有利于中继收集能量,使得中继节点传输功率增大.
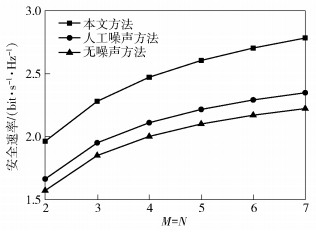
|
图 5 中继节点天线数量对安全速率的影响 |
图 6给出了在窃听节点个数不同时3种方法安全速率的比较.从图中可以看出,随着窃听节点数量的越来越多,3种方法的安全速率均有所下降,但笔者所提出方法的安全速率始终比其他2种方法高,并且无噪声方法的安全速率下降的最快.因此在窃听节点较多时,利用能量信号和人工噪声可以有针对性地干扰窃听信道.人工噪声降低了窃听信道的质量,对合法信道产生了较小的干扰,提高了系统的安全速率.而能量信号在降低窃听信道的质量的同时并没有对合法接收信道造成影响,所以能量信号更有效地提高了系统的安全速率.
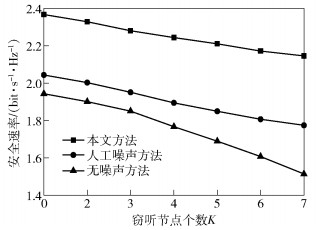
|
图 6 窃听节点的个数对安全速率的影响 |
在能量受限的全双工中继系统中,存在多个窃听节点情况下的安全传输问题,提出了一种新的基于能量和信息联合传输的安全波束成形方法.通过联合优化能量信号协方差矩阵、波束成形向量和功率分配因子,达到系统安全速率最大化的目标.采用双层优化方法、一维搜索方法和半定松弛技术解决了该非凸优化问题.同时证明了松弛问题总是存在秩为1的最优解,即所采用的半定松弛是紧的.仿真实验结果表明,所提出方法的安全性能明显优于人工噪声方法和无噪声方法.
| [1] |
Zou Y L, Zhu J, Wang X B, et al. A survey on wireless security:Technical challenges, recent advances, and future trends[J]. Proceedings of IEEE, 2016, 104(9): 1727-1765. DOI:10.1109/JPROC.2016.2558521 |
| [2] |
Krikidis I, Thompson J S, Mclaughlin S. Relay selection for secure cooperative networks with jamming[J]. IEEE Transactions on Wireless Communications, 2013, 2(4): 5003-5011. |
| [3] |
Liu G, Yu F R, Ji H, et al. In-band full-duplex relaying:a survey, research issues and challenges[J]. IEEE Communications Surveys & Tutorials, 2017, 17(2): 500-524. DOI:10.1109/COMST.2015.2394324 |
| [4] |
Li Q, Yang Y, Ma W K, et al. Robust cooperative beamforming and artificial noise design for physical-layer secrecy in AF multi-antenna multi-relay networks[J]. IEEE Transactions on Signal Processing, 2014, 63(1): 206-220. |
| [5] |
Sun Y, Ng D W K, Zhu J, et al. Multi-objective optimization for robust power efficient and secure full-duplex wireless communication systems[J]. IEEE Transactions on Wireless Communications, 2015, 15(8): 5511-5526. |
| [6] |
张立健, 金梁, 刘璐, 等. 多天线中继系统中人工噪声辅助的安全波束成形[J]. 通信学报, 2014, 35(11): 81-88. Zhang Lijian, Jin Liang, Liu Lu, et al. Artificial noise aided secure beamforming for muli-antenna relay systems[J]. Journal on Communications, 2014, 35(11): 81-88. |
| [7] |
Ulukus S, Yener A, Erkip E. Energy harvesting wireless communications:a review of recent advances[J]. IEEE Journal. on Selected Areas in Communications, 2015, 33(3): 360-381. DOI:10.1109/JSAC.2015.2391531 |
| [8] |
Lu X, Wang P, Niyato D, et al. Wireless networks with RF energy harvesting:a contemporary survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 757-789. DOI:10.1109/COMST.2014.2368999 |
| [9] |
Özlem T D, Tuncer T E. Robust optimum and near-optimum beamformers for decode-and-forward full-duplex multi-antenna relay with self-energy recycling[J]. IEEE Transactions on Wireless Communications, 2019, 18(3): 1566-1580. DOI:10.1109/TWC.2019.2893667 |
| [10] |
Xing H, Liu L, Zhang R. Secrecy wireless information and power transfer in fading wiretap channel[J]. IEEE Transactions on Vehicular Technology, 2014, 65(1): 180-190. |
| [11] |
Zhao M, Wang X, Feng S. Joint power splitting and secure beamforming design in the multiple non-regenerative wireless-powered relay networks[J]. IEEE Communications Letters, 2015, 19(9): 1540-1543. DOI:10.1109/LCOMM.2015.2453161 |
| [12] |
Feng Y, Yang Z, Zhu W P, et al. Robust cooperative secure beamforming for simultaneous wireless information and power transfer in amplify-and-forward relay networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 2354-2366. DOI:10.1109/TVT.2016.2578313 |
| [13] |
Luo Z Q, Ma W K, So M C, et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine, 2010, 27(3): 20-34. |
| [14] |
Grant M, Boyd S. Matlab software for disciplined convex programming[EB/OL]. 2008(2009-10-01)[2019-01-04]http://cvxr.com/cvx.
|



