在传输线系统电磁脉冲(EMP)响应的精确计算中,通常必须将端接负载的频变效应考虑在内,为此提出了一种端接频变负载传输线系统电磁脉冲响应的数值算法.首先,应用矢量网络分析仪或阻抗分析仪测试或计算得到端接频变负载电路的幅频特性和相频特性;然后,应用矢量匹配(VF)法对幅频特性和相频特性进行拟合,得到一系列极点、留数和常数项;最后,结合拟合得到的数据,应用时域有限差分(FDTD)法建立端接频变负载传输线系统的数值模型,并应用到分段线性递归卷积技术以提高卷积计算效率.所提算法具有较高的计算效率和精度,可应用于多种端接频变负载传输线系统电磁脉冲响应计算.
In the calculation of transmission line systems response to electromagnetic pulse (EMP), the frequency-dependent effect of terminated loads should be considered. A numerical algorithm for a transmission line system terminated with frequency-dependent loads exposed to EMP is proposed. Firstly, the amplitude-frequency characteristics and phase-frequency characteristics of frequency-dependent loads are captured by vector network analyzer. Then the measured data are expressed by a series of rational formulas based on residuals and poles derived by vector fitting (VF) method. Lastly discrete equations for the system are derived based on finite-difference time-domain (FDTD) method. In the proposed algorithm, piecewise linear recursive convolution technique is employed to simplify the computation of convolution formulas. The simulated results show a well consistency with the theory. Compared the other algorithm, this method increases the efficiency and accuracy, and has a broad application prospect in frequency-dependent systems.
传输线系统的电磁耦合问题是任何电力、电子系统电磁脉冲(EMP,electromagnetic pulse)效应研究的重要组成部分.在高频电磁干扰条件下,传输线端接负载通常会呈现出频变效应,即其等效阻抗或导纳会随频率的变化而变化.目前,国内外学者对于传输线电磁耦合问题已进行了大量研究[1-5],但多数都将端接负载等效为纯电阻、电感等线性负载,所取得结果与实际情况差别较大.为精确计算传输线系统的电磁脉冲响应,必须考虑其端接负载的频变效应. Huang等[6]和杨雨川等[7-8]基于戴维南等效电路方法求解单端端接频变负载传输线的电磁脉冲响应,但该方法只能用于单导体传输线系统,且频变负载电路形式较简单.吴振军等[5]和Paul[9]应用状态变量法对端接频变负载传输线系统进行求解,但该方法仅限于频变负载以具体电路形式表示时才能应用,若频变负载电路复杂,则列写状态方程极为困难.
在研究对象端口处的电压和电流关系已知的情况下,Liu等[10]和Watanabe等[11]应用时域有限差分(FDTD, finite-difference time-domain)法对非线性负载进行了分析.但在大多数实际情况下,待研究负载端口处的电压和电流关系并非已知的,例如电力系统中的电机和变压器等. Xia等[12]和Gustavsen等[13]采用分段线性递归卷积(PLRC, piecewise linear recursive convolution)技术提高了FDTD法建模计算精度,加快了计算效率.
对于频变系统的建模,矢量匹配(VF, vector fitting)法[14]是一种有力的工具.笔者将矢量匹配法引入到FDTD法之中,提出了一种求解端接频变负载多导体传输线系统电磁脉冲响应的数值算法.
1 矢量匹配法及端接频变负载传输线建模 1.1 矢量匹配法的主要步骤矢量匹配法的具体拟合步骤主要有3步[14-15]:①待拟合电路网络函数(计算或实验测量得到)极点的确定;②相应函数留数的确定;③初始极点与拟合阶数的选择,需要根据待拟合对象的复杂程度确定.
1.2 端接频变负载传输线建模传输线理论是一种求解传输线系统电磁脉冲响应的有效方法.对架设于非理想导电地面上方的传输线系统进行电磁暂态计算时,必须考虑大地阻抗对传输线系统分布参数的影响,且激励场必须考虑地面反射的影响[7, 9].
图 1中,Ei为入射均匀平面波电场,其俯仰角、方位角和极化角分别为θp、ϕp和θE.由Snell公式可得地面对入射波的垂直极化和水平极化反射系数Rv和Rl[9].

|
图 1 外界电磁场辐照传输线示意图 |
依据图 1所示坐标系统,忽略导线内阻抗和大地导纳的影响(研究表明这两种参数对于架空线影响可忽略),外界电磁场激励下基于Agrawal模型的N+1导体传输线频域电报方程为[7]
| $ {\frac{{{\rm{d}}{\mathit{\boldsymbol{V}}^s}(z)}}{{{\rm{d}}z}} + {\mathit{\boldsymbol{Z}}_g}(\omega )\mathit{\boldsymbol{I}}(z) + {\rm{j}}\omega \mathit{\boldsymbol{LI}}(z) = \mathit{\boldsymbol{V}}_F^s(z)} $ | (1) |
| $ {\frac{{{\rm{d}}\mathit{\boldsymbol{I}}(z)}}{{{\rm{d}}z}} + {\rm{j}}\omega \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{V}}^s}(z) = 0} $ | (2) |
其中:Vs(z)和I(z)分别为沿线感应散射电压和电流,Zg(ω)为架空线的大地阻抗,L和C分别为架空线的单位长度分布电感和电容,VFs(z)为外界电磁场在传输线z处的等效分布电压源,计算如下:
| $ {\mathit{\boldsymbol{V}}_F^s(h,0,z) = \mathit{\boldsymbol{E}}_z^i(h,0,z) + \mathit{\boldsymbol{E}}_z^r(h,0,z)} $ | (3) |
其中:
| $ \mathit{\boldsymbol{V}}(z) = {\mathit{\boldsymbol{V}}^s}(z) - \mathop \smallint \nolimits_0^h [\mathit{\boldsymbol{E}}_x^i(x,0,z) + \mathit{\boldsymbol{E}}_x^r(x,0,z)]{\rm{d}}x $ | (4) |
其中
为了求得式(1)和式(2)所示方程的唯一解,必须加入由垂直电场在负载端形成的等效集总电压源以及确定关于负载的电压和电流边界条件.传输线两端负载处由垂直电场形成的等效集总电压源分别为[9]
| $ {\mathit{\boldsymbol{V}}_0}\mathop \smallint \nolimits_0^h [\mathit{\boldsymbol{E}}_x^i(x,0,0) + \mathit{\boldsymbol{E}}_x^r(x,0,0)]{\rm{d}}x $ | (5a) |
| $ {\mathit{\boldsymbol{V}}_l}\mathop \smallint \nolimits_0^h [\mathit{\boldsymbol{E}}_x^i(x,0,l) + \mathit{\boldsymbol{E}}_x^r(x,0,l)]{\rm{d}}x $ | (5b) |
终端边界条件为[9]
| $ {{\mathit{\boldsymbol{V}}^s}(0) = - {\mathit{\boldsymbol{R}}_s}\mathit{\boldsymbol{I}}(0) + {\mathit{\boldsymbol{V}}_0}} $ | (6a) |
| $ {{\mathit{\boldsymbol{V}}^s}(l) = {\mathit{\boldsymbol{R}}_l}\mathit{\boldsymbol{I}}(l) + {\mathit{\boldsymbol{V}}_l}} $ | (6b) |
| $ {\mathit{\boldsymbol{E}}^i} = {\mathit{\boldsymbol{E}}_0}({e_x}{\mathit{\boldsymbol{a}}_x} + {e_y}{\mathit{\boldsymbol{a}}_y} + {e_z}{\mathit{\boldsymbol{a}}_z}){{\rm{e}}^{ - {\rm{j}}({\beta _x}x - {\beta _y}y - {\beta _z}z)}} $ | (7) |
其中:ex、ey和ez分别为入射场的电场矢量E0在直角坐标系x、y和z轴方向上的分量;βx、βy和βz分别为直角坐标系x、y和z轴方向上的相位常数分量.这些量的计算祥参Paul [9]. ax、ay和az分别为x、y和z轴方向上的单位矢量.
由式(1)和式(7)可计算得到入射波反射电场的频域表达式Er.由于架空线的截面尺寸远小于入射波波长,将Ei和Er代入式(3)~式(6),可得均匀平面波激励时VFs(z)、V0和Vl的频域表达式为
| $ {\mathit{\boldsymbol{V}}_F^s(z) \approx {\mathit{\boldsymbol{E}}_0}(\omega )f(\omega ){{\rm{e}}^{ - {\rm{j}}{\beta _z}z}}} $ | (8a) |
| $ {{\mathit{\boldsymbol{V}}_0}(\omega ) \approx {\mathit{\boldsymbol{E}}_0}(\omega )g(\omega )} $ | (8b) |
| $ {{\mathit{\boldsymbol{V}}_l}(\omega ) \approx {\mathit{\boldsymbol{E}}_0}(\omega ){{\rm{e}}^{ - {\rm{j}}{\beta _z}l}}} $ | (8c) |
其中:f(ω)≈ez1(1-Rv)+ez2(1+Rh),g(ω)≈exh(1+Rh),ez1=-sin θEcos θpsin ϕp,ez2=cos θEcos ϕp,ex=sin θEsin θp,βz=
为便于瞬态分析,在复频域中应用矢量匹配法将架空多导体传输线的频域形式大地阻抗Zg以及f(ω)、g(ω)分别展开为如下形式:
| $ {{\mathit{\boldsymbol{Z}}_{gij}} = \sum\limits_{s = 1}^{NF} {\frac{{s{c_{ijs}}}}{{s - {a_{ijs}}}}} } $ | (9a) |
| $ {f = {d_2} + \sum\limits_{s = 1}^{NF} {\frac{{{c_{2s}}}}{{s - {a_{2s}}}}} } $ | (9b) |
| $ {g = {d_3} + \sum\limits_{s = 1}^{NF} {\frac{{{c_{3s}}}}{{s - {a_{3s}}}}} } $ | (9c) |
其中:cijs(i, j=1, 2, …, N)、c2s和c3s分别为Zgij、f和g的第s个极点,aijs、a2s和a3s分别为Zgij、f和g的第s个留数,d2和d3分别为应用矢量匹配法对f和g进行拟合得到的常数项;NF为矢量匹配法的拟合阶数.将式(9)进行Laplace逆变换,得到其时域形式,可以方便地进行时域卷积计算.
将式(9)代入式(1)和式(2),再变换到时域,可以分别得到如下时域电报方程:
| $ \begin{array}{*{20}{c}} {\frac{{\partial {\mathit{\boldsymbol{V}}^s}(z,t)}}{{\partial z}} + \mathit{\boldsymbol{L}}\frac{{\partial \mathit{\boldsymbol{I}}(z,t)}}{{\partial t}} + \mathit{\boldsymbol{Z}}_g^\prime (t)\frac{{\partial \mathit{\boldsymbol{I}}(z,t)}}{{\partial t}} = }\\ {\left( {{d_2} \cdot \delta (t) + \sum\limits_{s = 1}^{NF} {{c_{2s}}} {{\rm{e}}^{{a_{2s}}t}}} \right){\mathit{\boldsymbol{E}}_0}\left( {t - \frac{z}{{{v_z}}}} \right)} \end{array} $ | (10a) |
| $ \frac{{\partial \mathit{\boldsymbol{I}}(z,t)}}{{\partial z}} + \mathit{\boldsymbol{C}}\frac{{\partial {\mathit{\boldsymbol{V}}^s}(z,t)}}{{\partial t}} = 0 $ | (10b) |
其中:δ(t)为冲激函数,E0为辐照传输线系统的瞬态电场的时域形式.
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Z}}_g^\prime (t) = \\ \left[ {\begin{array}{*{20}{c}} {\sum\limits_{s = 1}^{NF} {{c_{11s}}} {{\rm{e}}^{{a_{11s}}t}}}&{\sum\limits_{s = 1}^{NF} {{c_{12s}}} {{\rm{e}}^{{a_{12s}}t}}}& \cdots &{\sum\limits_{s = 1}^{NF} {{c_{1Ns}}} {{\rm{e}}^{{a_{1Ns}}t}}}\\ {\sum\limits_{s = 1}^{NF} {{c_{21s}}} {{\rm{e}}^{{a_{21s}}t}}}&{\sum\limits_{s = 1}^{NF} {{c_{22s}}} {{\rm{e}}^{{a_{22s}}t}}}& \cdots &{\sum\limits_{s = 1}^{NF} {{c_{2Ns}}} {{\rm{e}}^{{a_{2Ns}}t}}}\\ \vdots & \vdots & \vdots & \vdots \\ {\sum\limits_{s = 1}^{NF} {{c_{N1s}}} {{\rm{e}}^{{a_{N1s}}t}}}&{\sum\limits_{s = 1}^{NF} {{c_{N2s}}} {{\rm{e}}^{{a_{N2s}}t}}}& \cdots &{\sum\limits_{s = 1}^{NF} {{c_{NNs}}} {{\rm{e}}^{{a_{NNs}}t}}} \end{array}} \right]N \times N \end{array} $ |
为运用矢量匹配法拟合得到的大地阻抗时域表达式,为表述简便,将其简记为
此处以N+1导体传输线(其中一个为参考导体)为例,建立端接频变负载的多导体传输线FDTD迭代公式.传输线始端端接纯阻性负载矩阵,末端信号导体与参考导体之间端接负载都为频变负载,信号导体之间没有负载连接.为表述方便,将散射电压记为M.
2 传输线始端电压迭代模型设M0为由外场在传输线始端等效的集总电压源,M1为负载端感应电压,根据式(6)及Paul[9]可得纯阻性负载端电流为I0=
应用一阶中心差分方法对其进行离散可得
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{I}}_0^{n + 0.5} = \mathit{\boldsymbol{R}}_s^{ - 1}(\mathit{\boldsymbol{M}}_0^{n + 0.5} - \mathit{\boldsymbol{M}}_1^{n + 0.5}) = }\\ {5\mathit{\boldsymbol{R}}_s^{ - 1}\left[ {(\mathit{\boldsymbol{M}}_0^{n + 1} + \mathit{\boldsymbol{M}}_0^n) - (\mathit{\boldsymbol{M}}_1^{n + 1} + \mathit{\boldsymbol{M}}_1^n)} \right]} \end{array} $ | (11) |
应用一阶中心差分法对式(10b)进行离散可得
| $ \frac{{\mathit{\boldsymbol{I}}_1^{n + 0.5} - \mathit{\boldsymbol{I}}_0^{n + 0.5}}}{{\Delta z/2}} + \mathit{\boldsymbol{C}}\frac{{\mathit{\boldsymbol{M}}_1^{n + 1} - \mathit{\boldsymbol{M}}_1^n}}{{\Delta t}} = 0 $ | (12) |
将式(11)代入式(12),化简可得传输线始端散射电压表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_1^{n + 1} = {\left( {{\mathit{\boldsymbol{R}}_s}\mathit{\boldsymbol{C}}\frac{{\Delta z}}{{\Delta t}} + {{\bf{1}}_{N \times N}}} \right)^{ - 1}}\left[ {\left( {{\mathit{\boldsymbol{R}}_s}\mathit{\boldsymbol{C}}\frac{{\Delta z}}{{\Delta t}} - {{\bf{1}}_{N \times N}}} \right) \times } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{M}}_1^n - 2{\mathit{\boldsymbol{R}}_s}\mathit{\boldsymbol{I}}_1^{n + 0.5} + 2\mathit{\boldsymbol{M}}_0^{n + 0.5}} \right] \end{array} $ | (13) |
其中
| $ \mathit{\boldsymbol{M}}_0^{n + 0.5} = {d_3}\mathit{\boldsymbol{E}}_0^{n + 0.5} + \sum\limits_{s = 1}^{NF} {\mathit{\boldsymbol{f}}_{1s}^n} $ | (14) |
其中
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{f}}_{1s}^n = \sum\limits_{m = 0}^n {\mathit{\boldsymbol{E}}_0^{n + 0.5 - m}} {c_{3s}}({{\rm{e}}^{{a_{3s}}(m + 1)\Delta t}} - {{\rm{e}}^{{a_{3s}}m\Delta t}})/{a_{3s}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{E}}_0^{n + 0.5}{c_{3s}}({{\rm{e}}^{{a_{3s}}\Delta t}} - 1)/{a_{3s}} + {{\rm{e}}^{{a_{3s}}\Delta t}}\mathit{\boldsymbol{f}}_{1s}^{n - 1}} \end{array} $ | (15) |
因为m是从0开始,而n是从1开始,所以f初值不为0,
传输线沿线各点散射电压公式推导较为简单,这里直接给出:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}_k^{n + 1} = \mathit{\boldsymbol{M}}_k^n - \frac{{\Delta t}}{{\Delta z}}{\mathit{\boldsymbol{C}}^{ - 1}}(\mathit{\boldsymbol{I}}_k^{n + 0.5} - \mathit{\boldsymbol{I}}_{k - 1}^{n + 0.5}),}\\ {k = 2,3, \cdots K} \end{array} $ | (16) |
其中K为传输线空间离散段数.
3 传输线末端电压迭代模型末端端接频变负载时,其感应电压公式推导非常复杂,下面进行详细说明.末端负载处电流为
| $ \mathit{\boldsymbol{I}}_L^{n + 0.5} = P(\mathit{\boldsymbol{M}}_{K + 1}^{n + 1} - \mathit{\boldsymbol{M}}_L^{n + 1}) + Q(\mathit{\boldsymbol{M}}_{K + 1}^n - \mathit{\boldsymbol{M}}_L^n) + \mathit{\boldsymbol{I}}_t^{n + 1} $ | (17) |
其中:P和Q表达式可参考文献[7],
| $ \mathit{\boldsymbol{I}}_t^n = \frac{1}{2}\sum\limits_{s = 1}^{{N_r}} {({\rho _s} + 1)} \mathit{\boldsymbol{I}}_{z,s}^n + \sum\limits_{s = {N_r} + 1}^{NF} { {\rm{Re}} } [({\rho _s} + 1)\mathit{\boldsymbol{I}}_{z,s}^n] $ | (18) |
其中:Nr为
传输线存在外场激励的情况下,
| $ \mathit{\boldsymbol{I}}_{z,s}^{n + 1} = ({x_{0,s}} - {\xi _{0,s}})\mathit{\boldsymbol{V}}_z^{n + 1} + {\xi _{0,s}}\mathit{\boldsymbol{V}}_z^n + {\rho _s}\mathit{\boldsymbol{I}}_{z,s}^n $ | (19) |
根据式(6b)可得,末端负载处电压为,其中ML为由垂直电场在末端负载处形成的等效集总电压源,其时域表达式为
| $ \mathit{\boldsymbol{M}}_L^n = {d_3}\mathit{\boldsymbol{E}}_0^{n - K\Delta z/{v_z}/\Delta t} + \sum\limits_{s = 1}^{NF} {\mathit{\boldsymbol{f}}_{2s}^n} $ | (20) |
其中
| $ \mathit{\boldsymbol{f}}_{2s}^n = \mathit{\boldsymbol{E}}_0^{n - K\Delta z/{v_z}/\Delta t}{c_{3s}}({{\rm{e}}^{{a_{3s}}\Delta t}} - 1)/{a_{3s}} + {{\rm{e}}^{{a_{3s}}\Delta t}}\mathit{\boldsymbol{f}}_{2s}^{n - 1} $ | (21) |
因为m是从0开始,而n是从1开始的,所以f的初始值为
| $ \mathit{\boldsymbol{f}}_{2s}^0 = \mathit{\boldsymbol{E}}_0^{ - K\Delta z/{v_z}\Delta t}{c_{3i}}({{\rm{e}}^{{a_{3i}}\Delta t}} - 1)/{a_{3i}} = 0 $ | (22) |
根据Watanabe等[11],传输线末端电压公式可离散为
| $ \frac{{(\mathit{\boldsymbol{I}}_L^{n + 1} + \mathit{\boldsymbol{I}}_L^n)/2 - \mathit{\boldsymbol{I}}_K^{n + 0.5}}}{{\Delta z/2}} + \mathit{\boldsymbol{C}}\frac{{\mathit{\boldsymbol{M}}_{K + 1}^{n + 1} - \mathit{\boldsymbol{M}}_{K + 1}^n}}{{\Delta t}} = 0 $ | (23) |
其中(
将频变负载两端的电压电流关系式(17)代入到式(23)中,可得负载端的展开式为
| $ \begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{G}}_1}(\mathit{\boldsymbol{M}}_{K + 1}^{n + 1} - \mathit{\boldsymbol{M}}_L^{n + 1}) + {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{M}}_{K + 1}^n - \mathit{\boldsymbol{M}}_L^n)}}{{\Delta z/2}} + }\\ {\frac{{\mathit{\boldsymbol{I}}_t^{n + 1} - \mathit{\boldsymbol{I}}_K^{n + 0.5}}}{{\Delta z/2}} + \mathit{\boldsymbol{C}}\frac{{\mathit{\boldsymbol{M}}_{K + 1}^{n + 1} - \mathit{\boldsymbol{M}}_{K + 1}^n}}{{\Delta t}} = 0} \end{array} $ | (24) |
其中:G1=diag[P P … P]N×N,G2=diag[Q Q … Q]N×N.变换式(24)形式可得频变负载端的电压表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{K + 1}^{n + 1} = {\left( {{\mathit{\boldsymbol{G}}_1} + \frac{{\mathit{\boldsymbol{C}}\Delta z}}{{2\Delta t}}} \right)^{ - 1}}\left[ {\left( {\frac{{\mathit{\boldsymbol{C}} \cdot \Delta z}}{{2\Delta t}} - {\mathit{\boldsymbol{G}}_2}} \right)\mathit{\boldsymbol{M}}_{K + 1}^n + } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{G}}_1}\mathit{\boldsymbol{M}}_L^{n + 1} + {\mathit{\boldsymbol{G}}_2}\mathit{\boldsymbol{M}}_L^n - \mathit{\boldsymbol{I}}_t^n + \mathit{\boldsymbol{I}}_K^{n + 0.5}} \right] \end{array} $ | (25) |
根据式(10a)可得
| $ \begin{array}{*{20}{c}} {\frac{{\mathit{\boldsymbol{M}}_{k + 1}^{n + 1} - \mathit{\boldsymbol{M}}_k^{n + 1}}}{{\Delta z}} + \mathit{\boldsymbol{L}}\frac{{\mathit{\boldsymbol{I}}_k^{n + 1.5} - \mathit{\boldsymbol{I}}_k^{n + 0.5}}}{{\Delta t}} + \mathit{\boldsymbol{Z}}_g^\prime (t)\frac{{\partial \mathit{\boldsymbol{I}}(z,t)}}{{\partial t}} = }\\ {\left[ {{d_2}\delta (t) + \sum\limits_{s = 1}^{NF} {{c_{2s}}} {{\rm{e}}^{{a_{2s}}t}}} \right]{\mathit{\boldsymbol{E}}_0}\left( {t - \frac{z}{{{v_z}}}} \right)} \end{array} $ | (26) |
式(26)中等号左边卷积项的表达式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Z}}_g^\prime (t)\frac{{\partial \mathit{\boldsymbol{I}}(z,t)}}{{\partial t}} = }\\ {\sum\limits_{m = 0}^n {\sum\limits_{s = 1}^{NF} {\frac{{{c_{ijs}}}}{{{a_{ijs}}\Delta t}}} } ({{\rm{e}}^{{a_{ijs}}(m + 1)\Delta t}} - {{\rm{e}}^{{a_{ijs}}m\Delta t}}) \times }\\ {(\mathit{\boldsymbol{I}}_k^{n + 1.5 - m} - \mathit{\boldsymbol{I}}_k^{n + 0.5 - m})} \end{array} $ | (27) |
其中i, j=1, 2, …, N.
式(26)等号右边的卷积式可表示为
| $ \begin{array}{*{20}{c}} {\left( {{d_2}\delta (t) + \sum\limits_{s = 1}^{NF} {{c_{2s}}} {{\rm{e}}^{{a_{2s}}t}}} \right){\mathit{\boldsymbol{E}}_0}\left( {t - \frac{z}{{{v_z}}}} \right) = }\\ {{d_2}\mathit{\boldsymbol{E}}_0^{n + 1 - (k - 0.5)\Delta z/{v_z}/\Delta t} + \sum\limits_{m = 0}^n {\mathit{\boldsymbol{E}}_0^{n + 1 - m - (k - 0.5)\Delta z/{v_z}/\Delta t}} \times }\\ {\sum\limits_{s = 1}^{NF} {\frac{{{c_{2s}}}}{{{a_{2s}}}}} ({{\rm{e}}^{{a_{2s}}(m + 1)\Delta t}} - {{\rm{e}}^{{a_{2s}}m\Delta t}})} \end{array} $ | (28) |
根据式(26)~式(28)可得传输线沿线各点的电流为
| $ \begin{array}{l} \mathit{\boldsymbol{I}}_k^{n + 1.5} = \mathit{\boldsymbol{I}}_k^{n + 0.5} - \frac{{\Delta z}}{{\Delta t}}{\mathit{\boldsymbol{F}}^{ - 1}}\left[ {\mathit{\boldsymbol{\psi }}_i^n - (\mathit{\boldsymbol{M}}_{k + 1}^{n + 1} - \mathit{\boldsymbol{M}}_k^{n + 1}) + } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {d_2}\Delta z\mathit{\boldsymbol{E}}_0^{n + 1 - (k - 0.5)\Delta z/\Delta t/{v_z}} + \Delta z\sum\limits_{s = 1}^{NF} {\mathit{\boldsymbol{f}}_{3s}^n} } \right] \end{array} $ | (29) |
其中:
因为m从0开始,n从1开始,所以f3s初值为
式(11)~式(29)中,Δz和Δt分别为空间离散步长和时间离散步长.为了确保算法稳定,必须满足Δt≤Δz/v的条件,取等号时Δt定义为最佳时间步长,其中v可取为光速.
5 算法验证及讨论 5.1 架空传输线系统受到外界电磁场辐照设架空单导体传输线(STL, single transmission line)长l=20 m,半径r=1.5 mm,架空高度h=0.8 m,首端负载RS=20 Ω,末端端接频变负载,如图 2所示,其中信号返回路径为大地.土壤电导率σg=0.001 S/m,相对介电常数εr=10.平面波入射,瞬态电场E0(t)=1.05(e-4×106t-e-4. 76×108t)V/m,入射波极化角θE=
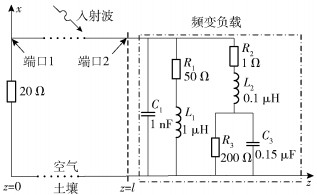
|
图 2 端接频变负载单导体传输线示意图 |
应用戴维南等效方法[7-8]计算得到频变负载端感应电压信号如图 3(a)所示,图中括号内的数值分别表示感应信号延迟时间和感应信号到达峰值的时间.应用本文算法计算得到传输线纯电阻端和频变负载端感应电压如图 3(b)所示,其中大地阻抗的拟合阶数NF=6,频变负载拟合阶数NF=12.

|
图 3 端接频变负载单导体传输线感应信号 |
从图 3可以看出,仿真得到末端负载处感应电压波形延迟时间是t=0.047 16 μs.线长l=20 m, 入射场俯仰角为θp=π/4, 根据Paul[9], 理论计算可得波形延迟时间为t =(l/c)cos(π/2-θp)≈0.047 14 μs.从延迟时间角度即可判断,仿真结果与理论分析结果吻合较好,能够验证仿真计算的正确性.应用本文算法可以得到传输线上任意一点处的电压、电流信号,且适用于双端都端接频变负载的情况,而戴维南方法只能用于单端端接频变负载的情况,且不能获取沿线任意点处感应信号.
5.2 多导体传输线系统电磁耦合实验某长度为l=1 m的三导体传输线,其中2根为信号线,一根为信号回路,端接负载如图 4所示.该多导体传输线受到集总电压源的激励,激励信号分别为梯形脉冲和双指数脉冲,其中梯形脉冲的上升沿、下降沿时间及脉冲宽度都为10 ns,双指数脉冲表达式为E0(t)=1.05(e-4×106t-e-4.76×108t)V/m.应用本文算法(其中频变负载拟合阶数NF=12)和状态变量法对该传输线进行计算,得到频变负载端感应电压信号波形,如图 5所示.
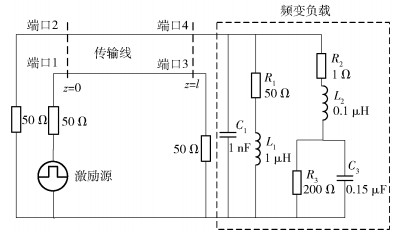
|
图 4 端接频变负载的理想多导体传输线示意图 |
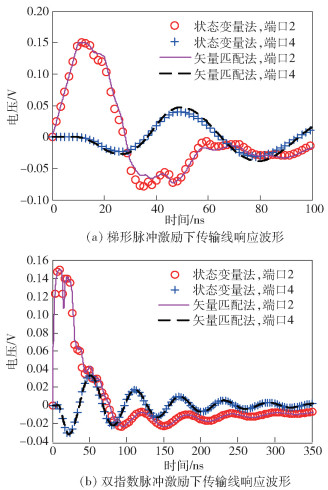
|
图 5 多导体传输线响应波形 |
从图 5可以看出,本文算法和状态变量法计算结果吻合很好,可验证本文算法的正确性.应用本文算法时,对于频变负载的处理,只需应用矢量匹配法对其拟合,得到一系列极点、留数及常数项,再进行编程计算即可.然而,应用状态变量法[7, 11]时,对于图 4所示不太复杂的频变负载电路,列写状态方程就已经非常复杂,如果电路形式更加复杂,则状态方程就非常不方便列出.因此本文算法在复杂频变负载电磁干扰建模分析方面是很有优势的.
通常频变负载并没有具体的电路模型,如电机绕组、非线性电阻等,这种情况下则可通过矢量网络分析仪或阻抗分析仪测量得到频变负载的导纳或阻抗参数,然后通过矢量匹配法拟合,得到一系列极点、留数和常数项,通过本文算法建立系统的数值模型,即可直接计算得到频变负载端在电磁干扰下的感应信号,不必再转换成电路形式,建模得以简化,计算非常方便.
6 结束语提出了一种用于求解端接频变负载传输线系统的电磁脉冲响应数值算法,应用分段线性递归卷积技术以简化时域计算过程,提高计算效率.通过与戴维南等效电路方法和状态变量法进行比较,验证了所提算法的正确性.与现有方法相比,本文算法较方便建立整个频变系统的数值模型,对于复杂传输线系统电磁脉冲响应计算具有较高的应用和参考价值.
| [1] |
Sinha R, Son H. Comments on dual-band design theory for dual transmission-line transformer[J]. IEEE Microwave and Wireless Components Letters, 2018, 28(12): 1155-1157. DOI:10.1109/LMWC.2018.2869295 |
| [2] |
Ryu Y, Park B R, Han K J. Estimation of high-frequency parameters of AC machine from transmission line model[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4. |
| [3] |
Olsen R G, Tarditi A G. EMP coupling to astraight conductor above ground:transmission line formulation based on electromagnetic reciprocity[J]. IEEE Transactions on Electromagnetic Compatibility, 2019, 61(3): 919-927. DOI:10.1109/TEMC.2018.2838080 |
| [4] |
Li Xue, Zhang Xiong, Wu Lei, et al. Transmission line overload risk assessment for power systems with wind and load-power generation correlation[J]. IEEE Transacions on Smart Grid, 2017, 6(3): 1233-1242. |
| [5] |
吴振军, 王丽芳, 廖承林. 分析端接频变负载的多导体传输线FDTD新方法[J]. 物理学报, 2009, 58(9): 6146-6151. Wu Zhenjun, Wang Lifang, Liao Chenglin. A novel FDTD method for multi-conductor transmission lines terminating in frequency-dependent loads[J]. Acta Physica Sinica, 2009, 58(9): 6146-6151. DOI:10.3321/j.issn:1000-3290.2009.09.043 |
| [6] |
Huangfu Youpeng, Di Rienzo L, Wang Shuhong. Frequency-dependent multi-conductortransmission line model for shielded power cables considering geometrical dissymmetry[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-4. DOI:10.1109/TMAG.2018.2800463 |
| [7] |
杨雨川, 盛定仪, 谭吉春. 配电线路-变压器系统对强电磁脉冲的电压响应[J]. 高电压技术, 2008, 34(6): 1168-1172. Yang Yuchuan, Sheng Dingyi, Tan Jichun. Induced voltage response characteristic of power-line transformer system against electromagnetic pulse[J]. High Voltage Engineering, 2008, 34(6): 1168-1172. |
| [8] |
潘晓东, 魏光辉, 卢新福, 等. 电磁注入等效替代辐照理论模型及实现技术[J]. 高电压技术, 2012, 38(9): 2293-2301. Pan Xiaodong, Wei Guanghui, Lu Xinfu, et al. Theoretical model and implementation technique of using injection as a substitute for radiation[J]. High Voltage Engineering, 2012, 38(9): 2293-2301. |
| [9] |
Paul C R. Analysis of multiconductor transmission lines[M]. NewYork: Wiley, 2007: 1-200.
|
| [10] |
Liu Xin, Cui Xiang, Qi Lei. Time-domain finite-element method for the transient response of multiconductor transmission lines excited by an electromagnetic field[J]. IEEE Transactions on Electromagnetic Compatibility, 2011, 53(2): 462-474. DOI:10.1109/TEMC.2010.2083653 |
| [11] |
Watanabe Y, Igarashi H. Accelerated FDTD analysis of antennas loaded by electric circuits[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(2): 958-963. DOI:10.1109/TAP.2011.2173148 |
| [12] |
Xia Fen, Chu Qingxin, Kong Yongdan, et al. The ADI-FDTD method including lumped networks using piecewise linear recursive convolution technique[J]. Progress in Electromagnetics Research M, 2013, 30(3): 67-77. DOI:10.2528/PIERM13012816 |
| [13] |
Gustavsen B, Semlyen A. Rational approximation of frequency domain responses by vector fitting[J]. IEEE Transactions on Power Delivery, 1999, 14(3): 1052-1061. DOI:10.1109/61.772353 |
| [14] |
Annakkage U D, Nair N K C, Liang Yuefeng, et al. Dynamic system equivalents:a survey of available techniques[J]. IEEE Transactions on Power Delivery, 2012, 27(1): 411-420. DOI:10.1109/TPWRD.2011.2167351 |


