提出了一种鲁棒网络流量分类及新类型的发现算法.网络流量一般为高维数据,且在网络流量收集过程中易受到网络波动或网络攻击的影响,为此,在堆栈自编码器的基础上,基于互相关熵理论提出了一种新的网络模型进行数据的特征提取,通过基于阈值的主动学习分类算法进行分类,达到识别新应用类型的目的.对比实验结果表明,所提算法中分类算法的准确度可达到91.08%,对新应用类型的识别度可达到98.8%.
A robust network traffic classification and new type discovery algorithm is proposed by this paper, which is based on sparse autoencoder to extract feature features and classify based on threshold-based active learning classification algorithm. In addition, to achieve the purpose of identifying new application types, the excellent performance of the proposed algorithm through comparative experiments is verified. Among them, the accuracy of the classification algorithm can reach 91.08%; the recognition of new application types can reach 98.8%.
近年来,随着互联网行业的高速增长与进步、通信技术的快速发展以及移动网络和智能手机的广泛普及,致使网络环境中网络流量的数量和类型都在不断地增长,这就需要提出新的网络流量分类方法,从而获得更准确的分类结果,满足新时代运营商对网络管理的新需求.
国内外学者对网络流量分类做了大量的相关研究,总体上网络流量分类可分为基于端口号、基于深度包检测[1]、基于行为模式以及基于机器学习4种类型[2].但是它们都会存在不同的问题,如不断变化的端口号、深度包检测的高复杂度以及加密应用等都无法满足高分类精度的要求.虽然机器学习可以通过统计信息明显地提高分类的准确度,但是无法识别网络中出现的新的网络流量类型.所以,笔者提出了一种新的网络分类算法,该算法在更准确地分类各业务流量的基础上还能识别出新应用产生的流量.
1 网络流量分类以及新应用发现模型通过基于相关熵的鲁棒性深度学习算法与主动学习[3]算法相结合,笔者提出一种新的鲁棒网络流量分类及新应用类型发现算法[4].
采用的Moore数据集是由Moore等收集的牛津大学的全双工网络流量,且每一个数据样本都是249维.由于维度较高计算难度大,且会有网络波动或网络攻击造成的噪声点,因此首先通过(CSAE, correntropy induced loss function based sparse atuoencoder)[5]来进行去噪处理及特征提取.
其次,由于网络应用发展迅速,为了满足新类型检测的环境,所以通过基于阈值的主动学习的思想进行流量分类以及识别出未知的流量类型.
最后,需要在识别的可能是新类型的异常点集合中进行新应用类型发现操作,这将通过(DBSCAN, density-based spatial clustering of applications with noise)算法来实现,当提取出其中新的应用类型后再去更新分类模型.模型结构如图 1所示.
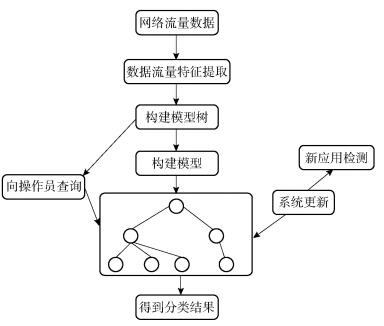
|
图 1 流量分类模型 |
由于Moore数据集维度较大,直接进行计算性能较差,因此需要进行特征提取.笔者选择自编码器进行特征提取,主要是隐藏层节点个数少于输入节点.
自编码器的目的是求函数:
| $ {h_{w,b}}(x) \approx x $ | (1) |
通过不断地减小输入和输出之间的误差,也就是不断地让隐藏层学习到更多输入层的信息,这样就完成了特征提取.
一般的自编码器都是使用均方误差(MSE, mean square error)作为损失函数,损失函数表达式为
| $ {J_{{\rm{ cost }}}} = {J_{{\rm{ MSE }}}}(\theta ) + {J_{{\rm{ weight }}}}(\theta ) + {J_{{\rm{ sparse }}}}(\theta ) $ | (2) |
其中:JMSE(θ)为损失函数,Jweight(θ)为权重,Jsparse(θ)为稀释项, θ为优化参数.
近年来,由于在信息理论学习的研究及核方法的基本思想[6]上Principe教授取得了很大的进步,因此互相关熵的概念应用而生,它是由基于随机过程的相关函数的定义推广而得出的广义相关函数.互相关熵是定义非线性信号映射到内核空间中的相似度度量.给定2个随机变量X和Y,互相关熵定义为
| $ V(X,Y) = E[\langle \varPhi (X),\varPhi (Y)\rangle ] = E[{\kappa _\sigma }(X,Y)] $ | (3) |
其中:kσ为具有核大小(或带宽)参数σ的径向核函数;Φ(·)为由kσ引入的非线性映射,其将数据从输入空间转换到高维再生核希尔伯特空间(RKHS, reproducing kernel Hilbert space)上;E为经验样本的均值(或样本均值)算子, 〈, 〉表示内积.给出2个样本,X=RM×N, Y=RM×N, X=[x1, x2, …, xN], Y=[y1, y2, …, yN], M是样本的维数,N是样本的个数,则经验相关熵可以表示为
| $ \hat V(X,Y) = \frac{1}{N}\sum\limits_{i = 1}^N {{\kappa _\sigma }} ({x_i},{y_i}) $ | (4) |
核方法是机器学习里强大而有效的工具,在互相关熵中,最受欢迎的核是高斯核,表示为
| $ {\kappa _\sigma }({x_i},{y_i}) = {\rm{exp}}\left( { - \frac{{{{\left\| {{\kern 1pt} {x_i} - {y_i}{\kern 1pt} } \right\|}^2}}}{{2{\sigma ^2}}}} \right) $ | (5) |
其中‖·‖为欧几里得范数.
文中互相关熵默认的内核函数是高斯核.在泛函分析的观点中,内核的大小决定了内积,即相似性度量在RKHS.如果内核太大,那么所有的数据将在RKHS下类似(内积都接近1),系统变成了线性回归.如果内核太小,所有的数据看起来都不一样(内积接近0),系统不能对落在训练点之间的看不见的样本进行推理.
根据互相关熵的定义,可以很容易地推导出基于互相关熵的损失函数Closs.对于分类任务而言,其目标是最大限度地提高分类器的输出样本X和标签样本Y之间的相似度,则Closs定义为
| $ {C_{{\rm{loss}}}}(X,Y) = \beta [1 - E({k_\sigma }(X,Y))] $ | (6) |
其中
| $ \beta = {\left[ {1 - {\rm{exp}}\left( { - \frac{1}{{2{\sigma ^2}}}} \right)} \right]^{ - 1}} $ | (7) |
β是用于保证Closs(0)=1的正比例常量.类似的,分类器的输出样本X和标签样本Y之间的经验C-loss可以定义为
| $ {C_{{\rm{ loss }}}}(X,Y) = \beta \left[ {1 - \frac{1}{N}\sum\limits_{i = 1}^N {({\kappa _\sigma }(} {x_i},{y_i}))} \right] $ | (8) |
图 2示出了Closs的曲线和导数曲线.其中,图 2(a)表示随着误差τ的增加,具有不同核大小σ函数值的Closs变化;图 2(b)表示具有不同核大小σ Closs函数的导数.为了更好地对比,图 2(b)中示出MSE的导数曲线,这是一个线性函数.由图可知,当使用误差较大的MSE时,导数将是巨大的,这意味着模型的权重会受到异常值或脉冲噪声的严重影响.相反,Closs在误差很大时导数很小,从而可以降低异常值的负面影响.因此,在数据含有异常值时,采用Closs代替MSE能在实际应用中有更好地表现.
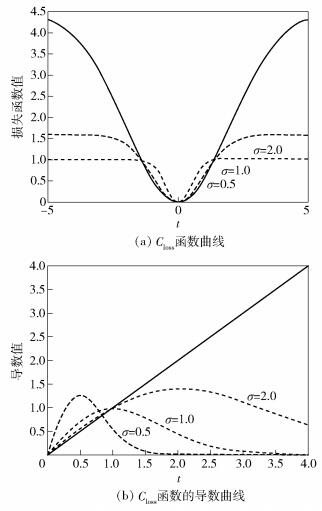
|
图 2 参数变换图 |
由于MSE对于异常值等非高斯噪声不够敏感,鲁棒性较差,而基于互相关熵的损失函数Closs对异常值具有更好的抗干扰能力,对原始数据也具有更稀疏的表示,因此可利用Closs来替代MSE损失函数建立一个高效且可靠的代价函数.而且,原始自编码算法的稀疏惩罚项也可以由基于Closs的稀疏惩罚项取代从而实现更好的性能.因此,笔者提出以下代价函数来训练SAE:
| $ {J_{{\rm{CASE\_cost }}}} = {J_{{\rm{ loss1}}}}(\theta ) + {J_{{\rm{ weight }}}}(\theta ) + {J_{{\rm{ loss2}}}}(\theta ) $ | (9) |
其中:Jloss1(θ)=Closs(X, Y)是基于Closs的重构损失,Jweight(θ)保持不变;Jloss2(θ)=Closs(θ, 0)是一个新的稀疏惩罚项.
通过最小化基于Closs的稀疏惩罚项,能够得到比原始数据更为稀疏的样本表示,而更为稀疏的样本表示意味着比原始数据更具有必要的信息和受异常值干扰更小.因此,改进的损失函数更具有鲁棒性.
2.2 基于阈值的主动学习分类算法在网络流量分类的研究中有许多分类算法,笔者之所以采用基于阈值的主动学习算法,一方面是因为通过阈值的方式进行分类计算速度较快;另一方面是因为通过该方法可以进行新类型发现.并且,主动学习的思想可以让模型在少量训练样本的前提下,同样可以拥有较好性能.
主动学习方法中通常需要一个学习引擎和一个选择引擎.
1) 学习引擎
对于学习引擎而言就是一个初始化的分类器,通过选择指定的算法对已经标签的数据进行学习和训练,得到最初的分类器模型.而且,在不断学习的过程中,该分类模型可以不断地提升准确率.
2) 选择引擎
由于选择出来的样本是未知类型的样本,所以需要交给人类专家进行样本类型的标注,然后再将其加入到对应的训练集中.在样本池中不断地重复选择信息量最大的样本这一过程,分类器的模型也在不断地提升着自己的准确度.
主动学习中最为主要的一点就是怎样在样本池中选择出来信息量最大的一个样本,因此选了基于专家委员会(QBC, query by committee)算法来进行样本的选择. 图 3为基于QBC的样本选择算法的主动学习过程.
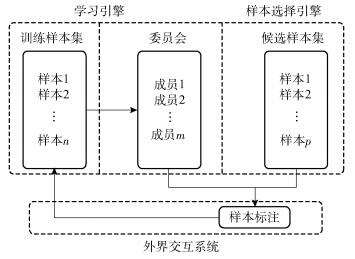
|
图 3 基于QBC的样本选择算法的主动学习过程 |
按照QBC样本选择算法,初始的分类模型会构造出多个分类模型来组成委员会,以此来对异常流量进行投票,然后度量委员会对各待检测流量样本的投票差异,将投票最不一致的流量样本选择出来,再向系统操作人员查询(Query)明确类型后,通过该样本类型去除分类错误的分支.
在明确主动学习算法的思想以及网络流量分类方法后,该框架核心由以下3部分组成.
① 一个基于相似度阈值的分类器,它可以决定一个新的样本是属于现有的分类器中某一类型,还是一个新的应用类型.
② 一个主动学习算法,它维护着这些分类器集合,当人类的反馈可用时,这个反馈就会剪枝操作.
③ 一个新的应用类型检测算法,该算法能适用于未知流量,以确定在未知流量中是否有样本子集代表一个新的应用类型.
分类器间对某一流量样本产生分歧的评判通过各分类器赋予该流量的类型标签(Label)的熵(Entropy)来量化.
令Committee中第jth个分类器赋予流量x的Label为y(j)(x),系统可以建立一个分类器委员会投票的直方图,来计算LabelY(x)的熵.
则共有M个成员的Committee中Label分布为
| $ p(Y(x) = l) = \sum\limits_{j = 1}^M \delta (l,{y^{(j)}}(x)) $ | (10) |
其中:l为Y(x)对应的样本,δ为Kronecker delta.则x的Shannon Entropy为
| $ H(Y(x)) = \sum\limits_{i = 0}^C - p(Y(x) = i){\rm{lg}}p(Y(x) = i) $ | (11) |
其中C为样本类型集合.
选择查询的流量对象为
| $ {x_{{\rm{ query }}}} = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{max}}}\limits_x H(Y(x)) $ | (12) |
通过查询得到的样本x去进行剪枝,然后修正该模型.
2.3 新应用发现算法在基于相似度阈值的主动学习分类过程中,当分类器模型在对待检测流量进行分类的时候,如果分类模型判断该流量可能为新类型产生的流量时,就将其加入到异常点集合中,但是无法确定异常点集合中有多少类新的网络流量,则需要选取不需要预先设定种类个数的聚类算法,故采用DBSCAN聚类算法来进行新类型发现.
由于传统DBSCAN算法使用的是欧氏距离计算对象间的差异大小,导致对高维数据聚类效果不理想.然而, 在网络流量研究中使用广泛的数据集的特征维度普遍较高.因此,结合互相关熵理论,针对网络流量数据集的高维特性,在衡量对象之间的差异性方面对传统的DBSCAN聚类算法加以改进.因为在算法实际运行时对于网络流量特征这样的高维数据集,各属性取值在高维空间上更加随机,对象之间的欧氏距离的差异比较不明显,而互相关熵的本质就是一种相似度度量方法,该度量方法是度量定义非线性信号映射到内核空间的,可以更好地体现样本之间的差异性.
网络流量特征空间中,对象X=[x1, x2, …, xN],Y=[y1, y2, …, yN].因此相关熵表达式为:
| $ {\hat V_\sigma }(X,Y) = \frac{1}{N}\sum\limits_{i = 1}^N {{k_\sigma }} ({x_i} - {y_i}) $ | (13) |
其中
| $ {k_\sigma }({x_i} - {y_i}) = {\rm{exp}}\left( { - \frac{{{{\left\| {{x_i} - {y_i}} \right\|}^2}}}{{2{\sigma ^2}}}} \right) $ | (14) |
按照互相关熵的概念,重新定义DBSCAN算法中给定对象的Eps领域为:以该对象为中心,与该对象的互相关熵值大于Eps的一个范围区域.
由于实际网络环境中的新应用流量类型以及数量往往呈爆炸性增长,检测到的未知流量中包含的新类型数量、分布密度是存在变化而不可预知的,因此需要根据未知流量数据集的特性来确定合适的聚类参数.
为了满足所研究环境下的情形,在Li等[7]对DBSCAN参数自适应的研究基础上进一步进行改进,以此来满足文中的场景,并且考虑预设了当异常点集合中未知流量数量达到某一固定值时就进行新类型发现操作.因此对参数Eps的计算加以改变为
| $ E{\rm{ps}} = k\ \overline {{\rm{entropy}}} $ | (15) |
其中:k为常数,Entropy为数据集样本间互相关熵的平均值. k的取值通过对已知类型的训练集数据进行多次聚类实验,根据聚类效果确定.另外重新定义核函数:
| $ K(u) = \left\{ {\begin{array}{*{20}{l}} {1,}&{|{u_i}| \ge 1}\\ {0,}&{|{u_i}| < 1} \end{array}} \right. $ | (16) |
则参数MinPts确定为
| $ {\rm{MinPts}} = \sum\limits_{i = 1}^n K \left( {\frac{{ {\rm{entropy}} (x,{x_i})}}{{Eps}}} \right) $ | (17) |
其中:x为数据集样本空间的中心点处的对象,Entropy(x, xi)为对象x与xi的互相关熵值.
3 仿真结果实验数据集均采用Moore数据集,由于需要进行多个对比实验,所以需要设置不同的数据集来满足不同的实验环境.
由于多个对比实验都用到了SAE和CSAE进行特征提取,通过实验以及文献[5]将网络结构设置为249-100-100-249.其中核心参数如表 1所示.
|
|
表 1 自编码器核心参数 |
为了验证模型对已知应用类型分类的效果,在通过CSAE算法进行数据特征提取的前提下,验证基于相似度阈值的分类方法的优势,因此采用了数据集DATA1进行验证,具体描述如表 2所示.该数据集将训练数据个数设置为1000用来初始化分类器,将测试数据个数设置为200来进行验证,结果如表 3所示.
|
|
表 2 数据集DATA1 |
|
|
表 3 不同相似度计算标准下分类准确率对比 |
由实验结果表明,在使用互相关熵计算相似度的情况下,准确率高于欧氏距离以及余弦相似度.
3.2 未知流量分类实验及分析为了反映不同的相似度计算标准下,基于相似度阈值的分类算法对未知流量的检测效果,用包含已知流量和未知流量的数据集进行未知流量检测的实验.因此选用数据集DATA2,如表 4所示,该数据集中只将类型WWW、MAIL及FTP-CONTROL的训练数据样本设置为1500,其余类型设置为0,以此来模拟新类型.
|
|
表 4 数据集DATA2 |
按照基于相似度阈值的主动学习分类算法,首先通过对训练数据进行学习,得到各自已知类型的阈值分类标准,然后将测试数据集打乱顺序后逐条进入系统,按照阈值分类标准进行分类判断和未知流量检测.使用互相关熵、欧氏距离[8]及余弦相似度[9]不同的相似度计算标准进行未知流量的检测实验,实验结果如表 5所示.由表 5可以明显地发现,通过互相关熵的相似度计算方式,不仅对未知流量的识别率高于其他2种方式,而且对流量的误判率也低于其他2种方式.
|
|
表 5 已知流量分类以及新类型发现结果 |
由于采用了CASE进行数据的特征提取,因此对比了在使用SAE以及未进行数据预处理的情况下的准确率.实验数据使用DATA1数据集,结果如表 6所示.
|
|
表 6 不同数据处理下分类准确率对比 |
由实验结果可知,通过CSAE来进行特征提取在分类算法上效果相比于SAE以及未进行特征提取的方法更加优异.
3.4 新类型发现实验及分析为了验证改进后的新类型发现算法的优势,通过对数据集DATA3(见表 7)进行验证,对于每一种类型都选取200个数据样本,然后将其放入异常点集合中作为新应用类型产生的流量,结果如表 8所示.
|
|
表 7 数据集DATA3 |
|
|
表 8 改进DBSCAN和传统DBSCAN算法对比 |
实验结果表明,改进的新应用发现算法相较于传统的算法效果更优.
4 结束语笔者提出了一种鲁棒流量分类及新应用类型发现算法,在流量分类的过程中主要是采用CSAE来进行数据的特征提取,然后通过主动学习的思想来进行流量分类,最终通过改进的DBSCAN聚类算法进行新类型发现.由仿真实验可以看到,通过CSAE进行数据降维后再进行分类的准确度较好,而且新类型发现准确度也较高,因此所提出的鲁棒网络流量分类算法具有很好的实际意义.
| [1] |
张鹰, 邱永红. 海岸带地物特征的遥感信息提取方法[J]. 海洋预报, 2002(3): 14-21. Zhang Ying, Qiu Yonghong. Remote sensing information extraction method of coastal features[J]. Marine Forecasts, 2002(3): 14-21. |
| [2] |
陶筱娇, 王鑫. 基于深度学习算法的图像分类方法[J]. 微型电脑应用, 2019, 35(3): 40-43. Tao Xiaojiao, Wang Xin. Image classification method based on deep learning algorithms[J]. Microcomputer Applications, 2019, 35(3): 40-43. |
| [3] |
Evan Kriminger, Tory Cobb J, Jose C Principe. Online active learning for automatic target recognition[J]. IEEE Journal of Oceanic Engineering, 2015, 40(3): 583-591. |
| [4] |
Zhang Jun, Chen Xiao, Xiang Yang. Robust network traffic classification[J]. IEEE/ACM Transaction on Networking, 2015, 82(5): 1257-1270. |
| [5] |
Chen Liangjun, Qu Hua, Zhao Jihong. Efficient and robust deep learning with correntropy induced loss function[J]. Neural Computing and Application, 2016, 27(4): 1019-1031. |
| [6] |
Liu Weifeng, Puskal P Pokharel, Jose C. A localized similarity measure in neuralnetworks, 2006. IJCNN 06. International Joint Conference on, 2007, 55(4): 5286-5298.
|
| [7] |
Li Zonglin, Luo Ke. Research on adaptive parameters determination in DBSCAN algorithm[J]. Computer Engineering and Applications, 2016, 52(3): 70-73. |
| [8] |
Yin Xiaoqi, Jindal Abhishek, Bruno. A control-theoretic approach for dynamic adaptive video streaming over HTTP[J]. Acm Sigcomm Computer Communication Review, 2015, 45(4): 325-338. |
| [9] |
Pu Wang, ShihChun Lin, Min Luo. A framework for QoS-aware traffic classification using semi-supervised machine learning in SDNs[C]//IEEE International Conference on Services Computing. IEEE, 2016, 36(4): 1155-1167. https://www.researchgate.net/publication/305283745_A_Framework_for_QoS-aware_Traffic_Classification_Using_Semi-supervised_Machine_Learning_in_SDNs
|



