2. 机械工业仪器仪表综合技术经济研究所, 北京 100055
超密集网络设备数目庞大导致缓存分配算法复杂度极高,频繁地缓存和删除同样的内容导致的系统不稳定,为此,提出了基于平均场博弈(MFG)的分布式缓存分配算法和基于李雅普诺夫漂移加惩罚(DPP)方法的分布式删除分配算法.MFG方法使缓存分配算法的复杂度与基站数目无关.DPP方法将具有时间相关性的删除分配问题解耦成为每个时刻的问题,并求解得到了兼顾系统稳定性和网络开销优化的删除分配策略.仿真结果表明,MFG方法能够使网络最优控制策略快速收敛,并且在超密集场景下得到明显低于基本缓存分配方法的网络开销;李雅普诺夫DPP方法能够实现兼顾网络开销优化的网络缓存和删除稳定性.
2. Instrument Technology and Economy Institute, Beijing 100055, China
A distributed caching allocation algorithm based on mean-field game (MFG) and a distributed deleting allocation algorithm based on Lyapunov drift-plus-penalty (DPP) method were proposed to solve the problem of caching allocation algorithms' extremely high complexity caused by lots of devices in ultra-dense network and the problem of system instability caused by caching and deleting same content frequently. The caching allocation algorithm's complexity independent of the number of base stations is made by MFG. The time-correlated deleting allocation problem into problems each time slot is decoupled by DPP. Thereafter the deleting allocation policy for the tradeoff between system stability and minimizing network cost gets solved. Simulation shows that MFG can both make the network optimal control strategy converge quickly and save network cost obviously compared to baseline caching allocation method under ultra-dense scenario. Lyapunov DPP method can ensure network caching and deleting stability while minimizing network cost.
边缘缓存网络中,当一个基站在制定缓存分配策略时,既要考虑存储受限的内容重叠,又要考虑容量受限的链路干扰问题.在基站数目庞大的超密集网络中势必造成基站间信息的高度耦合.一方面,“内容重叠”[1]需要涉及全部其他基站的缓存分配策略;另一方面,在计算下行链路干扰时考虑全部其他基站的传输功率和信道增益.此外,频繁地缓存和删除同一内容导致的系统不稳定也是一个容易被忽视的问题.因此,兼顾系统稳定性的联合缓存和删除分配机制有待进一步研究.
近年来,平均场(MF, mean-field)理论在超密集网络的研究中得到了广泛的关注[2-3].基于MF理论,可以通过统计平均效果来研究大量相互作用的个体的行为[4]. MF理论可以将多个个体的问题转化为单一个体的问题,故可以在设备数目庞大的超密集网络中大幅降低网络优化的复杂度. Hamidouche等[5]研究了基于平均场博弈(MFG, mean-field game)方法的超密集网络分布式缓存分配机制,虽然其运用MFG方法对内容重叠实现了低复杂度的计算,但在干扰的计算上没有做任何处理. Kim等[6]采用MFG方法对内容重叠实现了低复杂度的计算,但在干扰的计算方面,采用的是随机几何方法,仅考虑了干扰的空间动态特性,忽视了干扰的时间动态特性,故不能很好地适应信道状态信息(CSI, channel state information)随时间的演化.所以,对于MF理论在内容重叠计算和干扰计算上的应用的结合有待实现.
基于李雅普诺夫理论的漂移加惩罚(DPP, drift-plus-penalty)方法可以很好地解决边缘缓存网络的系统稳定性问题[7-8]. DPP方法可以将一个优化一段时间的平均值的随机优化问题简化为多个优化每时刻瞬时值的确定性优化问题. Samarakoon等[9]采用DPP方法依照队列状态信息进行用户调度,实现了系统的队列稳定性.张琪[10]针对与稳定性相关的缓存控制和接入控制变量分别构造了虚拟队列,并依照虚拟队列进行缓存控制和接入控制,最终实现了系统稳定性.
针对上述问题,笔者提出了基于MFG的分布式缓存分配策略和基于DPP方法的分布式删除分配策略.每个基站通过独立地控制其缓存和删除分配策略,实现预定义的开销函数的长时间平均(LRA, long run average)值的最小化.
1 系统模型和问题构造 1.1 系统模型考虑一个超密集网络,系统包含K个基站,集合为
| $ {\rm{d}}{Q_{k,j}}(t) = [{e_{k,j}}(t) - {p_{k,j}}(t)]{\rm{d}}t $ | (1) |
假定用户只接入与之距离小于R的基站,在与之距离小于R的基站集合中,用户选择对其当前请求文件内容缓存最多的基站.当没有基站缓存了用户当前的请求文件时,用户选择距离最近的基站接入.令xk, j(t)为基站k附近文件j的流行度[6],其动态变化服从均值为μj、变速参数为r的奥恩斯坦-乌伦贝克过程:
| $ {\rm{d}}{x_{k,j}}(t) = r({\mu _j} - {x_{k,j}}(t)){\rm{d}}t + \eta {\rm{d}}{W_{k,j}}(t) $ | (2) |
其中:η>0为常数,Wk, j(t)为维纳过程.
系统CSI[5]的演化过程为
| $ {\rm{d}}{h_k}(t) = G(t,{h_k}(t)){\rm{d}}t + \zeta {\rm{d}}{z_k}(t) $ | (3) |
其中:G(t, hk(t))考虑了路径损耗和阴影,ζdzk(t)包含快衰落和信道不确定性.假定所有基站以等功率P向用户传输信息,基站k到其服务用户的下行链路干扰为
| $ {I_k}(t) = \sum\limits_{{k^\prime } \in \mathscr{K}\backslash \{ k\} } {P|{h_{{k^\prime }}}(t){|^2}} $ | (4) |
则系统下行链路速率为
| $ {R_k}(t) = W{\kern 1pt} {\kern 1pt} {\rm{lg}}\left( {1 + \frac{{P|{h_k}(t){|^2}}}{{\sum\limits_{{k^\prime } \in \mathscr{K}\backslash \{ k\} } P |{h_{{k^\prime }}}(t){|^2} + {\sigma ^2}}}} \right) $ | (5) |
其中σ2为高斯白噪声功率.
在边缘缓存网络中瞬时开销函数综合考虑了网络回程链路开销、基站的剩余存储空间、下行链路速率以及不同基站间的缓存内容重叠.其中回程链路缓存开销[5]为
| $ {\phi _{k,j}}({p_{k,j}}(t)) = - {\rm{lg}}\left( {\frac{{{B_j}(t) - {p_{k,j}}(t)}}{{{B_j}(t)}}} \right) $ | (6) |
由于缓存的文件占据基站的存储空间,这会导致处理时延以及文件查询时延[11],故定义与缓存大小成正比(不妨设比例系数为γ)的文件存储开销:
| $ {\psi _{k,j}}({Q_{k,j}}(t)) = \gamma [{C_j} - {Q_{k,j}}(t)]/{C_j} $ | (7) |
定义内容重叠函数:
| $ I_{k,j}^r({\mathit{\boldsymbol{P}}_{ - k,j}}(t)) = \frac{1}{{{C_j}{L_j}K}}\sum\limits_{{k^\prime } \in {\mathscr{K}^\prime }\backslash \{ k\} } {{p_{{k^\prime },j}}(t)} $ | (8) |
该函数用于描述一个文件在所有基站中的重复缓存程度.全局瞬时开销函数为
| $ \begin{array}{l} {J_{k,j}}(t) = \frac{{{\phi _{k,j}}({p_{k,j}}(t))[1 + I_{k,j}^r({\mathit{\boldsymbol{P}}_{ - k,j}}(t))]}}{{{R_k}(t){x_{k,j}}(t)}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _{k,j}}({Q_{k,j}}(t)) \end{array} $ | (9) |
每个基站k的目标是在保证系统稳定性的条件下,通过对每个文件j控制缓存分配pk j(t)和删除分配ek, j(t),最小化对该文件的LRA开销.优化问题可以写成
| $ {\mathscr{P}:\mathop {{\rm{min}}}\limits_{({p_{k,j}},{e_{k,j}})} \mathop {{\rm{lim}}}\limits_{t \to \infty } \frac{1}{t}\int_0^t {{J_{k,j}}} (\tau ){\rm{d}}\tau } $ | (10a) |
| $ {{\mathop{\rm s}\nolimits} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm t}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{式 }}(1)\backsim 式(3)} $ | (10b) |
| $ {{p_{k,j}}(t) \in [0,{B_j}(t)]} $ | (10c) |
| $ {{e_{k,j}}(t) \in [0,{E^{{\rm{max}}}}]} $ | (10d) |
| $ {\mathop {{\rm{lim}}}\limits_{t \to \infty } \frac{1}{t}\int_0^t {{e_{k,j}}} (\tau ){\rm{d}}\tau < {\gamma _e}} $ | (10e) |
其中:约束式(10e)表示系统的稳定性,即一个基站对于同一个文件不得频繁地缓存和删除;γe表示LRA删除的上界.虽然式(10e)本身和缓存速率无关,但只要删除不频繁,由约束式(1)可得缓存频率自然会随之降低.
考虑到缓存分配受制于服务中心到基站的回程容量和基站自身的开销最小化目标,其速度较慢,既需要通过每时每刻的积累才能实现对文件的缓存,也需要随着约束式(1)~式(3)随时调整.而删除分配是基站内部的自我管理行为,且开销几乎为0,所以不受任何限制,速度非常快(即Emax非常大,以至于ek, j(t)∈[0, Emax]的限制可以忽略不计),并且删除需要相对于缓存有一定的迟滞,即缓存后一段时间再进行删除,以防删除过早导致的未来短时间内所需文件的丢失.故需要在缓存和删除分配之间进行时间尺度分离,缓存分配是时刻变化的,为短时优化,而删除分配每隔时间T进行一次即可,为长时优化,每次制定的删除分配重新定义为
由前面的重定义删除分配可知,只在t=T, 2T, …时刻进行删除,故每次短时优化的时间段内没有删除分配,式(1)改写为式(11c).
短时优化的目标是基站对每个文件制定缓存策略.短时优化问题为(不妨设短时优化的时间段为[0, T])
| $ {{\mathscr{P}_{\rm{s}}}:\mathop {{\rm{min}}}\limits_{{p_{k,j}}} {\varGamma _{k,j}}(0)} $ | (11a) |
| $ {{\mathop{\rm s}\nolimits} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{式 }}(2),式(3)} $ | (11b) |
| $ {{\rm{d}}{Q_{k,j}}(t) = - {p_{k,j}}(t){\rm{d}}t} $ | (11c) |
| $ {{p_{k,j}}(t) \in [0,{B_j}(t)]} $ | (11d) |
其中Γk, j(t)表示[t, T]时间段内开销的积分:
| $ {\varGamma _{k,j}}(t) = \int_t^T {{J_{k,j}}} ({p_{k,j}}(\tau ),{\mathit{\boldsymbol{P}}_{ - k,j}}(\tau )){\rm{d}}\tau $ | (12) |
由于基站的状态随时间的动态演化由式(2)、式(3)和式(11c)所示,每个基站的缓存分配必须随之适应.因此,在时间动态下最小化LRA开销的问题可以建模为动态随机微分博弈[12](SDG, stochastic differential game)(一个文件一个博弈,且不同的文件相互独立).博弈的“局中人”(player, 博弈的要素之一)为基站,基站的状态为Sk, j(t)=[hk(t), Qk, j(t), xk, j(t)], ∀k∈
| $ \begin{array}{l} \begin{array}{*{20}{c}} {0 = \frac{{\partial {\varGamma _{k,j}}({h_k},{Q_{k,j}},{x_{k,j}},t)}}{{\partial t}} + }\\ {\mathop {{\rm{min}}}\limits_{{p_{k,j}}(t)} \left[ {{J_{k,j}}({p_{k,j}}(t),{\mathit{\boldsymbol{P}}_{ - k,j}}(t)) + } \right.}\\ {G(t,{h_k}(t))\frac{{\partial {\varGamma _{k,j}}}}{{\partial {h_k}}} - {p_{k,j}}(t)\frac{{\partial {\varGamma _{k,j}}}}{{\partial {Q_{k,j}}}} + }\\ {r({\mu _j} - {x_{k,j}}(t))\frac{{\partial {\varGamma _{k,j}}}}{{\partial {x_{k,j}}}} + } \end{array}\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\zeta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _{k,j}}}}{{\partial h_k^2}} + \frac{{{\eta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _{k,j}}}}{{\partial x_{k,j}^2}}} \right] \end{array} $ | (13) |
若式(13)对于全部基站有公共解,则问题
定义1 对于一个给定全部基站的缓存控制策略组合{p1, j*(t), …, pk, j*(t)},若对于任意基站k,任意可能的缓存控制策略组合{p1, j(t), …, pk j(t)}(其中,对于∀k∈
| $ \begin{array}{*{20}{c}} {\int_0^T {{J_{k,j}}} (p_{k,j}^*(\tau ),\mathit{\boldsymbol{P}}_{ - k,j}^*(\tau )){\rm{d}}\tau \le }\\ {\int_0^T {{J_{k,j}}} ({p_{k,j}}(\tau ),\mathit{\boldsymbol{P}}_{ - k,j}^*(\tau )){\rm{d}}\tau } \end{array} $ | (14) |
那么{p1, j*(t), …, pk, j*(t)}是纳什均衡.
由于定义时间动态的漂移函数式(13)中一阶导数的系数以及开销函数式(9)均具备平滑性,式(13)对于全部基站有唯一公共解[13]及其相应的唯一纳什均衡.然而,在K个HJB方程的交织系统的求解中,每个基站都需要考虑全部其他基站的缓存分配和信道增益,所以当基站数目K>2时,该方法有着极大的计算复杂度.然而,当K足够大,并且基站满足对于缓存控制策略的可交换性(同一时刻,不同的基站在相同的自身状态下控制策略相同)时,可以将该SDG转化为MFG,并通过迭代收敛至纳什均衡.
2.1 基于MFG的问题求解MF是所有“局中人”(基站)对状态(CSI、剩余缓存空间以及流行度)的分布密度,这里由mj(h, Qj, xj, t)表示,其定义为
| $ \begin{array}{*{20}{l}} {{m_j}(h,{Q_j},{x_j},t) = \mathop {{\rm{lim}}}\limits_{K \to \infty } \frac{1}{K}\sum\limits_{k \in K} \delta \{ {h_k}(t) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} h,{Q_{k,j}}(t) = {Q_j},{x_{k,j}}(t) = {x_j}\} } \end{array} $ | (15) |
MF由福克-普朗克-柯尔莫哥洛夫(FPK, Fokker-Planck-Kolmogorov)方程式(16)求得.
| $ \begin{array}{l} 0 = \frac{{\partial {m_j}}}{{\partial t}} + G(t,h)\frac{{\partial {m_j}}}{{\partial h}} - {p_j}(h,{Q_j},{x_j},t)\frac{{\partial {m_j}}}{{\partial {Q_j}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r({\mu _j} - {x_j})\frac{{\partial {m_j}}}{{\partial {x_j}}} - \frac{{{\zeta ^2}}}{2}\frac{{{\partial ^2}{m_j}}}{{\partial {h^2}}} - \frac{{{\eta ^2}}}{2}\frac{{{\partial ^2}{m_j}}}{{\partial x_j^2}} \end{array} $ | (16) |
注意,式(16)中的pj(h, Qj, xj, t)对应前面的可交换性的假设.求得了MF mj*(h, Qj, xj, t),干扰和内容重叠函数可由式(17)计算.
| $ \begin{array}{*{20}{c}} {{I_k}(t) = \sum\limits_{{k^\prime } \in \mathscr{K}\backslash \{ k\} } {P|{h_{{k^\prime }}}(t){|^2}} \approx \sum\limits_{{k^\prime } \in K} P |{h_{{k^\prime }}}(t){|^2} \approx }\\ {KP\int {{h^2}} m_j^*{\rm{d}}h{\rm{d}}{Q_j}{\rm{d}}{x_j} = I(m_j^*) = {I^*}(t)} \end{array} $ | (17a) |
| $ \begin{array}{*{20}{c}} {I_{k,j}^r({\mathit{\boldsymbol{P}}_{ - k,j}}(t)) = \frac{1}{{{C_j}{L_j}K}}\sum\limits_{{k^\prime } \in \mathscr{K}\backslash \left\{ k \right\}} {{p_{{k^\prime },j}}} (t) \approx }\\ {\frac{1}{{{C_j}{L_j}K}}\sum\limits_{{k^\prime } \in \mathscr{K}} {{p_{{k^\prime },j}}} (t) \approx }\\ {\frac{1}{{{C_j}{L_j}}}\int {{p_j}} (h,{Q_j},{x_j},t)m_j^*{\rm{d}}h{\rm{d}}{Q_j}{\rm{d}}{x_j} = }\\ {I_j^r(m_j^*) = I_j^{r*}(t)} \end{array} $ | (17b) |
此时基站已经不需要考虑其他基站的状态和缓存控制策略了,只需知道MF.此时式(12)可以改写为
| $ {\varGamma _j}(t) = \int_t^T {{J_j}} ({p_j}(h,{Q_j},{x_j},t),{I^*}(t),I_j^{r*}(t)){\rm{d}}\tau $ | (18) |
将式(18)代入式(13)得到MF-HJB方程:
| $ \begin{array}{*{20}{c}} {0 = \frac{{\partial {\varGamma _j}(h,{Q_j},{x_j},t)}}{{\partial t}} + }\\ {\mathop {{\rm{min}}}\limits_{p,(h,Q,x,x,t)} \left[ {{J_j}({p_j}(h,{Q_j},{x_j},t),{I^*}(t),I_j^{r*}(t)) + } \right.}\\ {G(t,h)\frac{{\partial {\varGamma _j}}}{{\partial h}} - {p_j}(h,{Q_j},{x_j},t)\frac{{\partial {\varGamma _j}}}{{\partial {Q_j}}} + }\\ {\left. {r({\mu _j} - {x_j})\frac{{\partial {\varGamma _j}}}{{\partial {x_j}}} + \frac{{{\zeta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _j}}}{{\partial {h^2}}} + \frac{{{\eta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _j}}}{{\partial x_i^2}}} \right]} \end{array} $ | (19) |
这是一个单独的HJB方程,式(13)中的耦合已经完全不存在了.通过逆向归纳法求解式(19)可以得到LRA开销的最优迹Γj*(h, Qj, xj, t),其对应的MF mj*(h, Qj, xj, t)则是通过正向归纳法求解式(16)的结果,这一对解[mj*(h, Qj, xj, t), Γj*(h, Qj, xj, t)]构成纳什均衡.定义pj*(h, Qj, xj, t)为由开销最优迹Γj*(h, Qj, xj, t)和MF分布mj*(h, Qj, xj, t)生成的达到纳什均衡的最优缓存控制策略.最优解pj*(h, Qj, xj, t)由命题1给出.
命题1 基站最优缓存控制策略为
| $ p_j^*(h,{Q_j},{x_j},t) = {B_j}(t) - \frac{{1 + I_j^{r*}(t)}}{{R(h,{I^*}(t)){x_j}\frac{{\partial {\varGamma _j}}}{{\partial {Q_j}}}}} $ | (20) |
其中Ijr*(t)、I*(t)和∂Γj/∂Qj分别是式(17)和式(19)的唯一解.其证明过程见附录.
考虑到求解FPK方程需要给定LRA开销的最优迹(HJB方程的解)对应的最优缓存控制策略,求解HJB方程需要给定MF(FPK方程的解),所以需要通过迭代求解这对耦合的方程.
2.2 HJB-FPK方程组的求解算法采用不动点论证法[15]求解耦合HJB-FPK方程组的收敛解.为了能够仿真求解偏微分方程,需要采用Δt→0的离散时间模拟连续时间,积分也用求和的方式代替,即
| $ \begin{array}{*{20}{l}} {\frac{{{h_{{\rm{max}}}}\Delta t}}{{{{(\Delta h)}^2}}} \le \frac{1}{2}}\\ {\frac{{{Q_{j{\rm{max}}}}\Delta t}}{{{{(\Delta {Q_j})}^2}}} \le \frac{1}{2}}\\ {\frac{{{x_{j{\rm{max}}}}\Delta t}}{{{{(\Delta {x_j})}^2}}} \le \frac{1}{2}} \end{array} $ | (21) |
| $ \begin{array}{*{20}{l}} {\frac{{{\rm{d}}f(x)}}{{{\rm{d}}x}} = \frac{{f(x) - f(x - \Delta x)}}{{\Delta x}}}\\ {\frac{{{\rm{d}}f(x)}}{{{\rm{d}}x}} = \frac{{f(x + \Delta x) - f(x)}}{{\Delta x}}}\\ {\frac{{{{\rm{d}}^2}f(x)}}{{{\rm{d}}{x^2}}} = \frac{{f(x + \Delta x) - 2f(x) - f(x - \Delta x)}}{{{{(\Delta x)}^2}}}} \end{array} $ | (22) |
对于算法实现,以下步骤为先决条件:
1) 通过式(22)离散化MF-HJB方程式(19)和MF-FPK方程式(16);
2) 通过式(22)离散化方程式(2)、式(3)和式(11c);
3) 为Δt、Δh、ΔQj和Δxj设定符合条件式(21)的值.
完成了上述准备工作,就可以通过算法1求解HJB-FPK方程组,并且基于算法1的解,每个基站可以通过算法2求解自己的最优控制策略和相应的最低开销函数.
算法1 不动点论证法求解HJB-FPK方程组
输入:短时优化时长T,收敛精度ε,pj0(h, Qj, xj, t),0时刻MF mji(h, Qj, xj, 0).
步骤1 求解式(16),解由mj0(h, Qj, xj, t)表示;
步骤2 i=1, d=1;
步骤3 将mji-1(h, Qj, xj, t)代入式(17)求得干扰和内容重叠函数,并代入式(19),在反向时间方向上求解MF-HJB方程,解由Γji(h, Qj, xj, t)表示;
步骤4 根据式(20)求解最优缓存控制策略,解由pji(h, Qj, xj, t)表示,其中
步骤5 将pji(h, Qj, xj, t)代入式(16),在正向时间方向上求解MF-FPK方程,解由mji(h, Qj, xj, t)表示;
步骤6 d=|mji(h, Qj, xj, t)-mji-1(h, Qj, xj, t)|, i=i+1;
步骤7 检查d,如果不满足条件d < ε,则返回步骤3,否则终止.
输出:纳什均衡mj(h, Qj, xj, t), Γj(h, Qj, xj, t).
算法2 一个基站的分布式缓存控制策略
输入:mj(h, Qj, xj, t), Qk, j(0), xk, j(0), hk(0),随机过程Wk, j, zk.
步骤1 将Wk, j, zk代入式(2)和式(3)求得xk, j(t), hk(t);
步骤2 Γk, j(t)=0, N=T/Δt, n=0;
步骤3 将pk j(nΔt)代入MF-HJB方程式(19) (先代入,暂不求解),代入式(11c)导出Qk, j((n+1)Δt);
步骤4 根据式(17)计算干扰I((n+1)Δt)和内容重叠函数Ijr((n+1)Δt),并代入MF-HJB方程式(19)求得Γk, j((n+1)Δt);
步骤5 将步骤4的解代入式(20)求得pk j((n+1)Δt),其中
步骤6 n=n+1;
步骤7 检查n,如果不满足条件n=N,则返回步骤3,否则终止.
输出:Γk, j(t), pk j(t).
3 长时优化问题:基于李雅普诺夫理论的删除分配长时优化的目标是基站对文件制定删除策略.考虑到长时优化问题每隔时间T进行一次,时间已经离散化(不妨设T=1,将时间归一化),以及第1节对删除策略的重定义,并且开销中只有存储开销和删除策略有关,则长时优化的子问题为
| $ {{\mathscr{P}_{\rm{s}}}:\mathop {{\rm{min}}}\limits_{{p_{k,j}}} {\varGamma _{k,j}}(0)} $ | (23a) |
| $ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {Q_{k,j}}(t + 1) = {Q_{k,j}}(t) + {{\hat e}_{k,j}}(t) - {{\hat p}_{k,j}}(t)} $ | (23b) |
| $ {{{\hat e}_{k,j}}(t) \in [0,{C_j} - {Q_{k,j}}(t)]} $ | (23c) |
| $ \mathop {{\rm{lim}}}\limits_{t \to \infty } \frac{1}{t}\sum\limits_{\tau = 0}^{t - 1} {{{\hat e}_{k,j}}} (\tau ) < {\gamma _e} $ | (23d) |
其中
由李雅普诺夫理论,构建虚拟队列:
| $ {\alpha _{k,j}}(t + 1) = {\rm{max}}[0,{\alpha _{k,j}}(t) + {\hat e_{k,j}}(t) - {\gamma _e}] $ | (24) |
李雅普诺夫函数为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta L(t) = L(t + 1) - L(t) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}[\alpha _{k,j}^2(t + 1) - \alpha _{k,j}^2(t)] \le \\ {\kern 1pt} {\kern 1pt} \frac{1}{2}{[{\alpha _{k,j}}(t) + {{\hat e}_{k,j}}(t) - {\gamma _e}]^2} - \alpha _{k,j}^2(t)] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}[\alpha _{k,j}^2(t) + {[{{\hat e}_{k,j}}(t) - {\gamma _e}]^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{\alpha _{k,j}}(t)[{{\hat e}_{k,j}}(t) - {\gamma _e}] - \alpha _{k,j}^2(t)] = \\ \frac{1}{2}{[{{\hat e}_{k,j}}(t) - {\gamma _e}]^2} + {\alpha _{k,j}}(t)[{{\hat e}_{k,j}}(t) - {\gamma _e}] \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} U + {\alpha _{k,j}}(t)[{{\hat e}_{k,j}}(t) - {\gamma _e}] \end{array} $ |
即
| $ \Delta L(t) \le U + {\alpha _{k,j}}(t)[{\hat e_{k,j}}(t) - {\gamma _e}] $ | (25) |
其中U是
| $ \begin{array}{*{20}{c}} {p(t) = {\psi _{k,j}}({Q_{k,j}}(t + 1)) = }\\ {{\psi _{k,j}}({Q_{k,j}}(t) + {{\hat e}_{k,j}}(t) - {{\hat p}_{k,j}}(t))} \end{array} $ | (26) |
由于
| $ p(t) = {\psi _{k,j}}({Q_{k,j}}(t) + {\hat e_{k,j}}(t)) $ | (27) |
李雅普诺夫DPP函数为
| $ \begin{array}{*{20}{c}} {\Delta L(t) + Vp(t) \le U + {\alpha _{k,j}}(t)[{{\hat e}_{k,j}}(t) - {\gamma _e}] + }\\ {V{\psi _{k,j}}({Q_{k,j}}(t) + {{\hat e}_{k,j}}(t))} \end{array} $ | (28) |
其中V≥0是系统稳定性和网络性能优化(开销最小化)之间的权衡系数.注意到式(28)中有些项和控制变量
| $ {\mathscr{P}_{l1}}:\mathop {{\rm{min}}}\limits_{({{\hat e}_{k,j}})} {\alpha _{k,j}}(t){\hat e_{k,j}}(t) + V{\psi _{k,j}}({Q_{k,j}}(t) + {\hat e_{k,j}}(t)) $ | (29a) |
| $ {\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\hat e_{k,j}}(t) \in [0,{C_j} - {Q_{k,j}}(t)] $ | (29b) |
对式(29)中的目标函数的删除控制变量求导得
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial {{\hat e}_{k,j}}(t)}}\left[ {{\alpha _{k,j}}(t){{\hat e}_{k,j}}(t) + } \right.}\\ {\left. {V{\psi _{k,j}}({Q_{k,j}}(t) + {{\hat e}_{k,j}}(t))} \right] = {\alpha _{k,j}}(t) - V\frac{\gamma }{{{C_j}}}} \end{array} $ | (30) |
导数为常数,故
| $ {\hat e_{k,j}}(t) = \left\{ {\begin{array}{*{20}{l}} {0,\quad {\alpha _{k,j}}(t) - V\frac{\gamma }{{{C_j}}} \ge 0}\\ {{C_j} - {Q_{k,j}}(t),\quad {\rm{ 其他 }}} \end{array}} \right. $ | (31) |
该部分通过Matlab仿真评估提出的方法的性能.假定基站的位置分布服从齐次泊松点过程,基站的初始状态分布为正态分布.在相邻两次删除分配之间,基站进行25次缓存分配.仿真参数如表 1所示.
|
|
表 1 仿真参数 |
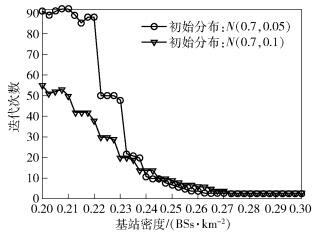
图 1展示了在不同的基站对于剩余存储空间的初始状态分布的条件下,MFG方法的计算复杂度(迭代次数)与基站密度的关系.无论初始分布如何,迭代次数都大体上随基站密度单调递减,并最终收敛至3.这表明,网络越密集,MFG方法的计算复杂度越低;迭代次数的最终收敛表明了当网络足够密集时,MFG方法的复杂度已经和网络密度无关了,迭代次数仅仅为3也充分证明了MFG方法能够在超密集网络中实现非常低的复杂度.所以,上述分析充分说明了MFG方法对于降低超密集网络缓存分配方法的复杂度有着巨大的意义.
|
图 1 MF方法迭代次数随基站密度的变化 |
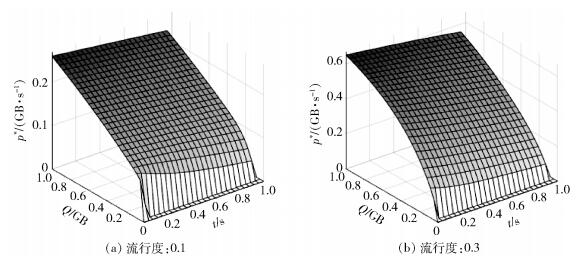
图 2给出了最优下载策略与剩余存储空间状态和时间的函数关系.
|
图 2 最优缓存策略 |
对于流行度较高的文件,下载速率也随之变高,所以MFG方法能够使得下载策略很好地适应文件流行度.其次,对于同一流行度、同一时刻,下载策略随剩余存储空间的单调递增表明了MFG方法对于空间状态的充分考虑.当空间较为充裕时,存储开销较小,可以较多地花费一些下载开销,从而能够较为充分地利用空闲的存储空间,为请求文件的用户服务;当剩余空间较少时,一方面存储开销较大,另一方面已有的缓存已经较多了,所以对于下载的需求较低,此时缓存分配的重点是减少下载开销.此外,对于同一流行度、同一剩余存储空间状态,下载策略随时间单调递减.这是因为MFG方法的优化目标是网络开销在[0, T]的积分,所以随着时间的推移,剩余的时间越来越少,缓存文件的意义也随之减小.上述的一切充分表明MFG方法在降低超密集网络缓存分配方法的复杂度的同时,既能够很好地保证基站缓存策略适应其自身状态,也能够很好地兼顾网络开销的最小化.
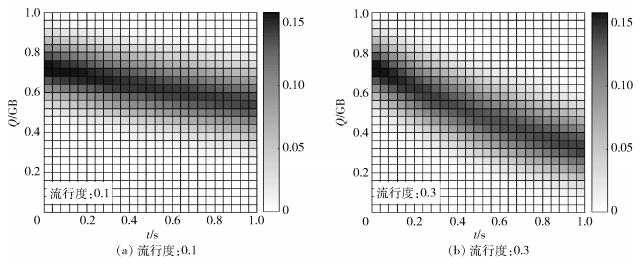
4.3 MFG方法的最优缓存策略图 3给出了MF分布随时间的变化.显然,当文件流行度较高时,MF分布的变化也越大.这再一次印证了MFG方法的下载策略能很好地适应文件流行度,MFG方法能够在降低超密集网络缓存分配方法的复杂度的同时很好地保证基站缓存策略适应其自身状态.
|
图 3 MF分布随时间的演化 |
本节将MFG方法与基本缓存方法[6]进行比较.基本缓存方法脱离了对内容重叠的考虑,在每个时刻基于当前的回程链路和存储状态,制定与瞬时文件流行度成比例的下载策略,如式(32)所示.
| $ p_j^*(t) = {B_j}(t) - \frac{1}{{1 + {R_k}(t){x_{k,j}}(t)}} $ | (32) |
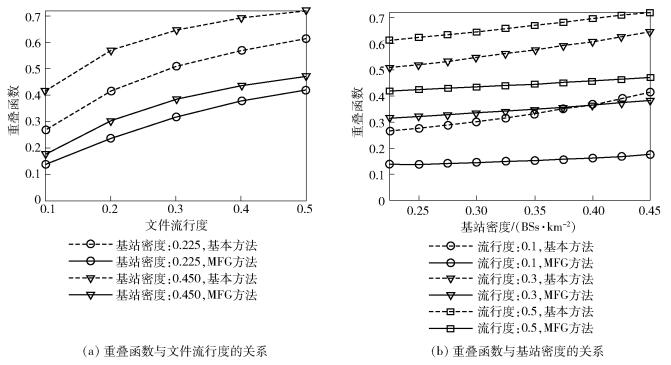
图 4(a)所示为MFG方法和基本方法的内容重叠函数与文件流行度的关系.对于较低的文件流行度(0.1),MFG方法能够比基本方法在0.225的网络密度下降低48.0%的内容重叠,在0.45的网络密度下降低57.8%.然而,随着文件流行度的增加,相比于基本方法,MFG方法带来的内容重叠下降率减小.当文件流行度为0.5时,在0.225的网络密度下降低31.5%,在0.45的网络密度下降低34.8%.这是因为当文件流行度较高时,对于下载的需求也较高,所以此时允许有较高的内容重叠,即此时对于内容重叠降低的需求较低,故此时MFG方法对于内容重叠的精确计算的优势相对不明显.然而,随着文件流行度的降低,降低内容重叠以减少网络开销愈发成为缓存分配的重点,所以MFG方法对于内容重叠的精确计算的优势愈发明显.
|
图 4 内容重叠函数比较 |
图 4(b)所示为内容重叠函数与网络密度的关系.对于较低的网络密度(0.225),MFG方法能够比基本方法在0.1的文件流行度下降低48.0%的内容重叠,在0.3的文件流行度下降低37.4%,在0.5的文件流行度下降低31.5%.随着网络密度的增加,相比于基本方法,MFG方法带来的内容重叠下降率减小.当网络密度为0.45时,在0.1的文件流行度下降低57.8%,在0.3的文件流行度下降低40.6%,在0.5的文件流行度下降低34.8%.所以,网络越密集,MFG方法的优势越明显,这表明了MF理论对于超密集网络的意义.
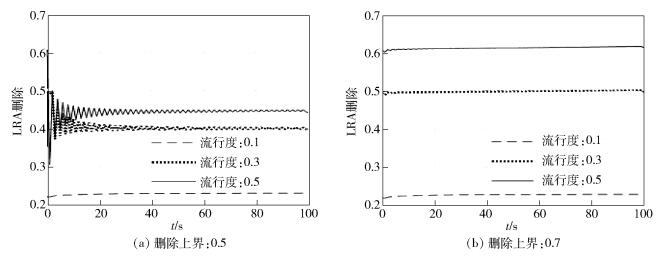
4.5 李雅普诺夫稳定性图 5在不同的LRA删除策略上界γe的条件下给出了不同文件流行度对应的LRA删除随时间的变化.
|
图 5 LRA删除随时间的演化 |
对于任意的文件流行度和γe,LRA删除都最终位于γe以下.而在LRA删除策略随时间的变化趋势上,有的是折线,有的则是平滑的曲线并且趋近于直线.在平滑的曲线上,每一个点都是位于γe以下的,即平滑的曲线对应的LRA删除在任意时刻都小于γe,而折线则不满足这一条件.其原因如下:采用李雅普诺夫DPP方法是为了保证系统的缓存-删除稳定性,即约束条件式(10e).若对于给定的删除策略上界γe来说,当文件流行度较低时,由于缓存的内容小于γe,此时即使不采用李雅普诺夫DPP方法,也能够满足系统稳定性的约束条件(LRA删除策略在γe以下),故此时DPP方法不起作用.例如,当流行度为0.3或0.5时,删除策略本身就低于0.7,故对于γe=0.7,DPP方法不起作用.若对于给定的删除策略上界γe来说,文件流行度较高,那么由于缓存的内容大于γe,此时若不采用李雅普诺夫DPP方法,则无法满足系统稳定性的约束条件.例如,当流行度为0.3或0.5时,删除策略本身大于0.5,故当γe为0.5时,DPP方法起作用.
4.6 总方法LRA开销比较本节将提出的方法整体与一个基本方法进行比较.基本方法中缓存分配方法已经在4.4节中提到,删除分配方法不考虑缓存-删除稳定性,仅仅制定最小化网络开销的删除策略.
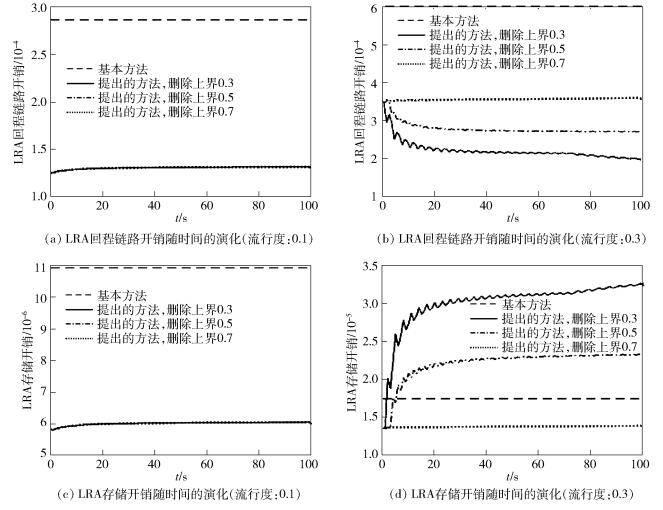
图 6给出了LRA回程链路开销和存储开销随时间的变化.需要注意的是,流行度为0.1时,提出的方法的3条线完全重合.由4.5节可知,这是因为此时DPP方法不起作用,故开销与γe无关.显然,对于两种流行度,提出的方法的LRA回程链路开销均完胜基本方法.结合4.5节中DPP方法何时起作用的结论可知,当DPP方法不起作用时,回程链路开销几乎不随时间变化,此时相比于基本方法的LRA回程链路开销的降低完全是MFG方法的功劳;当DPP方法起作用时,提出的方法的LRA回程链路开销先随时间递减,随后几乎不随时间变化,此时相比于基本方法的LRA回程链路开销的降低是MFG方法和DPP方法共同作用的结果.并且,对于给定的流行度,DPP方法起作用时的LRA回程链路开销小于不起作用时的开销;另外,对于DPP方法起作用的场景下,γe的值越低,LRA回程链路开销越小.故采用DPP方法不仅可以保证文件的缓存-删除稳定性,也可以通过减少反复地缓存和删除来降低回程链路开销.
|
图 6 LRA开销随时间的演化 |
对于LRA存储开销,结合4.5节中DPP方法何时起作用的结论可知,当DPP方法不起作用时,提出的方法的LRA存储开销完胜基本方法,这完全是MFG方法的功劳;而当DPP方法起作用时,提出的方法的LRA存储开销先随时间递增,并很快地高于基本方法,随后几乎不随时间变化,故此时是DPP方法对存储开销的增加盖过了MFG方法对存储开销的降低.因为DPP方法减少了对文件频繁的缓存和删除,故必然会增加对文件的存储,从而增加存储开销,其价值在于在删除分配时对流行度较高的文件进行一定程度的强制保留,且对于相同的流行度,γe的值越高,DPP方法起的作用越大,强制保留越积极,存储开销越大.结合前面的DPP方法对缓存-删除稳定性和回程链路开销降低的作用可知,DPP方法是以牺牲存储开销为代价换取缓存-删除稳定性和回程链路开销的策略.
5 结束语针对超密集网络中基于MFG和李雅普诺夫DPP方法的缓存和删除分配机制进行了研究.通过考虑CSI、基站存储状态信息和文件流行度状态信息等因素,采用动态SDG的模型对优化问题进行建模,并将这个具有严重耦合的博弈进行解耦,将其转化为MFG,通过分析研究得到超密集场景下最小化基站开销的缓存分配机制.在长时优化的文件删除分配策略上,根据李雅普诺夫理论将子问题转化为李雅普诺夫随机优化问题,并采用李雅普诺夫DPP方法实现了开销和系统稳定性之间的权衡.仿真结果表明,MFG方法在实现超密集网络缓存分配策略快速收敛的同时,既能够保证缓存分配策略很好地适应文件流行度和剩余存储空间状态,也能够很好地兼顾网络开销的最小化;网络密度越大,MFG方法越有意义;采用DPP方法能够在兼顾节约网络开销的同时保证系统的稳定性,且文件流行度越高,DPP方法的作用越明显.
附录:最优缓存策略的证明过程证明 MF-HJB方程式(19)的最小值项显然有其对应的最小值点:
| $ \begin{array}{*{20}{c}} {p_j^*(h,{Q_j},{x_j},t) = }\\ {\mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_{{p_j}(h,{Q_j},{x_j},t)} \left[ {{J_j}({p_j}(h,{Q_j},{x_j},t),{I^*}(t),I_j^{r*}(t)) + } \right.}\\ {G(t,h)\frac{{\partial {\varGamma _j}}}{{\partial h}} - {p_j}(h,{Q_j},{x_j},t)\frac{{\partial {\varGamma _j}}}{{\partial {Q_j}}} + }\\ {\left. {r({\mu _j} - {x_j})\frac{{\partial {\varGamma _j}}}{{\partial {x_j}}} + \frac{{{\zeta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _j}}}{{\partial {h^2}}} + \frac{{{\eta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _j}}}{{\partial x_j^2}}} \right]} \end{array} $ |
中括号里面的表达式对pj求偏导数得
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial {p_j}}}\left[ {{J_j}({p_j}(h,{Q_j},{x_j},t),{I^*}(t),I_j^{r*}(t)) + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} {G(t,h)\frac{{\partial {\varGamma _j}}}{{\partial h}} - {p_j}(h,{Q_j},{x_j},t)\frac{{\partial {\varGamma _j}}}{{\partial {Q_j}}} + }\\ {\left. {{\kern 1pt} {\kern 1pt} r({\mu _j} - {x_j})\frac{{\partial {\varGamma _j}}}{{\partial {x_j}}} + \frac{{{\zeta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _j}}}{{\partial {h^2}}} + \frac{{{\eta ^2}}}{2}\frac{{{\partial ^2}{\varGamma _j}}}{{\partial x_j^2}}} \right] = }\\ {\frac{\partial }{{\partial {p_j}}}\left[ {{J_j}({p_j}(h,{Q_j},{x_j},t),{I^*}(t),I_j^{r*}(t)) - } \right.} \end{array}\\ \begin{array}{*{20}{c}} {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {p_j}(h,{Q_j},{x_j},t)\frac{{\partial {\varGamma _j}}}{{\partial {Q_j}}}} \right] = }\\ {\frac{{\partial {J_j}({p_j}(h,{Q_j},{x_j},t),{I^*}(t),I_j^{r*}(t))}}{{\partial {p_j}}} - \frac{{\partial {\varGamma _j}(t)}}{{\partial {Q_j}}} = }\\ {\frac{\partial }{{\partial {p_j}}}\left[ {\frac{{{\phi _j}({p_j}(h,{Q_j},{x_j},t))[1 + I_j^{r*}(t)]}}{{R(h,{I^*}(t)){x_j}}} + } \right.} \end{array}\\ \begin{array}{*{20}{c}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\psi _j}({Q_j})} \right] - \frac{{\partial {\varGamma _j}(t)}}{{\partial {Q_j}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{1 + I_j^{**}(t)}}{{{\kern 1pt} R(h,{I^*}(t)){x_j}}}\frac{{\partial {\phi _j}({p_j}(h,{Q_j},{x_j},t))}}{{\partial {p_j}}} - } \end{array}\\ \begin{array}{*{20}{c}} {\frac{{\partial {\varGamma _j}(t)}}{{\partial {Q_j}}} = \frac{{1 + I_j^{r*}(t)}}{{R(h,{I^*}(t)){x_j}}}\frac{1}{{{B_j}(t) - {p_j}(h,{Q_j},{x_j},t)}} - }\\ {\frac{{\partial {\varGamma _j}(t)}}{{\partial {Q_j}}} = 0}\\ {p_j^*(h,{Q_j},{x_j},t) = {B_j}(t) - \frac{{1 + I_j^{r*}(t)}}{{R(h,{I^*}(t)){x_j}\frac{{\partial {\varGamma _j}}}{{\partial {Q_j}}}}}} \end{array} \end{array} $ |
证毕.
| [1] |
Chun B G, Chaudhuri K, Wee H, et al. Selfish caching in distributed systems:a game-theoretic analysis[M]. New York: Association for Computing Machinery, 2004: 21-30.
|
| [2] |
Yang C, Li J, Semasinghe P, et al. Distributed interference and energy-aware power control for ultra-dense D2D networks:a mean field game[J]. IEEE Transactions on Wireless Communications, 2017, 16(2): 1205-1217. DOI:10.1109/TWC.2016.2641959 |
| [3] |
Al-Zahrani A, Yu F R, Huang M. A joint cross-layer and co-layer interference management scheme in hyper-dense heterogeneous networks using mean-field game theory[J]. IEEE Transactions on Vehicular Technology, 2016, 65(3): 1522-1535. DOI:10.1109/TVT.2015.2413394 |
| [4] |
Baillieul J, Samad T. Encyclopedia of systems and control[M]. London: Springer London, 2014: 1-6.
|
| [5] |
Hamidouche K, Saad W, Debbah M, et al. Mean-field games for distributed caching in ultra-dense small cell networks[C]//American Control Conference. Boston: [s. n.], 2016: 4699-4704. https://www.researchgate.net/publication/305907497_Mean-Field_Games_for_Distributed_Caching_in_Ultra-Dense_Small_Cell_Networks
|
| [6] |
Kim H, Park J, Bennis M, et al. Ultra-dense edge caching under spatio-temporal demand and network dynamics[C]//IEEE International Conference on Communications (ICC). Paris: [s. n.] 2017: 1-7. https://www.researchgate.net/publication/313250248_Ultra-Dense_Edge_Caching_under_Spatio-Temporal_Demand_and_Network_Dynamics
|
| [7] |
Neely M J. Stochastic network optimization with application to communication and queueing systems[J]. Synthesis Lectures on Communication Networks, 2010, 3(1): 1-211. |
| [8] |
Huang L, Neely M J. Utility optimal scheduling in processing networks[J]. Performance Evaluation, 2011, 68(11): 1002-1021. DOI:10.1016/j.peva.2011.07.009 |
| [9] |
Samarakoon S, Bennis M, Saad W, et al. Ultra dense small cell networks:turning density into energy efficiency[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(5): 1267-1280. DOI:10.1109/JSAC.2016.2545539 |
| [10] |
张琪.联合缓存与无线传输的理论性能分析及优化策略研究[D].北京: 北京邮电大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10013-1018168967.htm
|
| [11] |
Cao Y, Tao M, Xu F, et al. Fundamental storage-latency tradeoff in cache-aided MIMO interference networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(8): 5061-5076. DOI:10.1109/TWC.2017.2705102 |
| [12] |
Gueant O, Lasry J, Lions P. Mean field games and applications[M]. Berlin, Germany: Springer Berlin Heidelberg, 2011: 205-266.
|
| [13] |
Bernt O. Stochastic differential equations[J]. IEEE Transactions on Automatic Control, 2006, 51(10): 1731-1732. DOI:10.1109/TAC.2006.882767 |
| [14] |
Debbah M, Couillet R, Perlaza S M, et al. Electrical vehicles in the smart grid:a mean field game analysis[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(6): 1086-1096. DOI:10.1109/JSAC.2012.120707 |
| [15] |
Aziz M, Caines P E. A mean field game computational methodology for decentralized cellular network optimization[J]. IEEE Transactions on Control Systems Technology, 2017, 25(2): 563-576. DOI:10.1109/TCST.2016.2558458 |
| [16] |
Li J, Chen Y T, Chen G, et al. Computational partial differential equations using matlab (Chapman & Hall/CRC Applied Mathematics & Nonlinear Science)[M]. New York: Taylor & Francis, 2011.
|



