无线共享网络的接入资源分散,容量有限,且价格互有差异,为了在保证用户满意度的同时提高运营商总体收益,需要对网络接入资源进行合理分配.因此,提出了一个基于博弈论的WiFi接入资源动态分配算法.首先,以总收益最大化为目标,兼顾用户满意度,建立基于斯塔克尔伯格博弈的网络接入资源动态分配模型;其次,通过两阶段博弈,运营商制定价格策略,激励用户执行网络选择策略,提出基于粒子群算法的网络资源动态分配求解算法,得出最优的网络价格及资源分配.仿真实验表明,算法能够实现接入资源的合理分配,在用户满意的同时实现运营商收益最大化.
The access resources of wireless shared network are scattered and limited in capacity and prices vary from one to another. To improve overall revenue of operators and ensure user satisfaction, the key is reasonably allocating access resources.Therefore, a game-based dynamic allocation algorithm of WiFi access resources is proposed. Firstly, aiming at maximizing overall revenue and taking user satisfaction into account, Stackelberg game-based dynamic allocation model is established. Secondly, through a two-stage game, the network-prices strategy which can motivate the users to select networks is generated by the operator. Then a dynamic allocation algorithm based on particle swarm optimization is proposed to obtain the optimal solution. Simulation shows that it can achieve reasonable allocation of resources which can maximize overall revenue while satisfying users.
近年来,WiFi技术因具有部署成本低和数据传输速率高的优点, 得到了快速发展,运营商通信网络持续向以分布式服务为核心的扁平化网络演进.无线共享网络则是基于分布式服务概念的新型网络,通过鼓励个人共享私有WiFi接入点(AP),快速、低成本聚集WiFi覆盖范围和容量[1].运营商甚至无需安装新的AP,即可拥有覆盖广泛的网络资源.对于用户,在家接入自己的AP,出门接入其他用户的AP,随时享受网络服务. FON网络就是旨在通过共享无线网络带宽,构筑全球性WiFi网络[2].目前无线共享网络市场发展仍然有限,为推动其建设和广泛应用,需要为利益相关者带来更加丰厚的回报以吸引其加入.即为用户提供更满意的服务,为网络管理者运营商带来更多的收益.
在无线共享网络中,私人WiFi接入点的特点是分布分散,且容量有限,需要使用有限的资源为所有用户提供满意的服务.此外,不同网络提供服务的能力不同,网络资源的定价互有差异,而每个用户的资源需求也互有差异,因此不同用户接入不同网络为运营商带来的收益互有差异.为用户提供满意的服务的同时最大化运营商的收益,关键在于为用户分配最合理的网络接入资源.
网络资源分配算法分为分布式和集中式两种[3].集中式方法中,运营商直接把用户分配到不同的网络接入资源.缺点是网络架构成本比较高.分布式方法中,用户自主选择接入网络,运营商不需在架构上投入额外成本.大多研究以分布式方法解决网络资源分配问题,模拟成博弈模型是较为普遍的方法,将用户、网络、运营商看作博弈玩家,玩家们努力最大化各自利益[4].
国内外学者多数以用户为中心,建立完全分布式资源分配模型[5-7]. Keshavarz-Haddad A等[5]模拟问题为非合作博弈模型,提出一个用户自主做出决策的分布式网络资源选择算法. Ortín J等[6]基于博弈理论框架,提出一个对数效用函数,最大化网络用户公平性. Feng X等[7]模拟问题为非对称拥塞博弈模型,用户以其余用户决策为前提作出最优选择.但大多没有考虑整体收益,导致运营商的总收益降低,称为“公地悲剧”[8].
此外,也有部分研究考虑了网络整体效益[9-10]. Dhifallah K等[9]利用非合作博弈模型模拟网络间竞争,保证用户的分布均衡,最大化用户吞吐量和网络收益.杜白等[10]基于网络剩余服务时间,引导用户的资源选择,提高网络总收益,降低用户阻塞率.这些研究大多追求数据速率或吞吐量等物理性能,却忽略了上层用户需求,没有考虑用户满意情况.
因此,需研究WiFi接入资源分配算法,保证运营商收益最大化的同时考虑用户满意度.受Courcoubetis C等[11]启发,运营商可制定价格激励机制,引导用户的选择.提出一个基于斯塔克尔伯格博弈的网络资源动态分配模型,运营商制定价格策略,激励用户做出网络选择,保证运营商收益最大化和用户的满意服务.提出基于粒子群算法的网络资源动态分配求解算法,得出最优的网络价格及接入资源分配.
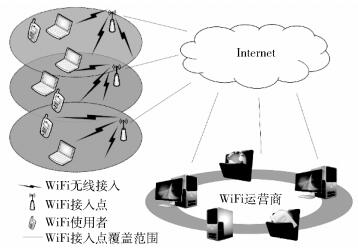
1 无线共享网络体系结构无线共享网络体系结构包含3种角色,如图 1所示,WiFi共享者,共享者提供私有WiFi组成网络接入资源池,并授予部分管理权限给运营商;WiFi运营商,是网络接入资源池的管理者,负责资源定价,并通过定价影响用户选择,完成网络资源的合理分配;移动用户,选择并接入一个WiFi资源,开启数据传输,结束后向运营商支付金钱.
|
图 1 无线共享网络体系结构 |
在t时刻,一个无线共享网络中各个资源覆盖区域和预接入用户的相对地理位置保持不变.预接入用户是指想要接入但尚未确定网络接入资源的用户.每个网络资源服务能力的初始值(如:数据传输速率)和用户的数据传输量是已知常量.有些WiFi的覆盖区域存在重叠,位于重叠区域的预接入用户可接入的网络数量多于1个,运营商通过定价影响用户的网络选择完成资源分配过程,最后每个预接入用户能且只能连入1个网络.
用户诉求是选择性价比最高的网络,即价格低、速率高.价格是指网络接入资源间的相对价格,不同网络价格和数据传输速率互不相同.网络价格由运营商预设,网络数据传输速率取决于网络拥挤程度;运营商核心诉求是总收益最大化,这与网络价格、用户的网络选择、用户的数据传输量直接相关.
2 基于斯塔克尔伯格的网络资源动态分配模型在无线共享网络体系结构中,运营商先做价格策略,用户再执行网络选择策略,二者并不平等,符合两阶段斯塔克尔伯格博弈模型中领导者和跟随者的关系.运营商是领导者,用户是跟随者,运营商制定价格策略以使总体收益最大化,然后用户执行网络选择策略以使个体收益最大化.为了准确的定义博弈目标,描述博弈过程,本章定义了用于描述运营商和用户各自收益的效用函数.
2.1 运营商效应函数定义效用函数前,先定义运营商网络价格策略,P=(p1, p2, …, pN)分别表示第1个,第2个,…, 第N个网络价格,这里指网络接入资源间相对价格.用运营商效用函数描述所有资源带来的总收入,等于每个网络各自收入的加和,每个网络收入等于使用本网络传输的数据量与传输价格的乘积.
| $ U(\mathit{\boldsymbol{p}}) = \sum\limits_{j = 1}^N {{p_j}} {X_j} = \sum\limits_{j = 1}^N {{p_j}} \sum\limits_{i = 1}^{{n_j}} {{x_i}} $ | (1) |
其中:N为网络数量,Xj为接入网络j的数据传输总量,xi为用户i传输的数据量,nj为网络j的接入用户数量.
2.2 用户效用函数首先定义用户的网络选择策略.以图 1为例,3个WiFi网络由于覆盖区域存在重叠被分为5个子区域,从左至右,用户数依次为U1、U2、U3、U4、U5,仅有区域2和区域4的用户需要做出网络选择并参与博弈.参与者i的策略sij(si∈si)指参与者i可以选择接入的网络组成的策略集合. si=1,即用户i选择接入网络1.区域2和区域4中用户的策略集合分别为Si2={1, 2}和Si2={2, 3}.
用用户效用函数描述用户收益.用户诉求是获得满意的服务,为使用公式量化用户满意情况,使用用户的预期与实际情况之间的差值来描述用户满意值.即,用户获得的收益是用户预期支付的价格与实际支付价格的差异带来的支付总金额的差异.
使用用户愿意支付的最高价格来表示用户预期支付的价格.其中,数据传输速率越高,用户愿意支付的价格越高.基于边际效应递减规律[14],建立1个递增凹函数模型.
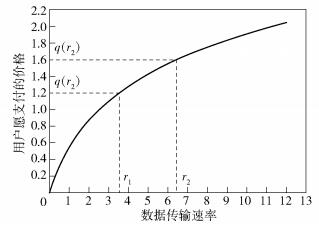
实际情境中,用户愿意支付的价格由用户因素、业务类型等多方面因素综合确定.如图 2所示的函数,当传输速率为0时,用户不愿意支付,传输速率为r1,用户愿意支付的价格为q(r1),传输速率为r2,用户愿意支付的价格为q(r2),q(r2)-q(r1)是数据传输速率提高获得的愿意支付的价格的增长.
|
图 2 用户愿意支付的价格与数据传输速率 |
使用下式作为上述模型的一个实例:
| $ q(r) = \alpha {\rm{log}}(1 + r) $ | (2) |
其中:r为网络数据传输速率,α为常数.
用户愿意支付的价格与数据传输速率有关,而数据传输速率取决于网络拥塞程度,使用R(n)表示当有n个用户同时接入一个WiFi网络时该网络的数据传输速率.根据IEEE 802.11g标准,
| $ \bar R(n) = \frac{{\tau {\kern 1pt} {\kern 1pt} {{\bar \tau }^{n - 1}}L}}{{{{\bar \tau }^n}{T_{\rm{b}}} + [(1 - {{\bar \tau }^n}) - n\tau {\kern 1pt} {\kern 1pt} {{\bar \tau }^{n - 1}}]{T_{\rm{c}}} + n\tau {\kern 1pt} {\kern 1pt} {{\bar \tau }^{n - 1}}{T_{\rm{s}}}}} $ | (3) |
其中:τ为平均竞争成功率(τ=1-τ),L为平均负载长度, Tb为退避窗口长度,Tc为碰撞窗口长度,Ts为成功窗口长度.随着用户数量的增加,网络平均资源减少,且用户间竞争产生资源浪费,用户获得的数据传输速率下降.
πi(Y)表示用户i在策略组合Y下的效用函数.
| $ {\pi _i}(Y) = {q_j}({r_j}({n_j}(Y))){x_i} - {p_j}{x_i} $ | (4) |
其中:在策略组合Y下,si=j;nj(Y)为在策略组合Y下网络j的用户数量;rj(nj(Y))为在用户数量为nj(Y)的情况下网络j的数据传输速率;qj(rj(nj(Y)))为在数据传输速率为rj(nj(Y))的情况下,用户愿意向网络j支付的最高价格;pj表示网络实际价格.
3 基于粒子群算法的网络资源动态分配算法针对第2节提出的网络资源动态分配模型,基于逆向归纳法的求解思想设计一种网络资源动态分配算法.运营商每制定1次价格策略,用户制定1次网络选择策略为1个轮次,领导者运营商知晓用户上一轮次的选择.算法流程为,博弈双方制定初始化策略;运营商基于对用户的了解调整价格,博弈双方制定第2轮策略;然后制定第3轮策略,直到纳什均衡时双方无法单方面提高效用.博弈者制定策略是求解最优化问题,同时搜索多个取值可以减少循环次数,提高计算速度.
3.1 初始化策略求解模型的第1轮次运营商制定初始化网络价格策略,用户根据初始价格制定网络选择策略.
设置初始粒子的位置、速度、长度和粒子规模.
| $ \begin{array}{l} \mathit{\boldsymbol{p}}(t) = [{\mathit{\boldsymbol{p}}_1}(t),{\mathit{\boldsymbol{p}}_2}(t), \cdots ,{\mathit{\boldsymbol{p}}_M}(t)]\\ {\mathit{\boldsymbol{p}}_i}(t) = ({p_{{i_1}}},{p_{{i_2}}}, \cdots ,{p_{{i_N}}}) \end{array} $ | (5) |
| $ \begin{array}{l} \mathit{\boldsymbol{v}}(t) = [{\mathit{\boldsymbol{v}}_1}(t),{\mathit{\boldsymbol{v}}_2}(t), \cdots ,{\mathit{\boldsymbol{v}}_M}(t)]\\ {\mathit{\boldsymbol{v}}_i}(t) = ({v_{{i_1}}},{v_{{i_2}}}, \cdots ,{v_{{i_N}}}) \end{array} $ | (6) |
其中:t为迭代次数;pi(t)为位置,对应网络价格;v(t)表示速度;N是粒子长度,对应网络个数;M是粒子规模.对每个粒子,根据pi(t),使用离散量子粒子群算法[12]计算用户网络选择策略Y*[pi(t)],其中,使用二进制值表示网络的选择与否,策略的表示形式是一串二进制数.
3.2 运营商网络价格策略从第2轮开始,运营商基于上一轮的网络选择调整网络价格.寻找使运营商效用函数达到最大值的网络价格的取值,是一个典型的最优化问题,使用经典粒子群算法即可求解.
将运营商的效用函数作为适应度函数.
| $ U(\mathit{\boldsymbol{p}}) = \sum\limits_{j = 1}^N {{p_j}} {X_j} = \sum\limits_{j = 1}^N {{p_j}} \sum\limits_{i = 1}^{{n_j}} {{x_i}} $ | (7) |
然后根据用户网络选择策略Y*和适应度函数,计算每个粒子的适应值L[pi(t)].寻找个体最佳适应值和全局最佳适应值pbest(t)和gbest(t),其中,
| $ {\mathit{\boldsymbol{p}}_{best}}(t) = ({p_{bes{t_1}}}(t),{p_{bes{t_2}}}(t), \cdots ,{p_{bes{t_M}}}(t)) $ | (8) |
然后根据更新公式更新粒子位置和速度:
| $ \begin{array}{l} {\mathit{\boldsymbol{v}}_i}(t + 1) = w{\mathit{\boldsymbol{v}}_i}(t) + {\mu _1} {\rm{rand}} ({\kern 1pt} {\kern 1pt} )[{\mathit{\boldsymbol{p}}_{{\rm{ best}}{{\rm{ }}_i}}}(t) - {\mathit{\boldsymbol{p}}_i}(t)] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mu _2} {\rm{rand}} ({\kern 1pt} {\kern 1pt} )[{g_{{\rm{ best }}}}(t) - {\mathit{\boldsymbol{p}}_i}(t))] \end{array} $ | (9) |
| $ {\mathit{\boldsymbol{p}}_i}(t + 1) = {\mathit{\boldsymbol{p}}_i}(t) + {\mathit{\boldsymbol{v}}_i}(t + 1) $ | (10) |
其中:pi(t+1)和vi(t+1)表示第t+1轮迭代的位置和速度.更新后的网络价格表示为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{p}}(t + 1) = [{\mathit{\boldsymbol{p}}_1}(t + 1),{\mathit{\boldsymbol{p}}_2}(t + 1), \cdots ,{\mathit{\boldsymbol{p}}_M}(t + 1)]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{p}}_i}(t + 1) = ({p_{{i_1}}},{p_{{i_2}}}, \cdots ,{p_{{i_N}}})} \end{array} $ | (11) |
若全局最佳适应值连续4次保持不变,找到最优解;否则,再次使用更新公式更新网络资源价格.
3.3 用户网络选择策略在每一轮次,运营商制定价格策略后,用户执行网络选择策略,这也是一个最优化问题,最优解是使得用户效用函数达到最优值的网络选择的取值.由于网络选择的取值不是常规类型的连续变量,基于离散量子粒子群算法[12],可以解决变量值不连续的问题.使用二进制数字表示用户的网络选择策略,二进制数字的长度取决于可接入的网络数量,二进制数字的位值表示对应网络选择与否.
以图 1为例,从左至右有5个子区域,博弈参与者为区域2和区域4的用户,由于可接入网络数量为2,每个用户对应1个长度为2的二进制数字,分别表示2个可接入网络的选择情况,取值为1表示选择,取值为0表示不选择.网络选择结果为每个用户能且只能接入1个网络,全0或2个位值等于1或2个以上位值等于1时,策略无效.策略组合Y的表示是将所有二进制数字依次连接,长度为1×(U2×2+U4×2).最优策略组合Y使适应值最大.
基于用户的效用函数,建立适应度函数如下.
如果Y为有效策略,
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f\left( Y \right) = \\ \sum\limits_{i = 1}^U {{\rm{max}}} \{ v(\left. Y \right\|{{\kern 1pt} _{s_i^n}},Y),0|n = 1,2, \cdots ,{N_{{\rm{length}}}}({S_i})\} \end{array} $ | (12) |
如果Y为无效策略,
| $ f\left( Y \right) = L $ |
其中v(Y‖sin, Y)=πi(Y‖sin)-πi(Y).
初始化量子粒子向量、离散粒子向量、粒子长度和粒子规模.
| $ \begin{array}{l} \mathit{\boldsymbol{Q}}(t) = [{\mathit{\boldsymbol{q}}^1}(t),{\mathit{\boldsymbol{q}}^2}(t), \cdots ,{\mathit{\boldsymbol{q}}^M}(t)]\\ {\mathit{\boldsymbol{q}}^j}(t) = (q_1^j,q_2^j, \cdots ,q_N^j) \end{array} $ | (13) |
| $ \begin{array}{l} \mathit{\boldsymbol{P}}(t) = [{\mathit{\boldsymbol{p}}^1}(t),{\mathit{\boldsymbol{p}}^2}(t), \cdots ,{\mathit{\boldsymbol{p}}^M}(t)]\\ {\mathit{\boldsymbol{p}}^j}(t) = (p_1^j,p_2^j, \cdots ,p_N^j) \end{array} $ | (14) |
其中:Q(t)为量子粒子向量,P(t)为离散粒子向量,N为粒子长度,M为粒子规模.根据适应度函数,离散粒子向量的适应值f(pj(t)).寻找个体最佳适应值和全局最佳适应值pbest(t)和gbest(t).
| $ {\mathit{\boldsymbol{p}}_{{\rm{ best }}}}(t) = ({p_{{\rm{ best}}{{\rm{ }}_{\rm{1}}}}}(t),{p_{{\rm{ best}}{{\rm{ }}_{\rm{2}}}}}(t), \cdots ,{p_{{\rm{ best}}{{\rm{ }}_M}}}(t)) $ | (15) |
量子粒子向量的更新公式为
| $ \mathit{\boldsymbol{q}}_{{\rm{ self, best }}}^j(t) = \alpha \mathit{\boldsymbol{p}}_{{\rm{ self, best }}}^j(t) + \beta (1 - \mathit{\boldsymbol{p}}_{{\rm{ self, best }}}^j(t)) $ | (16) |
| $ {q_{{\rm{ global }},{\rm{ best }}}}(t) = \alpha {p_{{\rm{ global }},{\rm{ best }}}}(t) + \beta (1 - {p_{{\rm{ global }},{\rm{ best }}}}(t)) $ | (17) |
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{q}}^j}(t + 1) = }\\ {{c_1}{\mathit{\boldsymbol{q}}^j}(t) + {c_2}\mathit{\boldsymbol{q}}_{{\rm{ self,best }}}^j(t) + {c_3}{q_{{\rm{ global,best }}}}(t)} \end{array} $ | (18) |
根据Q(t),离散粒子向量更新公式为
| $ \begin{array}{*{20}{c}} {{\rm{if}}{\kern 1pt} {\rm{: rand }} > q_i^j(t)\forall j \in N[1,M],i \in N[1,N]}\\ {p_i^j(t) = 1}\\ {{\rm{ else }}:p_i^j(t) = 0} \end{array} $ | (19) |
当全局最佳适应值等于0时停止更新,找到最优解.否则,再次使用更新公式更新量子粒子向量和离散粒子向量.
网络资源动态分配算法流程如下:
1 第1部分运营商制定网络价格策略阶段.
2 输入网络选择Y*[pi(t)]、粒子位置p(t)和速度v(t),计算适应值L[pi(t)],Find pbest(t), gbest(t).
3 While gbest(t)尚未连续4次相同, do
4 更新粒子速度和位置pi(t+1)=pi(t)+vi(t+1)
5 计算适应值L[pi(t+1)],Find pbest(t+1), gbest(t+1)
6 end while
7 第2部分为用户执行网络选择策略.
8 初始化量子粒子向量Q(t)和离散粒子向量P(t),计算适应值f(pj(t)),Find pbest(t), gbest(t).
9 While gbest(t)!=0, do
10 更新量子粒子向量和离散粒子向量
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{q}}^j}(t + 1) = {c_1}{\mathit{\boldsymbol{q}}^j}(t) + {c_2}\mathit{\boldsymbol{q}}_{{\rm{self,best}}}^j(t) + {c_3}{q_{{\rm{global,best}}}}\\ (t) \end{array} $ |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}}{\kern 1pt} {\rm{: rand }} > q_i^j(t)\forall j \in N[1,M],i \in N[1,N],\\ p_i^j(t) = 1 \end{array} $ |
| $ {\rm{else }}:p_i^j(t) = 0 $ |
11 计算适应值f(pj(t+1))Find pbest(t+1), gbest(t+1)
12 end while
4 仿真结果与分析为了验证算法效果,采用Matlab软件进行仿真实验. 3个WiFi共享者提供3个WiFi接入点,3个WiFi网络两两重叠如图 1所示.参数设置见表 1.
|
|
表 1 网络参数设置 |
子区域2和4的用户数为5和10,编号后用户需要传输的数据量分别为10、11、12、13、14、4、5、2、8、10、12、12、13、14和2MB.
粒子群优化算法参数设置和离散量子粒子群算法参数设置见表 2和表 3.完成参数设置后,为验证策略有效性,实现基于拥塞博弈的分布式网络资源分配策略[7],并与第3节策略对比.
|
|
表 2 粒子群优化算法参数设置 |
|
|
表 3 离散量子粒子群算法参数设置 |
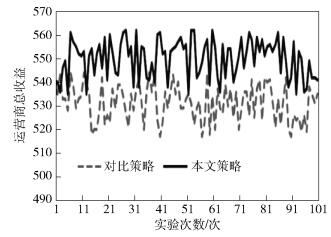
在用户满意度相差不大时,运行100次并对资源分配结果的运营商总收入进行比较,结果如图 3所示.
|
图 3 运营商总收益对比 |
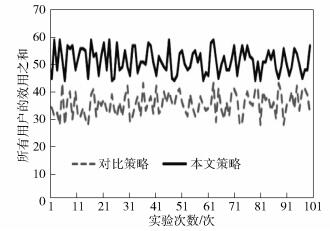
实验结果表明,在用户满意情况相差不大的情况下,第3节所述的接入资源分配策略可以为运营商带来更高的收入,从而促进运营商的积极性,推进网络建设及应用,如图 4所示.
|
图 4 用户满意度情况对比 |
在运营商总收入基本持平的情况下,运行100次对用户满意度情况进行比较.实验结果表明,在运营商总收入相差不大的情况下,第3节中的资源分配策略总是可以为用户提供更加满意的服务.
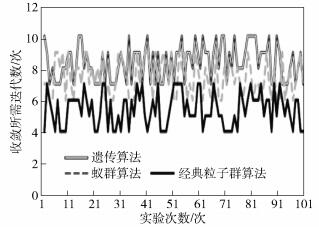
进一步分析算法性能,运营商制定价格策略阶段,已知网络选择策略,采用经典粒子群优化算法、蚁群算法、遗传算法进行仿真,时间复杂度为O(TM),T为迭代次数,M为粒子规模.运行100次并对收敛所需迭代次数进行对比,如图 5所示.
|
图 5 制定网络价格策略阶段算法迭代次数 |
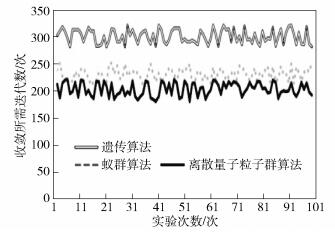
在用户制定网络选择策略阶段,输入已知的网络价格策略,采用离散量子粒子群算法、蚁群算法、遗传算法进行仿真,算法时间复杂度为O(TM).同样运行100次并对收敛所需迭代次数进行对比,如图 6所示.
|
图 6 制定网络选择策略阶段算法迭代次数 |
在运营商制定价格策略阶段,和遗传算法、蚁群算法相比,经典粒子群算法具有更低的迭代次数.在用户制定网络选择策略阶段,离散量子粒子群算法比遗传算法和蚁群算法需要更低的迭代次数.
| [1] |
Giarre L, Neglia G, Tinnirello I. Resource sharing optimality in WiFi infrastructure networks[C]//Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 200928th Chinese Control Conference. New York: IEEE Press, 2009: 5877-5882. https://www.researchgate.net/publication/224108511_Resource_sharing_optimality_in_WiFi_infrastructure_networks
|
| [2] |
李清莲. 从BT FON看电信运营商WiFi商业模式创新[J]. 广东通信技术, 2008, 28(6): 5-8. Li Qinglian. Research on telecom business WiFi business model innovation from BT FON[J]. Guangdong Communication Technology, 2008, 28(6): 5-8. DOI:10.3969/j.issn.1006-6403.2008.06.002 |
| [3] |
Haddad M, Elayoubi S E, Altman E, et al. A hybrid approach for radio resource management in heterogeneous cognitive networks[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(4): 831-842. DOI:10.1109/JSAC.2011.110414 |
| [4] |
Du Zhiyong, Wu Qihui, Yang Panlong, et al. User-demand-aware wireless network selection:a localized cooperation approach[J]. IEEE Transactions on Vehicular Technology, 2014, 63(9): 4492-4507. DOI:10.1109/TVT.2014.2316533 |
| [5] |
Keshavarz-Haddad A, Aryafar E, Wang M, et al. HetNets selection by clients:convergence, efficiency, and practicality[J]. ACM Transactions on Networking, 2017, 25(1): 406-419. DOI:10.1109/TNET.2016.2587622 |
| [6] |
Ortín J, Gállego J R, Canales M. Joint cell selection and resource allocation games with backhaul constraints[J]. Pervasive and Mobile Computing, 2017, 35: 125-145. DOI:10.1016/j.pmcj.2016.06.009 |
| [7] |
Feng Xinxin, Gan Xiaoying, Zheng Haifeng, et al. Distributed cell selection in heterogeneous wireless networks[J]. Computer Communications, 2017, 109: 13-23. DOI:10.1016/j.comcom.2017.05.005 |
| [8] |
Elayoubi S E, Altman E, Haddad M, et al. A hybrid decision approach for the association problem in heterogeneous networks[C]//2010 Proceedings IEEE INFOCOM. New York: IEEE Press, 2010: 1-5. http://www.oalib.com/paper/4079920
|
| [9] |
Dhifallah K, Gourhant Y, Senouci S M. Cell selection game in heterogeneous macro-small cell networks[C]//2017 IEEE International Conference on Communications (ICC). New York: IEEE Press, 2017: 1-6. https://www.researchgate.net/publication/318805759_Cell_selection_game_in_heterogeneous_macro-small_cell_networks
|
| [10] |
杜白, 李红艳. 一种采用剩余服务时间的异构网络选择算法[J]. 西安电子科技大学学报(自然科学版), 2016(1): 7-11. Du Bai, Li Hongyan. A heterogeneous network selection algorithm using remaining service time[J]. Journal of Xidian University (Natural Science Edition), 2016(1): 7-11. DOI:10.3969/j.issn.1001-2400.2016.01.002 |
| [11] |
Courcoubetis C, Weber R. Pricing communication networks[M]. Hoboken: Wiley, 2003.
|
| [12] |
Shuyuan Yang, Min Wang, Licheng Jiao. A quantum particle swarm optimization[C]//Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753). Portland: [s.n.], 2004: 320-324. https://link.springer.com/chapter/10.1007/11795131_63
|


