2. 西北工业大学 机电学院, 西安 710072;
3. 东莞市三航军民融合创新研究院, 东莞 523808
为提高非平稳噪声下远场非相干窄带信号波达方向(DOA)的估计精度,提出了一种基于稀疏重构的DOA估计算法.采用类协方差差分算法构造差分矩阵,抑制非平稳噪声的影响;基于类旋转不变子空间参数估计算法基本原理构造稀疏表示模型与权函数;利用加权l1范数对模型求解,实现DOA估计.仿真结果表明,与传统的协方差差分算法、噪声协方差矩阵估计算法、秩迹最小化算法以及稀疏重构算法相比,所提算法不仅能较好地抑制非平稳噪声的影响,而且在低信噪比、低快拍数情况下具有较强的稳健性和较高的估计精度.
2. School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China;
3. Dongguan Sanhang Civil-Military Integration Innovation Institute, Dongguan 523808, China
In order to improve the direction of arrival (DOA) estimation accuracy of the far-field non-coherent narrow-band signal in non-stationary noise environment, an improved DOA estimation algorithm based on sparse reconstruction is proposed. Firstly, the class differential covariance algorithm is used to construct the difference matrix to suppress the influence of non-stationary noise. Then the sparse representation model and the weight function is constructed based on the basic principle of estimation of signal parameters via rotational invariance technique algorithm. Finally, the DOA estimation is realized by solving the model with weighted l1 norm. Simulation shows that, compared with the traditional covariance difference algorithm, the noise covariance matrix estimation algorithm, the rank trace minimization algorithm, the sparse reconstruction algorithm, the proposed algorithm can not only suppress the influence of non-stationary noise effectively, but also has strong robustness and high estimation accuracy under low signal noise ratio and low snapshot number.
波达方向(DOA, direction of arrival)估计是阵列信号处理研究的重要内容,在雷达、无线通信以及电子对抗等领域有着广泛的应用[1].传统的DOA估计算法[2-3]均假设阵元噪声为高斯均匀白噪声,而在实际应用中,当天线阵元未准确校正或接收通道硬件存在差异时,接收到的噪声呈现空时不相关但非均匀的特性,即空间非平稳噪声、阵元噪声功率各不相等[4].
近年来,不少学者对空间非平稳噪声下的DOA估计进行了广泛的研究.例如,Qi等[5]提出广义协方差差分(GCD, generalized covariance difference)算法,通过构造差分矩阵抑制非平稳噪声的影响,再结合子空间算法得到DOA估计值,但GCD算法在DOA估计时会出现对称伪峰.吴云韬等[6]提出一种噪声协方差矩阵估计(NCME, noise covariance matrix estimation)算法,通过将协方差矩阵分块处理,并以分块矩阵之间的关系估计出非平稳噪声协方差矩阵,在减去非平稳噪声估计矩阵后,应用子空间算法得到DOA估计.基于此,汪弟杰等[7]将NCME算法与求根MUSIC算法相结合,降低了计算复杂度. Liao等[8]则提出一种协方差矩阵秩迹最小化(RTM, rank and trace minimization)算法,利用协方差矩阵低秩特性,将无噪声协方差矩阵低秩问题转化为噪声功率最大化问题,以此估计出未知的非均匀噪声功率,而后利用接收信号和非均匀噪声协方差矩阵之差实现DOA估计.王洪雁等[9]将RTM算法与空间平滑算法相结合,实现非平稳噪声下相干信源的DOA估计.然而,NCME算法与RTM算法必须满足阵元数大于等于信源数的3倍,当不满足此条件时,这2种算法的估计性能将会降低甚至失效.
上述算法存在的另一个问题是在低信噪比(SNR,signal noise ratio)和声源相距较近的情况下,会出现谱峰混叠现象,导致无法得到准确的DOA估计值.近年来,随着稀疏重构理论的提出和广泛应用,学者们将稀疏重构应用于DOA估计中,极具代表性的是l1-SVD算法[10-12],然而,当噪声为空间非平稳噪声时,由于阵列观测信号模型中存在未知的非平稳噪声会影响SVD分解,故导致l1-SVD算法失效.
为解决上述问题,将类协方差差分算法与类旋转不变子空间参数估计(ESPRIT-Like, estimation of signal parameters via rotational invariance technique- Like)算法[13]相结合,提出了一种非平稳噪声下基于稀疏重构的DOA估计算法.该算法利用类协方差差分技术抑制非平稳噪声的影响,降低非平稳噪声对定位精度的影响;同时基于ESPRIT-Like算法的原理构造稀疏表示模型和权函数,通过解此稀疏表示模型,实现DOA估计.仿真结果验证了该算法的性能.
1 信号模型假设K个相互独立的远场窄带信号入射到M=2L+1(M>2K)个阵元的均匀线阵上,阵元间距为半波长,则阵列观测信号模型为
| $ \mathit{\boldsymbol{X}}(t) = \mathit{\boldsymbol{AS}}(t) + \mathit{\boldsymbol{N}}(t),t = 1,2, \cdots ,T $ | (1) |
其中:S(t)=[s1(t), s2(t), …, sK(t)]T为信号向量,A=[a(θ1), a(θ2), …, a(θK)]为阵列导向矩阵
| $ \mathit{\boldsymbol{R}} = E\{ \mathit{\boldsymbol{X}}(t){\mathit{\boldsymbol{X}}^{\rm{H}}}(t)\} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_S}{\mathit{\boldsymbol{A}}^{\rm{H}}} + \mathit{\boldsymbol{Q}} $ | (2) |
其中:RS=E{S(t)SH(t)}为信号协方差矩阵,Q为噪声协方差矩阵.当噪声为高斯白噪声时,Q=diag{σ2, …, σ2}为M×M维矩阵,当噪声为非平稳噪声时,Q=diag{σ12, σ22, …, σM2}.
2 算法原理 2.1 类协方差差分算法ESPRIT-Like算法需满足导向矩阵为列满秩矩阵,而GCD算法引入的M×M维置换矩阵J并不能满足此条件,因此该算法引入一个M×M维对称对角变换矩阵
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{R}}_D} = \mathit{\boldsymbol{BR}}{\mathit{\boldsymbol{B}}^{ - 1}} - {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{RB}} = }\\ {[\mathit{\boldsymbol{BA}},{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{A}}]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_S}}&{}\\ {}&{ - {\mathit{\boldsymbol{R}}_S}} \end{array}} \right]{{[\mathit{\boldsymbol{BA}},{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{A}}]}^{\rm{H}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{A}}_D}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_S}}&{}\\ {}&{ - {\mathit{\boldsymbol{R}}_S}} \end{array}} \right]\mathit{\boldsymbol{A}}_D^{\rm{H}}} \end{array} $ | (3) |
其中:AD=[BA, B-1A]为M×2K维虚拟导向矩阵[14],矩阵AD的第k和k+K列分别为Ba(θk)和B-1a(θk).令ωk=2πdsin θk/λ,则有
| $ \mathit{\boldsymbol{Ba}}({\theta _k}) = {[{{\rm{e}}^{{\rm{j}}L\phi }},{{\rm{e}}^{{\rm{j}}(L - 1)\phi - {\rm{j}}{\omega _k}}}, \cdots ,{{\rm{e}}^{{\rm{j}}L\phi - {\rm{j}}(M - 1){\omega _k}}}]^{\rm{T}}} $ | (4) |
| $ {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{a}}({\theta _k}) = {[{{\rm{e}}^{ - {\rm{j}}L\phi }},{{\rm{e}}^{ - {\rm{j}}(L - 1)\phi - {\rm{j}}{\omega _k}}}, \cdots ,{{\rm{e}}^{ - {\rm{j}}L\phi - {\rm{j}}(M - 1){\omega _k}}}]^{\rm{T}}} $ | (5) |
可知,当M>2且ϕ≠0时,导向矩阵AD为列满秩矩阵,但若将矩阵B换成矩阵J,矩阵AD并不会为列满秩矩阵.
2.2 ESPRIT-Like算法对导向矩阵AD的行按[2L,1]与[1, 2L]进行分块处理:
| $ {\mathit{\boldsymbol{A}}_D} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{D11}}}\\ {{\mathit{\boldsymbol{A}}_{D12}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{D21}}}\\ {{\mathit{\boldsymbol{A}}_{D22}}} \end{array}} \right] $ | (6) |
其中:AD11和AD22均为2L×2K维导向矩阵.定义2L×2L维置换矩阵J,则有
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{D11}} = [{\mathit{\boldsymbol{B}}_{D1}}{\mathit{\boldsymbol{a}}_{D11}}({\theta _1}), \cdots ,{\mathit{\boldsymbol{B}}_{D1}}{\mathit{\boldsymbol{a}}_{D11}}({\theta _K}),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{B}}_{D1}^{ - 1}{\mathit{\boldsymbol{a}}_{D11}}({\theta _1}), \cdots ,\mathit{\boldsymbol{B}}_{D1}^{ - 1}{\mathit{\boldsymbol{a}}_{D11}}({\theta _K})] \end{array} $ | (7) |
| $ \begin{array}{l} \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{A}}_{D22}} = [\mathit{\boldsymbol{D}}({\theta _1}){\mathit{\boldsymbol{B}}_{D1}}{\mathit{\boldsymbol{a}}_{D11}}({\theta _1}), \cdots ,\mathit{\boldsymbol{D}}({\theta _K}){\mathit{\boldsymbol{B}}_{D1}}{\mathit{\boldsymbol{a}}_{D11}}({\theta _K}),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{D}}({\theta _1})\mathit{\boldsymbol{B}}_{D1}^{ - 1}{\mathit{\boldsymbol{a}}_{D11}}({\theta _1}), \cdots ,\mathit{\boldsymbol{D}}({\theta _K})\mathit{\boldsymbol{B}}_{D1}^{ - 1}{\mathit{\boldsymbol{a}}_{D11}}({\theta _K})] \end{array} $ | (8) |
其中
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{B}}_{D1}}{\mathit{\boldsymbol{a}}_{D11}}({\theta _k}) = [{{\rm{e}}^{{\rm{j}}(L - 0)\phi }}, \cdots ,{{\rm{e}}^{{\rm{j}}(L - L)\phi - {\rm{j}}L{\omega _k}}}, \cdots ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{e}}^{{\rm{j}}(L - 1)\phi - {\rm{j}}(M - 2){\omega _k}}}{]^{\rm{T}}}} \end{array} $ | (9) |
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{B}}_{D1}^{ - 1}{\mathit{\boldsymbol{a}}_{D11}}({\theta _k}) = [{{\rm{e}}^{ - {\rm{j}}(L - 0)\phi }}, \cdots ,{{\rm{e}}^{ - {\rm{j}}(L - L)\phi - {\rm{j}}L{\omega _k}}}, \cdots ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{e}}^{ - {\rm{j}}(L - 1)\phi - {\rm{j}}(M - 2){\omega _k}}}{]^{\rm{T}}}} \end{array} $ | (10) |
| $ \mathit{\boldsymbol{D}}({\theta _k}) = {\rm{diag}}\left\{ {{{\rm{e}}^{{\rm{j2}}L{\omega _k}}},{{\rm{e}}^{{\rm{j2}}(L - 1){\omega _k}}} \cdots ,{{\rm{e}}^{{\rm{j2}}(1 - L){\omega _k}}}} \right\} $ | (11) |
因此,当θ=θk时,矩阵JAD22-D(θk)AD11的第k和k+K列为零.
由于RD=RDH,所以RD为Hermitian矩阵,对RD进行特征值分解:
| $ {\mathit{\boldsymbol{R}}_D} = {\mathit{\boldsymbol{U}}_S}{\mathit{\boldsymbol{V}}_S}\mathit{\boldsymbol{U}}_S^{\rm{H}} + {\mathit{\boldsymbol{U}}_n}{\mathit{\boldsymbol{V}}_n}\mathit{\boldsymbol{U}}_n^{\rm{H}} $ | (12) |
其中VS∈R2K×2K为由2K个非零特征值组成的对角矩阵.由式(3)可知,这2K个非零特征值包含K个正特征值和K个负特征值,US∈RM×2K为信号子空间,Un∈RM×(M-2K)为噪声子空间,Vn∈R(M-2K)×(M-2K)为由M-2K个零特征值组成的对角矩阵.与式(6)相似,将信号子空间US的行以[2L, 1]与[1,2L]分块处理:
| $ {\mathit{\boldsymbol{U}}_S} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{U}}_{S11}}}\\ {{\mathit{\boldsymbol{U}}_{S12}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{U}}_{S21}}}\\ {{\mathit{\boldsymbol{U}}_{S22}}} \end{array}} \right] $ | (13) |
依据ESPRIT-Like算法原理,即存在一个2K×2K维满秩矩阵T,使得US11=AD11T和US22=AD22T,构造对角矩阵Ψ(θ):
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}(\theta ) = {\rm{diag}}\left\{ {{{\rm{e}}^{{\rm{j2}}L\omega }},{{\rm{e}}^{{\rm{j2}}(L - 1)\omega }} \cdots ,{{\rm{e}}^{{\rm{j2}}(1 - L)\omega }}} \right\} $ | (14) |
则有
| $ \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{U}}_{S22}} - \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}(\theta ){\mathit{\boldsymbol{U}}_{S11}} = (\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{A}}_{D22}} - \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}(\theta ){\mathit{\boldsymbol{A}}_{D11}})\mathit{\boldsymbol{T}} $ | (15) |
同理,当θ=θk时,矩阵JUS22-Ψ(θk)US11的第k和k+K列为零.
3 稀疏表示模型基于第2节分析,结合稀疏重构思想,将所估计的角度区间进行均匀网格划分为Θ=[θ1,θ2, …,θN],N为网格划分数,构建矩阵G:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}} = [ {\rm{vec }}(\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}({{\bar \theta }_1}){\mathit{\boldsymbol{U}}_{S11}}), {\rm{vec }}(\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}({{\bar \theta }_1}){\mathit{\boldsymbol{U}}_{S11}}),}\\ { \cdots , {\rm{vec }}(\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}({{\bar \theta }_N}){\mathit{\boldsymbol{U}}_{S11}})]} \end{array} $ | (16) |
由稀疏重构理论可知,稀疏信号可通过l0范数优化问题求解:
| $ {\rm{min}}{\left\| {{\kern 1pt} \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{p}}_N}{\kern 1pt} } \right\|_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\left\| {{\kern 1pt} {\rm{vec}} (\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{U}}_{S22}}) - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{p}}_N}{\kern 1pt} } \right\|_2} < \varepsilon $ | (17) |
式(17)是一个NP-hard问题,无法求解,因此将l0范数优化问题转化为无约束l1范数凸优化问题求解[10]:
| $ {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {{{\left\| {{\kern 1pt} {\rm{vec}} (\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{U}}_{S22}}) - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{p}}_N}{\kern 1pt} } \right\|}_2} + {{\left\| {{\kern 1pt} \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{p}}_N}{\kern 1pt} } \right\|}_1}} \right\} $ | (18) |
其中:pN=[p1, p2, …, pN],当角度θn=θk时,元素pn非零;否则pn为零,因此不存在对称伪峰,W为权函数,权函数表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{W}} = {\rm{diag}} \{ {\rm{det}} ({\mathit{\boldsymbol{C}}^{\rm{H}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{U}}_{S22}} - {\mathit{\boldsymbol{C}}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}({{\bar \theta }_1}){\mathit{\boldsymbol{U}}_{S11}}), \cdots ,\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{det}} ({\mathit{\boldsymbol{C}}^{\rm{H}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{U}}_{S22}} - {\mathit{\boldsymbol{C}}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}({{\bar \theta }_N}){\mathit{\boldsymbol{U}}_{S11}})} \right\} \end{array} $ | (19) |
其中C为任意的2L×2K维满秩矩阵.得到权函数后,利用CVX工具箱对式(18)求解得到稀疏向量pN,并寻找其中非零元素即可得到DOA估计值.
4 算法分析 4.1 信源过载能力对于M个阵元,K个入射信号的信号模型,NCME算法将非平稳噪声协方差矩阵分块成3个矩阵依次求解,因此需满足M≥3K. RTM算法在测量非平稳噪声矩阵时,要使信号协方差矩阵满足低秩条件,因此也需要满足M≥3K.而GCD算法与本文算法只是利用协方差差分矩阵抑制非平稳噪声的影响,因此只需满足M≥2K+1.综上可知,相比于RTM算法和NCME算法,本文算法的信源过载能力更优.
4.2 算法复杂度GCD算法与NCME算法利用传统MUSIC算法进行DOA估计,计算复杂度与MUSIC算法相同,为O(M3). RTM算法需解半定规划问题,计算复杂度为O(M3.5)[8].本文算法首先对差分矩阵RD进行特征值分解,计算复杂度为O(M3);其次构造N个权值计算复杂度为O(4L2N);最后利用CVX包求解式(18),计算复杂度为O(N3).因此本文计算复杂度为O(M3+4L2N+N3),一般情况下N≫M,计算复杂度可化简为O(N3). l1-SVD算法计算复杂度为O(K3N3)[10].综上可知,较之GCD算法、NCME算法与RTM算法,本文算法计算复杂度较高.主要原因是前3种算法是利用子空间算法完成DOA估计,而本文算法是利用稀疏重构完成DOA估计,但较之l1-SVD算法,本文算法的计算复杂度较低.
5 仿真分析为验证本文算法DOA估计性能,选取GCD算法、NCME算法、RTM算法与l1-SVD算法进行对比.仿真采用9个阵元的均匀线阵,阵元间距均为d=λ/2,ϕ=5,空间非平稳噪声协方差矩阵Q=σn2×diag{1, 5, 10, 2, 15, 0.1, 7, 18, 1},σn2为噪声功率,信噪比定义为10lg(σs2/σn2),σs2为信号功率.网格划分范围为(-90°, 90°),划分间隔为1°.定义均方根误差为
| $ \sqrt {\frac{1}{{{N_R}K}}\sum\limits_{k = 1}^K {\sum\limits_{r = 1}^{{N_R}} {{{(\hat \theta _k^r - {\theta _k})}^2}} } } $ |
其中:
仿真1 为验证本文算法的有效性,假设2个非相干的远场窄带信号分别以-20°和40°方向入射到阵列上,信噪比为10dB,快拍数为200,仿真结果如图 1所示.分析可知,l1-SVD算法无法准确进行DOA估计,GCD算法会出现对称伪峰,而NCME算法、RTM算法与本文算法能准确地进行DOA估计,表明本文算法解决了传统稀疏重构算法在非平稳噪声下失效的问题,并且消除了GCD算法带来的对称伪峰.

|
图 1 5种算法定位结果 |
仿真2 为验证本文算法的分辨率,假设2个非相干的远场窄带信号分别以20°、25°方向入射到阵列上,信噪比为-5dB,快拍数为200,仿真结果如图 2所示.分析可知,l1-SVD算法仍然无法准确进行DOA估计;GCD算法、NCME算法与RTM算法出现频谱混叠现象,无法分辨出20°和25°两个信源目标;本文算法能很好地分辨出这2个信源目标,表明其在低信噪比情况下具有较高的分辨率.
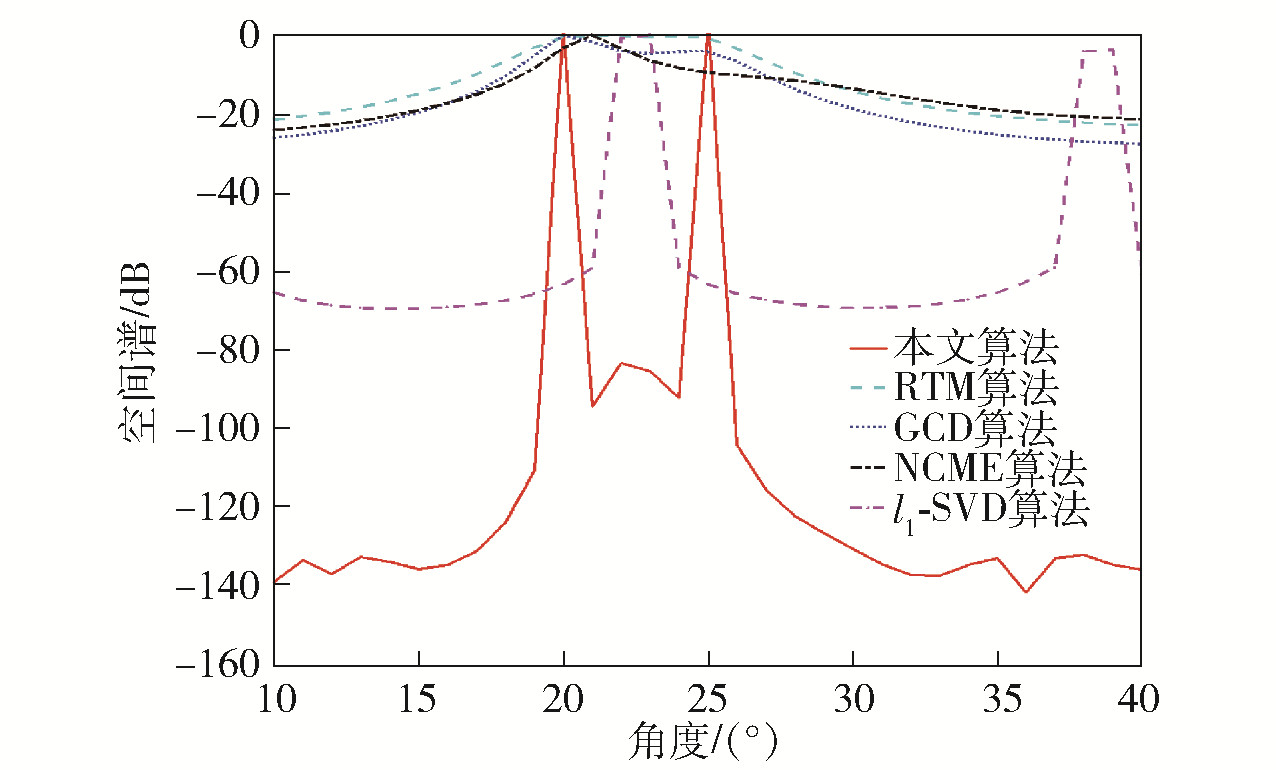
|
图 2 低信噪比且声源相距较近时定位结果 |
仿真3 为验证本文算法在不同信噪比下的估计性能,假设2个非相干远场窄带信号分别以30°、50°方向入射到阵列上,信噪比变化范围为[-10, 10]dB,变化间隔为2dB,快拍数为200,仿真结果如图 3所示.

|
图 3 RMSE随信噪比变化曲线 |
分析可知,4种算法均方根误差均随信噪比的增大而减小,在低信噪比情况下,本文算法的均方根误差始终低于其余3种算法,这表明本文算法具有较好的角度估计精度.
仿真4 为比较本文算法在不同快拍数下的估计性能,假设2个非相干远场窄带信号,分别以30°、50°方向入射到阵列上,信噪比为-5dB,快拍数变化范围为[50, 500],变化间隔为50,仿真结果如图 4所示.分析可知,4种算法的均方根误差均随快拍数的增大而降低,然而本文算法的均方根误差始终低于其他3种算法,表明本文算法的DOA估计性能受快拍数影响较小,在不同快拍数情况下均具有较高的估计精度.

|
图 4 RMSE随T变化曲线 |
仿真5 为验证本文算法在不同非平稳噪声协方差矩阵下的有效性,设置3个噪声协方差矩阵:Q1=Q,Q2=σn2diag{5, 1, 20, 1.5, 0.1, 7, 2.3, 2, 4}、Q3=σn2diag{12, 0.4, 2, 1, 5, 3.2, 6, 7, 2.3},其他仿真参数的设置如仿真2,仿真结果如图 5所示.分析可知,在低信噪比且不同的噪声协方差条件下,本文算法均可有效地识别2个目标声源,表明本文算法具有较好的噪声鲁棒性能.

|
图 5 本文算法在不同非平稳噪声下的定位结果 |
提出了非平稳噪声下基于稀疏表示的DOA估计算法,该算法不但利用类协方差差分抑制了非平稳噪声的影响,而且基于ESPRIT-Like算法原理构造稀疏表示模型并消除了协方差差分技术带来的对称伪峰.所提算法解决了传统稀疏重构定位算法无法适用于非平稳噪声环境下的问题,较之传统GCD算法、NCME算法和RTM算法,虽然计算复杂度较高,然而信源过载能力较强;同时,仿真结果表明,所提算法具有较高的分辨率与较好的DOA估计性能.
| [1] |
吴晨曦, 张旻, 王可人. 非均匀噪声背景下的欠定DOA估计方法[J]. 系统工程与电子技术, 2018, 40(3): 498-503. Wu Chenxi, Zhang Min, Wang Keren. Underdetermined direction of arrival estimation with nonuniform noise[J]. Systems Engineering and Electronics, 2018, 40(3): 498-503. |
| [2] |
Liu Aijun, Li Fen, Li Bo, et al. Spatial polarimetric time-frequency distribution based DOA estimation:combining ESPRIT with MUSIC[J]. EURASIP Journal on Wireless Communications and Networking, 2018, 51. |
| [3] |
Liu Song, Zhang Gang, Weng Mingjiang, et al. Unified ESPRIT spatial spectrum for direction-of-arrival estimation with an arbitrary sparse array[C]//2016 IEEE 13th International Conference on Signal Processing (ICSP). New York: IEEE Press, 2016: 457-461.
|
| [4] |
陈明建, 胡振彪, 黄中瑞. 空间非平稳噪声下的宽带DOA估计算法[J]. 现代雷达, 2018, 40(1): 36-42. Chen Mingjian, Hu Zhenbiao, Huang Zhongrui. Direction of arrival estimation of wideband signals with sensor arrays in spatial non-stationary noise[J]. Modern Radar, 2018, 40(1): 36-42. |
| [5] |
Qi Chongying, Chen Zhijie, Wang Yongliang, et al. DOA estimation for coherent sources in unknown nonuniform noise fields[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1195-1204. DOI:10.1109/TAES.2007.4383611 |
| [6] |
吴云韬, 廖桂生, 张光斌. 空间非平稳噪声环境下的DOA估计新算法[J]. 西安电子科技大学学报, 2003, 30(1): 51-54. Wu Yuntao, Liao Guisheng, Zhang Guangbin. A novel method for estimating DOA in the presence of spatially nonstationary noise fields[J]. Journal of Xidian University, 2003, 30(1): 51-54. DOI:10.3969/j.issn.1001-2400.2003.01.012 |
| [7] |
汪弟杰, 王敏. 一种加性色噪声下的DOA估计新算法[J]. 广东通信技术, 2016, 36(1): 28-31. Wang Dijie, Wang Min. A noval DOA estimation algorithms in additive colored noise[J]. Guangdong Communication Technology, 2016, 36(1): 28-31. DOI:10.3969/j.issn.1006-6403.2016.01.007 |
| [8] |
Liao Bin, Huang Lei, Guo Chongtao, et al. New approaches to direction-of-arrival estimation with sensor arrays in unknown nonuniform noise[J]. IEEE Sensors Journal, 2016, 16(24): 8982-8989. DOI:10.1109/JSEN.2016.2621057 |
| [9] |
王洪雁, 房云飞, 裴炳南. 利用空间平滑的协方差秩最小化DOA估计方法[J]. 西安电子科技大学学报, 2018, 45(5): 128-135. Wang Hongyan, Fang Yunfei, Pei Bingnan. Method for estimation of covariance rank minimization DOA by exploiting spatial smoothing[J]. Journal of Xidian University, 2018, 45(5): 128-135. DOI:10.3969/j.issn.1001-2400.2018.05.021 |
| [10] |
Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022. DOI:10.1109/TSP.2005.850882 |
| [11] |
Zhao Wenqiang, Li Gang, Zheng Chundi, et al. Capon cepstrum weighted l2, 1 minimization for wideband DOA estimation with sonar arrays[C]//OCEANS 2016-Shanghai. New York: IEEE Press, 2016: 1-4.
|
| [12] |
赵季红, 马兆恬, 曲桦, 等. 基于加权l范数稀疏信号重建的DOA估计[J]. 北京邮电大学学报, 2016, 39(5): 33-36, 66. Zhao Jihong, Ma Zhaotian, Qu Hua, et al. DOA estimation based on sparse signal recovery utilizing weight l Norm[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(5): 33-36, 66. |
| [13] |
Liu Guohong, Sun Xiaoying. Two-stage matrix differencing algorithm for mixed far-field and near-field sources classification and localization[J]. IEEE Sensors Journal, 2014, 14(6): 1957-1965. DOI:10.1109/JSEN.2014.2307060 |
| [14] |
刘国红.远近场混合源定位参量估计算法研究[D].长春: 吉林大学, 2015.
|


