根据实际中的纠缠微波信号生成电路设计元器件参数,以提高产生纠缠微波信号的纠缠度,提出了纠缠微波信号的量子仿真模型.根据电磁场的量子化,将电场强度用可观测的物理量——正交分量来表示,把纠缠微波信号的表达式代入电场强度的表达式中,得到电场强度与输入角频率、压缩参量以及噪声涨落之间的关系.以正态分布的随机数作为噪声涨落的输入,对比分析了在不同压缩参量下电场强度正交分量随时间变化的关系以及在相同压缩参量下输入分别为真空态和压缩态时的情况.结果表明,该纠缠微波信号仿真模型所表示的电场强度能够反映出正交分量之间的正反关联特性,且关联度与压缩参量成正比,输入压缩度越高,关联度越高,与实验结论相吻合.
In order to facilitate the design of component parameters based on actual generating circuits of entangled microwave signals and improve the entanglement degree of entangled microwave signals, a quantum simulation model of entangled microwave signals is proposed. Firstly, according to the quantization of electromagnetic field, the electric-field intensity of entangled microwave signals is represented by the observable physical quantity-quadrature components. Then, the relation among the electric-field intensity and the input angular frequency, the squeezed parameter and the noise fluctuation is obtained. Subsequently, the random numbers with Gaussian distribution are used as the input of vacuum state or squeezed state to analyze the changing of the exacting quadrature components with time. It is shown that the quantum simulation model of entangled microwave signals can reflect the positive and negative correlation characteristics of quadrature components. The correlation degree is proportional to the squeezed parameter.
纠缠是量子力学中的一种特殊“资源”,它反映了2个或2个以上子系统之间不可区分的非定域关联特性,即使将它们空间分离,对一个子系统的观测也势必影响其他子系统的测量结果.如今,以量子通信、量子计算为代表的量子信息科学迅速发展,人们对于纠缠的理解和应用也逐步加深.然而,目前绝大多数研究都是基于光学频段的量子特性.相比光学频段而言,对微波频段量子特性的研究则起步较晚,这是由它本身的物理性质决定的.近年来,随着超导量子微波电路的出现,实验中已发现并验证了微波频段的纠缠特性,产生的信号称为纠缠微波信号.以约瑟夫森结为核心的超导电路是产生纠缠微波信号的核心器件. 2012年,Menzel小组利用约瑟夫森参量放大器(JPA, Josephson parameter amplifier)产生的单模压缩态与50 Ω负载产生的真空态在微波分束器中混合,制备了空间分离的频率简并式连续变量纠缠微波信号[1].同年,Flurin小组利用泵浦腔驱动约瑟夫森混频器(JM, Josephson mixer),制备了空间分离的频率非简并式纠缠微波信号[2].纠缠微波信号是一种连续变量纠缠,它反映的是微波场正交分量之间的非定域性关联.纠缠微波信号在连续变量量子信息处理以及大尺度动态空间环境中有重要的应用前景[3].
由于纠缠微波信号的电路要求非常精细,且目前生成纠缠微波信号的纯度还不够高,所以有必要建立纠缠微波信号的量子仿真模型,利用该模型表示出电路中各个元件参数对生成信号纠缠度的影响,以方便进行电路的设计和调试. Massar等[4]证明量子纠缠可以通过经典的方式模拟;Andrei等[5]提出了量子信道能够通过经典高斯信号的线性变换来表示.这些研究从理论上证明了非经典的纠缠信号可以利用经典的手段来仿真,为研究工作提供了理论基础,但没有给出实现方法,更关注的是具体实施过程,即从电路参数入手,给出宏观可见的信号时域波形.利用量子仿真模型可模拟高纯度的纠缠信号,从而方便进行后续传播检测及应用方面的理论研究,为早日将纠缠微波信号投入实际应用提供足够的支持[6-7].
1 纠缠微波信号的表示Flurin等[2]利用泵浦腔驱动约瑟夫森混频器制备了纠缠微波信号,处于纠缠状态的2路信号分别表示为
| $ \begin{array}{*{20}{l}} {{{\hat S}_1}(t) = \sqrt G \hat a(t) + {{\rm{e}}^{{\rm{i}}\varphi }}\sqrt {G - 1} {{\hat b}^ + }(t)}\\ {{{\hat S}_2}(t) = \sqrt G \hat b(t) + {{\rm{e}}^{{\rm{i}}\varphi }}\sqrt {G - 1} {{\hat a}^ + }(t)} \end{array} $ | (1) |
其中
Flurin等[2]给出了放大增益的表达式,其中:
| $ {\sqrt G = \frac{{{\kappa _a}{\kappa _b} + 4{\chi ^2}|P{|^2}}}{{{\kappa _a}{\kappa _b} - 4{\chi ^2}|P{|^2}}}} $ | (2) |
| $ {\sqrt {G - 1} = \frac{{4\chi |P|\sqrt {{\kappa _a}{\kappa _b}} }}{{{\kappa _a}{\kappa _b} - 4{\chi ^2}|P{|^2}}}} $ | (3) |
κa、κb为信号的带宽,χ为二阶非线性系数,|P|为泵浦信号的幅度.当然,在生成纠缠微波信号的不同电路中,参量放大的增益大小是不同的,它与具体的元器件参数有关,但始终都满足形如
令
| $ \begin{array}{*{20}{l}} {{{\hat S}_1}(t) = {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat a(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat b}^ + }(t)}\\ {{{\hat S}_2}(t) = {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat b(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat a}^ + }(t)} \end{array} $ | (4) |
这正是双模压缩真空态的表示.实际中,纠缠微波信号的产生过程也正是双模压缩真空态的产生过程.
2 量子仿真理论模型对纠缠微波信号进行量子仿真,针对的对象是信号的电场强度.在量子力学中,电场强度为[8]
| $ \hat E(t) = \sum\limits_k {\sqrt {\frac{{\hbar {\omega _k}}}{{2{\varepsilon _0}}}} } ({\hat a_k}(t){{\rm{e}}^{ - {\rm{i}}{\omega _k}t}} + \hat a_k^ + (t){{\rm{e}}^{{\rm{i}}{\omega _k}t}}) $ | (5) |
其中:k为任意常数,表示模式的连续性,
| $ \hat E(t) = \sum\limits_k {\sqrt {\frac{{2\hbar {\omega _k}}}{{{\varepsilon _0}}}} } ({\hat X_k}(t){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ({\omega _k}t) + {\hat Y_k}(t){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ({\omega _k}t)) $ | (6) |
其中
| $ \begin{array}{*{20}{l}} {{{\hat X}_k}(t) = \frac{1}{2}({{\hat a}_k}(t) + \hat a_k^ + (t))}\\ {{{\hat Y}_k}(t) = \frac{1}{{2i}}({{\hat a}_k}(t) - \hat a_k^ + (t))} \end{array} $ |
| $ \hat E(t) \leftrightarrow E(t),{\hat X_k}(t) \leftrightarrow {X_k}(t),{\hat Y_k}(t) \leftrightarrow {Y_k}(t) $ |
对纠缠微波信号而言,角频率是相同的,所以令ωk=ω,
| $ \begin{array}{*{20}{l}} {{{\hat E}_1}(t) = \sqrt {\frac{{2\hbar \omega }}{{{\varepsilon _0}}}} ({{\hat X}_1}(t){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t + {{\hat Y}_1}(t){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t)}\\ {{{\hat E}_2}(t) = \sqrt {\frac{{2\hbar \omega }}{{{\varepsilon _0}}}} ({{\hat X}_2}(t){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t + {{\hat Y}_2}(t){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t)} \end{array} $ | (7) |
根据式(4),首先得到电场的正交分量分别为
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat X}_1}(t) = \frac{1}{2}({{\hat S}_1}(t) + \hat S_1^ + (t)) = }\\ {\frac{1}{2}({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat a(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat b}^ + }(t) + }\\ {{\kern 1pt} {\kern 1pt} {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat a}^ + }(t) + {{\rm{e}}^{ - {\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat b(t)) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)(\hat a(t) + {{\hat a}^ + }(t)) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)({{\rm{e}}^{ - {\rm{i}}\varphi }}\hat b(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{{\hat b}^ + }(t))} \end{array} $ | (8) |
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat Y}_1}(t) = \frac{1}{{2{\rm{i}}}}({{\hat S}_1}(t) - \hat S_1^ + (t)) = }\\ {\frac{1}{{2{\rm{i}}}}({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat a(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat b}^ + }(t) - }\\ {{\kern 1pt} {\kern 1pt} {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat a}^ + }(t) - {{\rm{e}}^{ - {\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat b(t)) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{2{\rm{i}}}}{\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)(\hat a(t) - {{\hat a}^ + }(t)) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{2{\rm{i}}}}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)({{\rm{e}}^{ - {\rm{i}}\varphi }}\hat b(t) - {{\rm{e}}^{{\rm{i}}\varphi }}{{\hat b}^ + }(t))} \end{array} $ | (9) |
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat X}_2}(t) = \frac{1}{2}({{\hat S}_2}(t) + \hat S_2^ + (t)) = }\\ {\frac{1}{2}({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat b(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat a}^ + }(t) - }\\ {{\kern 1pt} {\kern 1pt} {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat b}^ + }(t) + {{\rm{e}}^{ - {\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat a(t)) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)(\hat b(t) + {{\hat b}^ + }(t)) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)({{\rm{e}}^{ - {\rm{i}}\varphi }}\hat a(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{{\hat a}^ + }(t))} \end{array} $ | (10) |
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat Y}_2}(t) = \frac{1}{{2{\rm{i}}}}({{\hat S}_2}(t) - \hat S_2^ + (t)) = }\\ {\frac{1}{{2{\rm{i}}}}({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat b(t) + {{\rm{e}}^{{\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat a}^ + }(t) - }\\ {{\kern 1pt} {\kern 1pt} {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat b}^ + }(t) - {{\rm{e}}^{ - {\rm{i}}\varphi }}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\hat a(t)) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{2{\rm{i}}}}{\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)(\hat b(t) - {{\hat b}^ + }(t)) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{2{\rm{i}}}}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)({{\rm{e}}^{ - {\rm{i}}\varphi }}\hat a(t) - {{\rm{e}}^{{\rm{i}}\varphi }}{{\hat a}^ + }(t))} \end{array} $ | (11) |
令φ=0,则
| $ {{{\hat X}_1}(t) = {\rm{cosh}}(r){{\hat X}_a}(t) + {\rm{sinh}}(r){{\hat X}_b}(t)} $ | (12) |
| $ {{{\hat X}_2}(t) = {\rm{cosh}}(r){{\hat X}_b}(t) + {\rm{sinh}}(r){{\hat X}_a}(t)} $ | (13) |
| $ {{{\hat Y}_1}(t) = {\rm{cosh}}(r){{\hat Y}_a}(t) - {\rm{sinh}}(r){{\hat Y}_b}(t)} $ | (14) |
| $ {{{\hat Y}_2}(t) = {\rm{cosh}}(r){{\hat Y}_b}(t) - {\rm{sinh}}(r){{\hat Y}_a}(t)} $ | (15) |
其中:
将式(12)~(15)代入式(7)中,得到
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{{\hat E}_1}(t) = }\\ {\sqrt {\frac{{2\hbar \omega }}{{{\varepsilon _0}}}} [({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat X}_a}(t) + {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat X}_b}(t)){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t + }\\ {({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat Y}_a}(t) - {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat Y}_b}(t)){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t]} \end{array}\\ \begin{array}{*{20}{c}} {{{\hat E}_2}(t) = }\\ {\sqrt {\frac{{2\hbar \omega }}{{{\varepsilon _0}}}} [({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat X}_b}(t) + {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat X}_a}(t)){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t + }\\ {({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat Y}_b}(t) - {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){{\hat Y}_a}(t)){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t]} \end{array} \end{array} $ | (16) |
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{E_1}(t) = }\\ {K\sqrt \omega [({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){X_a}(t) + {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){X_b}(t)){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t + }\\ {({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){Y_a}(t) - {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){Y_b}(t)){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t]} \end{array}\\ \begin{array}{*{20}{c}} {{E_2}(t) = }\\ {K\sqrt \omega [({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){X_b}(t) + {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){X_a}(t)){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t + }\\ {({\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){Y_b}(t) - {\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r){Y_a}(t)){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t]} \end{array} \end{array} $ | (17) |
其中:
笔者研究的是微波频段的纠缠信号,所以ω处于微波波段,这里选择ω=2π×5 GHz.若要实现输入的信号a(t)与b(t)为真空态,则可以令a(t)与b(t)的4个正交分量Xa(t)、Ya(t)与Xb(t)、Yb(t)分别取(0, 1)之间的随机数,象征着真空涨落圆的大小为单位圆.又由于在相空间描述真空态正交分量的边缘概率密度函数为正态分布,因此,仿真中输入的4个正交分量取以正态分布变化的(0, 1)之间的随机数.
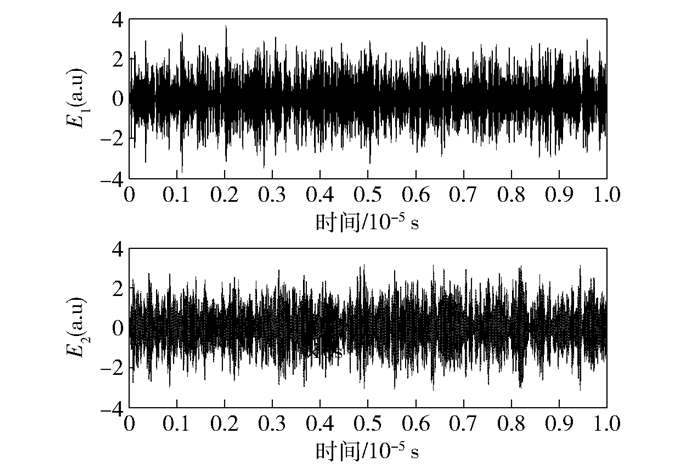
首先分析当压缩参量r取不同的值时,仿真得到的结果. 图 1所示为r=0时,电场强度大小随时间变化的曲线.
|
图 1 r=0时,电场强度大小随时间的变化 |
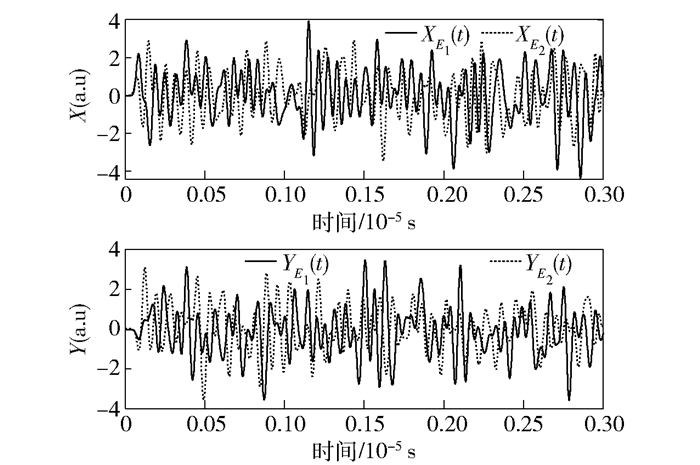
从图 1中可以看出,输出电场强度E1(t)和E2(t)的大小是随时间随机变化的.理想的纠缠应表现为信号正交分量之间的正反关联.为了反映这一特征,根据常采用的零拍探测(Homodyne detection)方法,在获得E1(t)和E2(t)之后,需要与频率为ω的本振信号相乘,去掉载波,以提取信号的正交分量信息. 图 2所示为提取的正交分量XE1(t)、XE2(t)、YE1(t)、YE2(t)大小随时间变化的曲线,这里滤波器的带宽为20 MHz.
|
图 2 r=0时,2路信号正交分量随时间的变化 |
从图 2中可以看出,2路信号的正交分量都是随着时间随机变化的,没有任何关联存在.
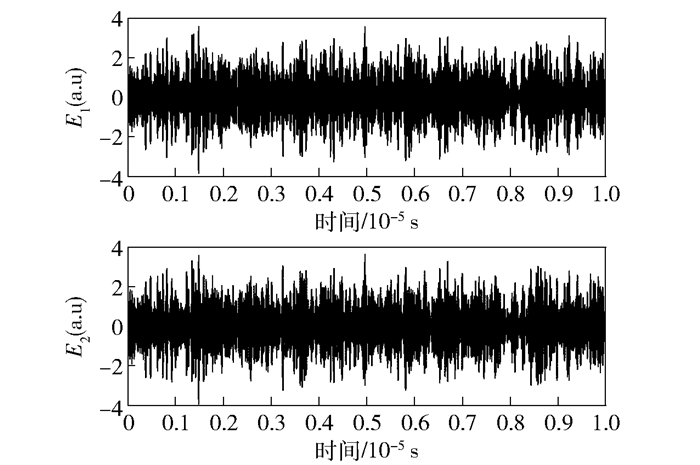
r=1时电场强度大小随时间变化曲线如图 3所示.
|
图 3 r=1时,电场强度大小随时间的变化 |
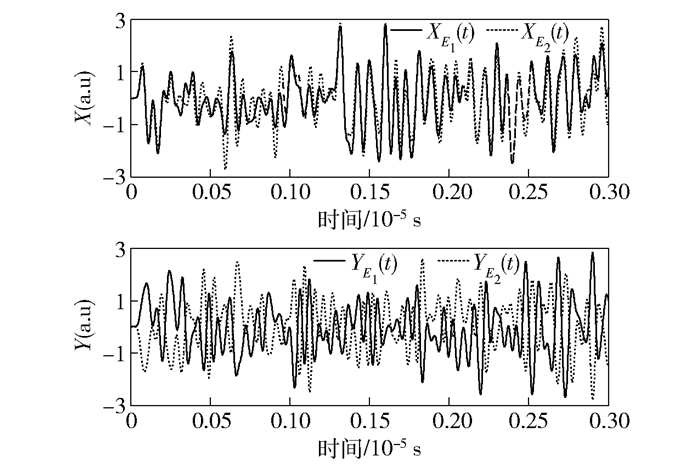
从图 3可以看出,电场强度的大小仍然是随时间随机变化的.与图 1相比,直观上的感觉是幅度上下波动更为剧烈.再次提取它的正交分量信息,如图 4所示.
|
图 4 r=1时,2路信号正交分量随时间的变化 |
从图 4中可以明显看出,2路信号同方向正交分量之间存在着相似的变化趋势,其中X方向表现为正关联,Y方向表现为反关联,但这种关联并不是完全一致的,还存在着一些偏差.
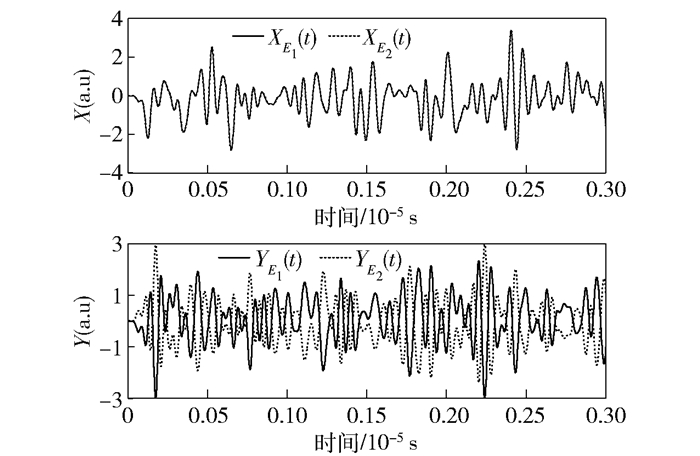
r=3时的结果如图 5所示.
|
图 5 r=3时,2路信号正交分量随时间的变化 |
从图 5中可以看出,2路信号正交分量之间的变化趋势已趋近于完全一致,X方向几乎达到了理想的正关联,同样,Y方向几乎达到了理想的反关联.
随着r的继续增大,2路信号之间的关联度越来越高,直到r→+∞时,将达到理想纠缠所表现的正交分量正反关联特性.
从理论上说,随着r的增大,cosh (r)≈sinh (r).因此,简化式(17),可以得到
| $ \begin{array}{l} {E_1}(t) = K\sqrt \omega {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\left[ {\left( {{X_a}(t) + {X_b}(t)} \right){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t + } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{Y_a}(t) - {Y_b}(t)} \right){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t} \right]\\ {E_2}(t) = K\sqrt \omega {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (r)\left[ {\left( {{X_a}(t) + {X_b}(t)} \right){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{Y_a}(t) - {Y_b}(t)} \right){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \omega t} \right] \end{array} $ | (18) |
这恰恰反映出了提取正交分量之间的正反关联特性.
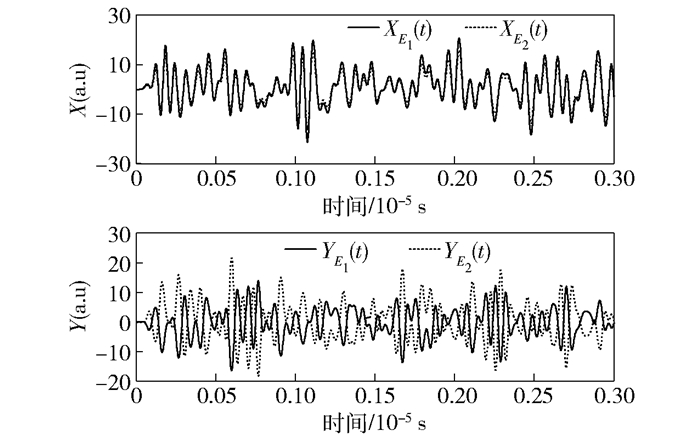
上述分析中,输入的4个正交分量分别取(0, 1)之间的随机数,象征着涨落圆的大小是单位圆.这一过程就相当于真空态在一定条件作用下,生成为双模压缩真空态的过程.另外,还可以考虑输入为2个单模压缩态时的情况.输入的涨落圆应为压缩的圆,正交分量的取值范围相比之前有变化.具体的做法是Xa(t)取(0, es)之间的随机数,Ya(t)取(0, e-s)之间的随机数(s≠0).同理,Xb(t)取(0, e-s)之间的随机数,Yb(t)取(0, es)之间的随机数.据此,r=1,s=5时的结果如图 6所示.
|
图 6 r=1, s=5时,2路信号正交分量随时间的变化 |
与图 4进行对比可以发现,2路信号同方向正交分量之间的关联度增加,并且伴随着信号的幅值增加.因此,当2个输入为单模压缩态时,得到的2路信号之间的关联度要比输入为真空态时的关联度要高.这一过程相当于在已有压缩的基础上继续进行压缩,生成纠缠信号的纠缠度将会提高.结果也同时证明了该仿真方法的合理性和可行性.
4 结束语建立了纠缠微波信号的量子仿真模型,分析了输入为真空态时,不同压缩参量下模型所表示的2路信号正交分量之间的关系以及对比了相同压缩参量下,输入分别为真空态和压缩态时的结果.仿真分析结果表明,提出的纠缠微波信号量子仿真模型结果与实验中测量的结果基本一致,能够反映出2体纠缠态的单路随机性以及双路正反关联性.利用该量子仿真模型可直接进行信号的模拟和计算.与实际的纠缠微波信号相比,唯一的不同在于仿真中利用计算机输入的随机数是伪随机的,而纠缠微波信号的涨落是真随机的.但这并不影响实际电路中各元件参数与产生信号纠缠度之间的关系,仍然可利用该模型来设计具体电路参数值,提高产生纠缠微波信号的纠缠度,并进行传播检测和应用方面的理论研究.
| [1] |
Menzel E P, Candia R Di, Deppe F, et al. Path entanglement of continuous-variable quantum microwaves[J]. Phys Rev Lett, 2012, 109(25): 250502(4). |
| [2] |
Flurin E, Roch N, Mallet F, et al. Generating entangled microwave radiation over two transmission lines[J]. Phys Rev Lett, 2012, 109(18): 183901. DOI:10.1103/PhysRevLett.109.183901 |
| [3] |
李响, 吴德伟, 苗强, 等. 纠缠微波信号的特性及表示方法[J]. 物理学报, 2018, 67(24): 240301. Li Xiang, Wu Dewei, Miao Qiang, et al. Characteristics and expressions of entangled microwave signals[J]. Acta Phys Sin, 2018, 67(24): 240301. DOI:10.7498/aps.67.20181595 |
| [4] |
Massar S, Bacon D, Cerf N J., et al. Classical simulation of quantum entanglement without local hidden variables[J]. Phys Rev A, 2001, 63(5): 052305. |
| [5] |
Andrei K, Masanori O, Naboru W. Classical signal model for quantum channels[J]. J Russ Laser Res, 2010, 31(5): 462-468. DOI:10.1007/s10946-010-9167-x |
| [6] |
Barzanjeh S, Guha S, Weedbrook C, et al. Microwave quantum illumination[J]. Phys Rev Lett, 2015, 114(8): 080503. DOI:10.1103/PhysRevLett.114.080503 |
| [7] |
Li X, Wu D W, Miao Q, et al. A navigation ranging scheme with true random entangled microwave signals[J]. IEEE Photon J, 2018, 10(6): 6101107. |
| [8] |
张智明. 量子光学[M]. 北京: 科学出版社, 2015.
|



