2. 国网信息通信产业集团有限公司, 北京 102211
机会移动社群网络易受到不良节点干扰而导致正常通信中断,现有研究方法普遍存在忽略不良行为差异性,为此,提出了基于狄利克雷分布的可信路由转发机制.利用消息传递过程判断节点的可信度,提出应对干扰的路由转发机制.实验结果表明,在受到不良节点干扰的条件下,该机制能够准确评估节点,同时在保持低传输成本的情况下,传输成功率比传统方法提高了5%~10%.
2. State Grid Information and Telecommunication Group Company Limited, Beijing 102211, China
The opportunistic mobile social network is vulnerable to the interruption of normal communication due to the interference of bad nodes. Existing research methods generally have the problem of neglecting the difference of bad behavior. The article proposes a trusted routing and forwarding mechanism based on Dirichlet distribution. Firstly, the message passing process is used to judge the credibility of the node, and then the routing and forwarding mechanism for dealing with interference is proposed. Experiment shows that the mechanism can accurately evaluate nodes under the condition of poor node interference, and the transmission success rate is 5%~10% higher than the traditional method while keeping the transmission cost low.
随着网络边缘侧的高速发展,越来越多的边缘业务通过终端协同实现,如智慧校园、移动自组织网络[1]等.在机会移动社群网络中,存在终端受用户主观因素约束而引起不良行为的现象,破坏了机会移动社群网络的公平秩序,成为亟待解决的问题.
规避不良节点逐渐引起学者的关注[2],一般采用直接与间接的方式进行评估.其中,Chen等[3]提出了以密钥配对来确认节点身份,以待评估节点历史数据确认节点行为;Yao等[4]提出了名为基于社交相似性的可信路由方法(TRSS, the trust routing scheme based on social similarity),利用社交相似性加快身份认证,通过交互评估结果完成间接评估.但是,上述方法均存在忽略不良行为差异性的问题,导致评估可能出现错误.基于狄利克雷分布的评估方法由Josang等[5]在社交网络中首次提出.随后,Li等[6]类比应用到移动自组网中,但并未对数据获取进行更深入地研究. Denko等[7]提出了记录服务情况,但未完全解决忽略不良行为差异性的问题.
笔者针对终端破坏机会移动社群网络公平秩序的问题,提出了基于狄利克雷分布的可信路由转发机制(TRFDD, trusted routing and forwarding mechanism based on Dirichlet distribution),其中包含关注不良行为差异性的直接与间接可信评估流程以及基于评估结果的路由转发算法,最后通过仿真对算法效果进行比对验证.
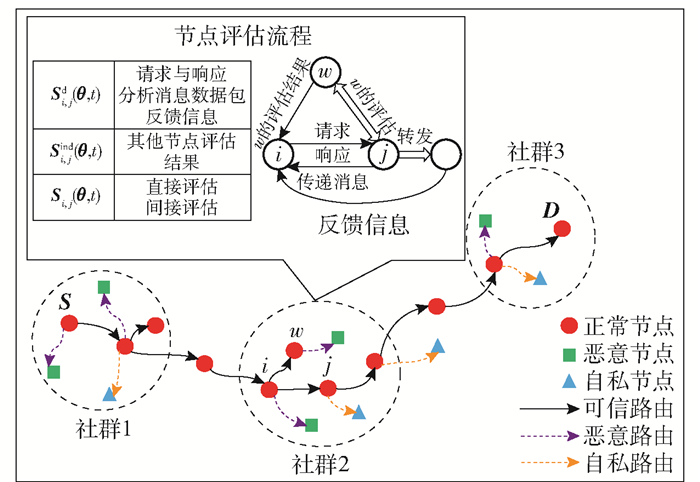
1 数学模型 1.1 问题描述在机会移动社群网络中,内容资源共享通过节点间机会接触实现,如图 1所示.不良节点的存在制约着机会移动社群网络正常秩序的建立.由于自私节点拒绝服务,易造成网络资源分配不公平.恶意节点丢弃数据包,诋毁其他节点导致通信质量下降,同时加大了网络负载,降低了通信效率.为避免自私与恶意行为,需采取评估方法进行应对.
|
图 1 机会移动社群网络路由选择示意图 |
以图 1中3个社群为例,源节点S处于社群1中,通过评估选择正常节点实现消息转发,最终传递到社群3中的目标D.如何设计可信节点评估方法和相应的路由转发算法成为研究的核心内容.
本研究旨在利用消息传递过程中获取的信息评估节点的可信程度.为此,定义每个节点通过分析请求与响应、消息数据包与反馈信息得到的节点i对节点j的直接评估结果向量为Si, jd(θ, t),通过获取邻居节点w的评估结果计算处理得到的间接评估结果向量,记为Si, jind(θ, t),二者相加得到描述节点最终可信程度的向量Si, j(θ, t),选择arg max Si, j(θ, t)为正常的节点作为转发的候选节点.对于自私节点,将其记录于观察名单中,并以flag位标记社交型自私节点.对于恶意节点,将其记录于黑名单中,根据评估结果以时间窗的方式定期更新2个名单.
1.2 问题模型节点i为选取可信节点,需要通过对候选节点j的直接评价Si, jd(θ, t)与其他节点w对j节点的间接评价Si, jind(θ, t)综合计算最终评价Si, j(θ, t).其中,t为当前所处时间窗;向量θ=[θ1, θ2, θ3]为节点的可信程度,并将其划分为正常、自私和恶意3类,分别用θ1、θ2和θ3表示.通过基于狄利克雷的概率分布模型计算,最终评估结果表示为
| $ {\mathit{\boldsymbol{S}}_{i,j}}(\mathit{\boldsymbol{\theta }},t) = \mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t) + \mathit{\boldsymbol{S}}_{i,j}^{{\rm{ind}}}(\mathit{\boldsymbol{\theta }},t) $ | (1) |
狄利克雷概率密度函数如下:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f({p_j}(\mathit{\boldsymbol{\theta }},t)|{\alpha _{i,j}}(\mathit{\boldsymbol{\theta }},t)) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\Gamma \left( {\sum\limits_{k = 1}^3 {{\alpha _{i,j}}} ({\theta _k},t)} \right)}}{{\prod\limits_{k = 1}^3 \Gamma ({\alpha _{i,j}}({\theta _k},t))}}\prod\limits_{k = 1}^3 {{p_j}} {({\theta _k},t)^{{\alpha _{i,j}}({\theta _k},t) - 1}}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{p_j}({\theta _1},t),{p_j}({\theta _2},t),{p_j}({\theta _3},t) \ge 0}\\ {\sum\limits_{k = 1}^3 {{p_j}} ({\theta _k},t) = 1}\\ {{\alpha _{i,j}}({\theta _1},t),{\alpha _{i,j}}({\theta _2},t),{\alpha _{i,j}}({\theta _3},t) > 0} \end{array}} \right. \end{array} $ | (2) |
直接评估利用通信过程获取的数据,计算狄利克雷概率期望:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}({\theta _k},t) = E({p_j}({\theta _k},t)|{\mathit{\boldsymbol{\alpha }}_{i,j}}(\mathit{\boldsymbol{\theta }},t)) = }\\ {\frac{{{\mathit{\boldsymbol{\alpha }}_{i,j}}({\theta _k},t)}}{{\sum\limits_{k = 1}^3 {{\mathit{\boldsymbol{\alpha }}_{i,j}}} ({\theta _k},t)}},k = 1,2,3} \end{array} $ | (3) |
其中:向量pj(θ, t)=[pj(θ1, t), pj(θ2, t), pj(θ3, t)]为节点j在当前时间窗内3种可信程度的概率;αi, j(θ, t)=[αi, j(θ1, t), αi, j(θ2, t), αi, j(θ3, t)]为节点i在当前时间窗内观测到的节点j出现3种类别行为的次数,αi, j(θk, t)表示为
| $ \begin{array}{*{20}{c}} {{\alpha _{i,j}}({\theta _k},t) = {\varphi _{i,j}}({\theta _k},t) + \sum\limits_{m = 1}^3 {{v_m}} \varepsilon _j^{{v_m}}({\theta _k},t),}\\ {k = 1,2,3} \end{array} $ | (4) |
其中:φi, j(θ, t)=[φi, j(θ1, t), φi, j(θ2, t), φi, j(θ3, t)]为描述当前时间窗初始时刻待评估节点可信程度的基础概率,满足
在t=0时,不同社交关系的节点具有不同的初始基础概率:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{\varphi }}_{i,j}}(\mathit{\boldsymbol{\theta }},0) = \\ \left\{ \begin{array}{l} \left( {\frac{2}{3},\frac{1}{6},\frac{1}{6}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{rel}} (i,j) = {\rm{ Friends}}\\ \left( {\frac{1}{2},\frac{1}{4},\frac{1}{4}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{rel}} (i,j) = {\rm{ Strangers}}\\ \left( {\frac{1}{3},\frac{1}{3},\frac{1}{3}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{rel}} (i,j) = {\rm{ Others }} \end{array} \right. \end{array} $ | (5) |
其中
| $ {\rm{Match}}(i,j) = \frac{{|{\mathit{\boldsymbol{F}}_i} \cap {\mathit{\boldsymbol{F}}_j}|}}{N} $ | (6) |
其中:向量F=[f1, f2, …, fN]为节点的N个社会属性,用于计算节点间的社交相似性,为相同属性数量与所有属性数量的比值.满足阈值条件th的节点记为Friends,不满足阈值条件的节点记为Strangers.对于间接接触到的节点记为Others.
基础概率随时间的更新如下,上一时间窗评估结果作为新时间窗的基础概率.
| $ {\mathit{\boldsymbol{\varphi }}_{i,j}}(\mathit{\boldsymbol{\theta }},t + \tau ) = {\mathit{\boldsymbol{S}}_{i,j}}(\mathit{\boldsymbol{\theta }},t) $ | (7) |
根据行为对评估的影响程度将对应行为的增长速率划分为半速、基本速率和二倍速,用向量υm=(υ1, υ2, υ3)表示,m代表速率等级;εjυm(θk, t)表示节点j在当前时间窗内的可信程度为θk、增长速率为υm的行为出现频数.直接评估的结果为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}({\theta _k},t) = E({p_j}({\theta _k},t)|{\mathit{\boldsymbol{\alpha }}_{i,j}}(\mathit{\boldsymbol{\theta }},t)) = }\\ {\frac{{{\varphi _{i,j}}({\theta _k},t) + \sum\limits_{m = 1}^3 {{v_m}} \varepsilon _j^{{v_m}}({\theta _k},t)}}{{1 + \sum\limits_{k = 1}^3 {\sum\limits_{m = 1}^3 {{v_m}} } \varepsilon _j^{{v_m}}({\theta _k},t)}},k = 1,2,3\quad } \end{array} $ | (8) |
间接评估利用其他节点w的直接评估信息,即
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}}_{i,j}^{{\rm{ind}}}(\mathit{\boldsymbol{\theta }},t) = }\\ {\sum\limits_{w = 1}^W \omega (\mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t),\mathit{\boldsymbol{S}}_{w,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t))\gamma (i,w)\mathit{\boldsymbol{S}}_{w,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t)} \end{array} $ | (9) |
其中:w代表与节点i、j均接触过的第三方节点,W为该类节点的个数;ω(Si, jd(θ, t), Sw, jd(θ, t))为直接评估结果的相似性,若低于阈值,则忽略,并以基本速率记录该节点恶意行为.相似性采用复杂度较低的Tanimoto方法计算:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \omega (\mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t),\mathit{\boldsymbol{S}}_{w,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t)) = \\ A\frac{{\mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t),\mathit{\boldsymbol{S}}_{w,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t)}}{{\mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t),\mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t) + \mathit{\boldsymbol{S}}_{w,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t)\mathit{\boldsymbol{S}}_{w,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t) - \mathit{\boldsymbol{S}}_{i,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t),\mathit{\boldsymbol{S}}_{w,j}^{\rm{d}}(\mathit{\boldsymbol{\theta }},t)}} \end{array} $ | (10) |
其中A为评价结果相似性的最高采纳权重.
| $ \gamma (i,w) = \left\{ {\begin{array}{*{20}{l}} {\frac{2}{3}, {\rm{rel}} (i,w) = {\rm{ Friends }}}\\ {\frac{1}{3}, {\rm{rel}} (i,w) = {\rm{ Strangers }}} \end{array}} \right. $ | (11) |
式(11)表示对于不同社交关系的节点w,节点i将采取不同信任权重.
选取最高概率的可信程度,节点i得到对于节点j的最终评估结果为
| $ {E_{i,j}} = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{max}}}\limits_{{\theta _k}} {\mathit{\boldsymbol{S}}_{i,j}}(\mathit{\boldsymbol{\theta }},t) $ | (12) |
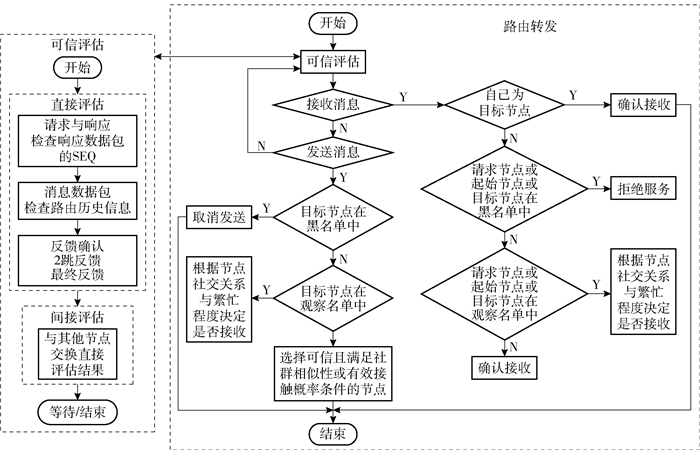
如图 2所示,算法流程包括节点的可信评估和路由转发策略2部分.
|
图 2 算法流程示意图 |
1) 请求与响应
请求方检查响应数据包的响应标记位(ACK,acknowledge),如果为1,表示同意接收.继续检查序号标记位(SEQ,sequence),若该值与之前发送值相差1,表示响应方表现正常,以基本速率记录正常行为;如果SEQ没有变化,以二倍速记录恶意行为.若ACK位为0,表示响应方拒绝服务,以二倍速记录自私行为.超过请求数据包生存时间后,仍未收到响应数据包,以基本速率记录响应方自私行为.如果请求节点在观察名单中,但不是起始节点,则认定其为社交型自私节点,令其flag=1.
2) 消息数据包
从消息数据包中获取路由记录,奖励所有参与中继的节点,以半速记录正常行为.若出现观察名单中的节点,则判定其为社交型自私节点,令其flag=1.
3) 反馈确认
根据反馈信息的节点是否为目标节点,将反馈确认过程分为以下2种情况.
① 2跳反馈.非目标节点将接收的消息的哈希值MSGID发送给2跳前的节点.
如果MSGID存储于接收反馈消息的节点中,则对反馈信息中包含的中继节点以二倍速记录正常行为.
对于反馈信息的来源,如果来自黑名单中的节点,说明该节点在接收到消息数据包后并未直接丢弃,以基本速率记录正常行为;如果来自观察名单中的节点,说明其为社交型自私节点,令其flag=1.
如果不存在对应MSGID,则直接丢弃该反馈数据包.
② 最终反馈.目标节点将反馈发送给路径中出现的所有节点.
确认MSGID存在本地后,对路径中的其他节点以二倍速记录一次正常行为;否则,忽略该反馈信息.
直接评估结果如式(8)所示.
2.1.2 间接评估流程节点间定期交换自身的直接评估结果,作为建议信息.间接评估结果如式(9)所示.
间接评估对于直接评估的补充:当由式(10)计算的相似性不满足阈值时,以基本速率记录来源节点的恶意行为;当接收到观察名单中节点的评估结果时,表明该节点参与到了网络通信过程中,以二倍速记录正常行为.
根据式(1)和式(12),获得节点的可信程度.
2.2 路由转发流程路由转发包括面对请求时如何响应以及发送消息时如何选择中继2种情况.设定可信程度较高节点的消息数据具有更高的处理优先级.
情况1 面对中继请求的响应
第1步 如果自己为目标节点,一律接收;否则,跳转到第2步.
第2步 如果请求节点、起始节点或目标节点为恶意节点(在黑名单中),则直接反馈表示该次请求不合格,并拒绝服务;否则,跳转到第3步.
第3步 如果请求节点、起始节点或目标节点为自私节点(在观察名单中),若flag=1,则跳转到第4步.根据资源空闲情况与设定阈值(朋友关系时,采取较低阈值)的比较结果,利用响应数据包回复同意或拒绝服务;否则,跳转到第4步.
第4步 确认接收.
情况2 选择中继节点向目标节点发送数据包
第1步 如果目标节点为恶意节点(在黑名单中),则取消发送计划;否则,跳转到第2步.
第2步 如果目标节点为自私节点(在观察名单中),若flag=1,则跳转到第3步.根据资源空闲情况与设定阈值(朋友关系时,采取较低阈值)的比较结果来判定是否执行发送计划;否则,跳转到第3步.
第3步 在经过狄利克雷评估获得的可信节点基础上,选择满足社群相似性或有效接触概率的节点作为中继节点.
① 社群相似性.描述中继节点与目标节点同属一个社群的可能性.令tar代表目标节点,c代表候选节点,则社群相似性表示为
| $ {\rm{Sim }}({\mathit{\boldsymbol{R}}_c},{\mathit{\boldsymbol{F}}_{{\rm{tar}}}}) = 1 - \sqrt {\frac{{\sum\limits_{n = 1}^N {(\mathit{\boldsymbol{R}}_c^n(} f_{{\rm{tar}}}^n) - 1{)^2}}}{N}} $ | (13) |
其中:Rc以表格的形式将候选节点c存储在本地社群中的所有属性及其记录值中,Ftar为目标节点tar的社会属性.
② 有效接触概率.描述两节点间传递数据包的历史概率,近似为指数分布,通过分析路由信息可得到.发生直接传递的事件次数为1,而间接传递的事件次数随路由距离的增大而衰减.当前时间窗τ内发生有效接触事件X的概率为
| $ {q_{c,{\rm{ tar }}}}(X \le \tau ) = 1 - {q_{c, {\rm{tar}} }}(X > \tau ) = 1 - {{\rm{e}}^{ - {\lambda _{c, {\rm{tar}} }}(t)\tau }} $ | (14) |
其中λc, tar(t)为当前单位时间内有效接触事件X的平均次数,则
| $ {\lambda _{c,{\rm{ tar }}}}(t + \tau ) = \beta {\lambda _{c,{\rm{ tar }}}}(t) + (1 - \beta )\sum\limits_{r = 1}^{P(t,t + \tau )} {{{\rm{e}}^{ - \mu ({d_r}(c,{\rm{ tar }} ) - 1)}}} $ | (15) |
其中:μ为受路由距离影响的衰减因子,dr(c, tar)为节点c与tar之间的路由距离,P(t, t+τ)为新时间窗内接收的消息数据包数,
在可信的基础上,节点选择需要进一步满足下列条件:
| $ \begin{array}{l} {\rm{Sim }}({\mathit{\boldsymbol{R}}_c},{\mathit{\boldsymbol{F}}_{{\rm{ tar }}}}) > {\rm{Sim }} ({\mathit{\boldsymbol{R}}_{{\rm{ cur }}}},{\mathit{\boldsymbol{F}}_{{\rm{ tar }}}}) \cup {q_{c, {\rm{tar}} }}(X \le \tau ) > \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_{{\rm{ cur , tar }}}}(X \le \tau ) \end{array} $ | (16) |
其中cur代表当前节点.式(16)表示候选节点需要满足社交相似性大于当前节点或者有效接触概率大于当前节点.
3 仿真实现 3.1 仿真环境仿真环境选择机会网络环境仿真器,从Infocom06的真实数据筛选出78位用户4 d的接触信息,采用国籍、国家、城市、语言、公司和职位信息描述节点.参数如下:20次,300 000 s,传输速率为54 Mbit/s,传输范围为30 m,存储空间为100 MB,数据生存时间为12 h,用户为78个,不良节点变化比例为0~80%.
3.2 结果分析将所提出的TRFDD与Epidemic[8]、Prophet[9]、TRSS[4]进行对比,并采用传输成功率、传输成本、传输时延和丢包数量4个评价指标.
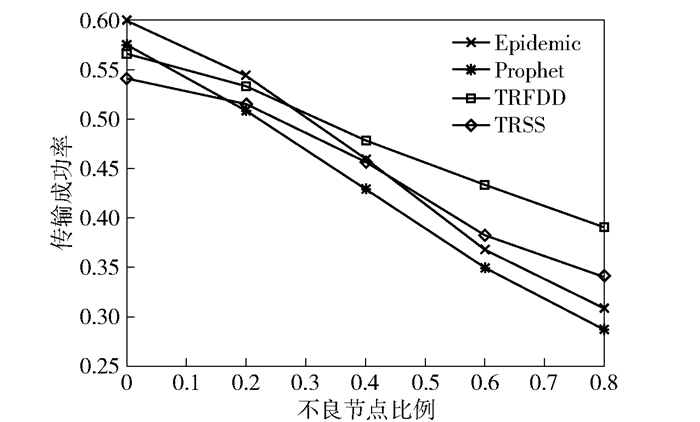
3.2.1 传输成功率传输成功率是指成功传输的次数与所有发送事件数的比值.如图 3所示,所有算法的传输成功率均随着不良节点的增多而下降,但TRFDD始终保持较高的成功率,很快超过Epidemic和Prophet.当不良节点比例达到80%时,TRFDD的传输成功率比TRSS高出5%,比Epidemic高出9%,比Prophet高出11%.
|
图 3 传输成功率对比 |
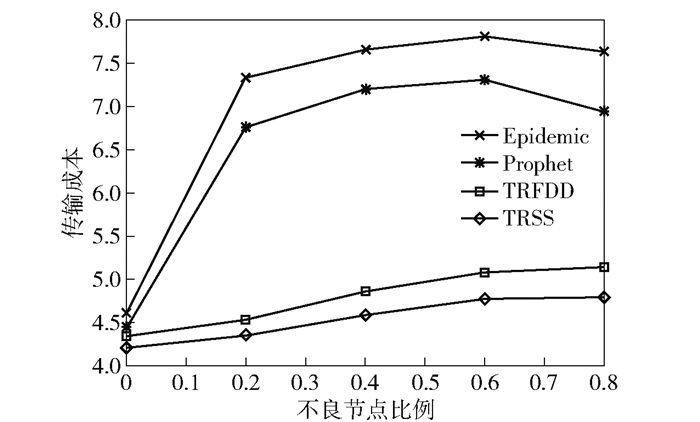
传输成本是指为实现单个消息数据包成功接收所需复制转发的次数,采用对数表示.如图 4所示,Epidemic和Prophet的传输成本急速升高,随后保持稳定;TRFDD和TRSS的传输成本始终处于较低的水平. TRFDD的传输成本虽然略高于TRSS,但传输成功率高出5%,效率较高.
|
图 4 传输成本对比 |
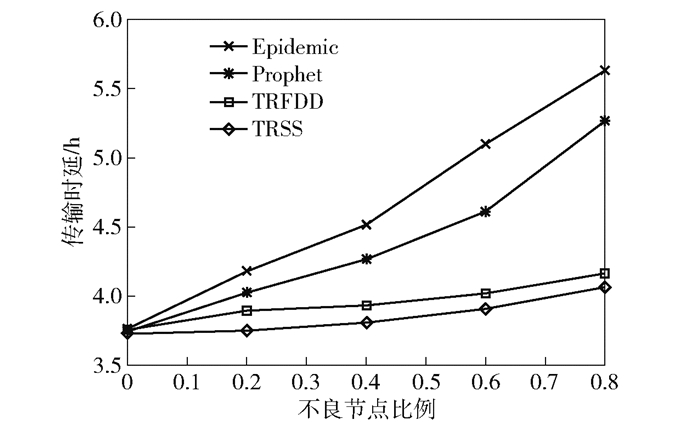
传输时延是指消息数据包成功接收与生成时刻的时间差.如图 5所示,Epidemic和Prophet算法的传输时延增长速率逐渐加快,在80%不良节点比例下达到5.5 h,接近数据生存时间;而TRFDD和TRSS的传输时延相近始终保持在4 h内.
|
图 5 传输时延对比 |
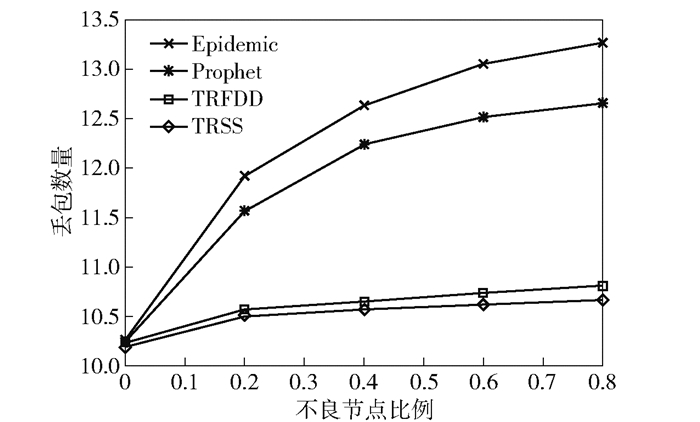
丢包数量描述在传输过程中因生存时间超时、不良节点丢弃等原因所造成的数据包丢失,用以衡量网络资源的浪费情况,采用对数表示.如图 6所示,Epidemic和Prophet的丢包数量提高了2~3个数量级,而TRFDD和TRSS的丢包数量相近,且仅在小范围内增长.
|
图 6 丢包数量对比 |
为解决机会移动社群网络中由于节点的不良行为所导致的内容资源共享效率和质量下降的问题,提出了TRFDD以维护网络的正常通信过程.首先利用消息传递过程中获取的信息从多个维度判断节点的可信程度,进而提出了正常节点对不良节点的应对算法,采取了尽量与自私节点合作,拒绝与恶意节点合作的策略.与目前主流的相关算法进行对比实验,结果显示所提出的算法能够有效地避免不良节点的干扰,具有较强的鲁棒性.通过准确评估节点的可信程度、充分挖掘社交型自私节点能力等方式,高效地维持了较高的传输成功率,实现了数据包的快速转发,有效地避免了不良行为所引起的网络失衡现象.
| [1] |
程伟明. 无线移动自组网及其关键技术[J]. 数据通信, 2002(3): 56-58. Cheng Weiming. Wireless mobile Ad hoc network and its key technologies[J]. Data Communication, 2002(3): 56-58. DOI:10.3969/j.issn.1002-5057.2002.03.016 |
| [2] |
Mukherjee P, Sen S. Comparing reputation schemes for detecting malicious nodes in sensor networks[J]. The Computer Journal, 2011, 54(3): 482-489. DOI:10.1093/comjnl/bxq035 |
| [3] |
Chen Xi, Sun Liang, Ma Jianfeng, et al. A trust management scheme based on behavior feedback for opportunistic networks[J]. Network Technology and Application, 2015, 12(4): 117-129. |
| [4] |
Yao Lin, Man Yanmao, Huang Zhong, et al. Secure routing based on social similarity in opportunistic networks[J]. IEEE Transactions on Wireless Communications, 2015, 15(1): 594-605. |
| [5] |
Josang A, Haller J. Dirichlet reputation systems[C]//International Conference on Availability, Reliability and Security. Vienna: IEEE Press, 2007: 112-119.
|
| [6] |
Li Yang, Kizza J M, Alma-Cemerlic, et al. Fine-grained reputation-based routing in wireless Ad hoc networks[C]//Intelligence and Security Informatics. New Brunswick: IEEE Press, 2007: 75-78.
|
| [7] |
Denko M K, Sun Tao, Woungang I. Trust management in ubiquitous computing:a Bayesian approach[J]. Computer Communications, 2011, 34(3): 398-406. DOI:10.1016/j.comcom.2010.01.023 |
| [8] |
Vahdat A, Becker D. Epidemic routing for partially-connected Ad hoc networks[J]. Master Thesis, 2000, 20(4): 106-119. DOI:10.1145/1341771.1341791 |
| [9] |
Zhou Hongbo, Ni L M, Mutka M W. Prophet address allocation for large scale MANETs[J]. Ad Hoc Networks, 2003, 1(4): 423-434. |


