针对合法接收端采用全双工模式时的自干扰消除问题,提出了一种在单输入多输出系统中,利用神经网络实现全双工合法接收端信号合并和自干扰消除的方案.合法接收端在接收信号的同时发送人工噪声干扰窃听者.设计2个神经网络,一个用于接收信号的合并,另一个对接收信号中的自干扰进行对消.对合法接收端和窃听端的误比特率、可达保密速率等性能进行仿真的结果表明,信号合并和自干扰消除方案可行并有效,在适当配置接收端发射天线和接收天线数量后,可获得可观的系统保密速率.
Aiming at the problem of self-interference cancellation when the full-duplex mode is adopted by the legitimate receiver, a scheme is presented for signal combining and self-interference cancellation based on neural networks at the full-duplex legitimate receiver in a single-input multi-output system. The legitimate receiver, while receiving signals, sends artificial noise to interfere with the eavesdropper. Two neural networks are designed, one combining the signals received by multiple antennas, and the other reconstructing self-interference for the self-interference cancellation of the received signals. The bit error rates of the legitimate receiver and the eavesdropper and the achievable secrecy rate are simulated. The simulation results show that the signal combination and self-interference cancellation scheme is feasible and effective. They also show that a considerable secrecy rate can be achieved when the transmitting antennas and receiving antennas at the legitimate receiver are properly allocated.
物理层安全是一种基于信息论的安全方法,通过使用信道编码和信号处理技术实现信息的保密传输.无线通信系统中,提高物理层安全保密传输速率的一种有效方法是引入受控干扰来降低窃听者接收信号的质量[1].受控干扰可由信息发送端、协同干扰者发送,也可由工作在全双工(FD, full duplex)模式的接收端在接收信息的同时发送. Li等[2]首次提出利用FD接收机发送干扰来提高保密性能. Zheng等[3]利用FD接收机作为友好干扰者,优化物理层安全方案的性能. Masood等[4]针对包含多天线窃听端和多天线FD接收机的系统模型,对发射机保密信号与人工噪声的协方差、合法接收机发送的人工噪声的协方差进行联合优化,以实现保密速率的最大化. Li等[5]和Guo等[6]分别对FD接收机自干扰可完全消除和不能完全消除2种情况下的物理层安全方案进行了研究.这些研究的结果都表明,通过FD模式的接收端进行协同干扰,可有效提高系统的物理层安全性能.但在这些研究中均假设系统自干扰可完全或部分消除(利用残余自干扰模型),没有给出具体的自干扰消除方案.
神经网络具有学习与适应不确定系统动态特性的特点,在信号和信息处理中已有很多应用. Anitha等[7]和Sallomi等[8]将神经网络应用于智能天线的自适应波束赋形中,使用神经网络来计算天线阵列的最佳权重.桂冠等[9]对深度神经网络在无线通信物理层上可能的应用,包括波束赋形、调制模式识别等进行了讨论. Song等[10]研究协作节点发送人工噪声的物理层安全传输系统,提出采用误差反向传播(BP)神经网络实现对信道的高精度估计,有效提高了系统保密速率.
与现有文献在FD接收端的自干扰可完全消除或存在残余的假设下,进行物理层安全方案的设计和优化工作不同,笔者研究了物理层安全系统中FD自干扰的消除和接收信号的合并问题.在单输入多输出(SIMO, single input multi output)窃听信道模型下,利用神经网络实现接收端的信号合并和自干扰消除.系统中的合法接收机工作在FD模式,在接收信息的同时,发送人工噪声干扰窃听者的接收.多接收天线接收到的信号先经过一个神经网络进行合并,然后再由干扰重构器消除接收信号中的自干扰.自干扰消除过程包括2步:先用神经网络根据发送的人工噪声构造与接收信号中的自干扰信号类似的对消信号,然后将其与接收信号进行减法运算消除其中的自干扰.通过仿真对合并器与自干扰重构器的有效性进行了验证,并对Eve端已知信道状态信息(CSI, channel state information)和CSI事先未知两种情况下的保密速率进行了仿真和分析.
1 系统模型考虑包括一个发送者Alice、一个合法接收者Bob和一个被动窃听者Eve组成的系统模型,如图 1所示. Alice、Bob、Eve配备的天线数分别为1、NB、NE. Bob采用天线分离式FD模式,Nr根天线用于接收,其他Nt根天线用于发送,Nr+Nt=NB. Alice和Bob未知窃听信道的任何信息,因此采用Bob在接收Alice所发信号的同时发送全向人工干扰的方式增强安全性能.分别用hBA∈ℂNr×1、hEA∈ℂNE×1、HEB∈ℂNE×Nt表示Alice与Bob间、Alice与Eve间、Bob与Eve间的信道增益. Bob的收发天线之间存在自干扰,包含路径损耗和模拟对消干扰抑制环节的自干扰信道增益,表示为HBB∈ℂNr×Nt.
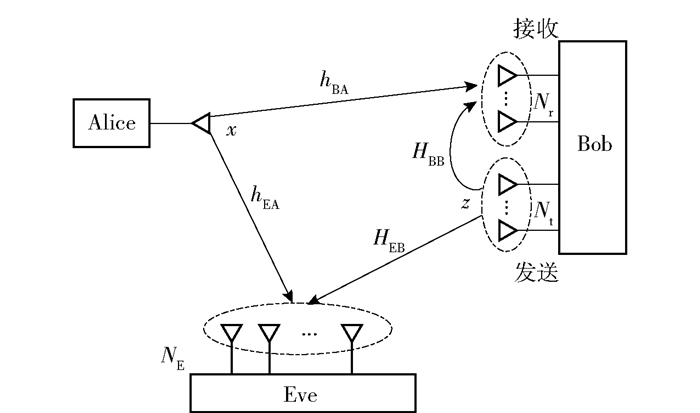
|
图 1 接收端全双工系统模型 |
对于Bob端,其接收信号可表示为
| $ {\mathit{\boldsymbol{r}}_{\rm{B}}} = \sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{BA}}}}x + \sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{BB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{B}}} $ | (1) |
其中:x表示Alice发送的符号;z表示Bob随机生成的Nt维人工噪声矢量,均为单位功率;Px为Alice发送保密信号的功率;Pz为Bob发送人工噪声的功率;nB为Bob接收到的Nr维复加性高斯白噪声矢量,矢量元素的方差为σB2.
为使Bob能够正常检测接收信号,需对接收信号中的自干扰进行对消,并对多根接收天线的接收信号进行合并.笔者讨论数字域的自干扰消除问题,假设已通过天线自干扰消除和模拟自干扰消除实现了部分自干扰抑制,抑制度已包含在自干扰信道增益HBB中. Bob的信号处理模型如图 2所示.信号合并利用线性神经网络实现,合并信号为

|
图 2 接收机模型框图 |
| $ r_{\rm{B}}^{{\rm{com}}} = {f_w}({\mathit{\boldsymbol{r}}_{\rm{B}}}) = {f_w}(\sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{BA}}}}x + \sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{BB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{B}}}) $ | (2) |
其中fw(·)表示信号合并器的合并作用函数(线性函数).自干扰消除后的信号可表示为
| $ \begin{array}{*{20}{c}} {{y_{\rm{B}}} = r_{\rm{B}}^{com} - {{\tilde r}_z} = }\\ {{f_w}(\sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{BA}}}}x + \sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{BB}}}}\mathit{\boldsymbol{z}} + {n_{\rm{B}}}) - {f_z}(\mathit{\boldsymbol{z}}) = }\\ {{f_w}(\sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{BA}}}}x) + ({f_w}(\sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{BB}}}}\mathit{\boldsymbol{z}}) - {f_z}(\mathit{\boldsymbol{z}})) + {f_w}({\mathit{\boldsymbol{n}}_{\rm{B}}})} \end{array} $ | (3) |
其中:
线性神经网络[11]是一种简单的神经元网络,主要用于解决线性问题,其结构如图 3所示.由于本文信道模型为平坦衰落信道模型,所以这里采用了单层神经网络,如果信道为频率选择性衰落信道,存在可分辨的多径,则需要采用多层神经网络.

|
图 3 线性神经网络 |
信号合并器使用图 3所示的线性神经网络,输入层节点数为Nr.训练时,Alice端发射伪随机训练序列xp,Bob端不发送人工噪声. Bob端接收到的信号为
| $ {\mathit{\boldsymbol{y}}_{\rm{p}}} = {\mathit{\boldsymbol{h}}_{{\rm{BA}}}}{x_{\rm{p}}} + {\mathit{\boldsymbol{n}}_{\rm{B}}} $ | (4) |
合并器的期望输出为xp,神经网络训练的目标是使合并器的输出与xp的均方误差最小.信道的输出yp为神经网络的输入,因此训练样本对为(yp, xp).神经网络的输入为Bob接收天线接收到的信号,输出就是合并后的信号.
自干扰重构器的训练在信号合并神经网络训练完成后进行.自干扰重构器同样使用图 3所示的线性神经网络,输入层节点数为Nt.自干扰重构神经网络训练时,Alice不发送信号,Bob的发射天线发送随机人工噪声z作为训练序列,Bob接收天线接收的信号为
| $ {\mathit{\boldsymbol{r}}_{{\rm{AN}}}} = {\mathit{\boldsymbol{H}}_{{\rm{BB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{B}}} $ | (5) |
该信号进入自干扰重构器前先进行信号合并:
| $ r_{{\rm{AN}}}^{{\rm{com}}} = {f_w}({\mathit{\boldsymbol{r}}_{{\rm{AN}}}}) = {f_w}({\mathit{\boldsymbol{H}}_{{\rm{BB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{B}}}) $ | (6) |
自干扰重构器的输入信号为z,期望输出为经过合并后的、经过天线和模拟自干扰消除后残余的人工噪声rANcom.自干扰重构器训练的目标是使其输出与rANcom的均方误差最小,这样经过自干扰对消后就能最大限度地消除接收信号中的自干扰.因此,自干扰重构器训练时的训练样本对为(z, rANcom).
在两个神经网络训练完成后,就可以开始正常的信息传输过程.训练过程中不能传输信息,会带来一定的开销,训练序列的长度越短,信道变化越慢,则开销就越小.后面的仿真中可以看到,在训练序列长度为50时就能获得很好的训练效果,对于常规运动速度下的移动通信系统,信道变化周期为毫秒级,这样的训练开销是可以接受的.实际上,任何采用非盲信道估计的系统中都存在训练开销.
3 保密速率分析 3.1 可达保密速率合法信道容量为
| $ \begin{array}{*{20}{c}} {{C_{\rm{B}}} = {\rm{lb}}(1 + {\gamma _{\rm{B}}}) = }\\ {{\rm{lb}}\left( {1 + \frac{{{P_x}|{f_w}({\mathit{\boldsymbol{h}}_{{\rm{BA}}}}x){|^2}}}{{|\sqrt {{P_z}} {f_w}({\mathit{\boldsymbol{H}}_{{\rm{BB}}}}\mathit{\boldsymbol{z}}) - {f_z}(\mathit{\boldsymbol{z}}){|^2} + |{f_w}({\mathit{\boldsymbol{n}}_{\rm{B}}}){|^2}}}} \right)} \end{array} $ | (7) |
其中:γB为Bob的接收信干噪比. Eve的接收信号为
| $ {\mathit{\boldsymbol{r}}_{\rm{E}}} = \sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{EA}}}}x + \sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{EB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{E}}} $ | (8) |
其中:nE为Eve接收到的NE维复加性高斯白噪声矢量,矢量元素的方差为σE2.
Eve可采用某种方案对各天线上接收的信号进行合并处理后进行检测,处理后的信号表示为
| $ {y_{\rm{E}}} = {\mathit{\boldsymbol{w}}_{\rm{E}}}{\mathit{\boldsymbol{r}}_{\rm{E}}} = {\mathit{\boldsymbol{w}}_{\rm{E}}}(\sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{EA}}}}x + \sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{EB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{E}}}) $ | (9) |
其中:wE∈ℂ1×NE为Eve的接收处理矢量.窃听信道容量为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{\rm{E}}} = {\rm{lb}}(1 + {\gamma _{\rm{E}}}) = \\ {\rm{lb}}\left( {1 + \frac{{{P_x}|{\mathit{\boldsymbol{w}}_{\rm{E}}}{\mathit{\boldsymbol{h}}_{{\rm{EA}}}}{|^2}}}{{{P_z}{{\left\| {{\mathit{\boldsymbol{w}}_{\rm{E}}}{\mathit{\boldsymbol{H}}_{{\rm{EB}}}}} \right\|}^2} + {{\left\| {{\mathit{\boldsymbol{w}}_{\rm{E}}}} \right\|}^2}\sigma _{\rm{E}}^2}}} \right) \end{array} $ | (10) |
其中:‖·‖表示向量的2-范数,γE为Eve的接收信干噪比.可达保密速率为
| $ {R_{\rm{S}}} = {\rm{max}}\{ 0,{C_{\rm{B}}} - {C_{\rm{E}}}\} $ | (11) |
本节分别在Eve端能准确获得CSI和事先未知CSI 2种情况下仿真和分析方案的保密性能. 2种CSI条件下,Eve采取不同的信号处理方案. Eve能准确获得CSI时其可获得最好的接收性能,是对安全通信最不利的场景.但实际上Eve要获得准确的CSI是非常困难的.
3.2.1 CSI已知在已知CSI,即hEA与HEB时,Eve可采用最大比合并(MRC, maximum ratio combining)、迫零(ZF, zero forcing)和最小均方误差(MMSE, minimum mean squared error)等合并处理方案.这3种方案的接收处理矢量分别为
| $ {{\mathit{\boldsymbol{w}}_{\rm{E}}} = {\mathit{\boldsymbol{w}}_{{\rm{MRC}}}} = \mathit{\boldsymbol{h}}_{{\rm{EA}}}^{\rm{H}}} $ | (12) |
| $ {{\mathit{\boldsymbol{w}}_{\rm{E}}} = {\mathit{\boldsymbol{w}}_{{\rm{ZF}}}} = {{(\mathit{\boldsymbol{H}}_{{\rm{EB}}}^{\rm{H}}{\mathit{\boldsymbol{H}}_{{\rm{EB}}}})}^{ - 1}}\mathit{\boldsymbol{h}}_{{\rm{EA}}}^{\rm{H}}} $ | (13) |
| $ {{\mathit{\boldsymbol{w}}_{\rm{E}}} = {\mathit{\boldsymbol{w}}_{{\rm{MMSE}}}} = {{\left( {\mathit{\boldsymbol{H}}_{{\rm{EB}}}^{\rm{H}}{\mathit{\boldsymbol{H}}_{{\rm{EB}}}} + \frac{{\sigma _{\rm{E}}^2}}{{{P_z}}}{\mathit{\boldsymbol{I}}_{{N_{\rm{E}}}}}} \right)}^{ - 1}}\mathit{\boldsymbol{h}}_{{\rm{EA}}}^{\rm{H}}} $ | (14) |
其中:上标H表示矢量或矩阵的共轭转置.
3.2.2 CSI未知Eve在未知信道CSI时,可在合法通信的双方进行合并器和自干扰重构器训练时,根据Alice和Bob发送的训练信号得到信号的接收处理矢量.进行信号合并器训练时,Alice端发送伪随机的训练序列xp,假设Eve已知该训练序列,可利用接收到的训练序列采用某种准则,如MMSE准则对hEA进行估计.假设估计值为
进行自干扰重构器进行训练时,Bob发送随机的人工噪声z作为训练序列,因此Eve不可能事先已知,但其可根据接收信号进行针对性的干扰抑制处理.下面给出一种方案,用于评估Eve未知CSI下的安全性能. Bob训练自干扰重构器时,Eve的收到信号为rEAN=HEBz+nE,对rEAN的自相关矩阵
| $ {\mathit{\boldsymbol{y}}_{\rm{E}}} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{r}}_{\rm{E}}} = \mathit{\boldsymbol{F}}(\sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{EA}}}}x + \sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{EB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{E}}}) $ | (15) |
然后利用估计得到的
| $ {y_{\rm{E}}} = \mathit{\boldsymbol{\tilde h}}_{{\rm{EA}}}^{\rm{H}}{y_{\rm{E}}} = \mathit{\boldsymbol{\tilde h}}_{{\rm{EA}}}^{\rm{H}}\mathit{\boldsymbol{F}}(\sqrt {{P_x}} {\mathit{\boldsymbol{h}}_{{\rm{EA}}}}x + \sqrt {{P_z}} {\mathit{\boldsymbol{H}}_{{\rm{EB}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{E}}}) $ | (16) |
将干扰抑制和信号合并用一个矢量乘法运算来描述:
| $ {y_{\rm{E}}} = {\mathit{\boldsymbol{w}}_{\rm{E}}}{\mathit{\boldsymbol{r}}_{\rm{E}}} $ | (17) |
其中接收处理矢量
本节仿真中,所有信道均是瑞利平坦衰落信道;Bob和Eve的天线数分别为6和4;Alice天线与Bob、Eve各接收天线间的信道增益均为独立同分布的复高斯随机变量,均值为0,方差为1010;假设Bob的自干扰信道的路径损耗为40 dB,根据相关文献中的报道,现有的模拟自干扰重构器的抑制度可到达40 dB,因此仿真中HBB中各元素为均值为0,方差为108的复高斯随机变量;各天线处的信道噪声方差为σB2=σE2=-100 dBm;Alice发送保密信号的功率与Bob发送人工噪声的功率相等,即Px=Pz=P;所有神经网络的训练序列长度均为50,训练序列的发射功率与数据传输过程中保密信号或人工噪声的功率相同.误比特率(BER, error bit rate)仿真中,调制方式为QPSK,每个参数下要在Bob的错误比特数达到1 000时才停止仿真.保密速率与信道容量的仿真结果为信道随机变化10 000次的蒙特卡罗仿真结果的平均值.所有接收方案的误比特率仿真中,Bob和Eve的信号检测方式都是最大似然检测.
图 4为Bob不同的发射和接收天线数量组合时,其误比特率BER随发送功率P变化的仿真结果.同时给出Bob自干扰信号可完全消除、信号合并采用准确CSI下的MRC方式时的性能作为对比,此方案具有最好的性能,图中标识为“理想方案”.从图 4中可以看出,Nr越大,BER越低.这是因为接收天线越多,Bob接收信号平均功率和分集增益越大.本文方案与理想方案的BER非常接近,表明笔者所设计的自干扰消除器干扰消除效果较好,信号合并器的性能很接近MRC合并器的性能.
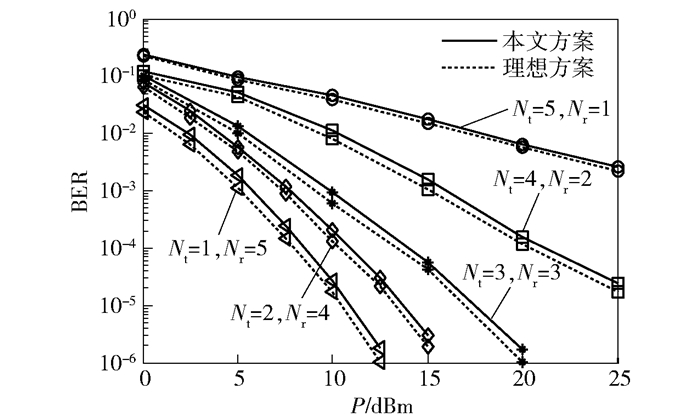
|
图 4 Bob端不同天线配置时的误比特率 |
图 5为在Eve已知CSI的情况下,使用不同的接收方式时其BER随P变化的仿真结果.仿真中,Nt=4,Nr=2. Eve端分别采用MRC、ZF和MMSE接收方式.从图 5可以看出,Eve使用ZF和MMSE方式的BER明显低于MRC方式,这是因为ZF和MMSE方式都考虑了对Bob所发人工噪声的抑制,而MRC仅根据hEA进行信号合并. P较低时,相比较ZF方式,MMSE方式的BER更低,而在P足够大后,ZF与MMSE方式的性能基本一致.这是因为进行干扰抑制时,MMSE方式考虑了信道噪声的影响,而ZF方式没有. 图 6为对应Eve三种接收方式时系统可达保密速率的仿真结果.与误比特率的仿真结果相对应,Eve采用MRC方式时保密速率最高,采用ZF与MMSE方式时的保密速率较低,且在P较低时,MMSE方式的保密速率要低于ZF方式.可见,Eve采用MMSE方式时具有相对较好的性能,是对保密传输最不利的情况,因此在本节随后Eve已知CSI时的仿真中,只给出其采用MMSE方式时的仿真结果.

|
图 5 Eve端使用不同接收处理方式时的误比特率 |
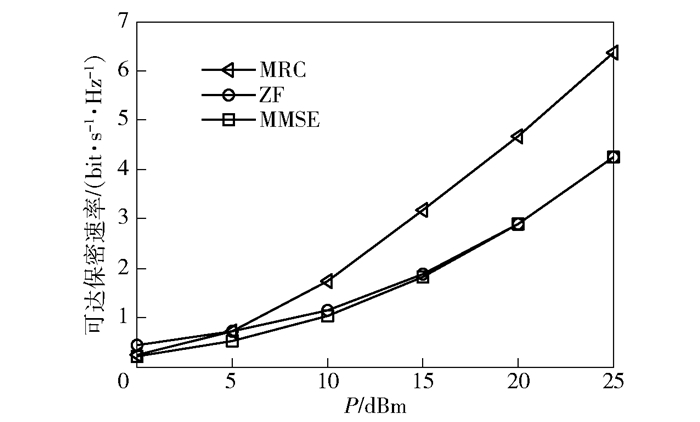
|
图 6 Eve端使用不同接收处理方式时的保密速率 |
图 7为Bob采用不同的发射和接收天线数量组合时,Eve在CSI已知和未知2种情况下BER随P变化的仿真结果.从图 7中可以看出,Eve已知CSI时的BER始终要比CSI未知时低. Eve已知CSI时,可更好地对Bob发送的人工噪声进行抑制,对各天线接收信号的合并效果也更好.而在CSI未知时,虽可对hEA进行估计,但由于估计存在误差,影响合并效果;而对于Bob发送的人工噪声,只能根据Bob训练自干扰重构器时发送的随机噪声得到干扰抑制矩阵,抑制效果必然不如CSI已知时.随着Bob发送天线数Nt增大,Eve的BER也增大. Nt越大,即干扰源越多,Eve更难抑制干扰.当Nt≤3时,Eve的BER随着P的增大持续下降;而当Nt=4、5时,BER并不能随着P的增大而下降.这是因为仿真中固定窃听天线数NE=4,当NE>Nt时,Eve能利用空间自由度对干扰进行有效的抑制,接收性能较好;而当NE≤Nt时,Eve不能很好地抑制干扰,其接收信号中的干扰功率与信号功率是同步变化,Eve接收信号的信干噪比并不能随P增加而相应改善,因此BER不能随P增加而持续下降.该仿真结果表明,从抑制窃听者窃听的角度看,Bob的发送天线不应少于Eve的天线.
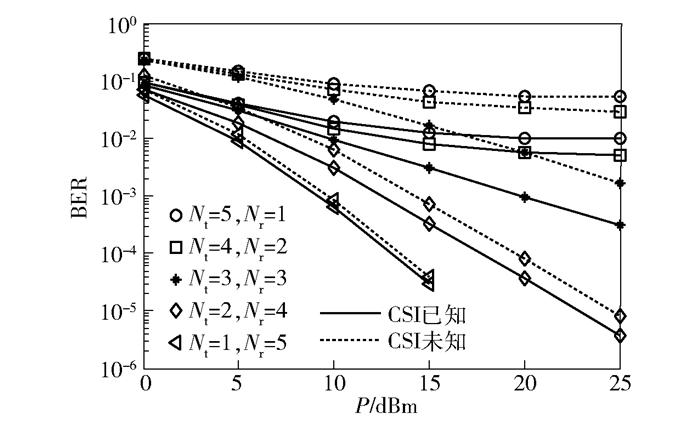
|
图 7 Bob端不同天线配置时Eve端的误比特率 |
图 8为Bob采用不同的发射和接收天线数量组合时,合法信道和窃听信道容量、系统可达保密速率随P变化的仿真结果.对于Bob,Nr越大,接收性能越好,因此信道容量越大,如图 8(a)所示.对于Eve,如图 8(b)所示,当Nt≤3时,其能较好地抑制干扰,信干噪比随P增加而增加,因此窃听信道容量随P的增大而持续增大;而当Nt=4、5时,干扰源数量已大于Eve的接收天线数,其不能很好地抑制干扰信干噪比不能随P增加而增加,相应窃听信道容量不能随P增大而增大.这与图 7误码性能的仿真结果是吻合的.保密速率的仿真结果如图 8(c)所示. Bob发送天线数较少时(Nt≤3),窃听信道容量能随P的增加而持续增加,增加速度与合法信道容量基本相当,因此可达保密速率仅在P较低时能随P的增加有少量增加,但当P增加到一定程度后就基本不再增加.而在Bob发送天线数较多时(Nt≥4),虽然合法信道容量较发送天线较少时低,但由于此时Eve不能有效地抑制人工噪声,窃听信道容量不能随P增加而持续增加,因此保密速率可随P的增加而增加.可以发现Bob配置4根发送天线时安全性能最优,这是因为Eve配备了4根天线,当Bob用4根天线发送人工噪声时,Eve就已不能有效抑制干扰.再增加发送天线,虽然对Eve的干扰有所增强,但由于接收天线减少,Bob的接收性能有较大的下降,反而导致保密速率下降.因此,分配Eve天线数相同数量的天线发送干扰,其他天线进行信号接收时具有最好的安全性能.
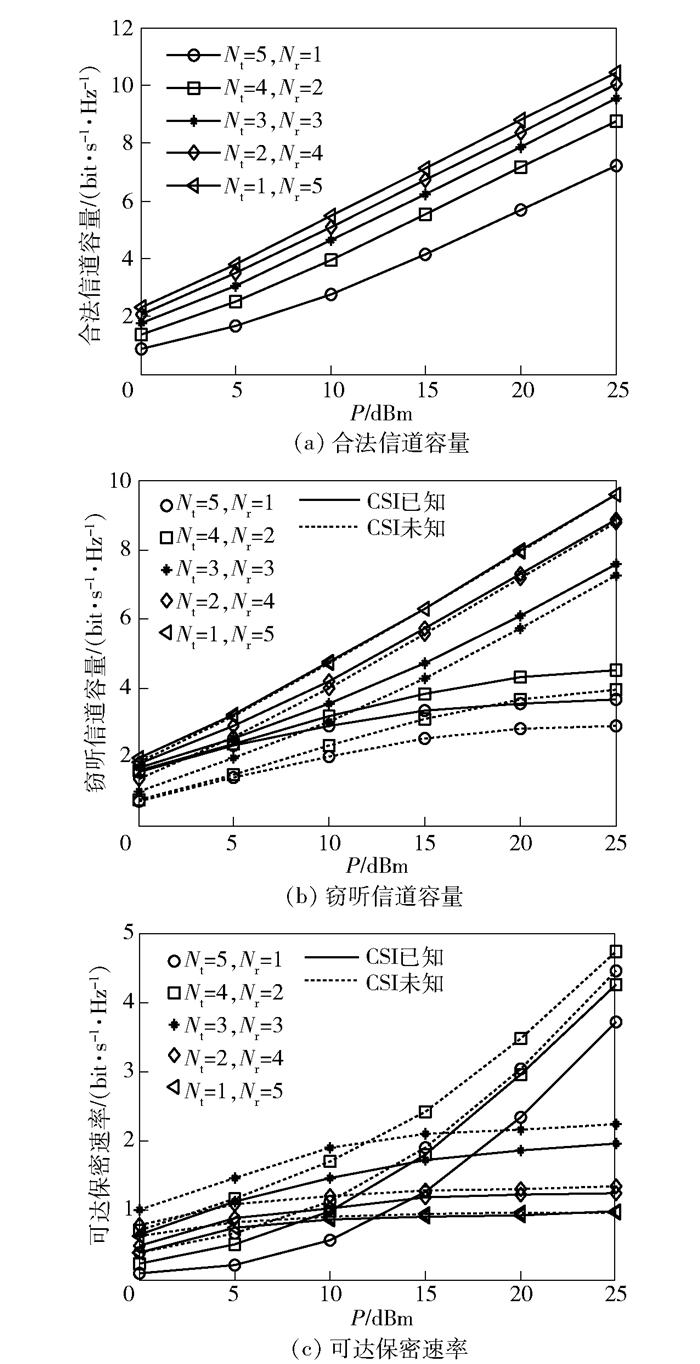
|
图 8 Bob端不同天线配置时的系统性能 |
针对合法接收端采用FD模式,在接收信号的同时发送人工噪声的物理层安全传输系统,提出了接收端采用线性神经网络的信号合并和自干扰消除方案.方案中采用2个神经网络,其中一个对多接收天线接收的信号进行合并,另一个根据发送的人工噪声构造与接收自干扰相似的信号,用于对消接收信号中收发通道间的自干扰.对合法接收端和窃听端的误比特率、合法信道和窃听信道容量、可达保密速率等性能进行了仿真.仿真结果显示,采用本文方案时Bob的接收误码性能与自干扰完全消除,且采用MRC合并的理想方案的误码性能非常接近,合法信道容量随发送功率增加可持续增加,证明本文所提的信号合并和自干扰消除方案是可行和有效的.在Eve准确已知CSI和CSI事先未知两种情况下,对Eve采用不同接收处理方式时的误码性能、窃听信道容量和系统可达保密传输速率进行了仿真,结果显示,Bob发射天线和接收天线数量的安排对Eve的误比特率和窃听信道容量有明显的影响.当Bob发送人工噪声的天线数量不低于Eve天线数量时,人工噪声能对Eve形成有效的干扰,可明显降低其接收性能,可达保密速率随发送功率增加而持续增加. Bob最优的发送和接收天线数量分配方案应是配置与Eve天线数相同的发送天线,此时Eve不能有效地抑制干扰,同时又能兼顾Bob的接收性能,能获得最佳的安全传输性能.
| [1] |
Goel S, Negi R. Guaranteeing secrecy using artificial noise[J]. IEEE Transactions on Wireless Communications, 2008, 7(6): 2180-2189. |
| [2] |
Li Wei, Ghogho M, Chen Bin, et al. Secure communication via sending artificial noise by the receiver:outage secrecy capacity/region analysis[J]. IEEE Communications Letters, 2012, 16(10): 1628-1631. |
| [3] |
Zheng Gan, Krikidis I, Li Jiangyuan, et al. Improving physical layer secrecy using full-duplex jamming receivers[J]. IEEE Transactions on Signal Processing, 2013, 61(20): 4962-4974. |
| [4] |
Masood M, Ghrayeb A, Babu P, et al. A minorization-maximization algorithm for maximizing the secrecy rate of the MIMOME wiretap channel[J]. IEEE Communications Letters, 2017, 21(3): 520-523. |
| [5] |
Li Lingxiang, Chen Zhi, Zhang Duo, et al. A full-duplex bob in the MIMO Gaussian wiretap channel:scheme and performance[J]. IEEE Signal Processing Letters, 2016, 23(1): 107-111. |
| [6] |
Guo Tianwen, Wang Baoyun, Wu Wei, et al. Secrecy-oriented antenna assignment optimization at full-duplex receiver with self-interference[J]. IEEE Wireless Communications Letters, 2018, 7(4): 562-565. |
| [7] |
Anitha M, Kurahatti N G. Adaptive beamforming using neural network and fuzzy logic model for measurement data fusion[C]//2015 International Conference on Communications and Signal Processing (ICCSP). New York: IEEE Press, 2015: 209-214.
|
| [8] |
Sallomi A H, Ahmed S. Multi-layer feed forward neural network application in adaptive beamforming of smart antenna system[C]//2016 Al-Sadeq International Conference on Multidisciplinary in IT and Communication Science and Applications (AIC-MITCSA). New York: IEEE Press, 2016: 1-6.
|
| [9] |
桂冠, 王禹, 黄浩. 基于深度学习的物理层无线通信技术:机遇与挑战[J]. 通信学报, 2019, 40(2): 19-23. Gui Guan, Wang Yu, Huang Hao. Deep learning based physical layer wireless communication techniques:opportunities and challenges[J]. Journal on Communications, 2019, 40(2): 19-23. |
| [10] |
Song Huanhuan, Wen Hong, Hu Lin, et al. Secure cooperative transmission with imperfect channel state information based on BPNN[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10482-10491. |
| [11] |
Haykin S. Neural network and machine learning (Third Edition)[M]. New York: Pearson Education, Inc., 2009: 91-117.
|



