2. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 西安 710071
为了优化空间耦合低密度奇偶校验(SC-LDPC)码在加性高斯白噪声信道下的性能,改变了其边缘扩展规则,将规则SC-LDPC码原模图上变量节点的边连接到与其相对应的前一个位置的校验节点上,提出了一种新型的空间耦合结构.对其基矩阵、码率、度分布及译码复杂度进行分析,结果表明,与传统的SC-LDPC码相比,链长相同时,新结构的码率有所提高,校验节点的度分布变大.最后通过BP译码验证了提出的空间耦合新结构译码性能的优越性.
2. State Key Laboratory of Integrated Services Networks, Xidian University, Xi'an 710071, China
In order to optimize the performance of spatially coupled low density parity check (SC-LDPC) codes over the additive white gaussian noise channel, a novel spatial coupling structure was proposed by changing the edge spreading rules, the edges of the variable nodes were connected to the check nodes of the previous position. Basis matrix, rate, degree distribution and computational complexity were analyzed and the results show that the rate of the novel structure is promoted with the degree distribution of check nodes become larger. Finally, the performance of the proposed novel structure is verified by BP decoding.
空间耦合低密度奇偶校验(SC-LDPC,spatially coupled low density parity check)码是一类可以逼近容量限的码字,Kudekar等[1-2]证明了其置信传播译码门限能够达到对应规则LDPC码的最大后验概率译码门限.然而,此种渐进性能只存在于无限长的码字结构中,当耦合链长有限时,性能损失问题以及末端额外的校验节点造成的码率损失问题就会凸显出来.
前人对SC-LDPC码进行结构设计,在减少其码率损失或提高其性能方面做了相关研究. Sanatkar等[3]提出了使用非规则的度分布在边界添加额外的变量节点提高SC-LDPC码的速率. Kwak等[4]通过在可靠位置添加变量节点构造的码字结构,减少码率损失的同时保证了有限长度时的译码性能.随后,Kwak等[5]又提出了一种利用线性规划设计的度分布不均匀的非规则SC-LDPC码,其渐进性能以及有限长度下的性能均优于规则SC-LDPC码. Chen等[6]通过联合优化空间耦合长度与非耦合长度,最小化了由有限码字长度引起的SC-LDPC码的性能损失.
笔者在传统规则SC-LDPC码的基础上提出了一种新型的耦合结构,该结构定义了一种新的边缘扩展方式,允许原模图中变量节点的边连接到与其相对应的前一个位置的校验节点上,相应减少了校验节点的数量,从而降低了码率损失,同时增大了少数校验节点的度分度.通过对译码复杂度的分析与数值仿真,在加性高斯白噪声(AWGN, additive white gaussian noise)信道模型下验证了所提出的新型SC-LDP码耦合结构的译码性能优于传统规则的SC-LDPC码.
1 SC-LDPC码构造SC-LDPC码与构造原模图LDPC码[7-8]类似,将结构优异的规则LDPC码原模图单元复制、置换,最终可得到一个空间耦合链结构,即将L个度分布为规则(l, r)LDPC码原模图单元耦合起来可得到一个(l, r, L, w)SC-LDPC码原模图.其中,符号L表示SC-LDPC码空间耦合链的链长,l和r分别表示变量节点与校验节点的最大度数,w表示耦合宽度,与此原模图相对应的基矩阵用符号B表示.在SC-LDPC码的原模图中每个变量节点、每个校验节点和每条边分别对应着Tanner图中M个变量节点、M个校验节点和M条边,即在基矩阵中,每个1元素用M×M阶的二元置换矩阵替换,每个0元素用M×M阶的全零矩阵替换,M称为扩展因子.
要构造具有特定度分布的(l, r)SC-LDPC码(只考虑r是l倍数的情况),首先需要找到性能良好规则的(l, r)LDPC原模图,确定SC-LDPC码的原模图单元,令gcd (l, r)代表l和r的最大公约数,则原模图单元中变量节点的数目为r/gcd (l, r),校验节点的数目为l/gcd (l, r)[9].确定原模图单元后,根据选择的链长L进行复制,将复制后每个位置上连接变量节点与校验节点的边展开,依次均匀独立地连接到不同位置的校验节点上,此过程中为了完成空间耦合需要添加额外的校验节点.具体的边缘扩展方式如下:位置u处的变量节点依次与位置u, u+1, …, u+l-1处的校验节点相连,由此可知耦合宽度w = l-1,即为了完成空间耦合,末端需要增加l-1个校验节点.以规则(3, 6)SC-LDPC码为例,采用边缘扩展的方法进行空间耦合的过程细节如图 1所示,圆圈v表示变量节点,正方形c表示校验节点,L表示链长,为了完成空间耦合,额外添加了w = 3-1 = 2个校验节点.

|
图 1 规则(3, 6)SC-LDPC码构造过程 |
若SC-LDPC码的链长为L、耦合宽度为w,则SC-LDPC码的基矩阵为
| $ {\mathit{\boldsymbol{B}}_{[0, L - 1]}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_0}}&{}&{}&{}\\ {{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_0}}&{}&{}\\ \vdots &{{\mathit{\boldsymbol{B}}_1}}& \ddots &{}\\ {{\mathit{\boldsymbol{B}}_w}}& \vdots & \ddots &{{\mathit{\boldsymbol{B}}_0}}\\ {}&{{\mathit{\boldsymbol{B}}_w}}&{}&{{\mathit{\boldsymbol{B}}_1}}\\ {}&{}& \ddots & \vdots \\ {}&{}&{}&{{\mathit{\boldsymbol{B}}_w}} \end{array}} \right]_{\left( {L + w} \right){b_c} \times L{b_v}}} $ | (1) |
其中每个元素均对应一个大小为bc×bv的子块Bi, i = 0~w,故码率可表示为
| $ R = 1 - \frac{{\left( {L + w} \right){b_c}}}{{L{b_v}}} $ | (2) |
当图 1中的耦合链长L = 7时,由图 1(b)可知,每个位置上的变量节点均匀独立地与3个校验节点相连,处于耦合链开始和结尾处的校验节点与2个或4个变量节点相连,中间位置的校验节点均匀独立地与6个变量节点相连,因此对应的基矩阵可表示为
| $ \mathit{\boldsymbol{B}} = \left[ \begin{array}{l} 11000000000000{\rm{ }}\\ 11110000000000{\rm{ }}\\ 11111100000000{\rm{ }}\\ 00111111000000{\rm{ }}\\ 00001111110000{\rm{ }}\\ 00000011111100{\rm{ }}\\ 00000000111111{\rm{ }}\\ 00000000001111{\rm{ }}\\ 00000000000011 \end{array} \right] $ | (3) |
在构造SC-LDPC码的过程中,为了满足空间耦合条件,需要额外添加w = l-1个校验节点,本节通过改变边的展开规则,只需要额外添加l-2个校验节点便可以完成空间耦合.在构造新结构的过程中耦合宽度w = l-1不变,处于位置0处的变量节点的边依次均匀独立地与位置1, 2, …, l处的校验节点相连,处于位置u(u≥1)处的变量节点的边分别与位置u-1, u, …, u+l-2处的校验节点相连,因此校验节点末尾只需要添加l-2个校验节点.在本节仍以规则(3, 6)SC-LDPC为例,图 2直观地展示了新结构进行空间耦合时边的连接过程.
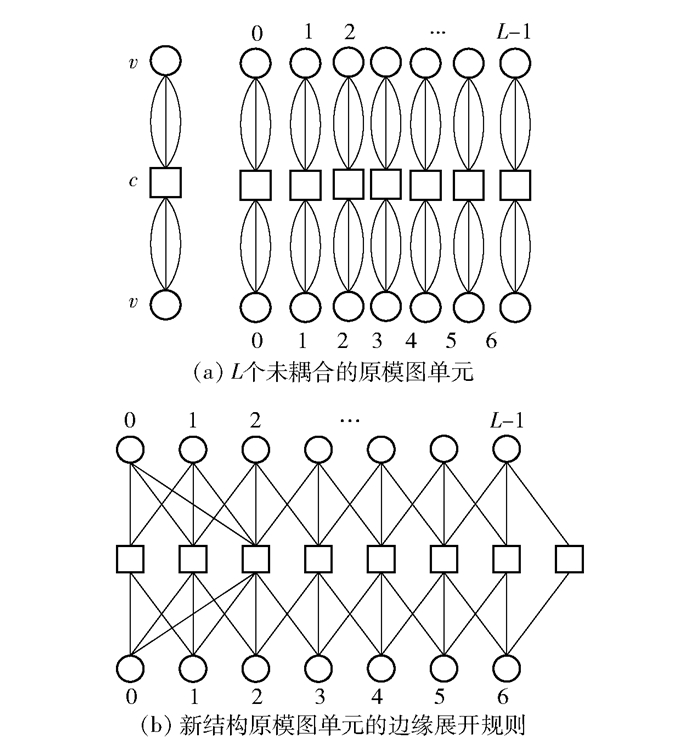
|
图 2 SC-LDPC码新结构的构造过程 |
若SC-LDPC码的新结构链长为L、耦合宽度为w,则其基矩阵为
| $ {\mathit{\boldsymbol{B}}_{[0,L - 1]}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_0}}&{{\mathit{\boldsymbol{B}}_0}}&{}&{}&{}&{}\\ {{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_0}}&{}&{}&{}\\ \vdots & \vdots &{{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_0}}&{}&{}\\ {{\mathit{\boldsymbol{B}}_w}}&{{\mathit{\boldsymbol{B}}_w}}& \vdots &{{\mathit{\boldsymbol{B}}_1}}& \ddots &{}\\ {}&{}&{{\mathit{\boldsymbol{B}}_w}}& \vdots & \ddots &{{\mathit{\boldsymbol{B}}_0}}\\ {}&{}&{}&{{\mathit{\boldsymbol{B}}_w}}&{}&{{\mathit{\boldsymbol{B}}_1}}\\ {}&{}&{}&{}& \ddots & \vdots \\ {}&{}&{}&{}&{}&{{\mathit{\boldsymbol{B}}_w}} \end{array}} \right]_{\left( {L + w - 1} \right){b_c} \times L{b_v}}}$ | (4) |
其中每个元素Bi, i = 0~w均对应一个大小为bc×bv的子矩阵.新结构减少了校验节点的数量,如基矩阵的下标所示,校验节点数目的减少对应着行数的减少,故码率可表示为
| $ R = 1 - \frac{{\left( {L + w - 1} \right){b_c}}}{{L{b_v}}} $ | (5) |
当图 2中的耦合链长具体为L = 7时,每个变量节点均匀独立地与3个校验节点相连,位于耦合链开始处的校验节点与4个变量节点相连,结尾处的2个校验节点分别与4个和2个变量节点相连,位于耦合链第3个位置的校验节点与8个变量节点相连,其他位置的校验节点均匀独立地与6个变量节点相连.现在变量节点的度最大为3,校验节点的度最大为8,对应的基矩阵为
| $ \mathit{\boldsymbol{B}} = \left[ \begin{array}{l} 11110000000000{\rm{ }}\\ 11111100000000{\rm{ }}\\ 11111111000000{\rm{ }}\\ 00001111110000{\rm{ }}\\ 00000011111100{\rm{ }}\\ 00000000111111{\rm{ }}\\ 00000000001111{\rm{ }}\\ 00000000000011 \end{array} \right] $ | (6) |
传统SC-LDPC码的码率在耦合链长趋于无限时可近似认为等于规则LDPC原模图单元的码率.然而,当耦合链长为有限长度时,就会存在因在末端添加校验节点造成的码率损失问题.第2节介绍的SC-LDPC码新结构在耦合的过程中改变了边缘扩展规则,相应地减少了在末端添加校验节点的数量,即传统的SC-LDPC码需要添加l-1个校验节点,新结构只需添加l-2个校验节点.由式(2)和式(5)给出的码率表达式可以看出,码率与耦合链长L、耦合宽度w以及子矩阵的大小有关,在耦合链长较短时,所提出的空间耦合新结构能够有效地减少码率的损失.
3.2 复杂度分析SC-LDPC码译码时,计算复杂度不仅与选取的链长L、扩展因子M有关,还与变量节点和校验节点的度分布有关.在每个位置上都有2M个变量节点,M个校验节点,先依次更新每个位置上度分布为l的变量节点,再依次更新每个位置上度分布为r的校验节点,此时,SC-LDPC码译码迭代一次的计算复杂度可以表示为
| $ {C_{\rm{T}}} = \left( {2MlL} \right)\left( {MrL} \right) = 2rl{L^2}{M^2} $ | (7) |
所提出的新结构与传统结构相比列重相同,行重略有变化.以耦合链长L = 7的(3, 6)规则LDPC码原模图单元构造SC-LDPC码为例,由式(3)与式(6)可以看出(3, 6)规则SC-LDPC码和其新结构的列重均为3,最大行重分别为6和8.行重值变大,意味着参与校验方程的变量节点增多,更多的变量节点受到保护,可以改善译码性能.然而,由于新结构中少量校验节点的度增加,所以计算复杂度略微增加.
4 仿真结果下面分别选取不同参数下同码长同码率的规则(3, 6) SC-LDPC码与SC-LDPC码的新结构进行性能仿真,结果如图 3和图 4所示,虚线表示规则(3, 6) SC-LDPC码,实线表示新结构.在图 3中,规则(3, 6) SC-LDPC码的链长L分别为30、40、50,对应的二元置换矩阵的阶数M分别为50、300、1000;新结构的链长L分别为15、20、25,阶数M分别为100、600、2 000.此时,得到了码率R为0.467、码长n为3 000的短码,码率R为0.475、码长n为24 000的中长码以及码率R为0.48、码长n为100 000的长码.在图 4中,规则(3, 6) SC-LDPC码的链长L全部为30,对应的阶数M分别为50、200、1 500;空间耦合新结构的链长L全部为15,阶数M分别为100、400、3 000.此时,得到的3组码字,码率R均为0.467,码长n分别为3 000、12 000、90 000.

|
图 3 3组不同码率的SC-LDPC码性能比较 |

|
图 4 3组相同码率的SC-LDPC码性能比较 |
由图 3可以看出,在3组同码长同码率的码字中,所提出的SC-LDPC新结构的译码性能均优于同组的规则(3, 6) SC-LDPC码.新结构与规则(3, 6) SC-LDPC码相比,码长n为3 000时,原结构在信噪比为2.6 dB、误码率为10-4时开始出现错误平层,新结构则在信噪比为2.3 dB时误码率达到10-6,大约有2 dB的增益;码长n为24 000且误码率为10-6时,新结构比原结构大约有0.05 dB的增益;码长n为100 000且误码率为10-6时,新结构比规则(3, 6) SC-LDPC码大约有0.03 dB的增益. 图 4中的3组码字码率全部相同,新结构与规则(3, 6) SC-LDPC码相比,在码长n为12 000且误码率为10-6时大约有0.3 dB的增益,码长n为90 000且误码率为10-6时仍有微小的增益.
从上面的分析中得知,所提出的SC-LDPC码的新结构对短码、中码、长码均适用,是一类译码性能优异的码字,尤其对短码的译码性能改善最佳,因此新结构更适用于AWGN信道中短码的传输.
5 结束语笔者通过对传统SC-LDPC码进行边的重排,构造出一种新的空间耦合结构.该结构从本质上减少了需要额外添加的校验节点的数量,使码字更进一步地趋向于未耦合时的码率,降低了码率的损失.与传统的SC-LDPC码相比,该结构增加了变量节点之间的约束关系.最后仿真结果证明,所提出的新结构,在AWGN信道下,可以改善传统SC-LDPC码的译码性能并且对改善短码的错误平层效应尤为突出.
| [1] |
Kudekar S, Richardson T J, Urbanke R L. Threshold saturation via spatial coupling:why convolutional LDPC ensembles perform so well over the BEC[J]. IEEE Transactions on Information Theory, 2011, 57(2): 803-834. |
| [2] |
Kudekar S, Richardson T J, Urbanke R L. Spatially coupled ensembles universally achieve capacity under belief propagation[J]. IEEE Transactions on Information Theory, 2013, 59(12): 7761-7813. DOI:10.1109/TIT.2013.2280915 |
| [3] |
Sanatkar M R, Pfister H D. Increasing the rate of spatially-coupled codes via optimized irregular termination[C]//2016 9th International Symposium on Turbo Codes and Iterative Information Processing (ISTC). Brest: IEEE Press, 2016: 31-35.
|
| [4] |
Kwak H, Kim J, Jong-Seon. Rate-loss reduction of SC-LDPC codes by optimizing reliable variable nodes via expected graph evolution[C]//2017 IEEE International Symposium on Information Theory (ISIT). Aachen: IEEE Press, 2017: 2930-2934.
|
| [5] |
Kwak H, No J, Park H. Design of irregular SC-LDPC codes with non-uniform degree distributions by linear programming[J]. IEEE Transactions on Communications, 2019, 67(4): 2632-2646. DOI:10.1109/TCOMM.2018.2889850 |
| [6] |
Chen Shuang, Peng Kewu, Zhang Yushu, et al. Optimization of finite-length SC-LDPC for uplink NOMA[C]//2018 IEEE International Conference on Communications Workshops (ICC Workshops). Kansas City, MO: IEEE Press, 2018: 1-6.
|
| [7] |
Thorpe J. Low-density parity-check (LDPC) codes constructed from protographs[J]. Interplanetary Network Progress Report, 2003, 42(154): 1-7. |
| [8] |
Divsalar D, Dolinar S, Jones C. Constructions of protograph LDPC codes with linear minimum distance[C]//2006 IEEE International Symposium on Information Theory. Seattle, WA: IEEE Press, 2006: 664-668.
|
| [9] |
Mitchell D G M, Lentmaier M, Costello D J. Spatially coupled LDPC codes constructed from protographs[J]. IEEE Transactions on Information Theory, 2015, 61(9): 4866-4889. DOI:10.1109/TIT.2015.2453267 |



