2. 电子科技大学 自动化工程学院, 成都 611731
针对微电网中能源调度的经济效益、充电效率优化、系统负荷波动以及碳排放问题,提出将强化学习运用到微电网调度中,通过建立一个完整的微电网模型,使强化学习在不断迭代过程中得到最优策略,同时达到经济效益趋向最大化、充电功率相对稳定、系统负荷波动减少、碳排放量达到最小化这4个联合优化目标.仿真结果表明,采用的控制策略既能很好地实现经济效益最大化收敛、碳排放量最小化收敛,同时又能使得充电功率相对稳定,微电网的负荷也能减少,极大地提高了系统的稳定性.
2. School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
Aiming at the economic benefit problem, charging efficiency optimization problem, system load fluctuation problem and carbon emissions problem of energy scheduling in microgrid, application of reinforcement learning to energy scheduling in microgrid is presented. By establishing a complete microgrid model and using reinforcement learning to obtain the optimal strategy in the continuous iterative process, economic benefits tended to be maximized, charging power is relatively stable, load fluctuation of the system is reduced, and carbon emissions is tended minimized. These four joint optimization objectives are reached. Simulations show that the control strategy used in this system can not only maximize the convergence of economic benefits and minimize carbon emissions, but also make the charging power relatively stable, and reduce the load of microgrid. The stability of this system will be improved greatly.
随着电网技术不断进步,微电网逐渐成为复杂的独立系统,与大电网的主要差别在于,其既可以作为独立的系统运行,也可以接入大电网协同运行.微电网运行最主要的特点是可以连接各种能源系统,以达到最优的运行效率[1-2],所以将不同的能源系统并入到一个微电网中进行能源调度并且优化其控制策略,成为当前热门的一个研究课题[3-5].
关于系统建模问题,在能源互联网框架下,鞠平等[3]提出了高比例新能源并网的概念,Roberts[6]提出了将多种能源相结合(电、热、气等),他们虽然将能源的框架描述的比较详细,但并没有将多种能源并入到微电网中详细地进行数学建模分析.
具体到能源建模方面来看,徐丰[7]描述了光伏发电的建模过程,周围等[8]用4种数学表达公式描述了风的随机性和波动性,他们对于清洁能源均进行了非常详细的数学建模;刘国静等[9]运用风储的技术来稳定电网的功率,钟伟峰[10]和周文辉等[11]利用电动汽车来对电网的负荷进行削峰填谷,他们均是利用其他能源对微电网进行干预来稳定功率.笔者将侧重描述一个较为完整的微电网,并针对其负荷波动以及充电功率的稳定性来做深入研究.
在上述背景下描述的是一个比较庞大且复杂的微电网,在这个模型上采用传统的算法会使得能源调度难以找到最优化路径,并且耗时会相对较长,同时微电网中也存在很多不确定性.对于这些问题,强化学习中的Q学习就能够很好地解决[12].笔者在模型的构建上,将连续的时间离散化,建立模型矩阵,并且与强化学习中的Q学习结合,这将有利于解决微电网能源调度这个复杂的问题. Etemad等[13]建立了关于风能与光伏能的模型,并采用Q学习的方法寻找最合适的调度方式. Wu等[14]描述的是一个电动汽车混合能源调度的场景,采用了深度强化学习的方法解决了经济规划问题以及多维度问题.所以使用强化学习,能够解决很多复杂的非线性问题,这对于复杂的微电网而言是一种较为合理的算法,但对于解决多维度问题,传统强化学习仍然存在着计算复杂、迭代次数过多等缺点,因此,合理地改进强化学习也是当前研究的热点.
综上所述,在模型的层面上,上述论文中对于模型的建立虽然比较详细具体,但却停留在单独的系统,没有考虑整体微电网中多个系统的相互影响、相互耦合、相互协调的关系.笔者建立的微电网包含了风能、光伏能、电动汽车模型、储能系统模型等,将各种能源协调在一起,符合当前时代多能源这一趋势;在实现目标上,不仅仅有经济效益这一目标,还对能源的相互协调、系统的负荷波动进行了优化,同时减少碳排放量;在算法方面,使用了当前比较常用的智能算法——强化学习中的Q学习算法,其核心是对模型进行不停迭代寻找最优策略,并且在此基础上进行了改进,加入了数据集,使得算法有了记忆功能,减少了迭代次数,同时引入了贪婪算法,使得强化学习的探索更为全面.
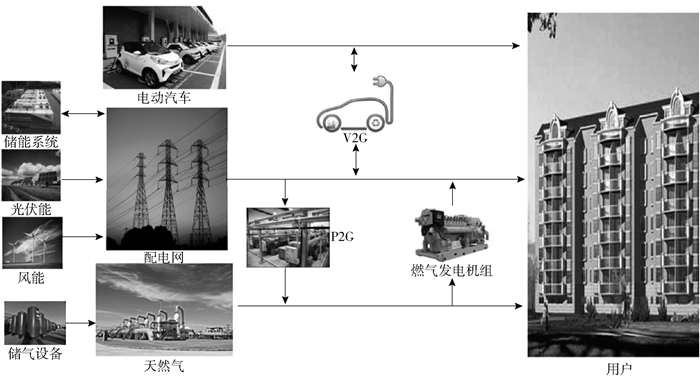
1 系统建模系统模型如图 1所示.该微电网描述的是一个针对住宅区的独立网络,其由配电网、分布式的能源系统(风能、太阳能)、储能系统、天然气设备、能源载体电动汽车、能源转换设备和用户群体构成,其中配电网与大电网相连接,其电量储备来自大电网的调度.在微电网体系中引入了P2G(power to gas)、V2G(vehicle to grid)等能源转换模型,以此描述出了一个较为复杂的微电网模型. P2G在微电网中的运用是通过将水电解后生成甲烷送入天然气网络,使得能量在电力系统和天然气系统之间的流动成为可能,进而增加了系统运行的灵活性. V2G在微电网中的运用是在白天鼓励将闲置汽车的电充入配电网中来应对用电高峰期,降低了高峰期的用电负荷,在晚上配电网供电给电动汽车中储备,节省了电能的损耗.风能、光伏能、储能系统是用于供电给配电网的,其模型也会根据时间、天气、地点的不同发生改变,系统也会进行筛选并进行充电.最终这些能源的流向是用户(这里的用户泛指用电的居民).
|
图 1 微电网模型 |
在所设计的系统中,通过风力发电为配电网提供能源,在模型中,风速越大,提供的功率也就越大.风速在自然中表现出随机性与波动性,为形象地表现出其物理特性,在本系统采用一天中随机模拟阵型风和渐变风来表征其状况.
1) 阵型风.阵型风作为风力模型中风速在某时刻发生突变的分量,在仿真系统中常使用三角函数公式来表征其特性,即
| $ V_{{\rm{ wind }}}^t = \left\{ {\begin{array}{*{20}{l}} {0,}&{t < {T_{{\rm{ as }}}}}\\ {\frac{{{V_{{\rm{ amax }}}}}}{2}}&{\left[ {1 - {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\pi \left( {\frac{{t - {T_{{\rm{ as }}}}}}{{{T_{\rm{w}}}}}} \right)} \right],\quad {T_{{\rm{as}}}} \le t < {T_{{\rm{ ae }}}}}\\ {0,}&{t \ge {T_{{\rm{ ae }}}}} \end{array}} \right. $ | (1) |
其中:Vwindt、Vamax、Tas、Tae分别为风速(m/s)、峰值(m/s)、起始时刻和终止时刻.
2) 渐变风.渐变风作为风力模型中风速随时间线性变化的分量,用来表征风力的渐变特性,表达式为
| $ V_{{\rm{ wind }}}^t = \left\{ \begin{array}{l} 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t < {T_{{\rm{ bs }}}}\\ {V_{{\rm{ amax }}}}\frac{{t - {T_{{\rm{ bs }}}}}}{{{T_{{\rm{ bs2 }}}} - {T_{{\rm{ bs }}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{{\rm{ bs }}}} \le t < {T_{{\rm{ bs2 }}}}\\ {V_{{\rm{ amax }}}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{{\rm{ bs2 }}}} \le t < {T_{{\rm{ be }}}}\\ 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t \ge {T_{{\rm{ be }}}} \end{array} \right. $ | (2) |
其中:Tbs、Tbs2、Tbe分别为起始渐变时刻、起始保持不变时刻和终止时刻.
在所设计的光伏发电模型中,光照强度直接决定光伏发电的强弱,同时光照强度是以正午光照强度最强的正态分布,并且光照强度也会受到风速的影响,风速越大,光照强度会相对减少.
| $ S_{{\rm{pv}}}^t = \frac{1}{{\sqrt {2\pi } \sigma }}{{\rm{e}}^{\frac{{ - {{(t - \mu )}^2}}}{{2{\sigma ^2}}}}} - \rho V_{{\rm{wind}}}^t $ | (3) |
其中:μ、σ、ρ为系数,Spvt为实际的光照强度.
1.2 优化目标系统考虑优化如下几个目标.
第1个目标是经济效益目标,在微电网中进行状态转换的同时,会伴随着经济效益的变化,通过强化学习迭代出最优调度策略使得经济效益最大化.
| $ \begin{array}{*{20}{l}} {{\rm{max}}C(t) = \sum\limits_{t = 1}^T ( dR_{{\rm{grid}}}^t + bR_{{\rm{vehicle}}}^t + cR_{{\rm{gas}}}^t - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({a_2}C_{{\rm{grid}}}^t + {b_2}C_{{\rm{gas}}}^t) + r_{{\rm{con}}}^t)} \end{array} $ | (4) |
其中:Rgridt、Rvehiclet、Rgast分别为配电网放电、电动汽车放电、天然气系统供气给用户所带来的收益;d、b、c为系数;Cgridt、Cgast为配电网从储能系统购电、天然气系统从储气系统中购气的价格成本;d2、b2为系数;rcont为能源相互转换系统给的奖励值.
第2个目标是微电网系统能源的相互协调以及充电功率的优化问题,见式(5)~式(8).其中配电网的充电包括从储能系统中充电、风能充电、光伏能充电3种方式.因为风能与光伏能属于波动较大的能源,如果储能系统采用恒定的功率,整个微电网的充电功率就会有所波动,但如果能够对储能系统的功率加以控制,就能使得微电网的充电功率相对稳定.
| $ {P_{{\rm{ charge }}}^t = P_{{\rm{ storage }}}^t + P_{{\rm{ wind }}}^t + P_{{\rm{pv}}}^t} $ | (5) |
| $ {P_{{\rm{ min }}}^t < P < P_{ {\rm{max}} }^t} $ | (6) |
| $ {P_{{\rm{min\_s}}}^t < P_{{\rm{ storage }}}^t < P_{{\rm{max\_s}}}^t} $ | (7) |
| $ {{\rm{min}}(P_{{\rm{ storage }}}^tP_{\rm{e}}^t + C_{{\rm{ wind }}}^t + C_{{\rm{ pv }}}^t)} $ | (8) |
其中:Pmint、Pmaxt为整个充电功率的上下限,Pstoraget、Pwindt、Ppvt分别为储能系统、风能、光伏能的充电功率,Pcharget为微电网总充电功率,Pmin_st、Pmax_st为储能系统充电功率的上下限,Pet为成本电价,Cwindt、Cpvt分别为风力发电和光伏发电的成本费用.
第3个目标是系统的负荷优化问题,过高的负荷会对微电网稳定性造成影响,加速电力设备老化,通过电动汽车对系统负荷进行削峰填谷,使得整个系统的负荷波动减小.随着充电负荷的增加,负荷压力成指数上升,总负荷压力表述为
| $ {p_{{\rm{ grid }}}^t = p_{{\rm{ charge }}}^t - p_{{\rm{ discharge }}}^t + p_{{\rm{ convert }}}^t} $ | (9) |
| $ {{P_{{\rm{sys\_min}}}} < P_{{\rm{ grid }}}^t < {P_{{\rm{sys\_max}}}}} $ | (10) |
| $ {P_{{\rm{ grid }}}^t = P_{{\rm{ grid }}}^t + \gamma P_{{\rm{ stable }}}^t} $ | (11) |
| $ {h(t) = {\rm{exp}}[\mu P_{{\rm{ grid }}}^t]} $ | (12) |
其中:μ、γ为常系数,Pgridt为微电网总负荷,Psys_min、Psys_max分别为微电网系统总负荷的上下限, Pstablet为电动汽车削峰填谷的功率变化,Pcharget为其他能源(风能、光伏能和储能系统)向配电网供电的功率,Pdischarget为配电网放电给用户总功率,Pconvertt为配电网与其他系统交互的总功率.
第4个目标是碳排放量的问题,过多碳排放量会对环境造成巨大的影响,不利于舒适宜居的居住环境.在本系统中,每次状态转移都会伴随着碳排放量的变化,假定电动汽车与风能、光伏能的碳排放量较少,通过强化学习迭代得出相对碳排放量较少的调度路线,平均每小时碳排放量表示为
| $ \begin{array}{*{20}{l}} {C_{{\rm{ average }}}^t = \sum\limits_{t = 1}^T {(C_{{\rm{grid\_em}}}^t + C_{{\rm{ vehicle }}}^t + C_{{\rm{gas\_em}}}^t + {C_1}(} P_{{\rm{ storage }}}^t + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_2}{\rm{ln}}(P_{{\rm{ wind }}}^t + {C_3}P_{{\rm{pv}}}^t)))/t} \end{array} $ | (13) |
其中:Caveraget为总的碳排放量;Cgrid_emt、Cgas_emt、Cvehiclet分别为配电网、天然气、电动汽车系统的碳排放量,3种变量与各自的效率均有关联,如配电网的碳放量Cgrid_emt = -agridPgridt+bgrid(agrid、bgrid为系数);C1、C2、C3皆为系数.
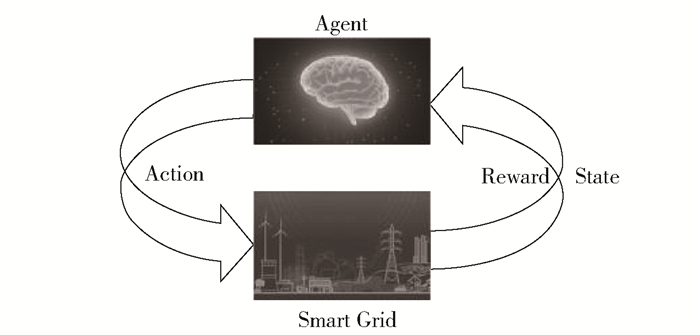
2 基于Q学习的决策 2.1 Q学习算法Q学习算法是目前强化学习中使用较为普遍的算法之一,主要是通过奖励或惩罚来学习怎样选择能产生最大积累奖励的行动算法.如图 2所示,Q学习中Agent相当于是整个算法的大脑,通过不停的试错分析出最佳的行为,并反馈给当前的环境(也就是微电网(smart grid)),当前环境收到并实施了该行为后,会有相对应的状态(state)转换并伴随着利益值(reward)的增加,同时也反馈给Agent,因此形成了闭环控制.
|
图 2 Q学习过程 |
Q学习的核心算法具体如下:
| $ \begin{array}{*{20}{c}} {Q({S_t},{A_t}) = Q({S_t},{A_t}) + \alpha [{R_{t + 1}} + }\\ {\lambda {\kern 1pt} {\kern 1pt} \mathop {{\rm{max}}}\limits_a Q({S_{t + 1}},a) - Q({S_t},{A_t})]} \end{array} $ | (14) |
其中:S为微电网的状态;A为微电网的决策行为,包含了充放电、与其他能源进行能源交互等;Q(St, At)为目标优化函数;α为学习步长;λ为折扣因子;R(St, At)为该状态St以及该行为At所产生的回报值;
在初始化Q值表中,会有预处理的过程,传统的Q学习都是以一个全新的矩阵作为初始矩阵来进行迭代的,而本系统中预处理的具体方法是将以往得到的环境变量和Q值表保存并且形成一个数据集,在这一次的Q学习中将根据当前的环境数值,从数据集中匹配选取最合适的Q值表作为初始矩阵,这样可以减少迭代次数,减少程序运行的时间.
在迭代过程中,一般采用的是贪婪策略:
| $ {\pi ^*}(s) = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{max}}}\limits_{a \in A} Q({S_t},{A_t}) $ | (15) |
该策略的具体操作是在执行动作时,有大概率可能性执行最优的策略,但也有小概率可能去尝试不是最优的策略,这样当试验次数够多时,可以遍历每一种方法,既能够在一定程度上对已经探索过的最优选择进行保留,又能够对未知的选择进行探索试错,使得整个算法更加完善.
2.2 能源调度的Q学习过程模型的建立是一个马尔可夫的决策过程,将原本连续的微电网运作过程离散化,以配电网电池储存电量、储气能、电动汽车储电能、时间作为系统状态,以充放电、电能互相转换作为动作策略,如当前状态St,经允许的动作策略a,就能够转移到下一个状态St+1,并伴随着效益等参数的变化.
首先,要确定Q(S, A)中的状态S和动作策略A,在本系统中配电网储电量等级E、电动汽车储电量等级O、天然气储气量等级G和时间t作为状态输入,其中将时间状态量离散成24个时段,将配电网储电量、电动汽车储电量、天然气储气量离散为区间的形式,各区间Δp可表示为
| $ \Delta p = \frac{{{p_{{\rm{max}}}} - {p_{{\rm{min}}}}}}{M} $ | (16) |
可知存在着
确定动作策略a时,不同的状态量有着不同的动作策略.首先,以微电网里的配电网为例,其自身有着充放电等动作,其电量储备来自大电网.假设-1和+1表示配电网储电量等级的变化,配电网中的电量可以通过P2G及V2G与天然气、电动汽车等其他能源进行交互,配电网的动作策略合集为
| $ A = \left\{ \begin{array}{l} - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{配电网}} \to {\rm{电动汽车}}\\ + 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{配电网}} \leftarrow {\rm{电动汽车}}\\ - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{配电网}} \to {\rm{天然气}}\\ + 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{配电网}} \leftarrow {\rm{天然气}}\\ + 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{配电网}} \leftarrow {\rm{储能系统等}}\\ - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{配电网}} \to {\rm{用户}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\ {\rm{闲置}} \end{array} \right. $ | (17) |
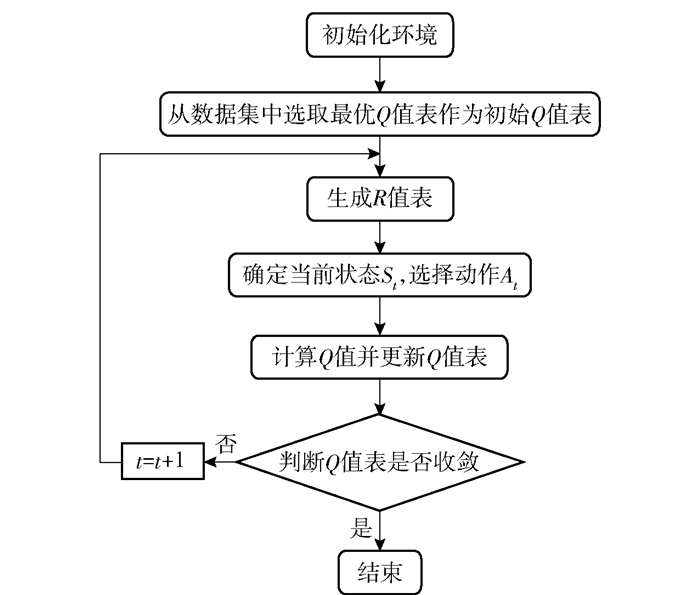
在确定输入状态和动作策略之后,即可进行在线学习,通过Q算法的不停迭代,每次将该状态迭代得到的新数值记录在一个矩阵中,这个矩阵就叫作Q值表,最终能够让Q值表趋向于收敛,从而找出最优的调度路线,学习流程如图 3所示.
|
图 3 学习流程 |
步骤1 初始化环境.
步骤2 根据当前的环境等变量,从数据集中选取最合适的Q值表作为初始Q值表.
步骤3 根据选择的环境(工业区或者居民区、夏季或者冬季)、当前时间的电价、天然气价等变量来计算各个状态转换得到的利益值或者奖励值,并填入该状态相对应动作的R矩阵中,如果R矩阵中该状态没有相对应的动作,在矩阵中用-inf表示,由此可以生成R值表.
步骤4 根据当前的状态St,即配电网储电量、电动汽车储电量、天然气储气量、当前时间,确定该状态能够采取的动作行为At,使之能够进行状态转移到St+1.
步骤5 采用上述的Q算法公式并结合贪婪算法,选择对应的策略并更新Q值.
步骤6 判断Q值表是否收敛,如果是则结束迭代并在数据集中记录环境数值和对应的Q值表,不是则返回步骤3.
3 仿真结果与分析模拟仿真中,假定配电网储电量为7.5 MW·h,将其以2.5 MW·h为间隔划分为4个能量等级;电动汽车的总储电量为3 MW·h,将其以1 MW·h为间隔划分为4个能量等级;储气罐中的储气量为15万m3,将其以5万m3为间隔划分为4个能量等级;将一天的时间划分为24 h各时段,即一共有43×24 = 1 536种状态.
关于策略动作,以配电网为例,每一种状态最多有着共计5种动作行为,包括闲置、配电网的充放电、天然气系统和电动汽车系统的交互.另外,天然气系统和电动汽车系统自身可以供气、供电给用户.当配电网供电给其他设备时,配电网储电量等级为-1;反之其他设备充电给配电网时,配电网储电量等级为+1.配电网的充放电功率最大允许值是2.5 MW.
环境设定上,关于光伏能的数学建模是以正午光照强度最大的正态分布,转换为电能的效率为:0.15≤η1≤0.25,光伏能转换为电能的最大功率为0.5 MW.关于风能的数学建模是随机生成基于正弦函数的阵型风或者呈阶梯状的渐变风,转换为电能的效率为0.3≤η2≤0.4,风能转换为电能的最大功率为0.5 MW.
进行强化学习过程中,学习步长α取值为1,折扣因子λ取值为0.85,设定的迭代次数上限为20×104次.
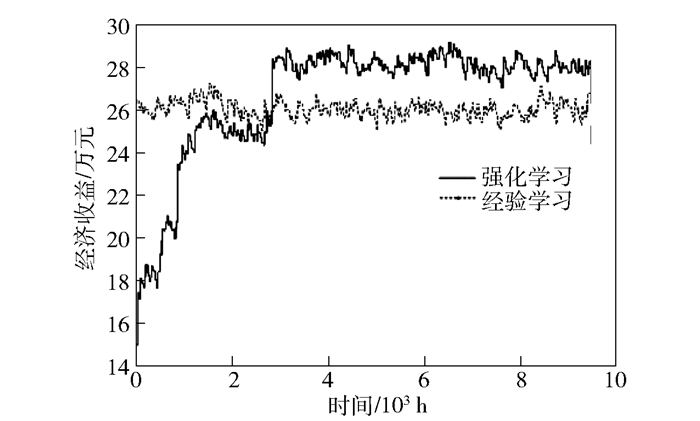
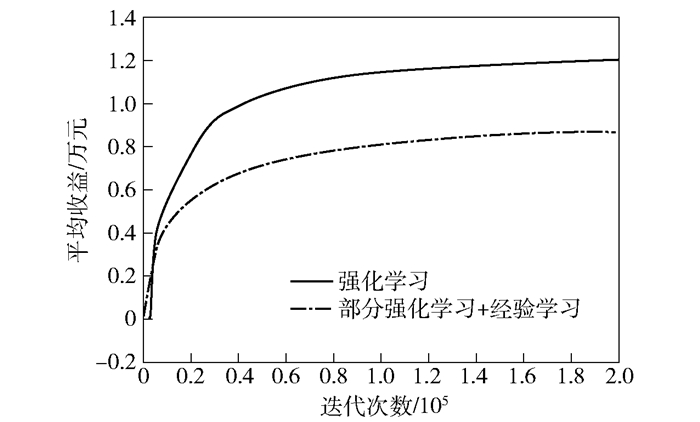
总收益增长趋势如图 4所示,在开始时收益处于较低水平,但通过Q算法的不停迭代,不断逼近最优解,系统迭代到仿真中的3 000 h时就会趋向于收敛,这时的总收益将会达到一个相对最大值并超过经验学习的效益(经验学习是基于马尔可夫决策过程的算法,其核心是按照当前利益最大化这个设定做状态转移).每小时的平均收益增长趋势如图 5所示,在迭代了2×105次后也趋向于收敛,与部分强化学习策略(有一部分采用强化学习优化,另一部分采用经验策略)相比较,在开始的迭代阶段,部分强化学习策略是采用当前利益最大化的策略,所以在刚开始增长较快,收益较高,但由于缺乏对于未来策略的预测,所以在后期增长较为缓慢;强化学习虽然在一开始收益较低,是因为其仍在探索试错的阶段,但在后期能够稳定地增长,说明其通过探索有了一些经验,具备了一定的调度能力.
|
图 4 经济总收益增长趋势 |
|
图 5 平均经济收益增长趋势 |
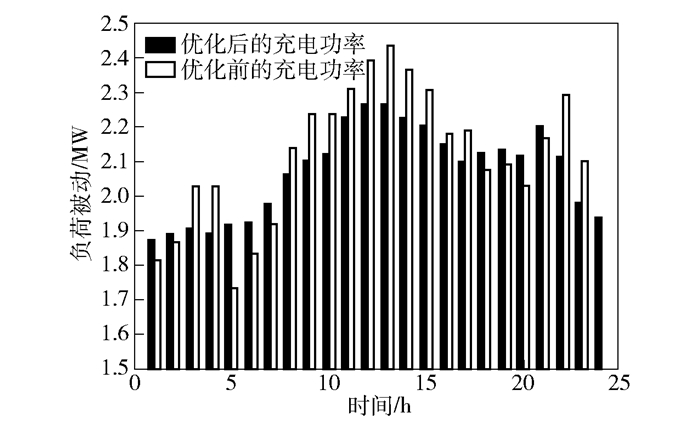
一天24 h的充电功率如图 6所示,可以看出白天的充电功率较高,夜晚较低,是因为白天用户用电量较大;优化后的充电功率明显比优化前的充电功率更加稳定,在白天功率较大的时间段,优化后的系统通过储能系统的功率调节使得整个功率降低,在夜晚功率较低的时间段,优化后的系统充电功率也有所升高.
|
图 6 充电功率对比 |
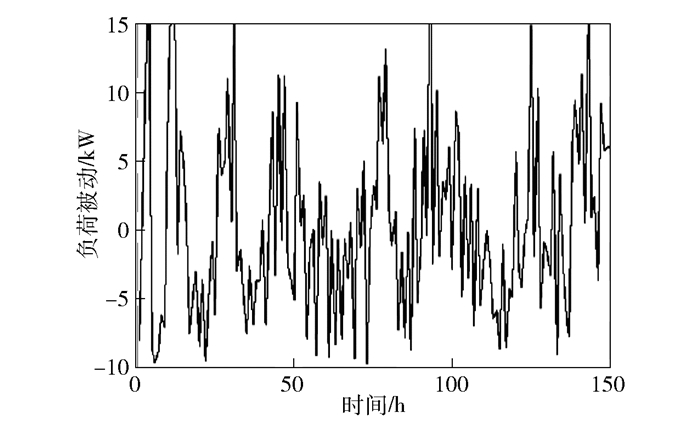
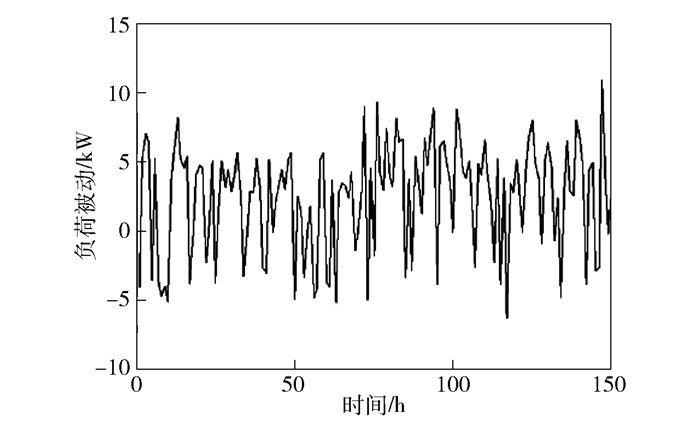
微电网的优化前总负荷如图 7所示,可以看出,未使用电动汽车模型的微电网负荷较高而且不是很稳定.使用了电动汽车对微电网进行削峰填谷后的负荷如图 8所示,可见负荷达到上限的次数明显减少,提高了系统的稳定性,减少了波动.因此,微电网与电动汽车交互后能够明显改善电网的负荷问题.
|
图 7 优化前负荷波动 |
|
图 8 优化后负荷波动 |
每小时的平均碳排放量如图 9所示,可以看出,一开始碳排放量较大,对环境会造成消极的影响,采用了强化学习的不停迭代优化策略后,碳排放量呈现下降趋势并最终达到收敛,证明强化学习对于碳排放优化这一指标也同样适用,对于环境保护具有积极的作用.

|
图 9 碳排放量趋势 |
在仿真中使用了Q学习后,模型能够不停地进行在线学习,最终得到最优的调度策略,使微电网的利益最大化.在应对风能、光伏能的不确定性时,通过调整储能系统的功率,使微电网总的充电功率保持稳定,并且3种方式充电相互协调,紧密耦合,相互影响.同时,将电动汽车系统引入微电网中,能够对微电网负荷进行削峰填谷,使得微电网的总负荷相对稳定,延长了系统设备的使用寿命.在响应环境保护上,采用强化学习的优化策略使碳排放量降低并达到收敛,这对于保护环境具有积极作用和现实意义.
| [1] |
郑漳华, 艾芊. 微电网的研究现状及在我国的应用前景[J]. 电网技术, 2008, 32(16): 27-31. Zheng Zhanghua, Ai Qian. Research status and application prospect of micro power grid in China[J]. Power Grid Technology, 2008, 32(16): 27-31. |
| [2] |
王成山, 李鹏. 分布式发电、微网与智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 34(2): 10-14. Wang Chengshan, Li Peng. Development and challenges of distributed generation, micro grid and intelligent distribution network[J]. Power System Automation, 2010, 34(2): 10-14. |
| [3] |
鞠平, 周孝信, 陈维江, 等. "智能电网+"研究综述[J]. 电力自动化设备, 2018, 38(5): 2-11. Ju Ping, Zhou Xiaoxin, Chen Weijiang, et al. Research review of "smart grid +"[J]. Electric Power Automation Equipment, 2018, 38(5): 2-11. |
| [4] |
张素香. 智能小区的商业智能[J]. 北京邮电大学学报, 2012, 35(5): 94-97. Zhang Suxiang. Business intelligence of intelligent community[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(5): 94-97. |
| [5] |
Thomas Strasser, Filip Andrén, Johannes Kathan, et al. A review of architectures and concepts for intelligence in future electric energy systems[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2424-2438. DOI:10.1109/TIE.2014.2361486 |
| [6] |
Roberts B. Capturing grid power[J]. IEEE Power and Energy Magazine, 2009, 7(4): 32-41. DOI:10.1109/MPE.2009.932876 |
| [7] |
徐丰.微电网建模及其控制策略研究[D].南京: 南京理工大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10288-1013354506.htm
|
| [8] |
周围, 韩礼冬, 李钢, 等. 基于PSCAD/EMTDC的微电网永磁直驱风力发电系统建模与仿真研究[J]. 电气技术, 2016, 17(2): 52-57. Zhou Wei, Han Lidong, Li Gang, et al. Modeling and simulation of PSCAD/EMTDC based micro grid permanent magnet direct drive wind power generation system[J]. Electrical Technology, 2016, 17(2): 52-57. |
| [9] |
刘国静, 韩学山, 王尚, 等. 基于强化学习方法的风储合作决策[J]. 电网技术, 2016, 40(9): 2729-2736. Liu Guojing, Han Xueshan, Wang Shang, et al. Wind storage cooperative decision-making based on reinforcement learning[J]. Power Grid Technology, 2016, 40(9): 2729-2736. |
| [10] |
钟伟锋.智能电网中V2G系统能量管理及应用研究[D].广东: 广东工业大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-11845-1016156947.htm
|
| [11] |
周文辉, 钟伟锋, 吴杰, 等. 面向智能电网负荷调节的自适应储能系统控制[J]. 北京邮电大学学报, 2017, 40(1): 32-35. Zhou Wenhui, Zhong Weifeng, Wu Jie, et al. Adaptive energy storage system control for smart grid load regulation[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(1): 32-35. |
| [12] |
Wei C, Zhang Z, Qiao W, et al. An adaptive network-based reinforcement learning method for MPPT control of PMSG wind energy conversion systems[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7837-7848. DOI:10.1109/TPEL.2016.2514370 |
| [13] |
Etemad S, Mozayani N. Using reinforcement learning to make smart energy storage sources in microgrid[C]//2015 30th International Power System Conference (PSC). Tehran: [s. n.], 2015: 345-350.
|
| [14] |
Wu Jingda, He Hongwen, Peng Jiankun, et al. Continuous reinforcement Jingda learning of energy management with deep Q network for a power split hybrid electric bus[J]. Applied Energy, 2018, 222(15): 799-811. |


