2. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 西安 710071
针对NLOS测距存在误差的问题,提出一种基于信道模糊关联识别的NLOS测距误差补偿算法.根据先验信道特征参数分布信息构造信道特征参数模糊隶属矩阵,并利用灰色关联分析方法计算归一化权值矩阵,进而获得模糊综合评价矩阵来对信道环境进行识别.在此基础上,根据信道识别结果构建Huber代价函数,通过Huber线性回归方法对原始测距结果进行迭代重构,将重构结果作为Kalman滤波的测量值进行滤波.仿真结果表明,所提算法可以有效提高NLOS环境下的测距精度,在信噪比大于-2 dB时可以达到厘米级测距精度.
2. State Key Laboratory of Integrated Service Networks, Xidian University, Xi'an 710071, China
Aiming at the problem of ranging errors in non line of sight (NLOS) ranging, an NLOS ranging error compensation algorithm is proposed based on fuzzy association channel identification. The algorithm constructs fuzzy membership matrix of channel feature parameters based on the prior channel feature parameter distribution information, and uses gray correlation analysis method to calculate the normalized weight matrix, so that to obtain the fuzzy comprehensive evaluation matrix to identify the channel environment. On this basis, the Huber residual cost function is constructed according to the channel identification result, and the original ranging result is iteratively reconstructed by Huber linear regression method, which is filtered as the measured value of Kalman filter. Simulation show that the proposed algorithm can improve the ranging accuracy under NLOS effectively, and the range accuracy of this algorithm can reach centimeter level when signal-to-noise ratio is -2 dB.
新一代导航定位系统的升级对高精度测距技术提出了更高的要求.在视距(LOS, line of sight)信道环境下,基于正交频分复用(OFDM, orthogonal frequency division multiplexing)时频特性的到达时间(TOA, time of arrival)估计方法在一定程度上可以提高测距精度[1],但在非视距(NLOS,non line of sight)信道环境下,高精度测距技术仍面临巨大的挑战,因此NLOS信道下的测距误差补偿已成为高精度测距技术的一个研究热点.而进行NLOS测距误差补偿面临2个关键问题:一是识别信道环境,二是根据信道识别结果对测距误差进行补偿[2].
信道识别即利用LOS信道和NLOS信道不同的传播特征,包括莱斯系数、偏度、峭度等,来鉴别信号传播环境[3]. Xiao等[4]利用机器学习理论对接收信号特征进行分析,利用先验信息训练特征检测门限来识别信道. Li等[5]通过提取信号特征进行最优特征参数组合并检测信道,相对于使用固定参数的检测方法,进一步提高了信道识别的准确性. Chitambira等[6]利用最小二乘向量机在准确识别信道的同时对NLOS误差进行补偿.虽然学习类算法可以提高信道识别精度,但算法的高复杂度限制了其可移植性,使用训练门限进行直接识别也容易引起识别误差.
利用信道识别结果抛弃NLOS测距异常结果可以在一定程度上提高测距精度[7],但是在复杂环境下NLOS误差的构成很复杂,直接进行处理是不现实的. Xiao和Li等[4-5]利用接收信号强度对测距结果进行重构,测距精度有限且不适用于室外复杂场景. Zhang等[8]提出利用Wylie算法,对多组测距结果进行拟合并偏移,从而重构NLOS测距结果. Hu等[9]提出利用拓展Kalman滤波器对测距结果进行迭代滤波,可以补偿NLOS测距误差,但是由于偏差较大的NLOS误差存在,误差补偿精度有限.
针对NLOS测距误差识别与补偿精度有限的问题,笔者提出一种基于信道模糊关联识别的NLOS测距误差补偿算法.通过联合多个信道特征参数,构造模糊隶属矩阵,并利用灰色关联分析方法获得模糊评价的权值矩阵,计算信道特征参数与测距结果之间的灰色关联系数并做归一化处理,使用模糊综合评价方法对信道进行判决.另外,考虑到NLOS测距误差的存在,结合信道识别结果,利用Huber线性回归,将NLOS测距异常值进行重构,并将重构后的结果作为Kalman滤波测量值进一步处理.通过仿真结果验证了所提算法在信噪比大于-2 dB时测距误差可达厘米级,说明所提算法具有较高的NLOS测距误差补偿精度的作用.
相较于之前的误差补偿算法,所提算法的主要贡献如下:
1) 通过测距结果联合信道多参数进行灰色关联分析,利用模糊综合评价方法对信道进行判别,解决了传统算法鲁棒性不足的问题,提升LOS及NLOS信道识别准确率.
2) 利用Huber代价函数兼顾均方误差和均方绝对值误差特性,有效地处理偏差极值并对误差进行重构,从而解决了传统均方误差代价函数对偏差极值敏感的问题,降低了测距误差,提升了测距精度.
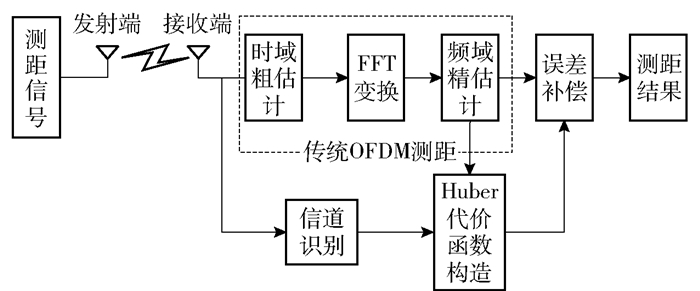
1 系统模型OFDM测距模型如图 1所示.在时域上,根据收发测距信号最大相关原理进行时域粗估计,在频域上,利用OFDM频率偏移实现信号传播时延精估计,从而获得第k组原始测距结果为
| $ {d_k} = c{T_{\rm{s}}}\left\{ {{\rm{arg}}\left( {\mathop {{\rm{max}}}\limits_m \left| {\sum\limits_{n = 0}^{N - 1} {({y_n}x_{n + m}^*)} } \right|} \right) + \frac{{\hat \varphi }}{{2\pi }}} \right\} $ | (1) |
|
图 1 高精度测距系统组成 |
其中:dk为第k组测距结果,c为光速,Ts为信号采样间隔,yn为第n个OFDM采样接收信号,xn为第n个OFDM采样发射信号,N为接收信号的采样点数,*表示取共轭,
先对信道进行识别,并根据信道识别结果与原始测距结果构造Huber代价函数.通过Huber代价函数对原始测距结果进行重构以减小测距误差,得到最终测距结果.
在NLOS信道下进行M组测距,则均方测距误差可以表示为
| $ E = \frac{1}{{2M}}\sum\limits_{k = 1}^M {{{({d_k} - d)}^2}} $ | (2) |
其中d为真实距离.假设其中有K组LOS测距结果,M-K组NLOS测距结果,则式(2)可以改写为
| $ E = \frac{1}{{2M}}\left( {\sum\limits_{k = 1}^K {{{({d_{ {\rm{los}} ,k}} - d)}^2}} + \sum\limits_{i = 1}^{M - K} {{{({d_{{\rm{nlos}},i}} - d)}^2}} } \right) $ | (3) |
其中:dlos, k和dnlos, i分别为第k组LOS测距结果和第i组NLOS测距结果.
2 NLOS测距误差补偿算法 2.1 误差分析如式(3)所示,测距误差分为LOS测距误差和NLOS测距误差,令elos和enlos分别表示LOS测距误差和NLOS测距误差.在LOS信道下进行测距,由于受高斯白噪声的影响,测距结果会出现均值为0,服从正态分布的偏差,则LOS测距误差范围为
| $ - \alpha \le {e_{{\rm{ los }}}} \le \alpha $ | (4) |
其中α为LOS测距误差上界.而在NLOS信道下进行测距时,信号存在一定的遮挡,会在LOS测距误差的基础上附加一个正向的测距偏差,则NLOS测距误差范围为
| $ 0 \le {e_{{\rm{ nlos }}}} \le \beta $ | (5) |
其中β为NLOS测距误差上界.为了最小化测距误差,需要最小化测距误差上界:
| $ {\rm{min}}{\kern 1pt} {\kern 1pt} E = {\rm{min}}({e_{{\rm{ los }}}} + \delta {e_{{\rm{nlos}}}}) = {\rm{min}}(\alpha + \delta \beta ) $ | (6) |
其中:δ为表征信道状态的参数,LOS信道下,δ = 0;NLOS信道下,δ = 1.
综上,LOS信道下测距结果只包含正态LOS测距误差,NLOS信道下2种测距误差同时存在.为了最小化测距误差,应该针对不同信道场景设计不同的误差补偿算法,因此需要对测距环境进行信道识别.传统算法使用单一参数进行信道识别准确度有限,且鲁棒性不足.因此,笔者采用基于多参数联合的信道识别方法提高信道识别准确率.
对LOS信道和NLOS信道2种状态的识别是一个二元检测问题,即最小化二元检测误差概率:
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{min}}(p({H_0}|{H_1}) + p({H_1}|{H_0})) = }\\ {{\rm{min}}\{ p({H_0}|{u_{{\rm{ los }}}} > {u_{{\rm{ nlos }}}}) + p({H_1}|{u_{{\rm{ los }}}} < {u_{{\rm{ nlos }}}})\} } \end{array} $ | (7) |
其中:H0表示LOS信道,H1表示NLOS信道,ulos和unlos分别为信道特征参数集合与LOS信道以及NLOS信道的先验信道特征参数集合之间的距离.由于信道特征参数量纲不同,ulos和unlos不能直接使用空间几何距离计算,需要引入加权系数:
| $ \left. {\begin{array}{*{20}{l}} {{u_{{\rm{los}}}} = {w_1}{b_{{\rm{l,1}}}} + {w_2}{b_{{\rm{l,2}}}} + \cdots + {w_m}{b_{1,m}}}\\ {{u_{{\rm{nlos}}}} = {w_1}{b_{{\rm{n,1}}}} + {w_2}{b_{{\rm{n,2}}}} + \cdots + {w_m}{b_{{\rm{n}},m}}} \end{array}} \right\} $ | (8) |
其中:wm为第m个信道特征参数的加权系数,bl, m和bn, m分别为第m个信道特征参数与相应的LOS信道和NLOS信道的先验信道特征参数之间的距离.但是由于先验信道特征参数不是一个固定值,而是一个分布区间,式(8)无法直接计算.在模糊理论中,模糊隶属度可以表征参数对区间的距离大小,模糊隶属度越大,则参数对区间的距离越小,则式(8)可以转化为
| $ \begin{array}{*{20}{c}} {{\rm{min}}(p({H_0}|{H_1}) + p({H_1}|{H_0})) = }\\ {{\rm{min}}\{ p({H_0}|\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{R}}_1} < \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{R}}_{\rm{n}}}) + p({H_1}|\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{R}}_1} > \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{R}}_{\rm{n}}})\} } \end{array} $ | (9) |
其中:W为加权矩阵,Rl和Rn分别为LOS信道和NLOS信道的模糊隶属度向量.信道特征参数的模糊隶属矩阵R = [Rl Rn],通过利用模糊综合评价方法可得模糊综合评价矩阵:
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{WR}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}&{{a_{\rm{n}}}} \end{array}} \right] $ | (10) |
对信道进行识别,仅需比较al和an的大小.若al大于an,则信道为LOS信道,反之,信道为NLOS信道.为了获得模糊综合评价矩阵A,需要分别计算模糊隶属矩阵R和相应的加权矩阵W.
根据先验信息,相对于LOS信道,NLOS信道下冲激响应幅度更趋近于正态分布,因此,NLOS信道冲激响幅度的峭度、偏度、莱斯系数和K-S系数均小于LOS信道下相应的参数,选择其作为信道特征参数.用Q = {q1, q2, q3, q4}表示信道特征参数集合,V = {v1, v2}表示信道状态集合,包括LOS信道v1和NLOS信道v2,则信道特征参数与信道状态之间的模糊关系可以表示为
| $ f({q_i})\mathop = \limits^{Q \to V} ({r_{1,i}},{r_{{\rm{n}},i}}) $ | (11) |
其中:f为信道特征参数和信道状态之间的模糊映射函数,rl, i和rn, i分别为第i个信道特征参数对LOS信道和NLOS信道的模糊隶属度系数,i = 1, 2, 3, 4时信道特征参数分别为峭度、偏度、莱斯系数和K-S系数.则所有信道特征参数的模糊隶属矩阵为
| $ \mathit{\boldsymbol{R}} = {\left[ {\begin{array}{*{20}{c}} {{r_{{\rm{l,1}}}}}&{{r_{{\rm{l,2}}}}}&{{r_{{\rm{l,3}}}}}&{{r_{{\rm{l,4}}}}}\\ {{r_{{\rm{n,1}}}}}&{{r_{{\rm{n,2}}}}}&{{r_{{\rm{n,3}}}}}&{{r_{{\rm{n,3}}}}} \end{array}} \right]^{\rm{T}}} $ | (12) |
在似然比检验方法中,峭度、偏度、莱斯系数和K-S系数的检验门限分别表示为k1、k2、k3和k4,根据Li等[5]计算的实际信道特征参数分别为m1、m2、m3和m4.设信道特征参数大小等于检测门限时,其对于LOS信道和NLOS信道的隶属度系数都是ω.信道特征参数越大,信道属于NLOS信道的概率越小.反之,信道特征参数越小,信道属于NLOS信道的概率越大.因此,可以构造信道特征参数对NLOS信道的模糊隶属度系数为
| $ {r_{{\rm{n}},i}} = \left\{ {\begin{array}{*{20}{l}} {0,\quad \theta < - \omega }\\ {\omega + \theta ,\quad |\theta | \le \omega }\\ {1,\quad \theta > \omega } \end{array}} \right. $ | (13) |
其中:θ = mi/ki-1表示实际信道特征参数与检测门限之间的模糊距离关系,i = 1, 2, 3, 4.因为信道只包含LOS信道和NLOS信道2种环境,所以信道特征参数对LOS信道下的模糊隶属度系数可以定义为rl, i = 1-rn, i,i = 1, 2, 3, 4.
为了计算加权矩阵W,需要确定每个参数和信道之间的相关程度.信道状态与信道特征参数之间的关系是灰色的,可以利用灰色关联理论分析其关联关系.考虑到信道状态是一个逻辑值,因此,笔者使用测距结果代替信道状态值进行灰色关联分析,将归一化的灰色关联系数作为信道状态模糊综合评价的加权系数.
为了便于分析,将测距结果和峭度、偏度、莱斯系数、K-S系数五组数据集合分别标记为s0,s1,s2,s3和s4.根据灰色关联理论,第n次测距sm对s0的关联系数可以定义为
| $ {\xi _m}(n) = \frac{{{\varDelta _{{\rm{min}}}} + g{\varDelta _{{\rm{max}}}}}}{{{\varDelta _{im}}(n) + g{\varDelta _{{\rm{max}}}}}} $ | (14) |
其中:n = 1, 2, 3, …, M,M为测距次数,g为介于[0, 1]区间上的灰色系数,Δim(n) = |si(n)-sm(n)|为第n次测距中的si和sm之间差的绝对值,Δmin为Δim(n)的最小值,Δmax为Δim(n)的最大值.
为了方便信道状态模糊综合评价,需要对灰色关联系数进行归一化:
| $ {w_m} = \frac{{\sum\limits_{n = 1}^M {{\xi _m}} (n)}}{{\sum\limits_{m = 1}^4 {\sum\limits_{n = 1}^M {{\xi _m}} } (n)}} $ | (15) |
其中:m = 1, 2, 3, 4.则由wm构成的W即为信道特征参数的加权矩阵,联合信道特征参数矩阵模糊隶属矩阵R通过式(10)获得信道模糊综合评价矩阵A进行信道识别.
根据信道识别结果,构建Huber代价函数并利用Huber线性回归方法对测距结果进行重构,可以在补偿NLOS测距误差的同时,最小化LOS测距均方误差,提高测距精度.
2.2 Huber-Kalman滤波误差补偿算法根据模型分析,NLOS信道环境下LOS和NLOS测距误差可能同时存在,为了最小化测距误差,利用Huber线性回归方法对传统OFDM的原始测距结果进行重构,并将重构后的结果进行Kalman滤波,从而提高测距精度,增强系统的鲁棒性.对式(1)中的原始测距结果进行回归分析,假设回归方程表达式为
| $ {d_k} \simeq \mathit{\boldsymbol{G}}{\hat \chi _k} + \mathit{\boldsymbol{L}}({\chi _k} - {\hat \chi _k}) $ | (16) |
其中:G为量测矩阵,L为斜率矩阵,χk和
| $ \left[ {\begin{array}{*{20}{c}} {{d_k} - \mathit{\boldsymbol{G}}{{\hat \chi }_k} + \mathit{\boldsymbol{L}}{{\hat \chi }_k}}\\ {{{\hat \chi }_k}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}}{\chi _k} + {\eta _k}}\\ {{\chi _k} - {\varepsilon _k}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{L}}\\ \mathit{\boldsymbol{I}} \end{array}} \right]{\chi _k} + \left[ {\begin{array}{*{20}{c}} {{\eta _k}}\\ { - {\varepsilon _k}} \end{array}} \right] $ | (17) |
其中:ηk为拟合误差,εk为预测误差,I为单位阵.为了便于分析,将式(17)改写为
| $ {\mathit{\boldsymbol{z}}_k} = {\mathit{\boldsymbol{M}}_k}{\chi _k} + {\mathit{\boldsymbol{\zeta }}_k} $ | (18) |
其中:
| $ v = {\mathit{\boldsymbol{M}}_k}{\chi _k} - {\mathit{\boldsymbol{z}}_k} $ | (19) |
在NLOS测距信道下存在LOS和NLOS两种测距误差,对测距误差进行补偿,需要最小化回归残差:
| $ {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \rho (v) = {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rho _1}(v) + {\rho _n}(v)) $ | (20) |
其中:ρ(υ)为测距残差代价函数,ρl(υ)和ρn(υ)分别为LOS和NLOS测距结果的残差代价函数. LOS信道时,ρn(υ)不存在,因此可以使用最小二乘方法构造均方误差代价函数ρ(υ) = ρl(υ) = υ2/2;NLOS信道时,存在测距偏差极值,均方误差代价函数对偏差极值比较敏感,需要引入调节因子来构造残差代价函数.根据Wang等[10]的研究结果,由于Huber代价函数兼顾均方误差和均方绝对值误差特性,可以有效处理偏差极值,因此定义Huber残差代价函数ρ(υ)为
| $ \rho (v) = \left\{ \begin{array}{l} \frac{1}{2}{v^2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} |v| < \gamma \\ \gamma |v| - \frac{1}{2}{\gamma ^2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} |v| \ge \gamma \end{array} \right. $ | (21) |
其中:γ为阈值因子,与测距信道有关.信道越接近LOS信道,γ取值越大,Huber代价函数退化为最小二乘均方误差.相反,当信道越接近于NLOS信道,γ取值越小.阈值因子需要保证LOS测距回归残差均小于γ,而NLOS测距回归残差大于γ,有
| $ \left. {\begin{array}{*{20}{l}} {\gamma > {\rm{max}}|{v_{{\rm{ los }}}}|, {\rm{LOS}} }\\ {\gamma \le {\rm{min}}|{v_{{\rm{ nlos }}}}|, {\rm{NLOS}} } \end{array}} \right\} $ | (22) |
其中υlos和υnlos分别为LOS和NLOS测距回归残差.如式(22)所示,利用信道模糊综合评价矩阵A进行信道识别,并根据信道识别结果设置阈值调节因子.
对于最小化残差代价函数,可以定义偏导数φ(υ) = ∂ρ(υ)/∂υ,当代价函数最小时,偏导数为0,即
| $ \sum\limits_{i = 1}^N \varphi (v)\frac{{\partial v}}{{\partial {\chi _k}}} = 0 $ | (23) |
其中:k = 1, 2, …, M,M为测距次数.
定义函数ψ(υ) = φ(υ)/υ,对角矩阵Ψ = diag[ψ(υ)], 则有
| $ \sum\limits_{i = 1}^N \varphi (v)\frac{{\partial v}}{{\partial {\chi _k}}} = \mathit{\boldsymbol{M}}_k^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}({\mathit{\boldsymbol{M}}_k}{\chi _k} - {\mathit{\boldsymbol{z}}_k}) = 0 $ | (24) |
根据Huber线性回归方法重构的测距状态值为
| $ {\tilde \chi _k} = {(\mathit{\boldsymbol{M}}_k^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{M}}_k})^{ - 1}}\mathit{\boldsymbol{M}}_k^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{z}}_k} $ | (25) |
补偿后的测距结果只受高斯白噪声影响,因此可以进一步利用Kalman滤波方法对Huber重构补偿后的测距结果进行平滑滤波,以消除随机测距误差,提高测距精度.
3 性能仿真与分析考虑到测距系统中多径信号以簇的形式出现,且呈现NLOS多径信道的特点,在信道识别和NLOS测距误差抑制仿真验证中利用Saleh-Valenzuela (SV)信道随机幅度时延等特点,并结合第5代移动通信系统中的定位仿真场景对NLOS信道模型进行配置,其信道配置参数见表 1.
|
|
表 1 信道参数配置 |
基于表 1的信道参数配置,对所提算法的NLOS信道识别概率和测距误差进行了仿真与分析.
3.1 NLOS信道识别仿真分析首先验证了NLOS信道下所提出的基于模糊关联的信道识别方法的识别准确率.仿真中,OFDM系统中子载波的数量和间隔分别为1 024 kHz和15 kHz.仿真结果如图 2所示.

|
图 2 不同SNR时NLOS信道识别准确度 |
通过图 2可以看出,基于偏度和K-S系数检测方法的识别准确率相对于基于峭度和莱斯系数检测方法的识别准确率稍高一些,这主要因为基于偏度和K-S系数检测方法是基于数据的正态性,特征明显.而峭度和莱斯系数2个参数在LOS信道和NLOS信道下界限不是特别明显,因此,识别准确率更低一些.对比2个信噪比下的NLOS信道识别准确率可以发现,NLOS信道识别准确率和信噪比大小有关,且信噪比越高,识别准确率越高,在2种信噪比下,所提算法相对于单参数似然比检验识别方法,识别准确率都有一定的提高.
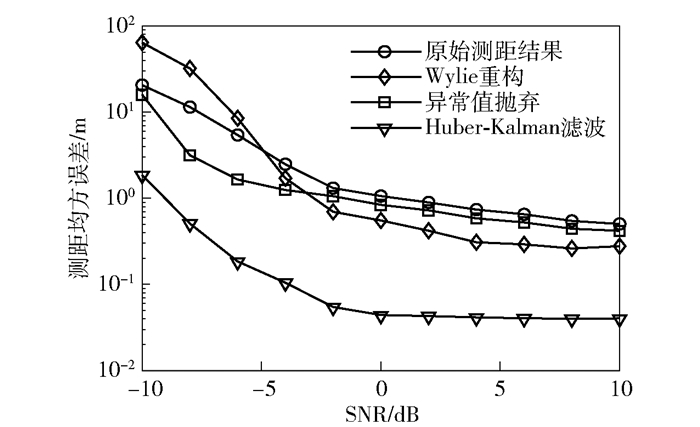
3.2 测距误差仿真分析为了进一步给出所提Huber-Kalman滤波误差补偿算法与其他算法的测距精度,图 3和图 4分别给出了不同算法测距误差随信噪比改变的变化趋势以及不同信噪比下的测距误差累积分布函数(CDF, cumulative distribution function)曲线.
|
图 3 测距误差随SNR改变的变化趋势 |
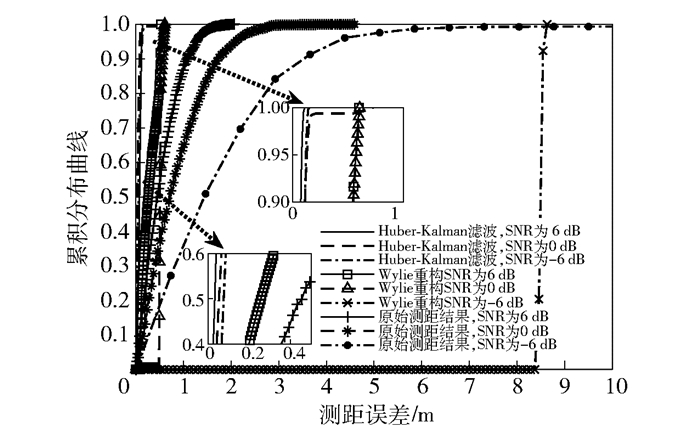
|
图 4 不同信噪比下测距误差的CDF曲线 |
从图 3可以看出,所提出的Huber-Kalman滤波算法的定位精度高于异常值抛弃和Wylie重构算法,这是由于Huber线性回归方法通过线性回归有效补偿NLOS测距误差,而不影响LOS测距结果,因此可以有效提高测距精度.
从图 4可以看出,所提Huber-Kalman滤波算法大大减小了测距误差,且最大误差上限相比于显著降低,使得重构后的测距误差比较集中于一个稳定的误差值.这是因为经过Huber重构及Kalman平滑滤波,消除了NLOS信道所产生的偏差极值和高斯白噪声所产生的随机误差.
从图 3和图 4可见,Huber-Kalman滤波算法可以有效补偿NLOS测距误差,降低测距误差上限,提高测距精度,在-4 dB和-6 dB时的测距误差为分米级,在信噪比大于-2 dB时的测距误差可达厘米级.
3.3 算法计算复杂度分析Wylie算法需要经过结果拟合预测、拟合误差计算及Wylie误差重构等步骤进行测距误差重构,假设测距系统进行N次测距,结果拟合预测过程的计算复杂度为O(N2),拟合误差计算的计算复杂度为O(N),Wylie误差重构的计算复杂度为O(N),因此Wylie算法的计算复杂度为O(N2)+O(N).
所提NLOS误差补偿算法主要分为结果线性拟合、模糊综合评判、信道灰色关联分析及Huber误差重构几个步骤.结果线性拟合的计算复杂度为O(N);结合灰色关联的信道模糊综合评判的计算复杂度为O(N);Huber重构计算复杂度为O(N3),因此所提算法的计算复杂度为O(N3)+O(N).
与现有算法相比,所提算法复杂度略高于Wylie误差重构算法,但复杂度提高不明显.同时由于所提算法能够大大提高精度测距精度,所以在高精度测距领域具有较大的应用价值.
4 结束语提出了一种基于信道模糊关联识别的NLOS误差补偿算法.首先根据先验信道特征参数分布信息估计LOS信道和NLOS信道的模糊隶属度系数,同时结合灰色关联分析方法构建归一化的信道识别权值矩阵,最终生成模糊综合评价矩阵对信道环境进行识别.在此基础上,利用Huber线性回归方法对原始测距结果进行重构,并将重构结果作为测量值进行Kalman滤波.仿真结果表明, 所提算法可以准确识别信道环境,并有效减小NLOS误差极值分布,相对于现有算法可以有效提高NLOS测距误差补偿精度.
| [1] |
Siddig A, Bleakley C J, Makki A, et al. High-resolution time of arrival estimation for OFDM-based transceivers[J]. Electronics Letters, 2015, 51(3): 294-296. |
| [2] |
Pak J M, Ahn C K, Shi Peng, et al. Distributed hybrid particle FIR filtering for mitigating NLOS effects in TOA-based localization using wireless sensor networks[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 5182-5191. DOI:10.1109/TIE.2016.2608897 |
| [3] |
Silva B, Hancke G P. IR-UWB-based non-line-of-sight identification in harsh environments:principles and challenges[J]. IEEE Transactions on Industrial Informatics, 2016, 12(3): 1188-1195. DOI:10.1109/TII.2016.2554522 |
| [4] |
Xiao Zhuoling, Wen Hongkai, Markham A, et al. Non-line-of-sight identification and mitigation using received signal strength[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1689-1702. DOI:10.1109/TWC.2014.2372341 |
| [5] |
Li Xiaohui, Cai Xiong, Hei Yongqiang, et al. NLOS identification and mitigation based on channel state information for indoor WiFi localization[J]. IET Communications, 2017, 11(4): 531-537. DOI:10.1049/iet-com.2016.0562 |
| [6] |
Chitambira B, Armour S, Wales S, et al. NLOS identification and mitigation for geolocation using least-squares support vector machines[C]//2017 IEEE Wireless Communications and Networking Conference(WCNC). New York: IEEE Press, 2017: 1-6.
|
| [7] |
Yan Jun, Wu Lenan. A data fusion scheme for modified EKF banks positioning algorithm in mixed LOS/NLOS conditions[C]//12th IEEE International Conference on Ubiquitous Intelligence and Computing and 15th IEEE International Conference on Autonomic and Trusted Computing and 15th IEEE International Conference on Scalable Computing and Communications and Its Associated Workshops(UIC-ATC-ScalCom). New York: IEEE Press, 2015: 1249-1252.
|
| [8] |
Zhang Lan, Chen Feng, Yu Yao. Research on hybrid location algorithm with high accuracy in indoor environment[C]//34th Chinese Control Conference. New York: IEEE Press, 2015: 15454267.
|
| [9] |
Hu Nan, Wu Chengdong, Li Chen, et al. The NLOS localization algorithm based on the linear regression model of extended Kalman filter[J]. Journal of Image and Graphics, 2016, 4(2): 141-144. DOI:10.18178/joig.4.2.141-144 |
| [10] |
Wang Hongwei, Li Hongbin, Zhang Wei, et al. A unified framework for M-estimation based robust Kalman smoothing[J]. Signal Processing, 2019, 158: 61-65. DOI:10.1016/j.sigpro.2018.12.017 |


