2. 东北大学 计算机科学与工程学院, 沈阳 110169;
3. 东软医疗系统股份有限公司, 沈阳 110167
准确评估路网脆弱性是道路规划的基础.为兼顾路段和交叉口拥堵的影响,引入瓶颈线路的概念,旨在识别因道路容量较小而难以抵御突发事件的通行线路.在此基础上,提出了基于谱分析的路网脆弱性分析方法,利用图谱分区中的最小分割理论定位瓶颈线路.为解决瓶颈线路拥堵所致的大面积切断式分割问题,采取了基于连通贡献量的路网完善措施,在新建和扩建等方面对路网保护措施提出改进建议.仿真结果表明,与其他方案相比,所提出的脆弱性识别机制对路网中的瓶颈线路定位更准确,且可避免产生路网切断式分割现象.
2. School of Computer Science and Engineering, Northeastern University, Shenyang 110169, China;
3. Neusoft Medical Systems Company Limited, Shenyang 110167, China
Accurately assessing the vulnerability of road networks is the basis of road planning. The congestion effects of road sections and intersections are considered. The concept of bottleneck lines is introduced to identify the vulnerable line, it is difficult to withstand emergencies due to small road capacity. A road network vulnerability analysis method based on spectral analysis is proposed thereafter, using the minimum segmentation theory of the spectral partitioning to locate the bottleneck line. In addition, in order to solve the problem of large-area cut-off segmentation, a road network improvement measure based on connectivity contribution is proposed, providing improvement suggestions for road network protection. Simulations show that the proposed method is more accurate in locating the bottleneck line compared to comparison scheme, and the network improvement measure can effectively avoid the segmentation phenomenon of the road network.
近年来,交通事故、假日车流量激增等交通问题造成城市交通严重堵塞甚至瘫痪,特别是道路交通网络(以下简称路网)中某些关键单元失效或拥堵可能会引发整个路网的大面积阻断,甚至导致全网崩溃[1].这些交通拥堵问题因其后果严重而引起众多学者的广泛关注,从而引发了对路网脆弱性的研究.
路网脆弱性分析有助于城市道路规划人员根据路网当前运行状态进行灾前减灾管理,提前识别出易影响整个路网运行状态及效率的通行线路[2]. Mattsson等[3]将路网脆弱性分为系统脆弱性和拓扑脆弱性2种,系统脆弱性分析将路网系统的需求与供应作为分析目标以量化路段失效对社会效益造成的损失.相比之下,拓扑脆弱性分析旨在利用图论知识选定对路网整体性能影响较大的网络单元[4-6].众所周知,系统结构决定其基本功能,因此拓扑脆弱性分析是路网规划的基础,对于路网系统鲁棒性设计至关重要.笔者面向拓扑脆弱性对路网进行脆弱性分析,并为相应的规划设计提供参考.
在拓扑脆弱性分析中,以往关于路网脆弱性的研究旨在识别关键链路或节点,当这些链路或节点被移除时,对路网的可访问性影响最大. Chen等[4]提出一种面向“影响区域”的脆弱性分析方法,以评估路段失效在其所属区域的影响.李彦瑾等[5]从城市路网复杂网络特性入手,利用遍历法逐一量化计算路段的交通流量变化.近几年的路网脆弱性或可靠性研究中主要关注于路网的传输连通性,因为连通性决定着传输是否可达,是路网经济效益的基础保证[7]. Bell等[6]面向路网整体连通性,识别出易对路网造成分割现象的通行路段. Akbarzadeh等[8]考虑路网集群连接的紧密型,其中弱连接的集群间的相连链路为路网中的脆弱链路.然而,以上分析未考虑交叉口失效引起的路网结构脆弱性问题.
综上,现有路网脆弱性分析方法大多将路段与交叉口的脆弱性分开研究,忽略了多个路段与交叉口可能造成的运输功能同时失效情况.此外,瓶颈路线的存在和位置是决定路网运输脆弱性的重要因素,这一路线对路网连通性极为重要,但因总道路容量较小而极易发生拥堵事件,从而加剧路网结构的脆弱程度.基于此,笔者兼顾路段和交叉口的拥堵影响,提出一种基于谱分析的路网脆弱性分析方法(RNVS, road network vulnerability analysis method based on spectral analysis),旨在识别出对网络连通性极为重要但却因道路容量小而难以抵御突发事件的瓶颈路线.此外,针对RNVS方案脆弱性分析结果,提出一种基于连通贡献量的路网完善措施(RNICC, road network improvement measures based on connected contribution),在脆弱元素周围进行最优道路新建,使得在弥补路网脆弱性的同时降低道路新建成本.通过简单例证和真实路网例证验证所提方案的可行性.
1 基础知识 1.1 模型与定义将路网模型抽象为图G = (V, E, w),其中,节点集合V = {v1, v2, …, vn}代表路网中的所有交叉口,n为节点数量,链路集合E = {e1, e2, …, em}代表路网中的所有传输路段,m为路段数量,传输路段与交叉口统称为路网道路单元,w为道路单元容量,代表其可容纳的交通流量,节点容量等于与其相连所有链路的容量平均值.结合抽象图G,引入以下定义.
定义 瓶颈线路(流量瓶颈).单元容量较小的一组路段和交叉口集合,集合中单元的拥堵失效将致使路网出现大面积分割现象.
1.2 图Laplacian矩阵MG为网络图G的n维加权邻接矩阵,MG中的矩阵元素mij为
| $ {m_{ij}} = \left\{ {\begin{array}{*{20}{l}} {w(i,j),\quad {\rm{ 若 }}(i,j) \in E,}\\ {0,\quad {\rm{ 其他 }}} \end{array}} \right. $ | (1) |
其中:w(i, j)为网络图G中的链路权重(路段容量),链路(i, j)∈E,节点i, j∈V.
DG为网络图G的度矩阵,其是一个n维主对角矩阵,对角元素dii为与对应节点相连的所有链路的mij值总和:
| $ {d_{ii}} = \sum\limits_{j \in V} {{m_{ij}}} ,j \in V $ | (2) |
除对角元素外的其他元素为0.
LG为网络图G的n维Laplacian矩阵:
| $ {\mathit{\boldsymbol{L}}_G} = {\mathit{\boldsymbol{D}}_G} - {\mathit{\boldsymbol{M}}_G} $ | (3) |
图Laplacian矩阵是对角矩阵与邻接矩阵之差,因此图Laplacian矩阵的非对角元素是邻接矩阵对应非对角元素的相反数.此外,由于MG为实对称矩阵,故矩阵LG不仅是实对称矩阵,还是半正定矩阵,因此矩阵LG有N个非负实数特征值λ1 = 0≤λ2≤…≤λn.其中,第2小特征值对应的特征向量代表图的代数连通性,可以用来描述图的很多性质[9],且可分析图像切割问题.
2 路网脆弱性识别 2.1 问题描述设计方案的目标是识别出路网中极易发生拥堵的瓶颈线路,并分析瓶颈线路对路网造成分割后的子网相对大小.采用A、B表示瓶颈路段所造成的2个分割子网,通过最小化A、B两个子网道路单元个数差来识别可造成最大效益损害的破坏场景.
路网传输道路最基本的功能特性是连通性,在路网切断式分割现象中,一般利用交叉口数量来衡量切割子网的大小,因此切割后两子网的大小越接近,对网络连通性的破坏程度越高.利用图 1进行说明,链路1和链路2代表路网中2种典型的双向传输道路.显见,若链路2发生拥堵,对路网整体传输连通性影响相对较小;相比之下,若链路1发生拥堵失效,路网将被分割为2个交叉口数量相近的不可互通子网,对网络整体连通性会造成巨大破坏,极大地削弱了路网的传输功能.因此,应识别出对应的瓶颈线路并制定相应的完善措施,从而避免出现这种瓶颈线路的分割情况.
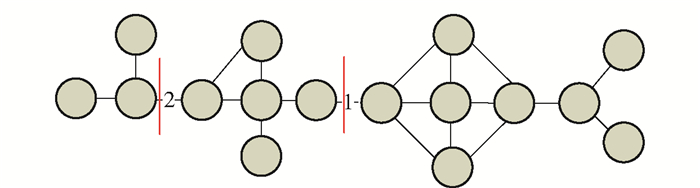
|
图 1 典型路网简化图 |
基于此,设计方案的目标可用以下公式表示:
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{\begin{array}{*{20}{c}} {A,B \subset G}\\ {V(A) = V(B)} \end{array}} {\rm{cut}} (A,B) = {\rm{min}}\frac{{\sum\limits_{i \in A,j \in B} w (i,j)}}{{V(A)V(B)}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{bo}}{{\rm{t}}_{{\rm{road}}}} = \sum\limits_{i \in A,j \in B} {(i,j)} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} V(A) = \sum\limits_{i \in V} {{A_i}} ,{A_i} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} i \in A}\\ {0,}&{{\rm{其他}}} \end{array}} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} V(B) = \sum\limits_{i \in V} {{B_i}} ,{B_i} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} i \in B}\\ {0,}&{{\rm{其他}}} \end{array}} \right. \end{array} $ | (4) |
其中:
路网是由传输路段与交叉口组建的网络系统,二者通信状态与稳定性共同决定着一个路网在社会经济效益中的贡献量.由于谱分析是针对链路的脆弱性分析方法,为了分析路网中的所有路段和交叉口,将G中的每个节点i分成两个新的节点i+, i-,得到无向辅助图G′ = (V′, E′, w′),G′中链路(i+, i-)对应G中的节点i,链路(j+, i-)对应G中的链路(j, i),V′、E′、w′分别代表G′中的节点集合、链路集合以及权重集合
| $ \left. {\begin{array}{*{20}{l}} {{V^\prime } = \{ {i^ + },{i^ - }|i \in V\} }\\ {{E^\prime } = \{ ({i^ + },{i^ - })|i \in V\} \cup \{ ({j^ + },{i^ - })|(j,i) \in E\} }\\ {{w^\prime }({i^ + },{i^ - }) = w(i),i \in V}\\ {{w^\prime }({j^ + },{i^ - }) = w(i,j),(i,j) \in E} \end{array}} \right\} $ | (5) |
其中G′中的所有链路代表G中所有节点和链路.
2.2 基于谱分析的路网脆弱性分析方法为考虑路网中的所有道路单元,将最具破坏性的瓶颈路段定义为道路容量小且可将路网分割成两个不可互通子网的路段,其中两个子网大小越接近,代表瓶颈路段拥堵后对路网连通性的破坏越大.在辅助图G′中对路网道路单元进行脆弱性分析,并识别出路网中易阻断路网连通性,造成路网大面积分割现象的瓶颈线路.公式(4)可转化为
| $ \begin{array}{*{20}{c}} {{\rm{min}}\frac{{\sum\limits_{i \in A,j \in B} {{w^\prime }} (i,j)}}{{V(A)V(B)}} = }\\ {\frac{1}{{V({G^\prime })}}\left( {\frac{{\sum\limits_{i \in A,j \in B} {{w^\prime }} (i,j)}}{{V(A)}} + \frac{{\sum\limits_{i \in A,j \in B} {{w^\prime }} (i,j)}}{{V(B)}}} \right)} \end{array} $ | (6) |
设
| $ {\rm{min}}\frac{{\sum\limits_{i \in A,j \in B} {{w^\prime }} (i,j)}}{{V(A)V(B)}} = \frac{1}{{V({G^\prime })}}{\rm{min}}{\kern 1pt} {\kern 1pt} {N_{{\rm{ cut }}}}(A,B) $ | (7) |
基于此,RNVS方案分析目标转化为最小化Ncut(A, B)的值.设x为一个N = |V′| = 2n维列向量,若节点i属于区域A,则x(i) = 1;否则节点i属于区域B,x(i) = -1.利用向量x可以将Ncut(A, B)写为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {N_{{\rm{ cut }}}}(A,B) = \frac{{\sum\limits_{i \in A,j \in B} {{w^\prime }} (i,j)}}{{V(A)}} + \frac{{\sum\limits_{i \in A,j \in B} {{w^\prime }} (i,j)}}{{V(B)}} = \\ \frac{{\sum\limits_{\mathit{\boldsymbol{x}}(i) > 0,\mathit{\boldsymbol{x}}(j) < 0} - w_{ij}^\prime \mathit{\boldsymbol{x}}(i)\mathit{\boldsymbol{x}}(j)}}{{\sum {(\mathit{\boldsymbol{x}}(} i) > 0)}} + \frac{{\sum\limits_{\mathit{\boldsymbol{x}}(i) < 0,\mathit{\boldsymbol{x}}(j) > 0} - w_{ij}^\prime \mathit{\boldsymbol{x}}(i)\mathit{\boldsymbol{x}}(j)}}{{\sum {(\mathit{\boldsymbol{x}}(} j) < 0)}} \end{array} $ | (8) |
其中w′ij = w′(i, j).向量x为将路网分割成2个子网的指标向量.由于x(i) = 1>0和x(i) = -1 < 0对方案目标的约束太强,致使求解满足公式(8)向量问题是一个NP-hard问题.为了放宽约束,采用(1+x)/2和(1-x)/2分别作为x(i)>0和x(i) < 0的代替向量.在辅助图G′中,V(A) = ∑(x(i)>0)表示子网A中的节点个数,V(B) = ∑(x(i) < 0)表示子网B中的节点个数,因此假设
| $ k = \frac{{\sum \mathit{\boldsymbol{x}} (i) > 0}}{{\left( {\sum \mathit{\boldsymbol{x}} (i) > 0} \right) + \left( {\sum \mathit{\boldsymbol{x}} (i) < 0} \right)}} $ |
通过以上定义与假设,4[Ncut(A, B)] = 4[Ncut(x)]转化为
| $ \begin{array}{*{20}{c}} {4\left[ {{N_{{\rm{ cut }}}}(\mathit{\boldsymbol{x}})} \right] = \frac{{{{(1 + \mathit{\boldsymbol{x}})}^{\rm{T}}}({\mathit{\boldsymbol{D}}_{{G^\prime }}} - {\mathit{\boldsymbol{M}}_{{G^\prime }}})(1 + \mathit{\boldsymbol{x}})}}{{k{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} + }\\ {\frac{{{{(1 - \mathit{\boldsymbol{x}})}^{\rm{T}}}({\mathit{\boldsymbol{D}}_{{G^\prime }}} - {\mathit{\boldsymbol{M}}_{{G^\prime }}})(1 - \mathit{\boldsymbol{x}})}}{{(1 - k){\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} = }\\ {\frac{{({\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_G}\mathit{\boldsymbol{x}} + {{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}{\bf{1}})}}{{k(1 - k){\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} + \frac{{2(1 - 2k){{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}\mathit{\boldsymbol{x}}}}{{k(1 - k){\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}}} \end{array} $ | (9) |
其中:LG′为图G′的Laplacian矩阵,向量1为n×1的全1向量.令α(x) = xTLG′x,β(x) = 1TLG′x,γ = 1TLG′1,且χ = xTx,可以进一步扩展方程(9)为
| $ \begin{array}{*{20}{c}} {4[{N_{{\rm{ cut }}}}(\mathit{\boldsymbol{x}})] = \frac{{(\alpha (\mathit{\boldsymbol{x}}) + \gamma ) + 2(1 - 2k)\beta (\mathit{\boldsymbol{x}})}}{{k(1 - k)\chi }} = }\\ {\frac{{(\alpha (\mathit{\boldsymbol{x}}) + \gamma ) + 2(1 - 2k)\beta (\mathit{\boldsymbol{x}})}}{{k(1 - k)\chi }} - }\\ {\frac{{2(\alpha (\mathit{\boldsymbol{x}}) + \gamma )}}{\chi } + \frac{{2\alpha (\mathit{\boldsymbol{x}})}}{\chi } + \frac{{2\gamma }}{\chi }} \end{array} $ | (10) |
根据矩阵DG′和矩阵MG′的矩阵元素值的设定可得,对于两矩阵的第h(1≤h≤2n,2n为辅助图G′的节点个数)行,矩阵DG′的行元素总和与矩阵MG′的行元素总和相等,因此根据矩阵的乘法规则可以得到γ = 1TLG′1 = 0,故式(10)的最后一项为0.式(10)可以进一步改写为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 4[{N_{{\rm{ cut }}}}(\mathit{\boldsymbol{x}})] = \\ \frac{{(1 - 2k + 2{k^2})(\alpha (\mathit{\boldsymbol{x}}) + \gamma ) + 2(1 - 2k)\beta (\mathit{\boldsymbol{x}})}}{{k(1 - k)\chi }} + \frac{{2\alpha (\mathit{\boldsymbol{x}})}}{\chi } = \\ \frac{{\frac{{(1 - 2k + 2{k^2})}}{{{{(1 - k)}^2}}}(\alpha (\mathit{\boldsymbol{x}}) + \gamma ) + \frac{{2(1 - 2k)}}{{{{(1 - k)}^2}}}\beta (\mathit{\boldsymbol{x}})}}{{\frac{k}{{1 - k}}\chi }} + \frac{{2\alpha (\mathit{\boldsymbol{x}})}}{\chi } \end{array} $ | (11) |
令b = k/(1-k),因为γ = 0,故式(11)变为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 4[{N_{{\rm{ cut }}}}(\mathit{\boldsymbol{x}})] = \\ \begin{array}{*{20}{c}} {\frac{{(1 + {b^2})(\alpha (\mathit{\boldsymbol{x}}) + \gamma ) + 2(1 - {b^2})\beta (\mathit{\boldsymbol{x}})}}{{b\chi }} + \frac{{2b\alpha (\mathit{\boldsymbol{x}})}}{{b\chi }} = }\\ {\frac{{(1 + {b^2})(\alpha (\mathit{\boldsymbol{x}}) + \gamma )}}{{bX}} + \frac{{2(1 - {b^2})\beta (\mathit{\boldsymbol{x}})}}{{b\chi }} + \frac{{2b\alpha (\mathit{\boldsymbol{x}})}}{{b\chi }} - \frac{{2b\gamma }}{{b\chi }} = } \end{array}\\ {\kern 1pt} {\kern 1pt} \frac{{(1 + {b^2})({\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_G}\mathit{\boldsymbol{x}} + {{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}{\bf{1}})}}{{b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} + \frac{{2b{\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}\mathit{\boldsymbol{x}}}}{{b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} - \frac{{2b{{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}{\bf{1}}}}{{b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} {\frac{{{{(1 + \mathit{\boldsymbol{x}})}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}(1 + \mathit{\boldsymbol{x}})}}{{b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} + \frac{{{b^2}{{(1 - \mathit{\boldsymbol{x}})}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}(1 - \mathit{\boldsymbol{x}})}}{{b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} - }\\ {\frac{{2b{{(1 - \mathit{\boldsymbol{x}})}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}(1 + \mathit{\boldsymbol{x}})}}{{b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}} = }\\ {\frac{{{{[(1 + \mathit{\boldsymbol{x}}) - b(1 - \mathit{\boldsymbol{x}})]}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}[(1 + \mathit{\boldsymbol{x}}) - b(1 - \mathit{\boldsymbol{x}})]}}{{b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}}}} \end{array} \end{array} $ | (12) |
设置y = (1+x)-b(1-x),可轻易发现
| $ {\mathit{\boldsymbol{y}}^{\rm{T}}}{\bf{1}} = \sum {(\mathit{\boldsymbol{x}}(} i) > 0) - b\sum {(\mathit{\boldsymbol{x}}(} i) < 0) = 0 $ | (13) |
因为
| $ \begin{array}{*{20}{c}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{y}} = \sum {(\mathit{\boldsymbol{x}}(} i) > 0) + {b^2}\sum {(\mathit{\boldsymbol{x}}(} i) < 0) = }\\ {b\sum {(\mathit{\boldsymbol{x}}(} i) < 0) + {b^2}\sum {(\mathit{\boldsymbol{x}}(} i) < 0) = }\\ {b\left( {\sum {(\mathit{\boldsymbol{x}}(} i) < 0) + b\sum {(\mathit{\boldsymbol{x}}(} i) < 0)} \right) = b{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}} \end{array} $ | (14) |
综合所有变量,可以将本文方案脆弱性分析目标转化为最优向量求解:
| $ \mathop {{\rm{min}}}\limits_x {N_{{\rm{ cut }}}}(\mathit{\boldsymbol{x}}) = \mathop {{\rm{min}}}\limits_y \frac{{{\mathit{\boldsymbol{y}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime}}}\mathit{\boldsymbol{y}}}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{y}}}} $ | (15) |
其中:y需要满足的条件是y(i)∈{1, -b},并且yT1 = 0.
由以上分析可以得出,脆弱性分析方案目标可转化为求使得式(15)最小化的最优向量y.由于图Laplacian矩阵LG′为半正定矩阵,故其最小特征值为0,y0 = {1, 1, …, 1}2n×1是LG′矩阵最小的特征值0对应的特征向量,且其所有的特征向量都相互正交,那么第2小的特征值对应的特征向量y1也是与y0正交的.利用瑞利商(Rayleigh quotient)[9]的一个性质:若Q是一个实对称矩阵,则其特征向量z与前r-1个最小的特征向量z1, …, zr-1都正交,那么商
根据瑞利商并结合式(4)及转化后的目标(式(8)和式(15)),可以得出图Laplacian矩阵的第2小特征值可量化路网当前脆弱程度;图Laplacian矩阵的第2小特征向量可实现RNVS方案脆弱元素的定位,第2小特征向量为
| $ {\mathit{\boldsymbol{y}}_1} = {\rm{arg}}\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{y}}^{\rm{T}}}{\mathit{\boldsymbol{y}}_0} = 0} \frac{{{\mathit{\boldsymbol{y}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{{G^\prime }}}\mathit{\boldsymbol{y}}}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{y}}}} $ | (16) |
在网络图的分割求解问题上,将脆弱性分析问题转化为求图Laplacian矩阵的特征值与特征向量,其中,第2小特征值可量化路网连通性脆弱程度(若第2小特征值为0,则代表网络图此时为断开状态),第2小特征值对应的特征向量y1为分割问题的解.在向量y1中选择一个分割数值(这里分割值为0),使y1中大于该数的部分所对应的节点放在子集A中,其余的放在子集B中,这样就将图G′分成两部分.将分割得到的元素集合映射回原始图G,得到脆弱元素集合S,即得到瓶颈线路.
3 基于连通贡献量的路网完善措施由RNVS方案分析结果可以得出,图Laplacian矩阵的第2小特征值可以量化路网连通性脆弱程度,因此,RNICC方案的目标为优化路网容量或拓扑结构,以提高第2小特征值的值.笔者从新建和扩建道路单元两方面提出了改善建议.
1) 扩建道路单元.对于识别出的脆弱交叉口,通过调节红路灯或扩建道路来降低事故或拥堵事件发生的概率;对于识别出的脆弱路段,通过改变路段结构或扩建道路来提高道路容量、降低拥堵概率.
2) 新建道路单元.通过在脆弱道路单元附近新建道路单元可以提高路网结构的鲁棒性,降低所识别出脆弱单元的紧急事件发生概率.此外,当脆弱单元因突发事件失效时,新建道路单元作为备用道路可以保证整个路网的连通性,进一步保证路网经济效益.针对最优路段新建,考虑到现实道路情况的距离及成本限制,RNICC方案旨在RNVS方案脆弱性分析结果周围进行道路新建,弥补网络脆弱性的同时,降低道路新建成本.新建路段的道路容量值为其两边交叉口中容量较大值,最优新建路段的选择目标为提高图Laplacian矩阵的第2小特征值.
采用式(17)代表新建链路对路网连通性的贡献量,具体表现为对于图Laplacian矩阵第2小特征值的提高程度:
| $ \varPhi (e) = \varPhi ({G^{ + e}}) - \varPhi (G) $ | (17) |
其中:Φ(G)为原始图G的辅助图的图Laplacian矩阵的第2小特征值,Φ(G+e)为增加链路后图的辅助图的图Laplacian矩阵的第2小特征值.
基于此,对于2.2节得到具体的脆弱元素集合S,新建路段确定步骤如下:
步骤1 node(S)为脆弱元素集合S中的节点集合,link(S)为S中的链路集合.
步骤2 在原始图G中,对于i∈node(S),确定其邻居交叉口集合ne(i).
步骤3 nlink_1 = {(i, j)|i∈node(S), j∈ne(i)}.
步骤4 在原始图G中,对于(u, v)∈link(S),确定节点u和v的邻居节点ne(u)和ne(v).
步骤5 nlink_2 = {(u, j)|j∈ne(u)}∪{(v, j)|j∈ne(v)}.
步骤6 nlink = nlink_1∪nlink_2.
步骤7 对于e∈nlink,确定max (Φ(e))作为新建链路,即新建路段.
4 仿真验证 4.1 简单例证考虑如图 2所示的具有6个节点(路口)和9个链路(路段)的简单路网模型图G,其中道路单元上的数字代表其车流容量(1 000辆/h).根据式(5)得到图G的辅助图G′. G′的图Laplacian矩阵的第2小特征值为0.82,对应的特征向量为[0.259 287 23, 0.425 274 6, 0.321 264 11, 0.390 615 39, -0.098 048 24, 0.078 969 11, -0.151 693 63, 0.077 198 33, -0.320 443 37, -0.242 591 38, -0.459 610 52, -0.280 221 62].

|
图 2 6-节点简单路网 |
由图Laplacian矩阵的第2小特征向量映射可得6-节点简单路网的脆弱道路单元为交叉口3和4,如图 3(a)所示.针对脆弱性分析结果,通过采用所提出的RNICC方案,定位的最优新建路段为链路(1, 6),如图 3(b)中的虚线所示.在备选路段集合nlink中这一链路对路网整体连通性贡献量最大,使得辅助图的图Laplacian矩阵的第2小特征值变为1.204,提高了46.8%.
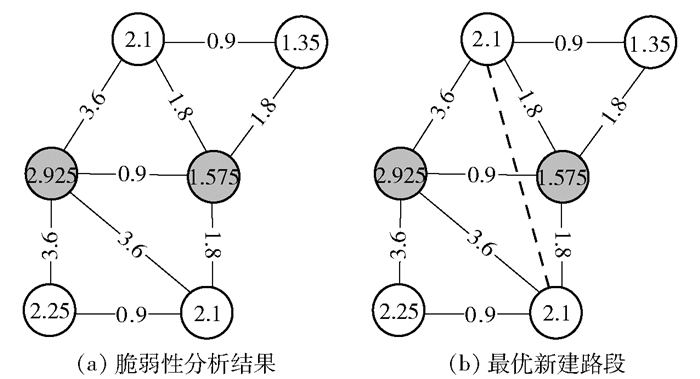
|
图 3 6-节点路网脆弱性分析结果与最优新建路段 |
以2个真实路网实例为例,进行方案有效性验证.分别选取Sioux falls路网及杭州市上城区西湖东侧某区域城市路网作为研究对象.
1) Sioux falls路网
Sioux falls路网是一个中等规模且广泛用于学术研究的经典网络[10],该路网有24个节点,38条边.简化后的路网如图 4所示,圆圈内的数字代表节点编号,Sioux falls路网道路容量源于文献[11]. Sioux falls路网具有较为完备的道路基础数据,包括路段长度、车道数、通行容量等,因此被广泛采用作为案例分析网络.
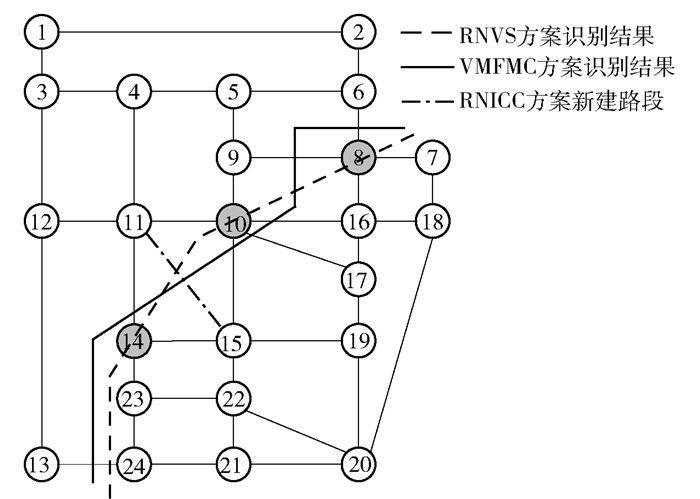
|
图 4 Sioux falls路网及不同方案识别结果 |
选用基于最大流-最小割的脆弱性分析方法(VMFMC, vulnerability analysis method based on maximum flow-minimum cut)作为对比方案. RNVS方案切割总容量为25.24(1 000辆/h),VMFMC方案切割总容量为38.23(1 000辆/h).从切割容量值可以看出,相比于VMFMC方案,RNVS方案识别出路网中的瓶颈线路.由于式(4)中的cut(A, B)可以量化方案脆弱性分析的准确程度,VMFMC方案的分析结果(cut(A, B)值)为0.067,RNVS方案的分析结果(cut(A, B)值)为0.044,因此,RNVS方案脆弱性分析更加准确,识别出路网中可对路网造成大面积切割的瓶颈线路.此外,图中短虚线链路(11, 15)为RINCC方案所识别出的最优新建路段,新链路的添加使得辅助图的图Laplacian矩阵的第2小特征值提高了9.68%.
2) 杭州市某区域路网
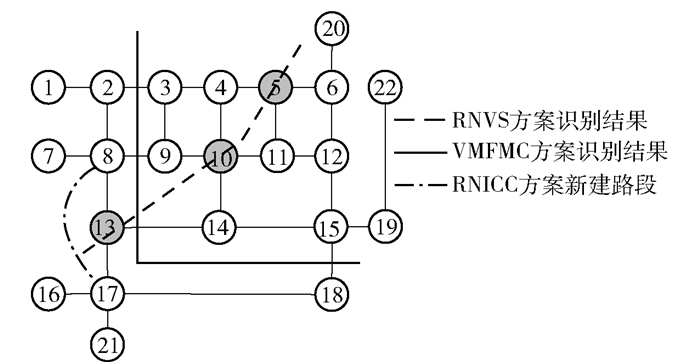
以杭州市上城区西湖东侧某区域城市道路网络为例进行算法验证.该道路网络由22个节点和28条链路组成,其区域区位图如图 5所示.研究区域路网简化图及算法方案对比结果如图 6所示,其中道路单元容量数据来源于《杭州市道路交通车流量汇总表》.
|
图 5 杭州市上城区西湖东侧某区域城市路网区位图 |
|
图 6 杭州市某区域路网简化图及不同方案识别结果 |
通过计算及分析可知:首先,RNVS方案分析结果切割总容量为1 127.5(辆/h),对比方案VMFMC分析结果切割总容量为1 864(辆/h).显见,RNVS方案能够识别出路网中的瓶颈线路.其次,VMFMC方案分析结果cut(A, B)值为3.983,RNVS方案分析结果cut(A, B)值为2.456.因此,笔者所提方案脆弱性分析更加准确.最后,RINCC方案能够识别出的最优新建路段为(8, 17),新链路的添加使得辅助图的图Laplacian矩阵的第2小特征值提高了34.1%.
5 结束语对于道路交通网络,网络整体连通性是路网实现基本传输功能的基本保障,也是笔者关注的核心问题之一.针对现有关于路网脆弱性分析的研究中脆弱道路单元分析不全面的问题,所提出的RNVS方案可有效识别出路网中的瓶颈线路.此外,针对瓶颈路线易拥堵从而造成的路网连通性破坏问题,所提出的RNICC方案可在脆弱道路单元周围识别出最优新建路段,进而提高路网结构鲁棒性.综上,所提方案可为路网结构分析、规划和鲁棒性优化提供准确指导.
| [1] |
Chakraborty O, Das A, Dasgupta A, et al. A multi-objective framework for analysis of road network vulnerability for relief facility location during flood hazards:A case study of relief location analysis in Bankura District, India[J]. Transactions in GIS, 2018, 22(5): 1064-1082. DOI:10.1111/tgis.12314 |
| [2] |
Faturechi R, Miller-Hooks E. Measuring the performance of transportation infrastructure systems in disasters:a comprehensive review[J]. Journal of Infrastructure Systems, 2014, 21(1): e04014025-e04014025. |
| [3] |
Mattsson L G, Jenelius E. Vulnerability and resilience of transport systems-A discussion of recent research[J]. Transportation Research Part A:Policy and Practice, 2015, 81: 16-34. DOI:10.1016/j.tra.2015.06.002 |
| [4] |
Chen B Y, Lam W H K, Sumalee A, et al. Vulnerability analysis for large-scale and congested road networks with demand uncertainty[J]. Transportation Research Part A:Policy and Practice, 2012, 46(3): 501-516. DOI:10.1016/j.tra.2011.11.018 |
| [5] |
李彦瑾, 罗霞, 车国鹏. 突发拥挤条件下城市道路网脆弱性识别[J]. 公路交通科技, 2017, 34(5): 129-136. Li Yanjin, Luo Xia, Che Guopeng. Vulnerability identification of urban road network under abrupt congestion condition[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 129-136. |
| [6] |
Bell M G H, Kurauchi F, Perera S, et al. Investigating transport network vulnerability by capacity weighted spectral analysis[J]. Transportation Research Part B:Methodological, 2017, 99: 251-266. DOI:10.1016/j.trb.2017.03.002 |
| [7] |
Reggiani A, Nijkamp P, Lanzi D. Transport resilience and vulnerability:the role of connectivity[J]. Transportation Research Part A:Policy and Practice, 2015, 81: 4-15. DOI:10.1016/j.tra.2014.12.012 |
| [8] |
Akbarzadeh M, Reihani S F S, Samani K A. Detecting critical links of urban networks using cluster detection methods[J]. Physica A:Statistical Mechanics and Its Applications, 2019, 515: 288-298. DOI:10.1016/j.physa.2018.09.170 |
| [9] |
Golub G H, Van Loan C F. Matrix computations[M]. Baltimore: JHU Press, 2012: 50-495.
|
| [10] |
LeBlanc L J. An algorithm for the discrete network design problem[J]. Transportation Science, 1975, 9(3): 183-199. |
| [11] |
张树德.基于复杂网络理论的城市道路网络脆弱性研究[D].哈尔滨: 哈尔滨工业大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014083737.htm
|



