为了提高易受视距(LOS)和非视距(NLOS)传输影响无线应用的性能,对大规模三维多输入多输出(3D MIMO)系统中的LOS/NLOS识别进行了研究,针对实际场景,采用实际信道而非通常假设的理想准确信道,提出了一种改进的时-空-频信道相关识别算法TSFCI-1.识别过程包括3个阶段:根据LOS/NLOS用户不同的时-空-频特性定义测量;针对大规模3D MIMO中信道空间相关性不平稳的特点,对评价指标在空间间隔上求期望;使用时域信道信息进行建模和识别.在此基础上,考虑到天线双极化的影响,改进评价指标,并提出算法TSFCI-2.仿真结果表明,TSFCI-1和TSFCI-2的算法性能均优于对比算法6%以上,错误率分别低至1.92%和1.72%.此外,讨论了信噪比和时域径数对表现最好的TSFCI-2性能的影响.
To improve the performance of some wireless technologies, which are susceptible to line of sight (LOS) and non line of sight (NLOS), LOS/NLOS identification in 3D massive multi-input multi-output (MIMO) system is studied. Based on channel correlation, an improved identification algorithm, TSFCI-1, is proposed, which uses actual channel information instead of the normally assumed ideal accurate channel. The process includes:defining measurement based on time-space-frequency properties of LOS/NLOS; in view of the unsteady spatial channel correlation for 3D massive MIMO systems, finding the expectation of measurement on the spatial interval; using channel information to construct the statistical identification model. Considering the influence of antenna dual-polarization, TSFCI-2 with better evaluation index is proposed. It is shown that the identification error of TSFCI-1 and TSFCI-2 is as low as 1.92% and 1.72%, with over 6% better than a previous study. Besides, the effects of signal to noise ratio and the taps number on TSFCI-2 with the best performance is discussed.
大规模三维多输入多输出(3D MIMO,3-dimensional multiple-input multiple-output)是第5代移动通信系统的关键技术,但该场景下视距/非视距(LOS/NLOS,line-of-sight/non-line-of-sight)识别未得到足够认识. LOS径在多径中占主导地位,但无线传输以NLOS为特征.在基于码本的开环波束赋形和空间约束大规模MIMO[1-2]场景下,LOS/NLOS会对良好传播造成影响,用户信道正交性[3]也与此密切相关.因此,准确识别LOS/NLOS对上述无线应用的性能提升十分必要.
相关技术在不同场景下已被提出.魏思菁等[4]提出了一种基于仿射传播聚类的LOS/NLOS的方法. Xu等[5]利用信道相关模型来进行MIMO-OFDM系统的LOS/NLOS识别. Zeng等[6]使用卷积神经网络模型分析了抽头能量矩阵,并识别LOS/NLOS.然而,以上工作存在3个问题:1)研究场景与大规模3D MIMO具有不同特征,原算法性能受限;2)需对信道信息进行额外处理,增加了开销;3)假设基站知道准确信道信息,实用性差.文献[6]中所提技术虽适用大规模3D MIMO场景,但机器学习技术使算法复杂度过高,现阶段基站处理能力很难达到要求.
针对以上问题,提出了基于时-空-频信道相关的识别算法-1(TSFCI-1,time-space-frequency correlation identification-1),并针对天线阵列交叉极化特性,提出改进的时空频相关识别算法-2(TSFCI-2,time-space-frequency correlation identification-2).在构建识别模型时,考虑了3D MIMO系统信道相关与空间分离不平稳的特性,避免了额外处理造成的开销,且使用估计信道信息进行识别,相比以往假设基站知道准确信道信息的工作,更具实用意义.
对3D MIMO系统的信道相关模型和采用的信道估计方法进行了介绍,提出了2种改进的LOS/ NLOS识别方案,说明了其识别原理,最后给出了仿真结果的对比分析,并讨论了一些影响因素.
1 系统模型、信道模型及相关方法 1.1 3D MIMO系统模型仿真场景是单个城市宏小区,信道模型参数由第3代合作伙伴计划(3GPP,3rd generation partnership project)[7]的大规模3D MIMO模型指定.
在3GPP的大规模3D MIMO系统中,用户属于LOS或NLOS的概率与该用户和基站之间的距离密切相关.某用户是LOS用户的概率,表示为
| $ \begin{array}{*{20}{c}} {{P_L} = {\rm{min}}\left( {\frac{{18}}{{{d_{{\rm{2D}}}}}},1} \right)(1 - {{\rm{e}}^{ - \frac{{{d_{{\rm{2D}}}}}}{{63}}}}) + {{\rm{e}}^{ - \frac{{{d_{{\rm{2D}}}}}}{{63}}}}(1 + }\\ {C({d_{{\rm{2D}}}},{h_{{\rm{UT}}}}))} \end{array} $ | (1) |
如果假设用户高度hUT都为0,且用户-基站2D距离d2D均大于18 m,则C(d2D, hUT) = 0,那么有
| $ {P_L} = \frac{{18}}{{{d_{{\rm{2D}}}}}} + {{\rm{e}}^{ - \frac{{{d_{{\rm{2D}}}}}}{{63}}}}\left( {1 - \frac{{18}}{{{d_{{\rm{2D}}}}}}} \right) $ | (2) |

|
图 1 笛卡儿坐标系中球面角和球单位向量的定义 |
在仿真的散射模型中,任意2个多径对应的簇的位置和大小不相关,不同多径的相关系数相互独立,则发射天线单元p与接收天线单元q间的信道系数为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}^{p,q}}(l,t) = \sum\limits_{g = 1}^G {\sqrt {{P_{l,g}}} } \{ {c_{p,q,l,g}} \times }\\ {{\rm{exp}}({\rm{j}}2\pi {\lambda ^{ - 1}}{\mathit{\boldsymbol{d}}_p}{\mathit{\boldsymbol{\xi }}_{l,g}}) \times }\\ {{\rm{exp}}({\rm{j}}2\pi {\lambda ^{ - 1}}{\mathit{\boldsymbol{d}}_q}{\mathit{\boldsymbol{\psi }}_{l,g}}) \times }\\ {\quad {\rm{exp}}({\rm{j}}2\pi {\nu _{l,g}}t)\} } \end{array} $ | (3) |
其中:λ表示载波波长;G为每个多径包含的子径数;Pl, g指子径(l, g)的能量,l和g分别指多径和其中的子径;cp, q, l, g是由发射和接收天线结构以及初始随机相位产生子径(l, g)的系数.当发射天线单元之间相距很近时,对于相同偏振下所有的发射天线单元,都有cp, q, l, g≈cq, l, g.此外,νn, g表示子径(l, g)的多普勒频率分量,dp和dq分别为发射和接收天线单元p与q的位置矢量;ξl, g和ψl, g分别为离开角和到达角联合向量.
1.2 时间-空间-频率相关模型使用的时间-空间-频率信道相关模型在一定程度上参考了文献[5],并结合大规模3D MIMO进行了修正.对于一个上行传输发射和接收天线单元数分别为Gt和Gr的3D MIMO系统,其信道冲激响应(CIR,channel impulse response)可以被表示为一个抽头延迟线模型,即
| $ {h^{p,q}}(t,\tau ) = \sum\limits_{l = 1}^L {a_l^{p,q}} (t)\delta (\tau - {\tau _l}) $ | (4) |
其中:alp, q(t)为第l条多径分量的幅度系数,τl为对应的到达时间.
在3D MIMO信道模型中,假设用户只在水平方向以较低速度运动,则LOS分量asp, q(t)可以表示为
| $ \begin{array}{*{20}{c}} {a_s^{p,q}(t) = {A^{p,q}}{\rm{exp}}( - {\rm{j}}2\pi (p - 1){d_t}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _l}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _l}) \times }\\ {{\rm{exp}}( - {\rm{j}}2\pi (q - 1){d_r}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _l}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _l}) \times }\\ {{\rm{exp}}({\rm{j}}2\pi {f_D}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ({\vartheta _l}){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ({\varphi _l} - {\varphi _\alpha })t)} \end{array} $ | (5) |
其中:Ap, q代表幅度的常数;dt和dr分别为发射和接收天线单元间距;对于第l条多径,ϕl、θl、φl和ϑl分别为其离开角(AOD,angle of departure)和到达角(AOA,angle of arrival)的方位角和仰角,fD为最大多普勒频率;φα表示移动方向.
对式(4)应用离散傅里叶变换(DFT,discrete fourier transform),有子载波n的信道频率响应为
| $ {\mathit{\boldsymbol{H}}^{p,q}}(n,t) = \sum\limits_{l = 1}^L {a_l^{p,q}} (t){\rm{exp}}( - {\rm{j}}2\pi n\Delta f{\tau _l}) $ | (6) |
其中:Δf为频率间隔,n = 1, 2, …, N-1,N为子载波总数.
Hp1, q1(n1, t)和Hp2, q2(n2, t+Δt)的时间-空间-频率信道相关性可以表示为
| $ \begin{array}{*{20}{c}} {R({p_1},{p_2},{q_1},{q_2},{n_1} - {n_2},\Delta t) \buildrel \Delta \over = }\\ {E\left\{ {{\mathit{\boldsymbol{H}}^{{p_1},{q_1}}}({n_1},t){{[{\mathit{\boldsymbol{H}}^{{p_2},{q_2}}}({n_2},t + \Delta t)]}^{\rm{H}}}} \right\}} \end{array} $ | (7) |
利用式(6),则式(7)中的相关性在频域可表示为
| $ \begin{array}{*{20}{c}} {R({p_1},{p_2},{q_1},{q_2},{n_1} - {n_2},\Delta t) \buildrel \Delta \over = }\\ {\sum\limits_{l = 1}^L E \{ a_l^{{p_1},{q_1}}(t){{[a_l^{{p_2},{q_2}}(t + \Delta t)]}^*}\} \times }\\ {{\rm{exp}}( - {\rm{j}}2\pi \Delta f({n_1} - {n_2}){\tau _l})} \end{array} $ | (8) |
在文献[5]中,Hp, q(n, t)在子载波分离、时间分离和空间分离上均是广义平稳的.在该场景中,式(8)中E{alp1, q1(t)[alp2, q2(t+Δt)]*}是p1-p2和q1-q2的函数[8],但3D MIMO系统中,随天线规模增大,不同天线对之间的信道矩阵相关系数与空间分离并不完全平稳[9],针对这一特性,笔者提出一种改进的算法来适应大规模3D MIMO场景,以获得更好的识别性能.
1.3 基于IDFT的信道估计方法为了使研究更加具有实际意义,考虑到现实中基站无法获知准确的信道信息,突破性地将使用基于反离散傅里叶变换(IDFT,inverse discrete fourier transform)的信道估计方法获得的信道用于LOS/NLOS识别,而非前人工作中使用的真实信道.
仿真考虑了路径损耗及噪声.在大规模3D MIMO中,LOS/NLOS有不同的路径损耗模型[7],噪声为高斯白噪声,具体的信道估计过程如下.
假设使用探测参考信号(SRS,sounding reference signal)导频序列同时对U个UE进行信道估计,UE以低速移动,且认为一个子帧内信道不变,因此在预处理中只取一个抽样点.为了避免引入符号间干扰,影响对算法性能的分析,舍去超过循环前缀的径.通过快速傅里叶变换(FFT,fast fourier transform)得到频域信道,模拟现实中导频发射-传播-接收的过程,则频域信道可表示为
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{XH}} + \mathit{\boldsymbol{W}} = \sum\limits_{u = 1}^U {{\mathit{\boldsymbol{X}}_u}} {\mathit{\boldsymbol{H}}_u} + \mathit{\boldsymbol{W}} $ | (9) |
其中Y为接收到的导频向量,X为元素为发送导频信号的对角阵,第u个UE的SRS导频序列可以表示为
最小平方(LS,least squares)频域信道估计算法被用于对接收信号进行第一步处理,即对式(9)中的H进行估计,求
| $ \mathit{\boldsymbol{J}} = {(\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{\hat Y}})^{\rm{H}}}(\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{\hat Y}}) = {(\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{X\hat H}})^{\rm{H}}}(\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{X\hat H}}) $ | (10) |
其中:
| $ \mathit{\boldsymbol{\hat H}} = {\mathit{\boldsymbol{X}}^{ - 1}}\mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{H + }}{\mathit{\boldsymbol{X}}^{ - 1}}\mathit{\boldsymbol{W}} $ | (11) |
但是,由于LS估计算法在估计时忽略了噪声的影响,所以在此基础上还需要进行去噪.结合式(9),有
| $ \mathit{\boldsymbol{X}}_u^{\rm{H}}\mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{H}}_u} + \sum\limits_{j \ne u}^K {{\mathit{\boldsymbol{H}}_u}} {{\rm{e}}^{{\rm{j}}({\omega _j} - {\omega _u})}} + \mathit{\boldsymbol{X}}_u^{\rm{H}}\mathit{\boldsymbol{W}} $ | (12) |
利用离散傅里叶反变换,可获得用户设备(UE,user equipment)u的抽头能量分布,即时域信道矩阵
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat h}}(l) = {{\mathit{\boldsymbol{\hat h}}}_u}(l) + \mathit{\boldsymbol{\hat W}}(l) + }\\ {\sum\limits_{j \ne u}^U {{{\mathit{\boldsymbol{\hat h}}}_j}} \left( {l + |{\omega _j} - {\omega _u}|\frac{M}{8}} \right)} \end{array} $ | (13) |
其中
| $ {Z_u}(l) = \left\{ {\begin{array}{*{20}{l}} {0,}&{l > {M_u}{\rm{ 或 }}|{\mathit{\boldsymbol{h}}_u}(l)| < {P_u}}\\ {1,}&{{\rm{其他}}} \end{array}} \right. $ | (14) |
其中:
大规模3D MIMO场景下,由于天线阵列布局和天线数目的变化,不同天线对之间信道相关性与空间分离不再完全平稳,因此考虑构建一个基于时间-空间-频率信道相关的数学统计模型,在处理时对选取的每对天线对之间的模型值求取期望,将LOS/NLOS的信道特征直观的区分开来;此外,不同于以往工作中假设基站知道准确的信道信息,研究突破性地模拟现实应用场景,让基站使用估计信道用于LOS/NLOS识别,以此使提出的算法能够在大规模3D MIMO场景中获得更好识别性能的同时,也更具实际意义.
2.2 算法步骤及分析在大规模3D MIMO系统中,对于第l条多径有
| $ \begin{array}{l} \rho ({p_1},{p_2},{q_1},{q_2},{n_1} - {n_2},\Delta t) \buildrel \Delta \over = \\ \frac{{R({p_1},{p_2},{q_1},{q_2},{n_1} - {n_2},\Delta t)}}{{[R({p_1},{p_1},{q_1},{q_1},0,0) + R({p_2},{p_2},{q_2},{q_2},0,0)]/2}} = \\ \frac{{\mathop \sum \limits_{l = 1}^L {R_{{a_l}}}({p_1},{p_2},{q_1},{q_2},\Delta t){\rm{exp}}( - {\rm{j}}2\pi \Delta f({n_1} - {n_2}){\tau _l})}}{{\mathop \sum \limits_{l = 1}^L \left[ {{R_{{a_l}}}({p_1},{p_1},{q_1},{q_1},0) + {R_{{a_l}}}({p_2},{p_2},{q_2},{q_2},0)} \right]/2}} \end{array} $ | (15) |
当用户存在LOS路径时,
根据式(5),有
| $ \begin{array}{*{20}{c}} {{R_{{a_s}}}({p_1},{p_2},{q_1},{q_2},\Delta t) = }\\ {\sigma _s^2{\rm{exp}}( - {\rm{j}}2\pi ({p_1} - {p_2}){d_t}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _l}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _l}) \times }\\ {{\rm{exp}}( - {\rm{j}}2\pi ({q_1} - {q_2}){d_r}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _l}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _l}) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}({\rm{j}}2\pi {f_D}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ({\vartheta _l}){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ({\varphi _l} - {\varphi _\alpha })\Delta t)} \end{array} $ | (16) |
其中σs2是LOS分量的能量.
提出的LOS/NLOS识别模型可以表示为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varGamma (N/2) \buildrel \Delta \over = E[\left| {\rho ({p_1},{p_2},{q_1},{q_2},N/2,\Delta t)} \right|] = \\ {\rm{E}}\left[ {\frac{{\left| {\sum\limits_{l = {\rm{ }}2k - 1} {{R_{{a_l}}}({p_1},{p_2},{q_1},{q_2},\Delta t) - \sum\limits_{l = {\rm{ }}2k} {{R_{{a_l}}}({p_1},{p_2},{q_1},{q_2},\Delta t)} } } \right|}}{{\mathop \sum \limits_{l = 1}^L \left[ {{R_{{a_l}}}({p_1},{p_1},{q_1},{q_1},0) + {R_{{a_l}}}({p_2},{p_2},{q_2},{q_2},0)} \right]/2}}} \right] \end{array} $ | (17) |
由于Hp, q(n, t)相对子载波分离是平稳的,为了方便研究,考虑n1-n2 = N/2,那么式(8)中的指数项有exp (-j2πΔf(n1-n2)τl) = exp (-jπ(l-1)) = (-1)l-1,其中τl = (l-1)/B.因此式(11)中的第2个等式可由第1个等式展开获得,故模型从理论上成立.
在仿真的系统中,每个用户只有一根天线,即Mt = 1,因此信道相关R(p1, p2, q1, q2, n1-n2, Δt)与ρ(p1, p2, q1, q2, n1-n2, Δt)分别可以简化为R(q1, q2, n1-n2, Δt)及ρ(q1, q2, n1-n2, Δt),则有
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varGamma (N/2) \buildrel \Delta \over = E[\left| {\rho ({q_1},{q_2},\Delta t)} \right|] = \\ {{E}}\left[ {\frac{{\left| {\sum\limits_{l = {\rm{ }}2,i - 1} {{R_{{a_l}}}({q_1},{q_2},\Delta t) - \sum\limits_{l = {\rm{ }}2k} {{R_{{a_l}}}({q_1},{q_2},\Delta t)} } } \right|}}{{\mathop \sum \limits_{l = 1}^L \left[ {{R_{{a_l}}}({q_1},{q_1},0) + {R_{{a_l}}}({q_2},{q_2},0)} \right]/2}}} \right] \end{array} $ | (18) |
从上述模型可以引申出2种具体的识别算法TSFCI-1和TSFCI-2.其中,对于TSFCI-1,考虑在计算数学期望时,对其所有相邻天线之间的相关性求期望,以解决不同天线对之间信道相关性不同导致的识别性能较差的问题.此外,由于仿真中基站天线是交叉极化的,所以对于TSFCI-2,当计算模型中的数学期望时,可以使选取的每一对对应的q1和q2都是同一天线2个不同的极化方向. 2种算法具体的表示将在第3节中给出.
3 LOS/NLOS识别算法实现定义
| $ \begin{array}{*{20}{l}} {{\varGamma _{{\rm{LOS}}}}(N/2) = \frac{1}{{{G_{\rm{r}}} - 1}}\sum\limits_{q = 1}^{q = {G_{\rm{r}}} - 1} \quad Ƴ_{{\rm{LOS}}}^{q,q + 1}(N/2)}\\ {{\varGamma _{{\rm{NLOS}}}}(N/2) = \frac{1}{{{G_{\rm{r}}} - 1}}\sum\limits_{q = 1}^{q = {G_{\rm{r}}} - 1} {Ƴ_{{\rm{NLOS}}}^{q,q + 1}} (N/2)} \end{array} $ | (19) |
其中q表示基站天线.
对于算法TSFCI-2,在计算模型Γ(N/2)中的期望时,令q1-q2 = 1及q1 = 2, 4, …, Gr.将第k个基站天线表示为qk,对于LOS和NLOS条件,算法模型Γ(N/2)分别可以表示为
| $ \begin{array}{*{20}{l}} {{\varGamma _{{\rm{LOS}}}}(N/2) = \frac{1}{{{G_{\rm{r}}}/2}}\sum\limits_{k = 1}^{{G_{\rm{r}}}/2} \quad Ƴ_{{\rm{LOS}}}^{{q_{2k}},{q_{2k - 1}}}(N/2)}\\ {{\varGamma _{{\rm{NLOS}}}}(N/2) = \frac{1}{{{G_{\rm{r}}}/2}}\sum\limits_{k = 1}^{{G_{\rm{r}}}/2} {Ƴ_{{\rm{NLOS}}}^{{q_{2k}},{q_{2k - 1}}}} (N/2)} \end{array} $ | (20) |
在LOS的情况下,LOS分量的相关系数Ral(q1, q2, Δt)有一个确定的值σs2,该值是不会随着时间和空间间隔改变的,那么有
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{lim}}}\limits_{\Delta t \to \infty {\kern 1pt} {\kern 1pt} {\rm{or}}{\kern 1pt} {\kern 1pt} ({q_1} - {q_2}) \to \infty } Ƴ_{{\rm{LOS}}}^{{q_1},{q_2}}(N/2) = \\ \frac{{\sigma _s^2}}{{\sum\limits_{l = 1}^L {\frac{{{R_{{a_l}}}({q_1},{q_1},0) + {R_{{a_l}}}({q_2},{q_2},0)}}{2}} }} \end{array} $ | (21) |
在NLOS的情况下,相干时间和相关距离一般被认为是相当小的.因此,相比LOS条件下,对于典型的空间分离q1-q2≥1,Ral(q1, q2, Δt)被认为是更小的.一般来说,当时间分离远大于相干时间或者空间分离远大于相关距离时,可以认为对应的相关系数近似为0,即
| $ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{lim}}}\limits_{\Delta t \to \infty {\kern 1pt} {\kern 1pt} {\rm{or}}{\kern 1pt} {\kern 1pt} ({q_1} - {q_2}) \to \infty } Ƴ_{{\rm{NLOS}}}^{{q_1},{q_2}}(N/2) = 0 $ | (22) |
基于以上分析,Υq1, q2(N/2)背后隐藏的意义就在于LOS的情况下,模型式(15)的分子约等于σs2,而NLOS的情况下,模型分子显著小于LOS情况.因此,对于某个时间或者空间分离,有ΥLOSq1, q2(N/2)>ΥNLOSq1, q2(N/2).
因此,结合式(19)、式(20),可以得到大规模3D MIMO系统中识别LOS/NLOS的关键,对于TSFCI-1和TSFCI-2,均可以表示为
| $ {\varGamma _{{\rm{LOS}}}}(N/2) > {\varGamma _{{\rm{NLOS}}}}(N/2) $ | (23) |
通过式(23),即可判断一个用户是否处于LOS条件下.
由于实际中不能达到Δt→∞or(q1-q2)→∞,所以式(21)、式(22)只用于从理论上说明算法实现原理,仿真结果还要基于式(19)、式(20)进行分析.
4 仿真结果在3D MIMO场景中,对所提方案和对比算法进行了仿真.参数选择遵从3GPP协议,主要参数如下.
假设抽头功率指数衰减,即εl2 = exp (-τl/τrms),每个K因子使用5万用户数据用于建模.
|
|
表 1 参数表格 |
对于LOS情况,第1条多径是视距分量和色散分量的和,即
在仿真中,为了避免引入符号间干扰,舍弃超过循环前缀的径,即时域径数Ml≤144.令Ml = 144,SNR为0,Gr = 64.识别示意如图 2所示,NLOS识别错误率PF和LOS识别错误率PM如表 2所示.
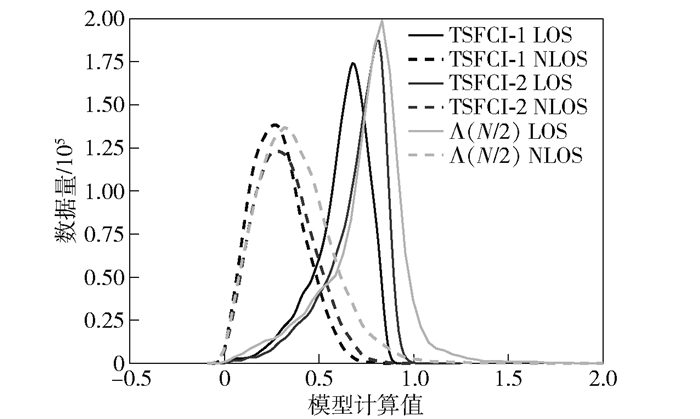
|
图 2 TSFCI-1、TSFCI-2、Λ(N/2)模型分布(κ = 0) |
|
|
表 2 算法识别错误率对照表 |
因K因子呈正态分布,算法识别错误率期望为
| $ {P_e}(\kappa = 0) = {P_F}(\kappa = 0){P_{{\rm{NLOS}}}} + {P_M}(\kappa = 0){P_{{\rm{LOS}}}} $ | (24) |
| $ E[{P_e}(\kappa )] = \int {\frac{1}{{\sqrt {2\pi } {\sigma _\kappa }}}} {P_e}(\kappa ){\rm{exp}}\left( {\frac{{{{(\kappa - \mu )}^2}}}{{2\sigma _\kappa ^2}}} \right){\rm{d}}\kappa $ | (25) |
其中μ与σκ分别为K因子的均值和标准差. Λ(N/2)、TSFCI-1和TSFCI-2的识别错误率期望分别为8.06%、1.92%、1.72%.由于考虑了大规模3D MIMO系统中信道矩阵相关系数在空间间隔上的不平稳,所以所提算法性能优于对比算法.
从表 2可见,3种方法的性能都随着K因子的增大而获得提升.如式(21)、式(22)所示,K因子越大,计算的LOS测度越大,而NLOS测度不变.这使得两者测度分布之间的差距变得更大,从而减少了识别误差.
此外,与TSFCI-1计算所有相邻天线相关性期望不同,TSFCI-2只计算同一天线不同极化方向的期望,由式(21)、式(22)可知,其LOS测度大于TSFCI-1,因此模型分布差距比TSFCI-1更大.但因为q1-q2 = 1,即只考虑相邻天线,且天线间距较小,所以相关性变化不大,性能相差较小.此外,TSFCI-2运算量仅为TSFCI-1的1/2,因此TSFCI-2的综合性能优于TSFCI-1.
4.2 SNR对TSFCI-2性能的影响在工作中,还选取了综合性能最好的TSFCI-2算法,讨论了信噪比(SNR,signal to noise ratio)对其性能的影响.令Gr = 64,Ml = 144.仿真结果如图 3所示.
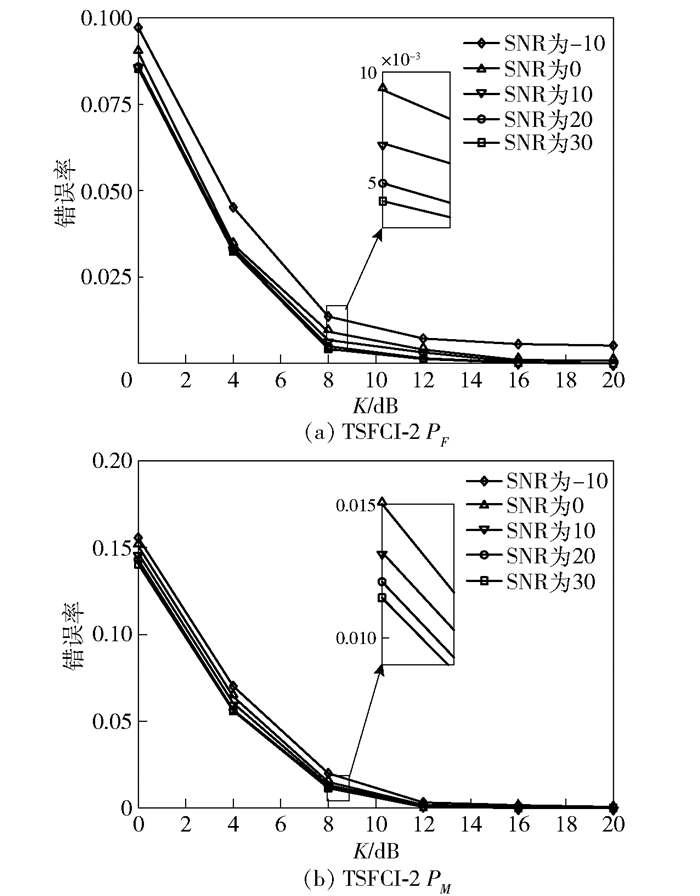
|
图 3 TSFCI-2识别NLOS错误率PF和LOS错误率PM |
当SNR较小(-10, 0)时,随着SNR的提高,算法的性能会有一定程度的提升;SNR较大(10, 20, 30)时,性能没有明显提升.即在一定范围内,随着SNR从小到大,识别性能呈现一个先提升再逐渐趋于平缓的趋势.
出现这种现象的原因如下:当SNR较小时,有用信号能量远小于噪声能量,去噪过程难以区分噪声和有效信号,这导致信道估计误差大,原有的LOS/NLOS用户信道特征变得模糊,区分困难.而随着SNR变大,信道估计更加准确,算法性能得到提升.但当SNR不断增大,信道估计准确度到达极限,且去噪过程会除去能量较小的径,保留能量较大的径,此时,随着SNR继续增大,识别性能趋于平稳.
4.3 时域径数对TSFCI-2性能的影响讨论了时域径数对TSFCI-2性能的影响.令Gr = 64,SNR为0,Ml = 6, 12, 24, 72,144,仿真结果如图 4所示.

|
图 4 TSFCI-2识别NLOS错误率PF和LOS错误率PM |
径数为6~12时,算法性能明显提高;径数为12~144时,性能提升逐渐变小,直至趋于平稳.总体来看,径数对算法性能的影响较小.一定范围内,径数增多使得用于模型计算的径增多,LOS/NLOS的分布区分更明显,性能得到提高;但当径数继续增加,由于新增径能量较小或已被去噪过程置零,对算法性能不再有明显影响.综合考虑识别过程的计算量与识别准确率,建议时域径数选为12.
5 结束语针对大规模3D MIMO中不同天线对之间的信道相关差异,提出了TSFCI-1和TSFCI-2两种基于时-空-频信道相关性的改进LOS/NLOS识别算法,并在识别中突破性地采用了估计信道信息.仿真结果表明,TSFCI-1和TSFCI-2的识别错误率分别低至1.92%和1.72%,均比对比算法降低了6%以上.另外,随着SNR的提高,TSFCI-2的性能呈现先提升再趋于平缓的趋势.综合考虑识别方案的效率和准确性,时域径数选择12较为合理.该方法可以显著提高定位系统等无线应用的性能,有利于信道相关性的研究.
| [1] |
Aditya S, Molisch A F, Behairy H M. A survey on the impact of multipath on wideband time-of-arrival based localization[J]. Proceedings of the IEEE, 2018, 106(7): 1183-1203. DOI:10.1109/JPROC.2018.2819638 |
| [2] |
Masouros C, Matthaiou M. Space-constrained massive MIMO:hitting the wall of favorable propagation[J]. IEEE Commun Lett, 2015, 19(5): 771-774. DOI:10.1109/LCOMM.2015.2409832 |
| [3] |
Gao X, Edfors O, Rusek F, et al. Massive MIMO performance evaluation based on measured propagation data[J]. IEEE Trans on Wireless Commu, 2015, 14(7): 3899-3911. DOI:10.1109/TWC.2015.2414413 |
| [4] |
魏思菁, 周亭亭. 基于仿射传播聚类的LOS/NLOS环境识别算法[J]. 广东通信技术, 2017, 37(7): 45-50. Wei Sijing, Zhou Tingting. Affine propagation clustering based LOS/NLOS environment recognition algorithm[J]. Guangdong Communication Technology, 2017, 37(7): 45-50. DOI:10.3969/j.issn.1006-6403.2017.07.012 |
| [5] |
Xu W, Zekavat S A R. Novel high performance MIMO-OFDM based measures for NLOS identification in time-varying frequency and space selective channels[J]. IEEE Commun Lett, 2012, 16(2): 212-215. DOI:10.1109/LCOMM.2011.112311.111802 |
| [6] |
Zeng T, Chang Y, Zhang Q, et al. CNN-based LOS/NLOS identification in 3D massive MIMO systems[J]. IEEE Commun Lett, 2018, 22(12): 2491-2494. DOI:10.1109/LCOMM.2018.2872522 |
| [7] |
3GPP TS 36. 873-V12. 3. 0, Study on 3D channel model for LTE (Release 12)[S]. 2016.
|
| [8] |
Lamahewa T, Kennedy R, Abhayapala T, et al. MIMO channel correlation in general scattering environments[C]//Proc 2006 Australian Communications Theory Workshop. Australian: IEEE Press, 2006: 93-98.
|
| [9] |
Zhang J, Zheng Z, Zhang Y, et al. 3D MIMO for 5G NR:several observations from 32 to massive 256 antennas based on channel measurement[J]. IEEE Wireless Commun, 2018, 56(3): 62-70. |
| [10] |
Sadowski J. Estimation of Rician K-factor values in urban terrain[C]//2016 10th European Conference on Antennas and Propagation. Davos: Curran Associates Inc, 2016: 1-5.
|



