针对PM2.5浓度的非线性和不确定性,提出了一种基于集成树-梯度提升决策树(EnsembleTrees-GBDT)的PM2.5预测模型.该模型首先在集成树框架下进行特征选择,即选取PM2.5浓度主要影响因素,使用算术均值聚合法计算出各项特征对PM2.5浓度增加的影响程度,并以影响程度由强到弱的次序排序;其次使用网格搜索对GBDT算法进行参数优化,选取树的深度等参数的最优值;最后构建完整的PM2.5浓度集成预测模型.使用北京市2015-2016年的污染物浓度和气象条件观测值2个数据集,对模型进行了预测仿真实验.对比实验结果表明,所提出的EnsembleTrees-GBDT预测模型相比于决策树、随机森林、支持向量机等模型,具有更低的平均绝对误差和均方根误差,同时具有更好的泛化能力,能够更准确地预测PM2.5浓度,并实现对PM2.5浓度影响因素的有效分析.
The increase of PM2.5 is a cause of haze. Effectively predicting PM2.5 concentration and analyzing its influence factors play an important role in air quality forecasting and controlling. Considering nonlinearity and uncertainty of PM2.5 concentration, a PM2.5 concentration prediction model which firstly selects features using integrated trees was presented based on ensemble trees-gradient boosting decision tree(GBDT). With standard arithmetic mean aggregation method, the article calculates the influence degree of each feature on the increment of PM2.5 concentration, and provides the impact ranking from strong to weak. The grid-search to select the optimal parameters of the GBDT algorithm was used, such as the depth of the tree. Two datasets, the pollutant concentration data and meteorological observation data of Beijing from 2015 to 2016, are used in the prediction model proposed. Compared with standard models such as decision tree, random forest and support vector machine, the ensemble trees-GBDT model is found to be lower mean absolute errors, lower root mean square errors and better generalization ability.
PM2.5是指大气中直径小于或等于2.5 μm的颗粒物,也称为细颗粒物,目前已经成为大气首要污染物[1]. PM2.5粒径小,扩散面积大,易附带有毒、有害物质,是霾发生的主要因素之一[2].目前,人们在PM2.5浓度的预测上已经做了大量的工作,预测方面主要包括确定性模型和统计模型2种[3].确定性模型需要历史气象数据、化学初始条件和边界条件数据等信息来模拟污染物复杂的形成过程.此类模型预测实现需要较长的系统运行时间,同时这些数据通常难以精确获取,影响模型精度[4].随着机器学习的发展,神经网络、随机森林(RF, random forest)等模型已成功应用于PM2.5浓度预测.任才溶等[5]提出利用K-Means算法对原始气象数据聚类,然后利用欠采样方法对数据进行平衡采样,最后利用泛化能力好的RF构建预测模型.黄婕等[6]通过Stacking集成策略对递归神经网络和卷积神经网络进行融合,结合了递归神经网络的时序记忆优势和卷积神经网络的特征表达能力,并充分利用时间轴上的关联信息对PM2.5的小时浓度进行预测.在特征选择方面,张俐等[7]通过最大相关系数的方式改进快速过滤特征选择算法.崔鸿雁等[8]归纳了用于特征选择的相关性度量方法、稀疏选择方集成方法、神经网络方法和主成分分析方法,为研究者提供参考.
单一模型通常具有一定的局限性,例如,支持向量机(SVM, support vector machine)模型对缺失数据敏感;决策树(DT, decision tree)模型的结果不稳定,在数据中一个很小的变化可能导致生成一个完全不同的树;人工神经网络方法需要调整的参数过多等.为了解决这个问题,笔者提出了一种新的集成学习模型——基于集成树-梯度提升决策树(EnsembleTrees-GBDT, EnsembleTrees-gradient boosting decision tree)模型进行PM2.5的浓度预测与影响因素分析:一方面使得特征选择相关性更高、更准确;另一方面降低了模型构建中的复杂性和模型过拟合的风险.模型集成Bagging的DT、RF和极端随机树(ET, extra tree)3种算法,通过增加单个树的差异性以提高泛化性能和预测精度.由于梯度提升决策树(GBDT, gradient boosting decision tree)算法既可以处理离散值,又可以处理连续值,并且能够很好地适应异常值的鲁棒性,使得该算法适合用于解决PM2.5干扰项多和异常情况多的情况.同时,通过网格搜索(GS, grid search)对GBDT的基学习器个数、树深度等参数进行优化,提高了模型的运行效率.
1 相关研究集成学习[8]是将多个弱学习器按照一定的规则结合起来,得出性能表现优于单个弱学习器的模型.通过多年的发展,出现了很多新的思想和模型,并对多种集成学习模型进行融合.在Bagging、Boosting、AdaBoost的基础上,发展出了RF、GBDT等算法.
1.1 RF算法RF是基于Bagging算法的集成模型,一般采用分类与回归树(CART, classification and regression tree)作为基础模型,它包含多棵随机产生的DT[9].由于各DT构建过程的随机性,RF被证明不会过拟合[10],故每棵树都尽可能地生长而不需要剪枝.
1.2 ET算法Geurts等[11]提出了ET方法,根据经典的自上而下的方法,ET构建了一系列“自由生长”的回归树集合. ET方法是完全随机地得到分叉值,从而进行对回归树的分叉[12].
1.3 GBDT算法GBDT属于Boosting算法,结合了回归树与提升树的思想. GBDT与RF算法类似,但属于不同的DT模型组合方式. GBDT输出为每棵DT输出结果的累加,利用梯度提升和回归DT的组合方式,每次建立新的DT模型都是在之前模型损失函数梯度的下降方向,使得决策模型不断改进[13].
GBDT首先使用最速下降的近似方法来计算残差的近似值,即
| $ \begin{array}{*{20}{c}} {{r_{m,i}} = - {{\left[ {\frac{{\partial L\left( {{y_i},f\left( {{x_i}} \right)} \right)}}{{\partial f\left( {{x_i}} \right)}}} \right]}_{f\left( x \right) = {f_{m - 1}}\left( x \right)}},}\\ {i = 1,2, \cdots ,N} \end{array} $ | (1) |
GBDT的算法如下.
输入:训练数据集D={(x1, y1), (x2, y2), …, (xn, yn)},当损失函数为均方差时,有
| $ L\left( {y,f\left( x \right)} \right) = {\left( {y - f\left( x \right)} \right)^2} $ | (2) |
步骤1 初始化:
| $ {f_0}\left( x \right) = \mathop {\rm argmin}\limits_y \sum\limits_{i = 1}^N L \left( {{y_i},\gamma } \right) $ | (3) |
步骤2 对m=1, 2, …, M进行迭代.
步骤3 对于每一个样本(xi, yi),计算残差:
| $ {r_{im}} = - \left[ {\frac{{\partial L\left( {{y_i},f\left( {{x_i}} \right)} \right)}}{{\partial ,f\left( {{x_i}} \right)}}} \right] $ | (4) |
步骤4 利用{(xi, Rmi), i=1, 2, …, N}拟合一棵CART回归树,得出第m棵回归树Tm,其叶节点划分的区域为Rmj, j=1, 2, …, J.
步骤5 对于回归树Tm的每一个叶节点,计算其输出值:
| $ {c_{mj}} = \mathop {\rm argmin}\limits_c \sum\limits_{{x_i} \in {R_{mj}}} L \left( {{y_i},{f_{m - 1}}\left( {{x_i}} \right) + c} \right) $ | (5) |
步骤6 更新回归树:
| $ {f_m}\left( x \right) = {f_{m - 1}}\left( x \right) + \sum\limits_{j = 1}^J {{c_{mj}}} I\left( {x \in {R_{mj}}} \right) $ | (6) |
步骤7 得到最终提升回归树:
| $ \hat f\left( x \right) = {f_M}\left( x \right) + \sum\limits_{m = 1}^M {\sum\limits_{j = 1}^J {{c_{mj}}} I\left( {x \in {R_{mj}}} \right)} $ | (7) |
输出:梯度提升树
相对于DT,RF、GBDT既具有继承了DT的可解释性强,又能够很好地处理特征间的相关关系等优点,提高了泛化能力.笔者使用了DT、RF、ET等异质学习器以及GBDT算法等同质学习器.
所提出的PM2.5预测模型框架如图 1所示.在进行原始数据清洗后,使用Z-score标准化处理解决数据集中各变量单位不同、大小差异大等问题,以确保数据的可靠性与可用性.模型在EnsembleTrees框架下进行特征选择,采取算术均值聚合得出最终特征影响程度强弱排序,将其作为模型的输入变量;使用GS对GBDT算法的基学习器个数、GBDT树深度、特征个数进行优化,选出最优参数构建预测模型.

|
图 1 基于EnsembleTrees-GBDT的PM2.5预测模型框架 |
实验数据来源于国家人口与健康科学数据共享服务平台(http://www.ncmi.cn/):一部分是环保部发布的2015-01-01—2016-12-31全国省会城市空气污染指数资料,从中提取出了北京市可吸入颗粒物(PM10)、二氧化硫(SO2)、二氧化氮(NO2)、臭氧(O3)4种污染物数据;另一部分是气象条件数据,其来源于2015-01-01—2016-12-31全国700个气象站的地面气象资料,从中提取出了北京市的15项气象条件参数,如表 1所示.其中4种污染物浓度与气象条件数据构成了19维的特征数据,按日作为研究对象,即构成一个19×732的数据矩阵,表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = \left[ {{x_{11}},{x_{12}}, \cdots ,{x_{ij}}} \right],i = 1,2, \cdots ,731,}\\ {j = 1,2, \cdots ,19} \end{array} $ | (8) |
|
|
表 1 气象参数列表 |
同时将PM2.5的单日浓度作为预测目标,表示为
| $ \mathit{\boldsymbol{Y}} = \left[ {{y_{11}},{y_{12}}, \cdots ,{y_i}} \right],i = 1,2, \cdots ,731 $ | (9) |
变量采用不同单位来衡量,在用于建模之前,需进行无量纲标准化处理.根据气象因素等变量接近正态分布,选取了Z-Score算法进行标准化处理.将某个具体的观测值表示为xi,μ为观测值所在数据组的均值,σ为该组数据的标准差(见式(10)),对原始数据进行标准化,以消除不同数据水平和变量单位对结果的影响.
| $ Z\left( {{x_i}} \right) = \frac{{{x_i} - \mu }}{\sigma } $ | (10) |
特征选择的目的是对所有特征进行影响程度强弱排序,即选择出对预测PM2.5浓度影响程度较大的特征.分析特征与自变量之间的相关性,消除冗余特征和不相关特征.笔者分别使用DT、RF、ET得出特征强弱排序,再通过算术均值聚合得出最终特征强弱排序.差异性是集成学习性能优于其他算法的前提,对DT、RF、ET这3种特征选择方法的结果采用算术均值聚合,既可以保证学习器的差异性,也可以降低模型的整体误差.
特征选择的详细过程描述如下:
步骤1 计算基于DT的特征排序.
对于DT来说,假设最初总共有K类,样本属于第k类的概率为pk,则该概率分布的Gini值为
| $ {\rm{Gini}}\left( p \right) = \sum\limits_{k = 1}^K {{p_k}} \left( {1 - {p_k}} \right) = 1 - \sum\limits_{k = 1}^K {p_k^2} $ | (11) |
Gini的选择标准为:每个子节点都达到最高的纯度,此时Gini值最小,纯度最高,不确定度最小.
用平方误差最小化原则寻找树的划分点,选择最优切分点,求解
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\left( {j,s} \right)} \left[ {\mathop {\min }\limits_{c1} \sum\limits_{{x_1} \in {D_{1\left( {j,s} \right)}}} {{{\left( {{y_i} - {c_1}} \right)}^2}} + } \right.}\\ {\left. {\mathop {\min }\limits_{c2} \sum\limits_{{x_1} \in {D_{2\left( {j,s} \right)}}} {{{\left( {{y_i} - {c_2}} \right)}^2}} } \right]} \end{array} $ | (12) |
遍历每个特征的每个分割点时,使用特征A=a将D划分为D1和D2两部分,分别表示满足A=a的样本集合和不满足该条件的样本集合.式(12)中,c1、c2是D1、D2的样本均值,j为当前的样本特征,s为划分点.
确定划分点后,计算其Gini,寻找Gini系数最小特征的分割点,使得划分前和划分后的Gini系数差值最大.差值越大,则说明当前的特征对浓度的影响越大.
遍历所有特征,得出所有特征对浓度影响的强弱程度,并对其按强弱程度降序排序,最重要为1,最不重要为19,放入集合F中,记为FDT.
步骤2 计算基于RF的特征排序.
对于RF的CART而言,Gini表示为
| $ {\rm{Gini}}\left( p \right) = 2p\left( {1 - p} \right) $ | (13) |
在特征A=a的条件下,D的Gini指数为
| $ {\rm{Gini}}\left( {D,A} \right) = \frac{{\left[ {{D_1}} \right]}}{{\left| D \right|}}{\rm{Gini}}\left( {{D_1}} \right) + \frac{{\left[ {{D_2}} \right]}}{{\left| D \right|}}{\rm{Gini}}\left( {{D_2}} \right) $ | (14) |
其中:集合D的不确定性用Gini(D)表示,Gini(A, D)则表示在经过A=a分割后,集合D的不确定性.
RF中的每棵CART需要通过不断遍历这棵树的特征子集所有可能的分割点来寻找Gini系数最小特征的分割点,使得划分后的结果很纯,划分前和划分后的Gini系数差值最大.与DT的差异在于它不是在分割节点时搜索最重要的特征,而是在随机特征子集中搜索最佳特征.
遍历所有特征,得出所有特征对浓度的影响程度,并对其按影响程度大小降序排序,放入集合F中,记为FRF.
步骤3 计算基于ET的特征排序.
对于ET而言,Gini指数的计算方式与RF一致.但在寻找最佳分割点时,需先将节点的样本分成两组,对每个随机选择的特征进行随机的分割,然后选择出最佳分割.
遍历所有特征,得出所有特征对浓度的影响程度大小,并对其按影响程度大小降序排序,放入集合F中,记为FET.
步骤4 计算基于DT+RF+ET的Ensemble-Trees模型的特征影响强度值FT.
按照算术均值聚合法,计算特征Xi的平均影响程度,FT值越小,影响越强:
| $ {F_{\rm{T}}} = \left( {{F_{{\rm{DT}}}} + {F_{{\rm{RT}}}} + {F_{{\rm{ET}}}}} \right)/3 $ | (15) |
根据FT值进行升序排序.各算法特征排序结果如表 2所示.
|
|
表 2 各算法特征排序结果 |
由于GBDT算法能够很好地适应异常值的鲁棒性,并且GBDT可以同时处理离散值和连续值,使得GBDT算法适应于PM2.5数据非线性和干扰项多的情况,因此使用GBDT算法构建PM2.5浓度预测模型.
通过train_test_split函数对经过特征选择得到的特征子集Fm按照训练集70%、测试集30%的比例将其划分为训练集Ftrain和测试集Ttest.
GBDT模型在Boosting迭代框架下进行M次迭代,如式(16)所示.其中,i=0时,f(0)为初始预测值;i=1,2,…,M时,fi(x)为第i次迭代的函数增量.初始预测值和各函数增量之和即为预测值:
| $ f\left( x \right) = \sum\limits_{i = 0}^M {{f_i}\left( x \right)} $ | (16) |
GS算法将待搜索参数在一定的空间范围内划分成网格,通过遍历网格中所有的点来寻找最优参数.这种方法在寻优区间足够大且步距足够小的情况下可以找出全局最优解,但须对所有参数进行排列组合,缺点是模型搜索的时间复杂度高[14].
2.3.2 GBDT模型调参根据GS算法的思想,首先需要设置将要选择的参数组合区间.基于GBDT算法结合GS算法,进行参数优化,不断地对模型进行训练,通过评价函数对每个参数组合得到的结果进行评价,最终得到最优参数组合.该方法能够克服交叉验证的缺点,最后将最优参数组合代入GBDT算法,从而使预测性能得到提升.
笔者利用Python平台建立模型,GBDT模型需要设置基学习器个数(n-estimators)、最大特征数(max-features)以及树的深度(max-depth)3个重要参数.为防止过拟合,学习率设为0.03,对学习率设置较小的值对模型可达到正则化的效果.本研究选用的是huber损失函数来计算预测结果的残差,huber损失函数对异常值的鲁棒性非常强.基于此,对基学习器个数、分类回归树的深度以及最大特征数进行GS,最大深度设置为3~10,最大迭代次数设为50~500.
由GS结果得出,最大深度为6,最大迭代次数为200,最大特征数为9.通过集成特征选择方法选取了PM10、SO2、NO2、O3、temp_min、RH_ave、wind_max、wind_ex、sun共9项影响程度高的特征.
2.3.3 部分依赖图部分依赖(PD, partial dependence)图显示了1个或2个特征对机器学习模型的预测结果的边际效应[15]. PD图可以显示目标与特征之间的关系是线性还是非线性的,是单调还是复杂的.例如,应用于线性回归模型时,PD图总是显示线性关系.回归的PD函数定义为
| $ {f_{{x_s}}}\left( {{x_s}} \right) = {E_{{x_c}}}\left[ {f\left( {{x_s},{x_c}} \right)} \right] $ | (17) |
在模型f中,xs是PD图中绘制的特征,xc是学习模型中的其他特征.通常,集合S中只有1个或2个特征. S中的特征是对预测结果有影响的特征.特征向量xs和xc组合构成总特征空间X. PD性通过边缘化集合C中的特征分布在学习模型的输出而起作用,因此该函数显示目标集合S中的特征与预测结果之间的关系.通过边缘化其他特征,得到的函数仅依赖于S中的特征,包括该特征与其他特征的交互.
PD图展示了特征S的给定值对预测的平均边际效应. PM2.5浓度影响因素的PD图如图 2、图 3所示.

|
图 2 PM10、NO2、SO2、wind_direction_ex PD图 |
|
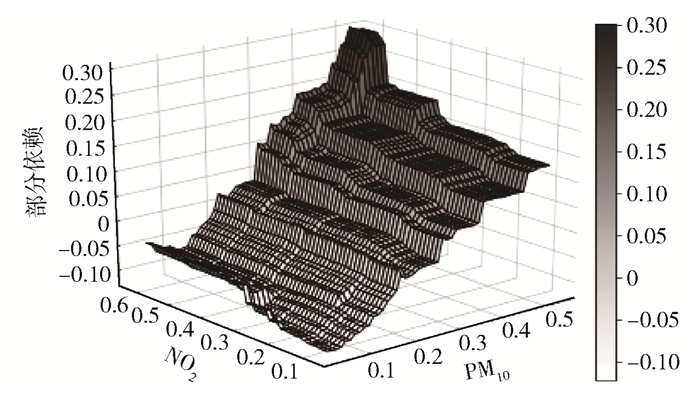
图 3 PM10与NO2联合PD图 |
图 2(a)、(b)、(c)、(d)分别为PM10浓度、NO2浓度、SO2浓度以及wind_direction_ex4个重要变量的PD图,图 2(e)为控制其他变量后的PM10与NO2的PD图,可以看出,不同变量之间存在差异效应.由于这些变量的连续性,PM10的PD函数近似阶梯函数,其他变量的PD函数近似线性函数.这4个变量的增大分别使PM2.5浓度有不同程度的上升.同时,PM10浓度也随NO2浓度增大而上升.
图 3显示了因变量与2个最重要变量(PM10浓度与NO2浓度)的联合PD图.因为它们在单个图中显示对2个变量的联合PD性,所以此图以三维呈现,显示了所涉及的变量之间不同的相互作用:PM10浓度一定,NO2依赖度高于0.5时,PM2.5浓度有明显上升;NO2浓度一定时,PM2.5浓度随PM10浓度上升而上升.
3 对比实验为了更好地验证所提出的集成模型EnsembleTrees-GBDT的有效性,设置了3组对比实验:
1) 所采用的特征选择方法与未使用该方法的结果对比;
2) 所采用的GS优化的GBDT与使用默认参数的GBDT的对比;
3) 所采用的联合模型EnsembleTrees-GBDT与使用传统DT、RF以及SVM等单一算法对比.对预测结果通过引用平均绝对误差(MAE, mean absolute errors)和均方根误差(RMSE, root mean square errors)来进行评估.
3.1 EnsembleTrees模型特征选择方法与未使用该方法的对比分析比较结果如表 3所示.可以看出,使用EnsembleTrees模型特征选择算法与未使用该方法相比,RF、DT、SVM和GS-GBDT的预测精度均有提升,更加接近真实值.
|
|
表 3 使用与未使用EnsembleTrees模型特征选择结果对比 |
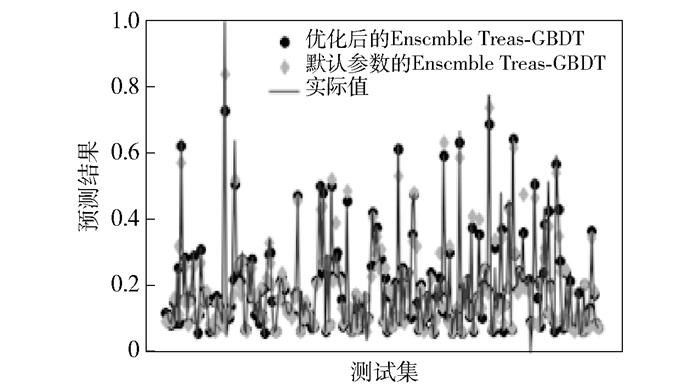
为了验证GS优化模型的有效性,将经过GS优化的GBDT与使用默认参数设置的GBDT进行对比,预测结果如图 4所示.由图 4可以看出,经过GS优化的预测结果更加接近真实值.
|
图 4 模型预测结果对比 |
表 4所示为经过参数优化的GBDT与使用默认参数GBDT预测结果的MAE和RMSE对比.由表 4可以看出,参数优化前后的MAE和RMSE都很低,说明预测结果误差较小.相对于直接使用EnsembleTrees-GBDT,GS优化之后,MAE、RMSE分别由0.031 1、0.044 8降到了0.016 4、0.033 4,模型精度更高.结果表明,GS优化后的EnsembleTrees-GBDT模型能够有效预测PM2.5的浓度.
|
|
表 4 模型结果对比 |
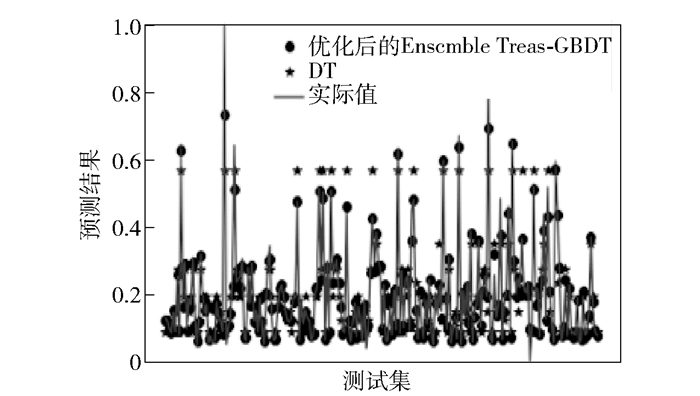
为了更好地验证所提出GS优化的集成模型EnsembleTrees-GBDT的有效性,将其与DT进行对比.预测结果如图 5所示,可以看出,相比于DT,GS优化的EnsembleTrees-GBDT的预测结果更加靠近PM2.5浓度的真实值.
|
图 5 优化后的EnsembleTrees-GBDT与DT预测结果对比 |
由表 5可以看出,相对于使用DT,GS优化的EnsembleTrees-GBDT模型的MAE、RMSE更低,误差更小,分别由0.037 0、0.060 6降到了0.016 4、0.033 4.结果表明,优化后的EnsembleTrees-GBDT模型预测精度更高.
|
|
表 5 模型结果对比 |
目前,集成学习的理论和算法研究是机器学习领域的一个热点,越来越多的集成学习方法被广泛应用于预测中.与使用单一的机器学习算法进行PM2.5预测的方法相比,笔者使用的EnsembleTrees-GBDT集成模型能够有效地分析出各影响因素对PM2.5浓度影响的大小,同时使用GS对基学习器个数、GBDT树深度、特征个数进行优化,能够有效提高模型性能与预测精度.对比实验表明,相比于单一模型,所提出的EnsembleTrees-GBDT集成模型预测误差降低、精度提升.综合实验结果表明,所提出的EnsembleTrees-GBDT集成模型可以从影响因素分析和浓度预测两方面对PM2.5污染进行分析和预测,研究工作可以为北京市PM2.5污染物的防治工作提供科学的决策依据.
| [1] |
张青, 饶灿. 典型区域城市PM2.5与PM10比值相关性研究[J]. 绿色科技, 2019(12): 129-130. Zhang Qing, Rao Can. Correlation analysis between PM2.5 and PM10 ratio in typical regional cities[J]. Journal of Green Science and Technology, 2019(12): 129-130. DOI:10.3969/j.issn.1674-9944.2019.12.049 |
| [2] |
刘晓红, 王慧. 基于中欧对比视角的货运机动车尾气排放PM2.5分析研究[J]. 环境科学学报, 2019, 39(8): 2830-2838. Liu Xiaohong, Wang Hui. An analysis of vehicle-related PM2.5 emissions:the perspective from China and Europe[J]. Acta Scientiae Circumstantiae, 2019, 39(8): 2830-2838. |
| [3] |
李建新, 刘小生, 刘静, 等. 基于MRMR-HK-SVM模型的PM2.5浓度预测[J]. 中国环境科学, 2019, 39(6): 2304-2310. Li Jianxin, Liu Xiaosheng, Liu Jing, et al. Prediction of PM2.5 concentration based on MRMR-HK-SVM model[J]. China Environmental Science, 2019, 39(6): 2304-2310. DOI:10.3969/j.issn.1000-6923.2019.06.009 |
| [4] |
王平, 张红, 秦作栋, 等. 基于wavelet-SVM的PM10浓度时序数据预测[J]. 环境科学, 2017, 38(8): 3153-3161. Wang Ping, Zhang Hong, Qin Zuodong, et al. PM10 concentration forecasting model based on wavelet-SVM[J]. Environmental Science, 2017, 38(8): 3153-3161. |
| [5] |
任才溶, 谢刚. 基于随机森林和气象参数的PM2.5浓度等级预测[J]. 计算机工程与应用, 2019, 55(2): 213-220. Ren Cairong, Xie Gang. Prediction of PM2.5 concentration level based on random forest and meteorological parameters[J]. Computer Engineering and Applications, 2019, 55(2): 213-220. |
| [6] |
黄婕, 张丰, 杜震洪, 等. 基于RNN-CNN集成深度学习模型的PM2.5小时浓度预测[J]. 浙江大学学报(理学版), 2019, 46(3): 370-379. Huang Jie, Zhang Feng, Du Zhenhong, et al. Hourly concentration prediction of PM2.5 based on RNN-CNN ensemble deep learning model[J]. Journal of Zhejiang University(Science Edition), 2019, 46(3): 370-379. |
| [7] |
张俐, 袁玉宇, 王枞. 基于最大相关信息系数的FCBF特征选择算法[J]. 北京邮电大学学报, 2018, 41(4): 86-90. Zhang Li, Yuan Yuyu, Wang Cong. FCBF feature selection algorithm based on maximum information coefficient[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(4): 86-90. |
| [8] |
崔鸿雁, 徐帅, 张利锋, 等. 机器学习中的特征选择方法研究及展望[J]. 北京邮电大学学报, 2018, 41(1): 1-12. Cui Hongyan, Xu Shuai, Zhang Lifeng, et al. The keytechniques and future vision of feature selection in machine learning[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(1): 1-12. DOI:10.3969/j.issn.1008-7729.2018.01.001 |
| [9] |
Dietterich T G. Machine learning research:four current directions[J]. AI Magazine, 1997, 18(4): 97-136. |
| [10] |
刘云翔, 陈斌, 周子宜. 一种基于随机森林的改进特征筛选算法[J]. 现代电子技术, 2019, 42(12): 117-121. Liu Yunxiang, Chen Bin, Zhou Ziyi. An improved feature selection algorithm based on random forest[J]. Modern Electronics Technique, 2019, 42(12): 117-121. |
| [11] |
Geurts P, Ernst D, Wehenkel L. Extremely randomized trees[J]. Machine Learning, 2006, 63(1): 3-42. |
| [12] |
黄丛吾, 陈报章, 马超群, 等. 基于极端随机树方法的WRF-CMAQ-MOS模型研究[J]. 气象学报, 2018, 76(5): 779-789. Huang Congwu, Chen Baozhang, Ma Chaoqun, et al. WRF-CMAQ-MOS studies based on extremely randomized trees[J]. Acta Meteorologica Sinica, 2018, 76(5): 779-789. |
| [13] |
刘金硕, 刘必为, 张密, 等. 基于GBDT的电力计量设备故障预测[J]. 计算机科学, 2019, 46(S1): 392-396. Liu Jinshuo, Liu Biwei, Zhang Mi, et al. Fault prediction of power metering equipment based on GBDT[J]. Computer Science, 2019, 46(S1): 392-396. |
| [14] |
雷雪梅, 谢依彤. 用于高血压菜谱识别的基于遗传算法的改进XGBoost模型[J]. 计算机科学, 2018, 45(增刊1): 476-481. Lei Xuemei, Xie Yitong. Improved XGBoost model based on genetic algorithm for hypertension recipe recognition[J]. Computer Science, 2018, 45(S1): 476-481. |
| [15] |
Friedman J H. Greedy function approximation:a gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. |



