2. 长鑫存储技术有限公司, 合肥 230000
提出了一种基于机器学习的多变量制造过程中的关键变量检测算法.该算法利用机器学习分类器对多变量制造过程进行数学建模,以随机打乱过程变量后分类器的性能变化作为评价指标,检测导致产品质量相对异常的关键变量.设计并生成了多变量制造过程的仿真数据集,在仿真数据集和基于中国某工厂的2个实际生产案例数据集上对算法的检测性能进行了性能验证,2次验证结果均表明算法检测性能良好.
2. Chang Xin Memory Technologies, Inc., Hefei 230000, China
A key variable detection algorithm based on machine learning in multivariate manufacturing process was proposed. It uses the machine learning classifier to mathematically model the multivariate manufacturing process. And the performance change of the classifier after the process variable shuffled randomly is used as an evaluation index to detect the key variables that lead to relatively abnormal product quality. Simulation data of the multivariate manufacturing process is designed and generated. The performance of the algorithm was verified by simulation data set and two actual production case data sets based on a factory in China. Both verifications show that the algorithm has good detection performance.
近年来, 随着技术的不断向前发展, 部分产品的制造过程变得越来越复杂, 影响最终产品质量的变量变得越来越多.在这种多变量制造过程[1]中, 任何一个过程变量出现异常都会导致最终生产得到的产品质量相对异常.为了提高产品的质量, 增强企业的核心竞争力, 对产品的多变量制造过程进行监控和分析是必不可少的.
统计过程控制(SPC, statistical process control)技术如质量控制图通常被用于监控产品的生产状态[2]. SPC可以对多变量制造过程中的每个变量数据进行实时监控, 判断其是否处于受控状态.当某变量明显偏离设定值时, 质量控制图判断其处于不受控状态, 便会立即发出警报, 提醒工程师进行修正.
在多变量制造过程中, 即使所有变量均处于受控状态, 产品仍会出现质量相对异常的现象.这种质量异常可能是由于某过程变量的细微扰动或者多个过程变量综合影响所导致.此时, 需要从庞大的过程变量数据中精确定位到导致产品质量相对异常的关键过程变量, 从而帮助工程师迅速解决问题,使得制程恢复正常.传统的质量控制图技术无法从庞大的变量数据中精确地检测出导致产品质量相对异常的关键过程变量[3].为了解决此问题, 近年来机器学习技术被广泛应用于从复杂的多变量制造过程数据中提取有用信息, 检测出导致产品质量相对异常的关键过程变量.
早在2000年就有学者提出利用自组织映射网络和规则归纳来对半导体制造过程中导致最终样片质量相对异常的关键过程变量进行检测, 并在摩托罗拉半导体部门的实际生产数据中进行了算法实际性能验证, 算法检测结果与工程师经多次实际实验检测出的结果相一致[4].但该研究仅针对半导体制造过程中的少数变量进行了分析, 没有考察全部的过程变量.
之后陆续有诸多学者就此问题展开深入研究. Karimi等[5]在2014提出利用多个人工神经网络(ANN, artificial neural network)模型进行集成学习来检测多变量制造过程中的关键过程变量, 然而该研究实际上主要分析的是多变量控制图失控的关键变量, 仅对特定的多变量控制图涉及的变量进行了分析.同样在2014年, Chien等[6]提出利用Kruskal-Wallis检验和方差分析(ANOVA, analysis of variance)来进行关键变量检测, 但该研究未对其所用说明其实际性能验证时所用数据, 说服力不足.在2017年, Chien等[7]又提出采用逻辑回归(LR, logistics regression)模型和随机森林(RF, random forest)模型相结合来进行关键过程变量的检测.该算法可以精确检测出仅有单个关键变量的问题, 但无法检测出包含多个关键变量的问题. Chen等[8]于2017年给出基于lasso回归和RF模型的关键过程变量检测算法, 其提出一个两阶段的关键变量检测算法, 但在初始阶段检测时仅对产品是否通过机台的0/1数据进行了分析, 没有对实际过程变量进行分析.而Marzieh Khakifirooz等[9]则于2018年提出通过贝叶斯推断来检测关键的过程变量.但该算法在实际数据集中的检测结果仅从数据层面分析了其可能为关键的过程变量, 未能经过实际确认.
目前现有的研究都是利用特定的机器学习模型的一些特性来进行关键变量的检测, 不同情况下的数据集对不同模型的拟合程度有所不同, 单一的机器学习模型难以适用于所有情况.提出了一种基于机器学习分类器的关键过程变量检测算法.该算法不仅仅考察某个特定的机器学习模型, 而是对多变量制造过程本身进行分析.在本算法中, 分类模型仅仅用于对多变量制造过程进行建模拟合.针对不同的数据集可以选择拟合效果最好的模型来分析.
为了验证所提算法的检测性能, 设计并生成了仿真数据, 在仿真数据上进行了算法性能测试.而后基于中国某芯片工厂的实际产品数据, 对笔者所提算法的检测性能进行了实际数据验证.
1 关键变量检测算法 1.1 问题定义假设多变量制造过程中存在n个变量对最终产品的性能存在影响, n个变量分别为f1, f2, …, fn,其中变量fk1, fk2, …, fkj在制造过程中出现异常, 导致部分产品质量相对异常.质量相对正常的产品标记为“1”, 质量相对异常的产品标记为“0”.笔者所研究的问题即为检测出导致产品质量相对异常的关键过程变量fk1, fk2, …, fkj.
上述研究问题可转换为如下数学模型:
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\left( {{f_{{k_1}}}, {f_{{k_2}}}, \cdots , {f_{{k_j}}}} \right)} h\left( {{f_{{k_1}}}, {f_{{k_2}}}, \cdots , {f_{{k_j}}}, y} \right)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\left( {{f_1}, {f_2}, \cdots , {f_n}} \right) \to y}\\ {\left( {{f_{{k_1}}}, {f_{{k_2}}}, \cdots , {f_{{k_j}}}} \right) \subseteq \left( {{f_1}, {f_2}, \cdots , {f_n}} \right)} \end{array} $ | (1) |
其中h(fk1, fk2, …, fkj, y)为变量子集(fk1, fk2, …, fkj)对y(label数据)划分的贡献.在实际问题中, 过程变量子集(fk1, fk2, …, fkj)的取值空间过于庞大, 难以直接求解, 考虑将问题(1)简化为问题(2)进行求解.
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\left( {{f_k}} \right)} \;h\left( {{f_k}, y} \right)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\left( {{f_1}, {f_2}, \cdots , {f_n}} \right) \to y}\\ {{f_k} \subseteq \left( {{f_1}, {f_2}, \cdots , {f_n}} \right)} \end{array} $ | (2) |
所提算法将针对问题(2)给出排名前l′(l′的取值由工程师的实际需求而定)的过程变量, 再交给工程师, 通过他们的专业知识和实际生产过程中的一些测试来检测实际的关键过程变量.
1.2 乱序操作乱序指的是将数组元素的排列顺序随机打乱.乱序操作有着多种实现方式, 本研究基于如下所示算法实现对过程变量数据fi的乱序操作.
输入:过程变量数据fi;
数据集中产品数据量m;
过程:
1 for i=1:m do
2 p←random integer with 0≤p≤m-i;
3 fi[p]↔fi[m-i];
4 end for
5 return fi;
输出:乱序后的过程变量fi.
在对过程变量fi进行乱序操作后, fi中的数据排列顺序发生变化, fi中数据与产品中的其他变量数据和产品label数据不再对应.
1.3 检测原理所提算法主要是利用机器学习分类算法对多变量制造过程进行数学建模, 而后对每个过程变量数据进行乱序, 通过乱序后分类模型的分类性能变化来检测导致产品质量异常的关键过程变量.
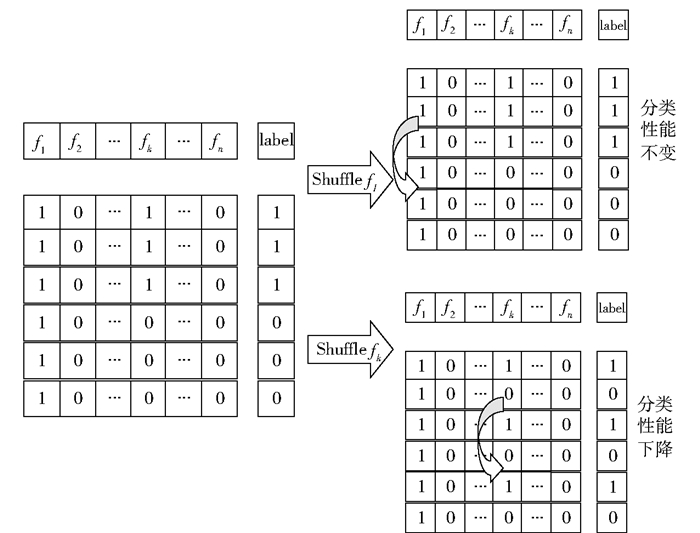
算法的检测原理如图 1所示.由于正常变量与最终label的生成无关, label数据仅由关键变量数据生成.为了便于说明, 有如下5个假设:
|
图 1 算法检测原理图 |
1) 正常变量在所有的产品上数值相同;
2) 关键变量fk在对应“0”和“1”两类label时数据为简单的0/1;
3) 分类器的分类性能已得到最优;
4) 仅有一个关键变量fk;
5) label为“0”和“1”的数据比例相同.
从图 1可以看出, 当对正常变量f1进行乱序后, 分类器的分类性能未发生改变, 而在对关键变量fk进行乱序后, 分类器的分类性能出现明显下降.
1.4 算法描述针对多变量制造过程中的关键变量检测问题, 所提关键变量检测算法如下.
输入:数据集(f1, f2, …, fn, y);
分类器clf;
可疑关键变量选取阈值l′;
过程:
1 依据数据集训练分类器clf;
2 计算clf对数据集(f1, f2, …, fn, y)分类精确度a;
3 for i=1, 2, …, n do:
4 对变量fi进行随机打乱得到f′i;
5 计算clf对(f1, …, f′i, …, fn, y)的分类精确度ai;
6 求得变量fi的可疑评分为a-ai;
7 end for
8 return评分最高的l′个变量;
输出:l′个可疑的关键变量.
1.5 评价指标以查准率P和查全率R来衡量算法的检测性能.将过程变量根据其真实类别与检测结果的组合划分为真正例(TP,true positive)nTP、假正例(FP, false positive)nFP、真反例(TN,ture negative)nTN、假反例(FN, false negative)nFN四种情形.检测结果的混淆矩阵如表 1所示.
|
|
表 1 检测结果的混淆矩阵 |
查准率P和查全率R的定义如下:
| $ \left. {\begin{array}{*{20}{l}} {P = \frac{{{n_{{\rm{TP}}}}}}{{{n_{{\rm{TP}}}} + {n_{{\rm{FP}}}}}}}\\ {R = \frac{{{n_{{\rm{TP}}}}}}{{{n_{{\rm{TP}}}} + {n_{{\rm{FN}}}}}}} \end{array}} \right\} $ | (3) |
查准率P表示算法检测出的关键变量中真实的关键变量所占比例, 而查全率表示被检测出来的真实关键变量在全部真实关键变量中所占的比例.查准率和查全率是一对相矛盾的性能指标.一般来说, 查准率高时, 查全率往往偏低;而查全率高时, 查准率往往偏低.
2 基于仿真数据的性能验证 2.1 仿真数据生成在实际多变量制造过程中, 不同批次的产品的过程变量一般都是在其工艺设定值上下波动, 其分布近似于高斯分布.对于导致最终产品质量异常的关键变量, 通常都是由于其值高于/低于工艺设定值而导致, 考虑通过对正常变量加上0/1二项分布的噪声来得到.为了生成符合实际多变量制造过程的仿真数据, 基于以下规则生成仿真数据.
1) 多变量制造过程中正常过程变量仿真数据fi~N(μi, σi)(i=1, 2, …, n), 其中N(μi, σi)表示均值为μi, 方差为σi的高斯分布;
2) μ=(μ1, …, μn)~U[a1, b1], U[a1, b1]表示[a1, b1]范围的均匀分布;
3) σ=(σ1, …, σn)~U[a2, b2], U[a2, b2]表示[a2, b2]范围的均匀分布;
4) 关键变量fkj=N(μkj, σkj)+nkj(j=1, 2, …, l), 其中噪声nkj~B(m, 0.5), B(m, 0.5)表示概率为0.5, 共发生m次的二项分布, m为仿真数据集中产品数量.
5) 仿真数据中第t件产品的label为
| $ {y_t} = \left\{ {\begin{array}{*{20}{l}} {1, }&{{\rm{ if }}\sum\limits_{j = 1}^l {n_{{k_j}}^t} < t}\\ {0, }&{{\rm{ if }}\sum\limits_{j = 1}^l {n_{{k_j}}^t} \ge t} \end{array}} \right. $ |
其中t表示仿真数据集表示的多变量制造过程中过程变量对噪声总的容忍度阈值.
考虑到数据集变量的均值对算法检测性能不会有太大影响.固定参数(a1, b1, a2)=(0, 80, 0), 给参数集(b2, m, l)分别设定不同的值, 其中仿真数据集中产品数量m分别为300、600、900, 关键变量的数量l为1、2、3、4、5, 数据集变量方差的变化范围b2为0.4、0.8、1.2、1.6、2.0、2.8, 并针对每种参数组合分别随机选取多组变量作为关键变量, 生成了多组仿真数据.而后基于生成的仿真数据集对笔者所提算法的检测性能进行了验证.
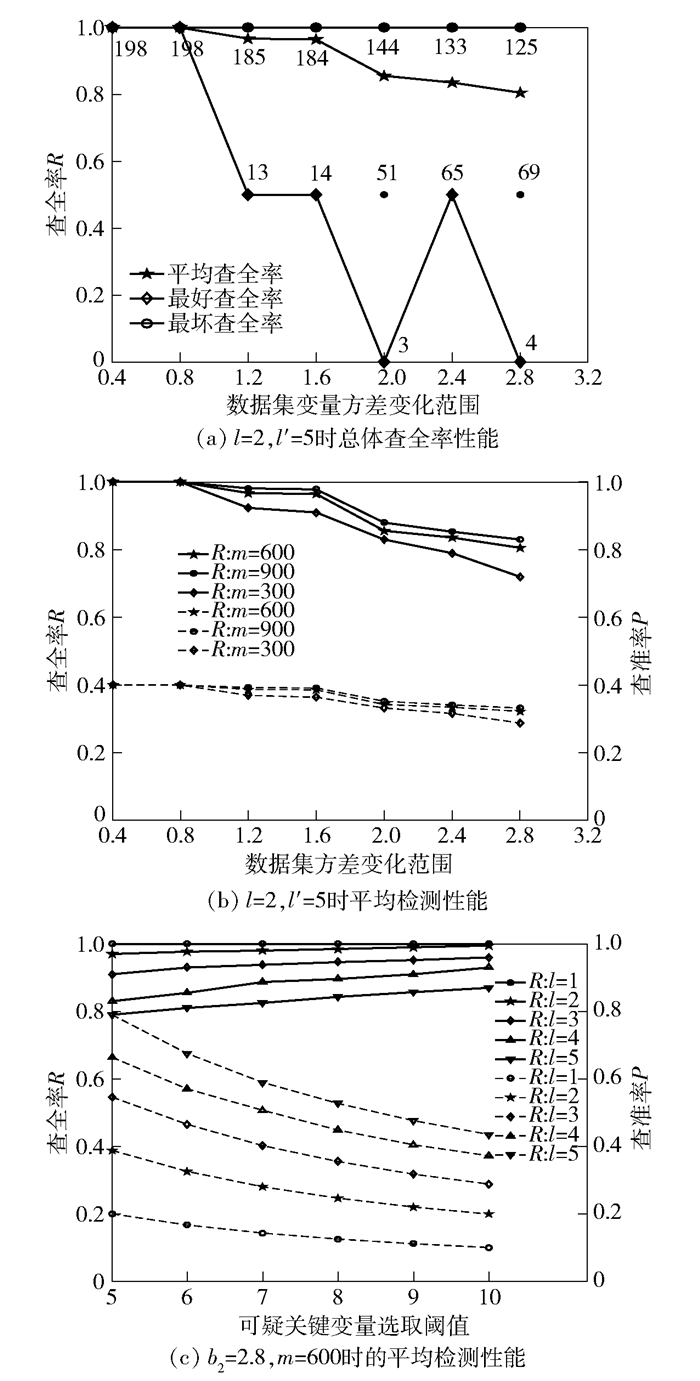
2.2 算法性能分析在仿真数据集的算法验证中, 采用了人工神经网络对仿真的多变量制造过程进行建模.在不同参数条件下的仿真数据集中, 所提算法表现出不同的检测性能. 图 2(a)所示为在关键变量数l=2, 可能关键变量选取阈值l′=5, 产品数量m=600的情况下算法的总体查全率性能.
|
图 2 仿真数据算法检测性能 |
图中的每个点都表示算法在某个仿真数据集中的检测结果, 对于重合的点用数字表明其数量. 图 2(b)所示为在l=2, l′=5的条件下, 算法在不同的数据集变量方差变化范围以及不同产品数量情况下的平均查准率和查全率性能曲线. 图 2(c)所示为产品数量m=600, 数据集方差变化范围b2=2.8时, 算法在不同的关键变量数以及不同的可能关键变量选取阈值情况下的平均查准率和查全率性能曲线.
从图 2(a)可以看出, 所提算法在仿真数据集上最好,查全率始终为100%, 且绝大多数检测结果都能达到最好的性能, 而随着数据集变量方差的增大, 仅有少部分数据集未达到最好检测性能, 平均查全率始终在80%以上. 图 2(b)表明, 随着数据集中产品数量的增大, 算法的检测性能呈上升趋势, 而随着数据集变量方差的增大, 关键变量中添加的干扰对数据本身的影响变小, 算法的检测性能下降. 图 2(c)说明, 当数据集中关键变量的数据增加, 算法的查全率性能下降, 查准率性能上升;而随着可能关键变量判断阈值的增大, 算法的查全率性能上升, 查准率性能下降.
为了进一步验证所提检测算法的性能, 基于仿真数据集, 针对所提算法与以下3种现有的关键变量检测算法, 进行了相关仿真对比实验, 并就算法检测性能进行了比对分析.
1) 基于ANOVA Test的检测算法[6].
2) 基于LR的检测算法[7].
3) 基于RF的检测算法[8].
其中基于ANOVA Test的检测算法主要通过对变量和label进行方差分析来决定, 而基于LR的检测算法和基于RF的检测算法都是基于其模型本身的可解释性来决定的.通过仿真实验发现,当将LR/RF模型分别作为所提算法中的数据建模分类模型时, 所提算法的检测性能与基于LR/RF检测算法的检测性能几乎完全一致.
目前现有的检测算法都是利用特定机器学习模型的一些特性进行关键变量的检测.而笔者所提算法则是一种普适的, 可自由选择分类模型的检测算法.为了进一步进行检测算法的性能比对, 从ANN/LR/RF等多个分类器中选择分类性能最好的作为所提算法的数据建模模型, 并与3种现有的检测算法进行性能比对, 仿真结果如图 3所示.

|
图 3 不同算法平均检测性能 |
图 3所示为m=600, l=2, l′=5的情况下, 所提算法和上述3种现有检测算法在多个不同仿真数据集中的平均检测性能.
从图 3可以看出, 在仿真数据集方差变化范围小于1.2时, 所提算法和现有的关键变量检测算法均能达到100%的查全率, 而随着数据集方差变化范围的增大, 算法平均检测性能均有不同程度的下降, 所提算法在不同仿真数据集上的平均查准查全率要略高于现有的一些关键检测算法.相比于现有的关键变量检测算法, 所提算法的普适性更强.
3 基于真实数据的性能验证半导体制造过程复杂, 影响变量繁多, 从原材料硅片到最终的样片要经过数百道operation, 是一个典型的多变量制造过程.为了进一步验证所提算法的检测性能, 基于中国某工厂的2个实际案例数据, 对算法检测性能进行了实例验证.
3.1 数据准备半导体制造过程中, 为了实时监控机台的运行状态, 各个机台都安装有大量的传感器.这些传感器数据直接表明每个机台运行时的一些物理性质, 如温度、压力、气体的流速等.在算法的实际性能验真中, 这些传感器数据即为半导体制造过程中的变量数据.为了便于分析, 将传感器数据拆分为不同的阶段, 用每个阶段的一些统计特性来表示.以operation1中的温度数据为例, 其时间序列数据可以分为3个阶段, 分别用3个过程变量(operation1-temp-step1, operation1-temp-step2, operation1-temp-step3)来表示.样片在加工完成后会通过一系列的性能测试, 根据测试结果, 可以对晶圆进行分类, 质量相对异常的样片被标记为“0”, 质量相对正常的样片被标记为“1”.这即为半导体制造过程中产品的label数据.
案例 1 数据集为该工厂的某批样片数据, 共361个样片的传感器数据和label数据, 其中label为“0”的样片共121个, label为“1”的样片共240个.在对数据进行一些格式转换和预处理操作后, 数据集包含14 847个过程变量.
案例 2 数据集为该工厂的另一批样片数据, 共250个样片的传感器数据和label数据, 其中label为“0”的样片共76个, label为“1”的样片共174个.在对数据进行一些格式转换和预处理操作后, 数据集包含13 939个变量.
3.2 算法改进在基于半导体制造过程中的实际数据进行算法性能验证时, 由于数据集过程变量达到上万个, 而对应的样片数据仅有几百片, 分类器难以直接对整个制造过程进行建模.为了解决这一问题, 依据半导体生产过程中的operation信息, 将原始数据集划分为不同的数据子集, 每个数据子集仅包含单个operation中的全部过程变量数据.而后对每个operation对应的数据子集分别运行所提算法.
同时为了识别实际关键变量位于哪些operation中, 在用分类器对每个operation对应的制造过程进行建模分析时, 将operationk对应的数据子集训练好的分类器分类精确度ak作为operationk的可疑性评分, 其中k=1, 2, …, K, K为半导体制造过程中样片经过的operation数量. ak越高, 关键变量越可能位于operationk对应的数据子集中.
最后依据工厂工程师的建议, 检测算法最终从全部operation的检测结果中选择分类精确度最高的10个operation以及其各自排名前5的过程变量作为可疑的关键过程变量交由工程师去验证.
3.3 改进算法性能分析经由工厂工程师确认, 2个实际案例的关键过程变量均在所提算法的检测结果中.

|
图 4 实际案例关键变量检测结果 |
图 4所示为2个案例中评分排名前10的operation和其中关键operation中变量评分排名前5的过程变量.从图 4可以看出, 所提算法在基于实际生产数据的性能验证中表现良好.在2个实际案例中, 算法均成功检测出实际的关键变量, 查全率都达到了100%.在案例1和案例2中, 针对整个半导体制造过程算法查准率仅为2%和4%, 但对于关键变量所在的operation, 算法的查准率分别达到20%和40%, 且关键过程变量的评分明显高于正常变量.
4 结束语针对多变量制造过程中导致产品质量相对异常的关键变量检测问题, 提出了一种基于机器学习的检测算法.该算法通过利用机器学习分类器对多变量制造过程进行建模, 而后以过程变量随机打乱后分类器的性能变化作为评价指标, 检测导致产品质量异常的关键变量.在仿真数据集和基于中国某芯片工厂的2个实际案例数据检测中,算法呈现出良好的检测性能.
| [1] |
Yeh A B, Chen H. A nonparametric multivariate process capability index[J]. International Journal of Modelling and Simulation, 2001, 21(3): 218-223. DOI:10.1080/02286203.2001.11442205 |
| [2] |
贾新章, 游海龙, 顾铠. 统计过程控制理论与实践[M]. 北京: 电子工业出版社, 2017.
|
| [3] |
Diren D D, Boran S, Selvi I H, et al. Root cause detection with an ensemble machine learning approach in the multivariate manufacturing process[M]. Cham: Springer International Publishing, 2019: 163-174.
|
| [4] |
Gardner M, Bieker J. Data mining solves tough semiconductor manufacturing problems[C]//Proceedings of the sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining-KDD'00. New York: ACM Press, 2000: 376-383.
|
| [5] |
Karimi P, Jazayeri R. Comparing the fault diagnosis performances of single neural network and two ensemble neural networks based on the boosting methods[J]. Journal of Automation and Control, 2014, 2(1): 21-32. |
| [6] |
Chien Chenfu, Chang Kuohao, Wang W C. An empirical study of design-of-experiment data mining for yield-loss diagnosis for semiconductor manufacturing[J]. Journal of Intelligent Manufacturing, 2014, 25(5): 961-972. DOI:10.1007/s10845-013-0791-5 |
| [7] |
Chien Chenfu, Liu C W, Chuang S C. Analysing semiconductor manufacturing big data for root cause detection of excursion for yield enhancement[J]. International Journal of Production Research, 2017, 55(17): 5095-5107. DOI:10.1080/00207543.2015.1109153 |
| [8] |
Chen Y J, Wang Bocheng, Wu J Z, et al. Big data analytic for multivariate fault detection and classification in semiconductor manufacturing[C]//2017 13th IEEE Conference on Automation Science and Engineering (CASE). New York: IEEE Press, 2017: 731-736.
|
| [9] |
Khakifirooz Marzieh, Chien Chenfu, Chen Yingjen. Bayesian inference for mining semiconductor manufacturing big data for yield enhancement and smart production to empower industry 4.0[J]. Applied Soft Computing, 2018(68): 990-999. |


