2. 中国航天空气动力技术研究院, 北京 100074
传统的流线可视化方法因视线遮挡和数据密集难以刻画流场特征,难以应对大规模数据,为此,从数据驱动的思路出发,提出了一种筛选三维流线的算法,实现对大规模精细流场的特征刻画.该算法对广泛撒点取得的流线集进行特征化,通过计算流线上各点的特征,并以此为依据对流线进行分段;基于所有分段的几何特征构建一组特征向量,并利用词袋方法建立一组词向量;以词向量为基础计算流线间的几何特征相似度,以评估各个流线间的相似性,实现对流线的筛选.通过在特定流线的查询和整体流线流场的压缩这2个典型应用场景上的应用,检验了该方法对流线筛选的效果.
2. China Academy of Aerospace Aerodynamics, Beijing 100074, China
With the wide application of fluid mechanics, more and more large-scale fine flow fields have emerged. Overlapping streamlines and dense fields make it hard to use the traditional streamline visualization methods to characterizes the flow fields or process with large-scale fine flow fields. Based on the idea of data-driven, this paper presents an algorithm to implement the characterization of large-scale fine flow fields. The algorithm characterizes streamlines obtained by widely spreading seed points, calculates the features of each point, segments the streamlines based on the features, and then constructs a set of feature vectors and a set of word vectors. Then, the algorithm calculates the geometric feature similarity between streamlines to evaluate streamline similarity and achieves streamlines filtering. Two typical application scenarios, streamline query and flow field compression, verify the proposed method.
三维流场数据被广泛应用于气象、航空航天等科学计算及工程应用领域,其具有较大的规模和精细的结构.流线是流场数据的直观表现,分析人员借助流场可视化直观地观察流场.基于流线的几何可视化方法在各类流场可视化场景得到了广泛的应用.
基于流线的可视化方法使用[1] “撒点—追踪—可视化”三步走策略,先在流场中选取若干种子点作为流线追踪的起点,再使用流线追踪算法获取流线,最后在流场空间中绘制出每条流线,既能展示每条流线的数据,又能展现流场随时间的变化.随着计算机模拟技术的发展,流场的规模不断攀升,其精细化程度亦稳步提高.对于大规模精细流场数据,若选取的种子点过于稀疏,则追踪所得的流线往往不足以完整描述流场的细节;若撒点过于密集,则生成的流线过多,可能引发流线重叠、流线遮挡等问题,前者引入了冗余的流线信息,后者对分析人员造成了干扰,二者均降低了流场图像的质量.
为了得到清晰、精确的流场图像,可以引入数据驱动的概念,通过广泛撒点、对追踪所得的流线进行特征化处理,并量化流线间关系,实现流线的查询和流场的压缩.基于流线上各点的特征,对流线进行分段,再引入嵌入算法,将分段嵌入成词向量.基于词向量在空间中的距离刻画流线间的距离,基于特征考虑流线内各点、各分段间的相互关系.本算法结合流线的空间位置关系和流线内各个分段的距离,将流场嵌入至特征词向量,借此提高后续任务的性能.
所述算法是一种新颖的流线特征化筛选算法,基于流线的几何特征将流线分为若干段单一特征的流线分段,基于流线上各点的特征值将流线分段嵌入至分段特征向量,使用主成分分析方法对分段特征向量进行降维,并使用K均值算法对降维后的分段特征向量进行聚类.算法引入词袋模型,将流线上各对分段视为表达式,基于各表达式的空间特性对其赋权,将各表达式加权累加以计算流线的特征词向量.算法基于TF-IDF算法对各表达式赋权,并以此权重计算流线间的相似度.最后,算法引入贪心法,计算流场内的主要流线以压缩流场,改善流场可视化的效果.
1 相关研究早期研究着重于选取种子点.为了描述撒点策略,Ye等[2]引入撒点模板以表述目标周围种子点的分布.关键点的位置显著影响流场的特征,其基于关键点间的位置关系使用不同的撒点模板来优化图像. Edmunds[3]对流场中的向量进行聚类,分析各点流向的结构,据此建立撒点模板.郭雨蒙等[4]提出了流线相似度引导种子点分布的并行处理方法. Marchesin等[5]使用流线的几何特征指定流线分布.李春鑫等[6]引入基于支持向量机的预处理模型来控制流线的疏密.然而,这样的策略要求撒点前掌握流场的特征,不适用于精细流场. Li等[7]引入人工输入来区分主次流线.流线可能经过具有不同特性的区域,故引入分割点的概念,将不同特性的流线切分成两段分段.用户指出分割点作为正样本,使用支持向量机等学习用户分类,从而有监督地分类流线分段,最后获取完整流线的特性. Yu等[8]建立流线集合的层次化结构,在不同尺度下选择流线,基于流线间的位置关系自底向上地建立层次化的流线间结构.
借此,引入数据驱动的概念,通过广泛撒点获取大量流线数据,用有监督或无监督的策略学习流线的特征,从而建立流线间的关系网络,进而对流线进行筛选、获取高质量的流场图像.此类算法通过计算流线对上各点的空间关系,如最短距离、最长距离、平均距离或狗绳距离等距离评估流线对的相似度.
基于流线的几何特征可以得出流线间的相似度. Rossl等[9]提出将流线转化为向量,计算向量间的相似度,来计算流线间的相似度. Liu等[10]考虑流线的子结构,将流线视为子结构的集合,将子结构视为字符,流线即为字符串,计算字符串间的相似度即可得到流线间的相似度. Li等[11]引入词袋模型来计算流线间的相似度. Han等[12]基于卷积神经网络实现流场数据的压缩. Wang等[13]提出基于输入的流线搜索方法. Li等[14]基于点的特征向量,采用词袋模型建立流线的特征向量.
为了提高计算速度,Tang等[15]引入并行计算来加速计算.其在三维流线相似度模型下,并行撒点,计算相似度,提高了整体计算效率.
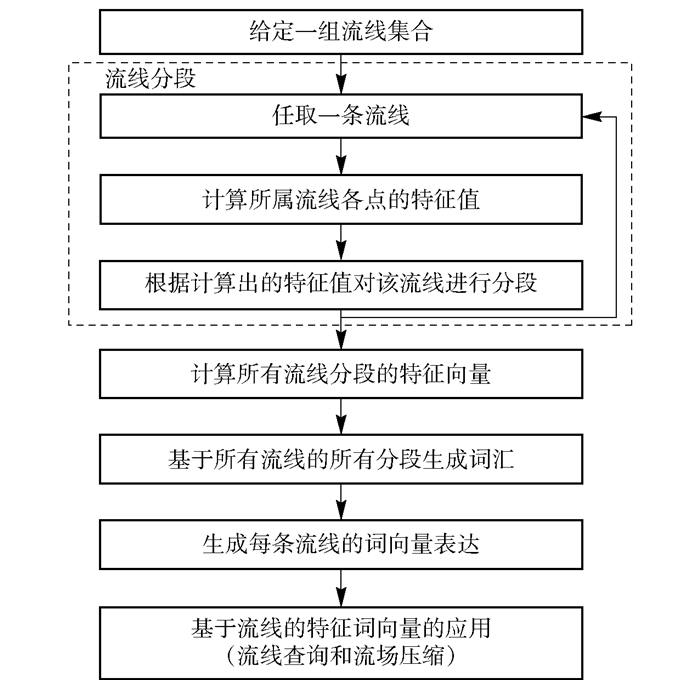
深度学习技术亦对流线表示、查询和流场压缩有所帮助. Han等[16]通过两阶段深度学习方法实现流场的压缩.其对各点的速度进行插值后,建立低分辨率的流场,再模仿图片超分辨率算法,用卷积神经网络重建高分辨率流场. Han等[17]提出基于自动编码器的流线特征提取模型,其FlowNet框架使用自动编码器获取流线低维特征向量,据此计算流线间相似度. 图 1所示为后续流程的整体框图,其中虚线框内的最后一步见2.1节.
|
图 1 数据驱动的三维流场流线特征化筛选方法 |
使用4个特征描述流场中的流线和流线上的点.对于每一个特征,计算各点的特征值,进而计算该特征的特征向量,最后将各个特征的向量与流线的规模向量相连,得到流线的特征向量.
曲率描述流线的弯曲程度.记x′、y′为x和y的一阶导数,x″、y″为x和y的二阶导数,有
| $ \mathit{\boldsymbol{\kappa }} = \frac{{\left| {{x^\prime }(t){y^{\prime \prime }}(t) - {x^{\prime \prime }}(t){y^\prime }(t)} \right|}}{{{{\left( {{x^{\prime 2(t)}} + {y^{\prime 2(t)}}} \right)}^{\frac{3}{2}}}}} $ | (1) |
挠率描述了空间曲线远离平面的程度.记x′、y′为x和y的一阶导数,x″、y″为x和y的二阶导数,x"'、y"'为x和y的三阶导数.计算公式如下:
| $ t = \frac{{{x^{\prime \prime \prime }}\left( {{y^\prime }{z^{\prime \prime }} - {y^{\prime \prime }}{z^\prime }} \right) + {y^{\prime \prime \prime }}\left( {{x^{\prime \prime }}{z^\prime } - {x^\prime }{z^{\prime \prime }}} \right) + {z^{\prime \prime \prime }}\left( {{x^\prime }{y^{\prime \prime }} - {x^{\prime \prime }}{y^\prime }} \right)}}{{{{\left( {{y^\prime }{z^{\prime \prime }} - {y^{\prime \prime }}{z^\prime }} \right)}^2} + {{\left( {{x^{\prime \prime }}{z^\prime } - {x^\prime }{z^{\prime \prime }}} \right)}^2} + {{\left( {{x^\prime }{y^{\prime \prime }} - {x^{\prime \prime }}{y^\prime }} \right)}^2}}} $ | (2) |
曲折度描述曲线偏离直线的程度,其中l为流线的长度,S和E分别为流线的起始端点和终止端点的坐标,故‖S-E‖为其直线距离.有
| $ t = \frac{l}{{\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{E}}} \right\|}} $ | (3) |
速度方向熵表征流线方向的变化.在空间球坐标系中,流线速度的方向为一单位向量,其与单位球上的点一一对应.将单位球分成M个面积相等的曲面,则每个方向映射到一个曲面.为曲面编号,则速度方向可用编号表示,流线速度方向可用正整数序列表示,该序列的熵为流线速度方向熵.序列中的各个正整数为信号,记pi为各采样值的频率,则有
| $ e = - \sum\limits_{i = 1}^M {{p_i}} \log \left( {{p_i}} \right) $ | (4) |
平直流线的特征弱,而曲折流线具有显著的特性,其特征与曲率的变化关系紧密,故基于曲率进行分段.该方法关注流线上曲率较大、变化率较大的位置,如受流场影响而剧烈弯曲的部分及其邻域.
曲率较大,且为曲率极值点的点,即潜在的分段中点.将流线的端点加入潜在的分段中点序列,遍历各个潜在的分段中点.以其曲率加权,计算相邻潜在的分段中点间的加权中点,即为潜在的分段点.
设a和b为一对相邻潜在的分段中点,d(a)和d(b)分别为其距流线起始端点的距离,且d(a) < d(b),则对应潜在分段点距流线起点的距离d(sab)为
| $ \begin{array}{l} d\left( {{s_{ab}}} \right) = d(a) + (d(b) - d(a))\alpha + (d(b) - d(a)) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1 - \alpha )\frac{{C(a)}}{{C(a) + C(b)}} \end{array} $ | (5) |
其中α为一个0~1的常数,描述允许被用于分段的距离占相邻潜在分段中点距离的比重.
基于曲率的变化率计算潜在的分段点,将二者所得的潜在的分段点序列合并,得到最终的序列.
将流线的起终点加入最终的潜在分段点序列,并从流线的起点开始遍历序列.以流线的起点为初始分段起点s,以序列中的第2个点为初始分段终点e,遍历各点,若分段起点与分段终点间的距离d(e)-d(s)大于最小分段长度阈值,则将分段(s, e)插入序列,并依次将分段起点s设为该分段终点e,再将分段终点e设为新的分段起点s的后一个潜在的分段点,直至遍历完所有潜在的分段点.若遍历至流线终止端点时,当前分段的长度d(e)-d(s)依然小于最小分段长度阈值,则将其与分段序列中的最后一个分段合并.
2.2 计算流线分段的特征向量引入金字塔模型以计算流线分段的特征向量.将各分段上各特征点的特征值自流线起始端点方向至流线终止端点方向排列,形成分段的几何特征向量(x1, x2, …, xl).将该几何特征向量作为底层,依照规则
自上至下,自左至右依次选取N个元素,将其顺序排列,形成对应分段的几何特征向量(x′1, x′2, …, x′N).依次计算各个特征的几何特征向量,并计算分段的规模特征向量(l, ld),将其连接,形成分段的特征向量.
2.3 基于流线分段生成词汇基于词袋模型,使用词汇表示流线中各分段的特征向量,进而表现流线的特征. Li等[14]提出了基于点的特征向量建立流线的词袋模型,但其使用的点的特征数较少,故其词袋模型的词汇数量相对有限,降低了模型的性能.而所述模型基于流线分段建立词袋模型,故词汇更多,性能亦更高.
将上述流线分段的特征向量分别映射至一个词汇,引入聚类映射.考虑到流线分段的特征向量维度较高,常见的聚类算法难以对其准确聚类,在聚类前先对流线分段的特征向量执行主成分分析,将其降维至K维低维空间,再进一步聚类.将K维特征向量使用K-Means聚集到V个聚类中心上.
2.4 生成流线的词向量表达引入与每个词汇一一对应的独热向量,其长度即为词汇集合的大小V.取定V=32,采用算法1计算流线的词向量表达.
算法 1 计算流线的词向量表达
S:=0 //初始化流线维特征词向量为零向量
For streamline s in dataset:
For segment a in streamline:
θa:=流线分段a的独热向量
For segment b in streamline:
If a!=b:
θb:=流线分段a的独热向量
ei=θa×θbT //表达式i的特征词向量
S:=S+wiei //加权累加表达式的特征词向量
对每一个流线分段,使用其词汇对应的独热向量θ表示其特征.对于每条流线,计算其空间敏感的词袋特征词向量B.在该模型下,将流线上的一对分段称为一个表达式,考虑到本模型中共有V个不同的词汇,每个表达式均对应2个流线分段,即2个词汇,故本模型中共存在V×V=32×32=1 024种不同的有序词汇组合,因此,在实验中,使用大小为V×V=1 024维的词向量E描述表达式的特征,即
| $ {\mathit{\boldsymbol{e}}_i} = {\mathit{\boldsymbol{\theta }}_a} \times \mathit{\boldsymbol{\theta }}_b^{\rm{T}} $ | (6) |
其中a和b分别表示表达式中的2个流线分段. θa与θb分别为表达式中2个流线分段对应的独热向量.各个不同的词汇组合与ei中的不同元素一一对应.
依据各对流线分段的空间距离为各表达式的特征词向量赋权.将流线中各分段上沿流线长度的中点定义为各分段的中点,考虑到分段中点距离较远的表达式对流线的特征具有更大的影响,为分段中点距离较远的表达式赋予更大的权重,将各分段的中点距其所属流线起始端点的距离称为分段的位置di,将各表达式的权重定义为
| $ {w_i} = \frac{{\left| {{d_a} - {d_b}} \right|}}{l} $ | (7) |
其中:l为流线的长度,da和db分别为该表达式对应分段的位置.
将各表达式的特征词向量加权后按位相加,以计算流线X的特征词向量,即
| $ \mathit{\boldsymbol{B}} = \sum\limits_{a \in X} {\sum\limits_{b \in Z} {{w_i}} } {\mathit{\boldsymbol{e}}_i} $ | (8) |
传统流线查询方法依赖传统的流线相似度算法,考虑流线间的空间位置关系,如最近距离、各点平均距离等,只能用于查询目标流线附近的流线,而不能查找距离目标流线较远,但形状与目标流线类似的流线,故可基于流线特征化方法的流线查询算法.
以TF-IDF (term frequency-inverse document frequency)模型为各表达式赋权.采用空间敏感的词袋模型,着重考虑表达式出现与否,并为其每次出现赋权,而非直接计算句子中表达式出现的数量.因此,简化TF-IDF模型,以含有各词汇的流线占流线总数的比例作为各词汇的频率fi.在本模型中,以频率对数的绝对值做为各个表达式的权重,即
| $ {W_i} = \log \frac{1}{{{f_i}}} $ | (9) |
结合表达式的权重比较流线对的相似度.与上述流线的特征词向量一致,将各表达式的权重以相同的方式排列成长度为V×V=1 014维的词向量W,则流线对X、Y的不相似度词向量为
| $ \mathit{\boldsymbol{D}}(X, Y) = \mathit{\boldsymbol{W}}|\mathit{\boldsymbol{B}}(X) - \mathit{\boldsymbol{B}}(Y)| $ | (10) |
该不相似度词向量上各元素的绝对值即为该流线对上各表达式对的不相似度,差异越大,其特征词向量之差的绝对值越大.考虑到不相似度词向量的对称性,将流线对的不相似度标量定义为
| $ d(X, Y) = \sum\limits_i^{\frac{{V(V + 1)}}{2}} {{W_i}} |\mathit{\boldsymbol{B}}{(X)_i} - \mathit{\boldsymbol{B}}{(Y)_i} $ | (11) |
移除流场中的部分流线,不会显著影响流场的特征,而移除其他流线则会影响流场的特征.反之,加入特定的流线可显著增加与原始流场的相似度.反复加入流线即可得与原始流场相似度依次递增的流场,此即一组压缩流场.
引入贪心算法,向空流场加入最能提高压缩流线集内各流线间不相似度的流线.将压缩流场每对流线的相似度的和称为压缩流线集的相似度,将目标压缩流场的流线条数称为目标流场大小,将不在压缩流线集中而在流场中的流线称为外部流线.
算法 2 压缩流线集合
S:=Ø//初始化压缩流线集合为空集
MaxDissim := 0 //初始化最大不相似度为0
For streamline x in dataset:
For streamline y in S:
If Dissim(x, y) > MaxSim:
MaxSim := Dissim(x, y)
S={x, y} //将压缩流线集视为{x, y}
While card(S) < N:
TmpLine:=None //初始化当前最不相似流线
MaxDissim :=0 //初始化最大不相似度为0
For streamline x in dataset:
TmpDissim:=0 //初始化不相似度为0
For streamline y in S:
TmpDissim:=TmpDissim + Dissim(x, y)
If TmpDisism > MaxDissim:
TmpLine:=x
S:=S∪{x} //将x加入S
3 实验 3.1 数据集预处理采用SLVG数据集、IEEE Visualization 2004 Contest数据集、carotid数据集和velocityMag数据集,以检验不同场景下的性能.
3.1.1 SLVG数据集SLVG数据集由2个的随机生成的流场组成,即108CP流场和5CP流场,其分别包含108个临界点和5个临界点.各采样点组成立方体,其每条边均由51个采样点组成,即51×51×51个采样点.
3.1.2 IEEE Visualization 2004 Contest数据集IEEE Visualization 2004 Contest数据集为计算机模拟的龙卷风,包含40个时间片、500×500×100个采样点,覆盖2 139×2 004×19.8 km3的空间.
3.1.3 carotid数据集carotid数据集的采样点分布在76×49×45的空间中,共包含174 195个采样点.本数据集富含漩涡,其流线的曲率大,流场十分复杂.
3.1.4 velocityMag数据集velocityMag数据集的采样点分布在57×33×25的空间中,共47 025个采样点.其流线分布在一个不规则三维空间内,流线弯曲而可见明显的临界点.
3.2 实验结果及分析在各个测试数据集上执行所述算法,观察经管道化后的流线特征.
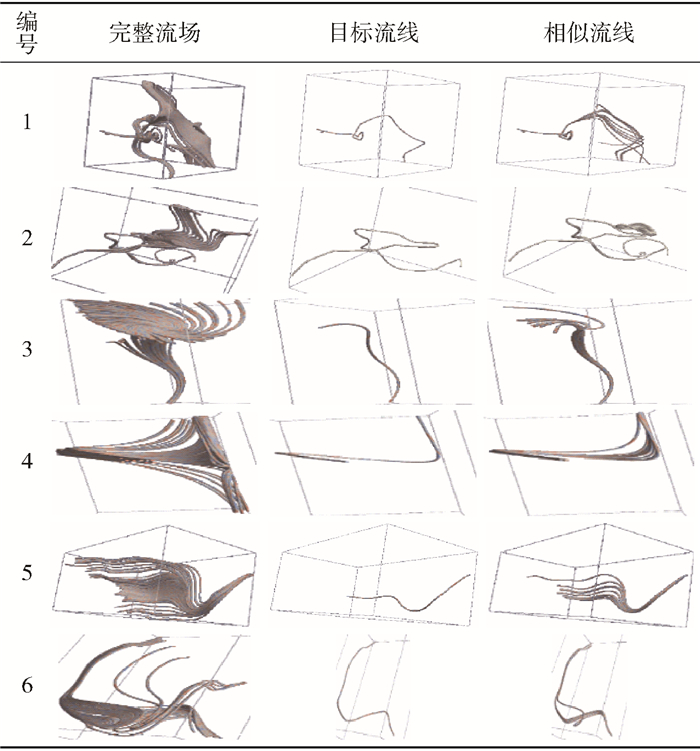
3.2.1 流线查询选定一条流线作为目标流线,在流场中查找与其最相似的若干条流线.在本实验中,查找最相似的10条流线,实验结果如表 1所示.第1组样例取自carotid数据集,算法准确地查询到了图形中部环绕关键点的10条相似流线;第2组样例取自carotid数据集,算法查询到了以形状相似的路径环绕各个关键点的10条流线;第3组样例取自SLVG数据集,考虑到流线中下部存在数个弯曲部分,故流线上部的不同的弯曲方向将对应不用的流线特征,依据选取的流线,算法成功查询到了10条弯曲方向类似的流线;第4组样例取自SLVG数据集,与第3组样例类似,算法查询到的10条流线不仅仅是弯曲方向类似的流线,还是弯曲程度最接近目标流线的流线;第5组样例取自velocityMag数据集,算法查询到了依次呈现相似的弯折段的10条流线;第6组样例取自velocityMag数据集,与第5组类似,算法查询到了与目标流线形状类似的10条流线.
|
|
表 1 流线查询的实验结果 |
使用上述流场压缩算法,依次构建大小为64、32、16、8线的压缩流线集.流场压缩的实验结果如表 2所示.第1组样例取自SLVG数据集,算法组合了流经不同路径的流线,在尽可能保留环等流场特征的情况下完成了流场压缩的任务;第2组样例取自SLVG数据集,算法组合了不同位置成环的流线,准确完成了流线压缩任务;第3组样例取自SLVG数据集,算法区分了走向不同方向的流线,在压缩流场的同时保持了流线上下分布的特征;第4组样取自SLVG数据集,算法保留了顶部漩涡状的结构;第5组样例取自SLVG数据集,算法分别保留了顶部的弯折结构、中部的流面和底部的流管特征;第6组样例取自IEEE Visualization 2004 Contest数据集,算法保留了弯曲程度不同的流线,保持了龙卷风的特征.
|
|
表 2 流场压缩的实验结果 |
所述算法采用数据驱动的策略,使用在三维流场中广泛撒点获取的流线集合,基于几何特征和空间特征将所得流线特征化后,通过加权后的流线特征计算流线间的相似度,继而准确完成了流线查询和流场压缩的任务.
| [1] |
McLoughlin T, Laramee R S, Peikert R, et al. Over two decades of integration-based, geometric flow visualization[J]. Computer Graphics Forum, 2010, 29(6): 1807-1829. DOI:10.1111/j.1467-8659.2010.01650.x |
| [2] |
Ye Xiangong, Kao David, Pang Alex. Strategy for seeding 3D streamlines[C]//IEEE Visualization. Minneapolis: [s.n.], 2005: 471-478.
|
| [3] |
Edmunds M, Laramee R S, Malki R, et al. Automatic stream surface seeding:a feature centered approach[J]. Computer Graphics Forum, 2012, 31(3pt2): 1095-1104. DOI:10.1111/j.1467-8659.2012.03102.x |
| [4] |
郭雨蒙, 王文珂, 李思昆. 基于相似度引导的流线种子点并行分布方法[J]. 系统仿真学报, 2014, 26(9): 2155-2159. Guo Yumeng, Wang Wenke, Li Sikun. Parallel strategy of streamline seeding with similarity-guiding[J]. Journal of System Simulation, 2014, 26(9): 2155-2159. |
| [5] |
Marchesin S, Chen C K, Ho C, et al. View-dependent streamlines for 3D vector fields[J]. IEEE Transactions on Visualization and Computer Graphics, 2010, 16(6): 1578-1586. DOI:10.1109/TVCG.2010.212 |
| [6] |
李春鑫, 彭认灿, 高占胜, 等. 一种改进的三维流场数据可视化方法[J]. 武汉大学学报(信息科学版), 2017, 42(6): 744-748. Li Chunxin, Peng Rencan, Gao Zhansheng, et al. An improved legible method for visualizing 3D flow field[J]. Geomatics and Information Science of Wuhan University, 2017, 42(6): 744-748. |
| [7] |
Li Yifei, Wang Chaoli, Shene C K. Extracting flow features via supervised streamline segmentation[J]. Computers & Graphics, 2015(52): 79-92. |
| [8] |
Yu H, Wang C, Shene C K, et al. Hierarchical streamline bundles for visualizing 2D flow fields[C]//IEEE VisWeek 2010 Posters. Salt Lake City: [s.n.], 2010.
|
| [9] |
Rossl C, Theisel H. Streamline embedding for 3D vector field exploration[J]. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(3): 407-420. DOI:10.1109/TVCG.2011.78 |
| [10] |
Liu Shiguang, Song Hange. Streamline querying based on finite substructures[J]. Journal of Visualization, 2019, 22(3): 571-585. DOI:10.1007/s12650-019-00552-x |
| [11] |
Li Yifei. Extracting flow features using bag-of-features and supervised learning techniques[D]. Michigan: Open Access Dissertation, Michigan Technological University, 2015.
|
| [12] |
Han Jun, Tao Jun, Zheng Hao, et al. Flow field reduction via reconstructing vector data from 3D streamlines using deep learning[J]. IEEE Computer Graphics and Applications, 2019, 39(4): 54-67. DOI:10.1109/MCG.2018.2881523 |
| [13] |
Wang Zhongjie, Martinez Esturo J, Seidel H P, et al. Pattern search in flows based on similarity of stream line segments[C]//Proc Vision, Modeling and Visualization. Darmstadt, Germany: [s.n.], 2014: 23-30.
|
| [14] |
Li Yifei, Wang Chaoli, Shene C K. Streamline similarity analysis using bag-of-features[C]//Proc SPIE 9017, Visualization and Data Analysis 2014. San Francisco, California: [s.n.], 2014: 90170N.
|
| [15] |
Tang Bin. Parallel visualization of flow field based on streamline similarity[J]. International Journal of Performability Engineering, 2018, 14(4): 717-728. |
| [16] |
Han Jun, Tao Jun, Zheng Hao, et al. Flow field reduction via reconstructing vector data from 3D streamlines using deep learning[J]. IEEE Computer Graphics and Applications, 2019, 39(4): 54-67. DOI:10.1109/MCG.2018.2881523 |
| [17] |
Han Jun, Tao Jun, Wang Chaoli. FlowNet: a deep learning framework for clustering and selection of streamlines and stream surfaces[EB/OL]. 2018(2018-11-12)[2019-05-23]. https://doi.org/10.1109/TVCG.2018.2880207.
|