锚节点的布设方案决定了无线传感器网络的定位极限.针对现有布设算法存在计算开销大和优化策略具有局限性等问题,提出了基于天牛须搜索的锚节点布设优化算法.采用向量化的克拉美罗下界作为布设优化策略,通过功效系数法优化布设策略,并采用天牛须搜索算法实现布设的快速、精确收敛.仿真结果表明:与传统区域定位误差均界评价指标相比,所提算法使得99.74%的区域内定位性能极限提升了约38.79%;在25锚节点布设场景下,与遗传算法相比,布设后区域内定位性能极限大致相同,但搜索时间降低了约64.2%.
The anchor node layout scheme determines the performance of localization in the wireless sensor network. In order to solve the problems of high computational cost and limited optimization strategy of existing layout algorithms, an anchor node layout optimization algorithm based on the beetle antennae search was proposed. The algorithm adopts Cramér-Rao lower bound vector as the optimization strategy, and the efficiency coefficient method to optimize the layout strategy and then the algorithm uses beetle antennae search algorithm to achieve rapid deployment of anchor node. The simulations show that the proposed algorithm reduces the low bound of localization performance by 38.79% in 99.74% of the regions, and in the 25-anchor node layout scenario, compared with the genetic algorithm, the low bound of localization performance is almost same, but the search time is reduced by about 64.2%.
随着大数据时代的到来,无线传感器网络作为主要的数据来源之一,其采集数据的有效性、可靠性对大数据时代发展具有重要意义,对于大多数应用,如环境、工业监测、交通控制、病人健康监测等来说,没有位置信息的数据是没有意义的[1].对于无线传感器网络本身而言,节点的位置信息可以提升自组网络的路由效率[2].
基于无线测距的传感器网络定位系统大多使用固定或移动位置的锚节点通过三角、双曲线或球形三边测量原理来实现区域内未知节点的定位[3].目前,实现锚节点最优布设的研究工作主要集中在布局优化策略、优化的目标、候选锚节点空间以及单个目标位置和整个待定位区域等方面[4].
Lasla等[5]提出了基于残余区域的锚节点布设方法,利用最小化残余区域作为布设优化指标,但是需要较高的锚节点覆盖密度. Liu等[6]提出了一种均方误差下限作为锚节点布设评价指标,并基于松弛法实现节点快速布设,但缺少对布设后整个区域性能分析. Miao等[7]从理论和仿真模拟研究了锚节点在圆形区域均匀分布且各个锚节点距离有关的测距噪声条件下的锚节点最优分布问题,证明了在有限的锚节点布设场景下,与距离无关的测距噪声下最佳锚节点分布并不满足在覆盖区域等间距布设,并提出了基于费雪信息矩阵的评价标准.汪晗等[8]提出了区域定位误差均界指标作为优化目标,并分析了布设质心、几何形状、几何面积对区域定位精度影响,仍然限定了锚节点位置,同时缺少锚节点候选空间网格大小对最终区域定位性能影响分析.
针对现有锚节点布设优化在优化目标单一和锚节点候选空间限定问题,结合机器学习中多目标优化算法思想和启发式算法可在短时间内求解最优解的优点,笔者提出了一种基于天牛须搜索的锚节点布设优化算法,通过网格稀疏化和定位误差的克拉美罗下界(CRLB,Cramér Rao lower bound)构建区域定位评价向量,利用功效系数法优化目标函数,通过天牛须搜索算法实现锚节点的最优布设搜索.
1 锚节点定位误差界CRLB是衡量参数无偏估计量的方差的下限,通常用于衡量定位系统的定位性能上限[9].基于测距的定位方式推导了无线传感器网络中单目标的定位误差界.
考虑基于测距的二维平面无线传感器网络中单目标节点的定位问题.网络中包含n个锚节点,所有锚节点组成的集合用A表示;锚节点i的位置向量表示为θi=(xi, yi),所有锚节点位置向量组成的集合表示为θ={θi|i∈A};目标节点o与第i个锚节点之间的距离测量值zi表示为
| $ \begin{array}{*{20}{c}} {{z_i} = {{\left\| {{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_i}} \right\|}_2} + {e_i} = }\\ {\sqrt {{{\left( {{x_o} - {x_i}} \right)}^2} + {{\left( {{y_o} - {y_i}} \right)}^2}} + {e_i},i \in A} \end{array} $ | (1) |
其中:‖·‖2为L2范数,ei为测距误差.考虑在视距环境下,测距误差ei服从零均值和σi2方差的高斯分布[10].定义Z={zi|i∈A}表示目标节点与所有相邻锚节点i测距集合,则所有测量值的联合概率密度函数可表示为
| $ p\left( {Z;\theta } \right) = \prod\limits_{i \in \mathit{\boldsymbol{A}}} {p\left( {{z_i};{\mathit{\boldsymbol{\theta }}_i},{\mathit{\boldsymbol{\theta }}_o}} \right)} $ | (2) |
其中
| $ \begin{array}{*{20}{c}} {p\left( {{z_i};{\mathit{\boldsymbol{\theta }}_i},{\mathit{\boldsymbol{\theta }}_o}} \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}\sigma _i^2} }} \times }\\ {\exp \left\{ { - \frac{{{{\left( {{z_i} - {{\left\| {{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_i}} \right\|}_2}} \right)}^2}}}{{2\sigma _i^2}}} \right\}} \end{array} $ | (3) |
则待估计参数θo对应的费雪信息H表示为[11]
| $ \mathit{\boldsymbol{H}} = - E\left\{ {{\nabla _{{\mathit{\boldsymbol{\theta }}_o}}}{{\left[ {{\nabla _{{\mathit{\boldsymbol{\theta }}_o}}}p\left( {Z;\theta } \right)} \right]}^{\rm{T}}}} \right\} $ | (4) |
其中
根据CRLB的定义及式(2)~式(4),推导可得单目标节点的位置估计误差的方差CRLB为
| $ R\left( {\theta ,{\mathit{\boldsymbol{\theta }}_o}} \right) = \text{tr}\left( {{\mathit{\boldsymbol{H}}^{ - 1}}} \right) = \text{tr}\left( {{{\left( {\mathit{\boldsymbol{GC}}{\mathit{\boldsymbol{G}}^{\rm{T}}}} \right)}^{ - 1}}} \right) $ | (5) |
其中
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {1/\sigma _1^2}&0&0&0\\ 0&{1/\sigma _2^2}&0&0\\ 0&0& \ddots &0\\ 0&0&0&{1/\sigma _n^2} \end{array}} \right] $ | (6) |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_1}}}{{{{\left\| {{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_1}} \right\|}_2}}}}&{\frac{{{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_2}}}{{{{\left\| {{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_2}} \right\|}_2}}}}& \ldots &{\frac{{{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_n}}}{{{{\left\| {{\mathit{\boldsymbol{\theta }}_o} - {\mathit{\boldsymbol{\theta }}_n}} \right\|}_2}}}} \end{array}} \right] $ | (7) |
当各个测距误差ei服从零均值和σm2方差的高斯分布时,式(6)可以简化为
| $ \mathit{\boldsymbol{C}} = \frac{1}{{\sigma _m^2}}{\mathit{\boldsymbol{I}}_{n \times n}} $ | (8) |
其中In×n为n阶单位矩阵.则有
| $ R\left( {\theta ,{\mathit{\boldsymbol{\theta }}_o}} \right) = \text{tr}\left( {{{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{G}}^{\rm{T}}}} \right)}^{ - 1}}} \right)\sigma _m^2 $ | (9) |
式(9)表明了测距误差的方差σm2被权系数tr((GGT)-1)放大后转变成定位误差的方差,即基于测距的无线传感器网络定位精度与测距误差方差σm2和矩阵G有关.因此,锚节点的布设优化依据需要从测距误差方差和矩阵G角度综合考虑.
2 天牛须寻优搜索算法 2.1 问题描述无线传感器网络的锚节点最优布设主要存在区域定位精度表征和节点布设优化2个挑战.具体原因如下.
1) 在无线传感器网络大多数应用场景中,包含了大量的固定或移动节点,因此锚节点布设中需要考虑区域定位精度问题,即多个待定位节点在区域B内随机分布时,锚节点布设对多个待定位节点的定位精度影响.在上述第1节中,分析了单个待定位节点的误差下界,考虑各个待定位节点之间位置独立,则只需分析区域范围内每个点处的定位误差下界CRLB即可.
2) 当锚节点布设位置改变时,对于特定位置处的待定位节点的CRLB也随之发生变化,同时在锚节点布设确定时,不同位置处的CRLB也不同,最终导致了锚节点布设所需搜索空间庞大,有限时间内难以实现最优布设.同时传统的标量指标也难以全面精确地表征传感器网络区域内定位精度.
针对上述2个问题,基于网格稀疏化和多目标优化的解决思路,将区域B离散化,并用网格中心点处的位置估计误差方差CRLB向量的Ra(θ, X)=[R(θ, X1) R(θ, X2) … R(θ, XK)]来表征区域定位精度,并将锚节点布设优化转化为多目标优化问题,即
| $ \begin{array}{*{20}{c}} {\min {R_a}\left( {\theta ,X} \right)}\\ {{\rm{Subject}}\;{\rm{to}}:\theta \subset B} \end{array} $ | (10) |
其中Xi(i=1, 2, …, K)表示为K个网格中心点的位置坐标.为优化式(10)中的目标函数,将有约束最优化转化为无约束优化问题,采用惩罚函数法,增加惩罚因子α,将上述优化问题转化为
| $ \begin{array}{*{20}{c}} {\min F\left( {\theta ,X} \right) = }\\ {\left[ {\begin{array}{*{20}{c}} {{F_1}\left( {\theta ,{\mathit{\boldsymbol{X}}_1}} \right)}&{{F_2}\left( {\theta ,{\mathit{\boldsymbol{X}}_2}} \right)}& \cdots &{{F_K}\left( {\theta ,{\mathit{\boldsymbol{X}}_K}} \right)} \end{array}} \right] = }\\ {{R_a}\left( {\theta ,X} \right) + \alpha \mathit{\Phi }\left( \theta \right)} \end{array} $ | (11) |
其中:Φ(θ)=[φ(θ1) φ(θ2) … φ(θK)],φ(θi)(i=1, 2, …, K)为外部罚函数,定义如下:
| $ \varphi \left( {{\mathit{\boldsymbol{\theta }}_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{{\mathit{\boldsymbol{\theta }}_i} \in B}\\ {1,}&{{\mathit{\boldsymbol{\theta }}_i} \notin B} \end{array}} \right. $ | (12) |
当传感器网络不满足定位所需要的多重覆盖区域,CRLB趋近于无穷大,即上述目标函数同时对定位所需多重覆盖和区域内定位性能进行了约束.
由于多目标优化是针对向量函数的优化,优化过程中需要从向量的角度比较2个解之间优劣,一般情况下难以比较[12].通常采用方法是将求解问题进行适当转化处理,为此引入一种功效系数法,将向量函数F(θ, X)中各个子项转化到一个统一目标函数,并将该目标函数f(θ, X)作为多目标优化问题的评价函数.该方法将向量函数F(θ, X)中每个子项Fi(θ, Xi)(i=1, 2, …, K)都通过功效系数ηi(0≤ηi≤1)来表示该子项的优劣程度.当ηi=0时,表示子项Fi(θ, X)达到最优,反之当ηi=1时,Fi(θ, X)达到最劣,总功效系数定义为所有子项功效系数的几何平均值[13],则最终多目标最优化问题转化为
| $ \begin{array}{*{20}{c}} {\max f\left( {\theta ,X} \right) = \sqrt[K]{{{\eta _1}{\eta _2} \cdots {\eta _K}}}}\\ {{\eta _i} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{F_i}\left( {\theta ,{\mathit{\boldsymbol{X}}_i}} \right)}}{M},}&{{F_i}\left( {\theta ,{\mathit{\boldsymbol{X}}_i}} \right) < M}\\ {1,}&{{F_i}\left( {\theta ,{\mathit{\boldsymbol{X}}_i}} \right) \ge M} \end{array},i = 1,2, \cdots ,K} \right.} \end{array} $ | (13) |
最后通过天牛须搜索算法求解式(13)最优化问题.
2.2 算法流程基于梯度的优化算法尽管具备更加高效的计算效率,但是需要梯度信息,而由于区域内每个点的CRLB的梯度与解相关,且形式与该点处的信号覆盖有关,也即梯度函数不具备确定形式,因此在实际优化中不具备可操作性.
天牛须搜索是Jiang等[14-15]受到天牛觅食行为提出的一种智能优化算法,相对于传统梯度下降、牛顿法等基于梯度的优化算法,不需要经过复杂的梯度计算就能高效实现全局寻优;相对于模拟退火、遗传算法等启发式算法,只需要一个天牛个体,大大降低了优化的计算复杂度,为无线传感器定位网络的快速、高精度和高效部署提供可行性.
基于天牛须搜索的锚节点布设优化算法分为搜索和检测2个阶段.其中,搜索阶段是通过式(14)定义的左侧和右侧的搜索行为来模拟天牛觅食中的寻找食物气味方向:
| $ \left. {\begin{array}{*{20}{l}} {{\theta ^{\rm{r}}} = {\theta ^t} + {d^t}b}\\ {{\theta _1} = {\theta ^t} - {d^t}b} \end{array}} \right\} $ | (14) |
其中:θl和θr分别表示天牛的左须和右须坐标;d为天牛2个触角之间的距离,即感知距离,与算法的搜索性能有关,d越大对应的搜索区域也越大,但是对应搜索精度也越差,因此需要随着算法搜索次数逐步调低距离d,以提高初始搜索区域大小和全局解精度;b为单位化的随机向量集合,其增强该算法的搜索能力,随机向量bi可表示为
| $ {\mathit{\boldsymbol{b}}_i} = \frac{{\text{rnd}\left( 2 \right)}}{{{{\left\| {\text{rnd}\left( 2 \right)} \right\|}_2}}},i = 1,2, \cdots ,n $ | (15) |
其中:rnd(·)表示随机数生成函数,n为区域B内待布设的锚节点数量.
检测阶段用来判断天牛个体的运动方向和运动距离,其迭代模型表示为
| $ {\theta ^t} = {\theta ^{t - 1}} + {\delta ^t}b \text{sign}\left( {F\left( {{\theta ^{\rm{r}}},X} \right) - F\left( {{\theta ^1},X} \right)} \right) $ | (16) |
其中:δ为搜索步进,与算法的收敛速度和搜索精度有关,为保证收敛速度和精度需要随着迭代次数t递减;sign(·)表示符号函数.
由以上算法流程可知,搜索步进δ和感知距离d对算法搜索性能至关重要,并且固定大小的δ和d无法同时满足算法的快速收敛和精确全局解.在机器学习领域中常采用一个根据迭代次数衰减的学习率,来兼顾收敛速度和全局解精度[16],为此,引入指数衰减模型来不断更新δ和d值,衰减模型为
| $ \left. {\begin{array}{*{20}{l}} {{d^t} = {d^0}a_{{d^d}}^{\frac{t}{T}}}\\ {{\delta ^t} = {\delta ^0}a_{{\delta ^\delta }}^{\frac{t}{T}}} \end{array}} \right\} $ | (17) |
其中:d0和δ0分别为感知距离和搜索步进的初始值,ad和aδ为衰减系数,Td和Tδ为指数衰减时间常数,t为搜索迭代次数.
基于天牛须搜索的锚节点布设优化算法流程具体如下:
算法1 基于天牛须搜索的锚节点布设优化算法
输入:损失函数F(θ, X);初始参数值:θ0,d0,δ0,M
输出:θbest
While t < Tmax or停止条件do
根据式(15)更新方向单位向量集合b;
根据式(14)用两侧触角在变量空间中搜索;
根据式(16)更新当前搜索状态θt;
if f(θt, X) < fbest then
θbest=θt;
根据式(17)更新感知距离dt和步进δt return θbest
3 仿真分析 3.1 仿真环境首先在10 m×11 m大小的矩形区域内进行6个锚节点的布设实验,分析网格大小、区域定位精度评价指标2种因素对天牛须的无线传感器网络布设优化算法的性能影响程度;然后在21 m×21 m大小的区域内进行6、8、10、15、25个锚节点布设下算法复杂度和基于天牛须的搜索性能对比.仿真假设单个节点的覆盖半径为20 m,无线信号测距误差独立同分布,测距误差1 m(1σ).
3.2 网格大小因素为分析表征区域定位精度指标中网格大小对本文算法的影响程度,以0.1 m为步进,借助箱线图,通过仿真分析0.1~2.5 m范围内的网格布局优化后区域内CRLB统计分布,如图 1所示.
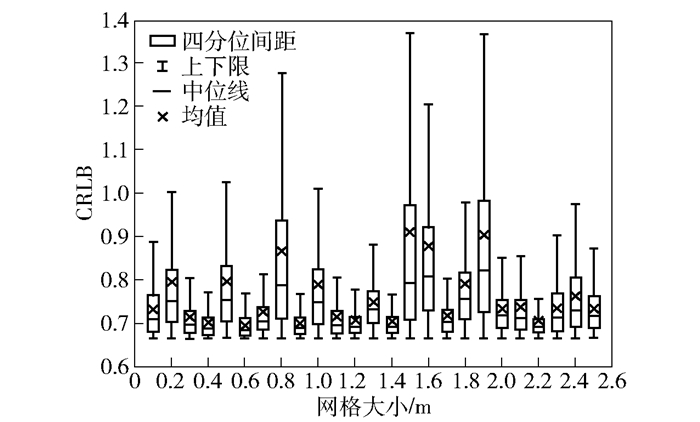
|
图 1 网格大小对布局优化性能影响仿真结果 |
由图 1可以看出,不同网格大小的区域内CRLB大致整体分布在0.66~1.35之间,网格大小对区域内CRLB分布影响较大,同时随着网格的增大,区域内CRLB分布变化更加随机,CRLB统计分布也越差,但是都能将CRLB分布控制在一定范围内.
3.3 区域定位精度评价指标因素为分析所提出的区域定位精度评价指标的有效性,在0.4 m网格大小和相同初始分布条件下,对比了区域误差均界和所提出的向量化区域指标的布设结果与性能,仿真结果如图 2~图 4所示.

|
图 2 误差均界和向量化区域指标布设结果 |
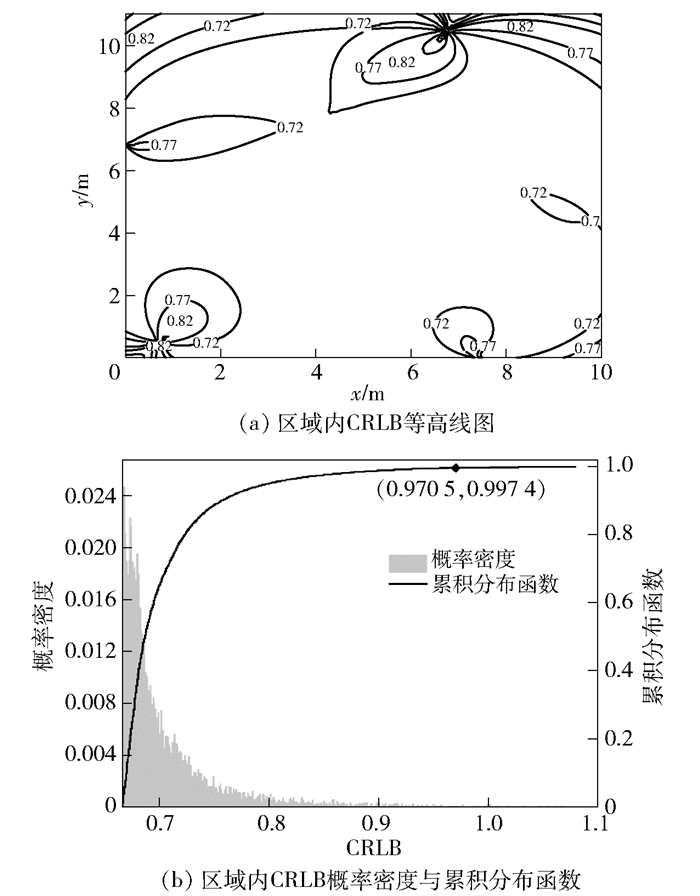
|
图 3 向量化区域指标的布设结果与性能 |

|
图 4 误差均界指标的布设结果与性能 |
从图 3(a)、图 4(a)中可以看出,相对区域定位误差均界,所提出的向量化CRLB评价指标在定位区域中心更加平缓,较大定位误差的区域面积更小.通过对比图 3(b)和图 4(b)的结果可以得出,相对于区域定位误差均界,笔者提出的向量化CRLB评价指标可以将99.74%定位区域范围内的CRLB降低约38.79%.
3.4 搜索算法性能为分析算法搜索性能,在21 m×21 m大小区域内6、8、10、15、25个锚节点布设情况下,对不同算法的搜索能力及布设性能进行分析,仿真结果如图 5和图 6所示.可以看出,在搜索时间方面,随着锚节点数量的增多,基于遗传算法的锚节点布设算法搜索时间呈线性增长,模拟退火算法搜索时间略微增加,而本文算法基本平稳不变,在25个锚点布设情况下,本文算法搜索时间相较遗传算法,降低约64.2%.从区域内布设定位性能来看,随着锚节点数量增加,本文算法相对于模拟退火算法和遗传算法,布设后区域内定位误差从小到大的顺序大致为本文算法≈遗传算法>模拟退火算法.综上,在算法复杂度和布设性能方面,本文算法在锚节点数量较多时具有更大优势.
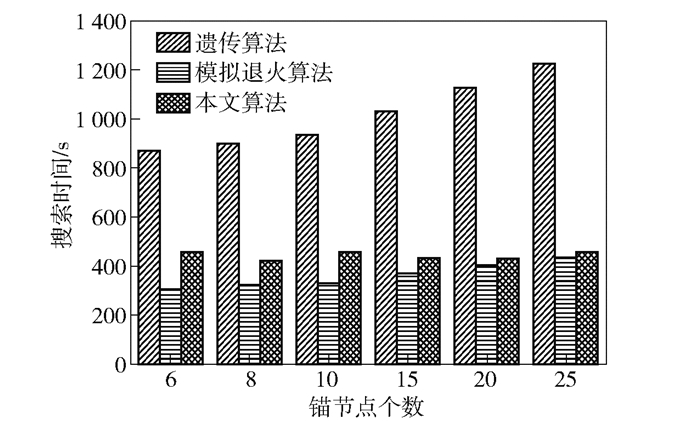
|
图 5 不同算法的搜索时间结果 |

|
图 6 不同算法时98%区域的定位误差(1σ) |
分析了单点目标定位误差,并以此为基础,提出了向量化区域误差指标,将锚节点布设优化问题转化为多目标优化问题,建立了锚节点布设优化目标函数,为满足天牛须搜索算法的基本要求,通过功效系数法对目标函数进行了优化处理,最终实现锚节点布设优化.从网格大小选取、指标选取和搜索算法方面分析了基于天牛须搜索的锚节点优化性能.仿真结果表明,本文算法与经典遗传算法相比布设区域内节点定位性能几乎相同,但计算开销明显减少.
尽管提出的向量化区域评价指标和布设优化算法在算法复杂度、区域定位性能提升方面都具有很大的优势,但是需要考虑实际场景下多径对测距的影响,对于测距误差在实际情况下很难满足独立高斯分布,同时由于墙面等反射造成的多径会导致测距误差分布与待定位点位置有关,而笔者为便于讨论布设优化算法,考虑了理想情况下的测距误差.在后续研究中,拟研究室内多径建模方法与测距误差模型,在此基础之上,完成对目标函数的修正与完善.
| [1] |
Han Guangjie, Xu Huihui, Duong T Q, et al. Localization algorithms of wireless sensor networks:a survey[J]. Telecommunication Systems, 2013, 52(4): 2419-2436. DOI:10.1007/s11235-011-9564-7 |
| [2] |
Paul A K, Sato T. Effective data gathering and energy efficient communication protocol in wireless sensor network[C]//2011 The 14th International Symposium on Wireless Personal Multimedia Communications (WPMC). Istanbul: [s.n.], 2011: 1-5.
|
| [3] |
Liu Hui, Darabi H, Banerjee P, et al. Survey of wireless indoor positioning techniques and systems[J]. IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), 2007, 37(6): 1067-1080. DOI:10.1109/TSMCC.2007.905750 |
| [4] |
Wu Mou, Zhao Junzhe, Dai Wenhua, et al. A range-based adaptive target localization method in wireless sensor networks with mobile anchors[C]//2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC). Xi'an: [s.n.], 2018: 1205-1209.
|
| [5] |
Lasla N, Younis M, Ouadjaout A, et al. On optimal anchor placement for efficient area-based localization inwireless networks[C]//2015 IEEE International Conference on Communications (ICC). London: [s.n.], 2015: 3257-3262.
|
| [6] |
Liu Zhenyu, Dai Wenhan, Win M Z. Node placement for localization networks[C]//2017 IEEE International Conference on Communications (ICC). Paris: [s.n.], 2017: 1-6.
|
| [7] |
Miao Qing, Huang Baoqi. On the optimal anchor placement in single-hop sensor localization[J]. Wireless Networks, 2018, 24(5): 1609-1620. DOI:10.1007/s11276-016-1424-7 |
| [8] |
汪晗, 王坤, 路文进, 等. 无线传感器网络的锚节点优化布设算法[J]. 计算机工程, 2018, 44(8): 105-111. Wang Han, Wang Kun, Lu Wenjin, et al. Anchor node optimal deployment algorithm in wireless sensor network[J]. Computer Engineering, 2018, 44(8): 105-111. |
| [9] |
Chaffee J, Abel J. GDOP and the Cramer-Rao bound[C]//Proceedings of 1994 IEEE Position, Location and Navigation Symposium-PLANS'94. Las Vegas: [s.n.], 1994: 663-668.
|
| [10] |
Chepuri S P, Leus G. Sparsity-promoting sensor selection for non-linear measurement models[J]. IEEE Transactions on Signal Processing, 2015, 63(3): 684-698. DOI:10.1109/TSP.2014.2379662 |
| [11] |
Chan Y T, Ho K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915. DOI:10.1109/78.301830 |
| [12] |
Nyoman G, Ai Qingsong. A review of multi-objective optimization:methods and its applications[J]. Cogent Engineering, 2018, 5(1): 150-156. |
| [13] |
Tang Houxing, Fang Fang. A novel improvement on rank reversal in TOPSIS based on the efficacy coefficient method[J]. International Journal of Internet Manufacturing and Services, 2018, 5(1): 67. DOI:10.1504/IJIMS.2018.090591 |
| [14] |
Jiang Xiangyuan, Li Shuai. BAS: beetle antennae search algorithm for optimization problems[EB/OL]. 2017(2017-10-30)[2019-04-03]. https://arxiv.org/abs/1710.10724.
|
| [15] |
Jiang Xiangyuan, Li Shuai. Beetle antennae search without parameter tuning (BAS-WPT) for multi-objective optimization[EB/OL]. 2017(2017-11-07)[2019-04-03]. https://arxiv.org/abs/1711.02395.
|
| [16] |
Zeiler M D. ADADELTA: an adaptive learning rate method[EB/OL]. 2012(2012-12-22)[2019-05-01]. https://arxiv.org/abs/1212.5701.
|


