2. 中国金融认证中心, 北京 100054;
3. 机械工业仪器仪表综合技术经济研究所, 北京 100055
传统的流量工程策略的研究大多集中在构建和求解数学模型方面,其计算复杂度过高,为此,提出了一种经验驱动的基于多智能体强化学习的流量分配算法.该算法无需求解复杂数学模型即可在预计算的路径上进行有效的流量分配,从而高效且充分地利用网络资源.算法在软件定义网络控制器上进行集中训练,且在训练完成后再接入交换机或者路由器上分布式执行,同时也避免和控制器的频繁交互.实验结果表明,相对于最短路径和等价多路径算法,新算法有效减少了网络的端到端时延,并且增大了网络吞吐量.
2. China Financial Certification Authority, Beijing 100054, China;
3. Instrumentation Technology and Economy Institute, Beijing 100055, China
Most of the researches on traditional traffic engineering strategies focus on constructing and solving mathematical models. To reduce computational complexity, an experience-driven traffic allocation algorithm based on multi-agent reinforcement learning was proposed. It can effectively distribute traffic on pre-calculated paths without solving complex mathematical models and then fully utilize network resources. The algorithm performs centralized training on the software defined networking controller, and can be executed on the access switch or router in a distributed way after the training is completed. Frequent interactions with the controller are avoided at the same time. Experiments show that the algorithm is effective in reducing the end-to-end delay and increasing throughput of the network with respect to the shortest-path and the equal-cost multi-path.
软件定义网络(SDN,software defined network-ing)是近年来出现的一种新的网络体系架构,可将网元设备的控制平面和转发平面解耦,支持统一的接口对网络直接进行编程,可以灵活制定路由和转发策略.传统的基于SDN的流量工程主要是通过求解复杂的数学模型实现的[1],复杂度较高,求解时间过长,难以匹配流量的动态变化.随着机器学习在机器人控制、自动驾驶和Go[2]等方面取得的巨大成功,人们开始思考将网络控制和机器学习相结合. Mestres等[3]结合SDN、网络分析平台(NA,network analytics)、人工智能(AI,artificial intelligence)提出了一种新型的网络范式——知识定义网络(KDN,knowledge-defined networking). Chavula等[4]在SDN控制器中部署了基于Q-learning的流量工程策略,主要考虑了交换机之间逐跳的带宽和时延. Xu等[5]将深度强化学习算法应用到传统网络中,并以最大化系统的效用值函数为目标设计了奖励值.笔者提出了一种基于多智能体深度策略梯度(MADDPG, multi-agent deep deterministic policy gradient)算法的流量分配策略,该算法集中训练分布执行,其主要优势在于只需要局部状态信息就可以做出最优动作,节省了与控制器之间的交互时延,并且不需要知道环境的动力学模型.
1 强化学习基础强化学习[6]是机器学习的一种,通常由智能体和环境组成.智能体指的是学习者和动作执行者,在每个时刻t,智能体在它所处的环境观测到当前的状态st,做出动作at,从而使状态转移到st+1,伴随着状态转移智能体从环境中得到奖赏rt.强化学习的目标是找出一个策略π(st),以最大化累积折扣回报函数
深度强化学习(DRL,deep reinforcement learning)算法在近些年兴起,Mnih等[7]第1次将深度学习算法应用到强化学习上,提出了深度Q网络(DQN,deep Q network),对Q-learning进行了改进,使用函数逼近的方式对Q值函数进行表示,解决了Q-learning在状态空间很大的情况下Q表示过大的问题.但是DQN的缺点是只能解决动作空间有限的问题,实际中的控制问题往往是连续的,Lillicrap等[8]提出了一种基于Actor-Critic框架的深度确定性策略梯度(DDPG, deep deterministic policy gradient)算法,可用于解决连续动作空间上的问题. MADDPG[9]算法也是一种基于Actor-Critic的算法,具有3个特点:1)集中式训练,分散式执行,训练完成后使用时只需要知道局部信息就能给出动作;2)不需要知道环境的动力学模型;3)可以应用到合作或者竞争环境.
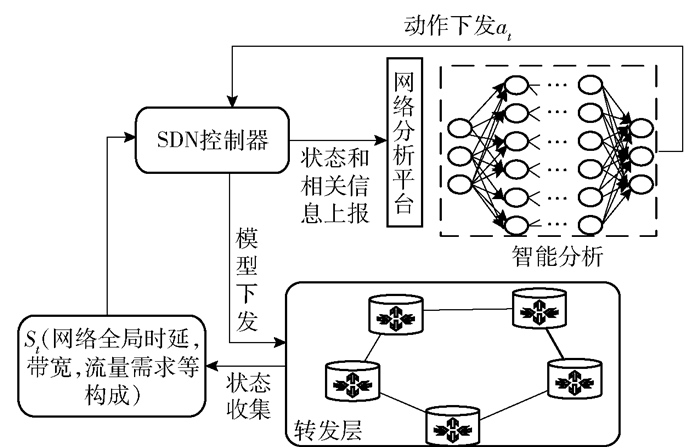
2 智能网络架构提出基于SDN的智能网络架构,如图 1所示,从下到上依次为转发层、控制层、智能决策层.转发层由支持软件编程的交换机组成,主要作用是转发处理数据包,通过南向接口和SDN控制器通信.控制平面主要连接底层硬件设备和智能决策层,同时获取全局的网络状态,例如网络拓扑、链路状况等.智能决策层主要用于产生流量工程(TE,traffic engineering)的控制策略,作为智能网络架构的核心,既可以在智能决策层上部署传统的TE算法,也可以部署人工智能算法.笔者主要讨论后者.网络分析平台负责收集网络的历史信息和即时信息,并且对这些信息进行加工处理,将其作为深度神经网络算法的输入.强化学习算法可以从这些大量的数据中学习到一个目标策略的模型.

|
图 1 基于SDN的智能网络架构系统框图 |
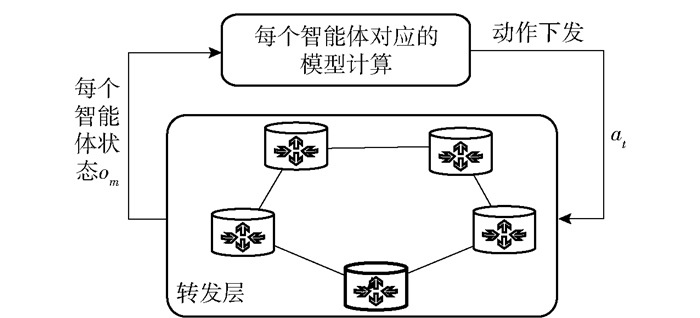
MADDPG算法特性很适合部署到智能网络架构中,智能决策平面通过控制平面收集到的网络信息完成集中训练.转发层中存在多个通信会话,每组通信会话的源端可以看成一个智能体.控制层收集所有会话的状态信息(系统全局的时延,吞吐量,流量需求等)上报给智能决策层训练,训练完成后决策层会将训练好的模型部署到网络的边缘交换机(智能体)上,每个智能体只需要知道自己的局部观测信息(单个会话的时延,吞吐量,流量需求等),就可以做出最优的决策,训练和执行过程分别如图 2和图 3所示.下文将进一步讲述该算法的细节以及在智能架构中的使用.
|
图 2 集中式训练过程 |
|
图 3 分布式执行过程 |
考虑一个具有M个端到端的通信会话网络,网络用一个有向图G(V,E)表示,其中V代表顶点的集合,E是所有边的集合,有向图中每个顶点代表一个交换机或者路由器,顶点之间的边代表一条链路.每一个会话包含一组源节点sm和目的节点dm,源、目的节点和多条候选路径用集合Pm表示,在这些源-目的(SD,source-destination)对之间有一定大小的流量Dm需要在Pm中的每条路径进行分配,am, j代表第m个会话在第j条路径上的分流比,
| $ U = \sum\limits_{m = 1}^M {\left[ {\log {x_m} - \log {z_m}} \right]} $ | (1) |
其中xm、zm分别代表第m个会话之间的吞吐量和时延. Xu等[5]尝试使用强化学习的方法来解决效用函数最大化的问题,在SDN环境中,可以在控制器中执行其所提出的DDPG-TE算法,但是如果控制器在训练完成之后出现故障时,流量调度策略不能再起到作用.提出的MADDPG-TE算法可以很好地解决这个问题,因为MADDPG是集中式训练,分布式执行,当控制器出现故障,MADDPG算法可以在源端交换机或者路由器利用其计算能力去执行算法,这并不需要太多的计算资源,算法训练好之后,做出决策非常容易.
3.2 基于MADDPG的TE算法设计DDPG采用的是一种actor-critic的训练框架,DDPG分别为actor网络、critic网络各创建2个神经网络拷贝,一个叫做online,一个叫做target.
| $ \begin{array}{l} {\rm{actor}}\;网络\left\{ {\begin{array}{*{20}{l}} {{\rm{online}}:\mu \left( {s|{\theta ^\mu }} \right)}\\ {{\rm{target}}:\mu '\left( {s|{\theta ^\mu }} \right)} \end{array}} \right.\\ {\rm{critic}}\;网络\left\{ {\begin{array}{*{20}{l}} {{\rm{online}}:{Q^\mu }\left( {s,a} \right)}\\ {{\rm{target}}:{Q^{\mu '}}\left( {s,a} \right)} \end{array}} \right. \end{array} $ | (2) |
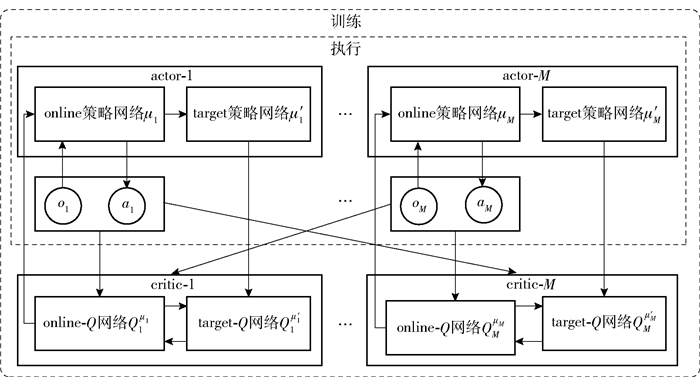
MADDPG采用了集中训练和分散执行的架构,从图 4中可以看出,其是一个由多个actor-critic组成的架构,在训练的时候,每个智能体的actor网络会获得局部的观测状态信息,而智能体的critic网络会获取本身的观测状态信息以及额外信息(一般是其他智能体的动作),进行集中式的全局训练.当模型训练完成后,只需要actor和环境进行交互,即可以获得最优的动作决策.
|
图 4 MADDPG算法框架 |
考虑一个有M个智能体的环境,π=(π1, π2,…,πM)代表M个智能体的策略,θ=(θ1, θ2,…,θM)表示M个智能体的策略参数,对于第m个智能体的累积,期望奖励可以写为
| $ J\left( {{\theta _m}} \right) = {E_{s \sim {\rho ^\pi },{a_m} \sim {\pi _m}}}\left[ {\sum\limits_{t = 0}^\infty {{r_{m,t}}} } \right] $ |
采用随机策略,则策略梯度可以写为
| $ \begin{array}{*{20}{c}} {{\nabla _{{\theta _m}}}J\left( {{\theta _m}} \right) = }\\ {{E_{s \sim {\rho ^\pi },{a_m} \sim {\pi _m}}}\left[ {{\nabla _{{\theta _m}}}\log {\pi _m}\left( {{a_i}|{o_i}} \right)Q_m^\pi \left( {s,{a_1}, \cdots ,{a_M}} \right)} \right]} \end{array} $ | (3) |
Qmπ(s, a1, …, aM)表示第m个智能体的状态-动作函数,不同智能体的Q是独立的,所以不同智能体可以设置不同结构的奖励值函数.
进一步地,根据文献[8],在确定性策略情况下,智能体在采用确定性策略μm的情况下,梯度公式使用链式法则拓展为
| $ \begin{array}{*{20}{c}} {{\nabla _{{\theta _m}}}J\left( {{\mu _m}} \right) = }\\ {{E_{\mathit{\boldsymbol{s}},a \sim B}}\left[ {{{\left. {{\nabla _{{\theta _m}}}{\mu _m}\left( {{a_m}|{o_m}} \right)Q_m^\mu \left( {s,{a_1}, \cdots ,{a_M}} \right)} \right|}_{{a_m} = {\mu _m}\left( {{o_m}} \right)}}} \right]} \end{array} $ | (4) |
上述梯度公式采用了Experience-Reply技术,其中B代表一个Buffer容器,其中包含了若干条信息,每一条信息用一个四元组(s, a, r, s′)表示.其中
| $ \begin{array}{*{20}{c}} {s = \left( {{o_1},{o_2}, \cdots ,{o_M}} \right),a = \left( {{a_1},{a_2}, \cdots ,{a_M}} \right),}\\ {r = \left( {{r_1},{r_2}, \cdots ,{r_M}} \right)} \end{array} $ |
om、am、rm分别代表第m个智能体的观测状态、行为和奖励值. actor网络采用上述的梯度使用梯度下降法进行更新. critic网络的更新方式可以由损失函数通过反向传播进行更新,其中损失函数为
| $ L\left( {{\theta _m}} \right) = {E_{s,a,r,s'}}\left[ {{{\left( {Q_m^\mu \left( {s,{a_1}, \cdots ,{a_M}} \right) - y} \right)}^2}} \right] $ | (5) |
其中:y=rm+Qmμ′(s′, a′1, …, a′M)|a′j=μ′j(oj),μ′={μ′1, μ′2, …, μ′M}是target策略的集合.
整个多智能体训练的过程跟单智能体训练过程相似.在训练完成后,actor可以通过自己的观测状态来采用相应的动作.将每个SD对的源端看成一个智能体,一共有M个智能体.下面介绍基于MADDPG的TE算法设计,首先设计了状态空间、动作空间和奖励值函数,随后基于智能网络架构设计了MADDPG-TE算法.
1) 状态空间:由每个智能体的观测信息组成s=(D1, D2, D3, …, DM),Dm代表第m个会话之间需要传送的流量需求.
2) 动作空间:每个智能体的分流比的集合.
| $ a = \left( {{a_{1,1}},{a_{1,2}}, \cdots ,{a_{m,j}}, \cdots ,{a_{M,\left| {{P_M}} \right|}}} \right) $ |
3) 奖励值函数:参考式(1),给每个智能体设置单独的奖励值,奖励值设置为rm=log xm-log zm,xm和zm分别是第m个会话的吞吐量和时延.
算法1 MADDPG-TE for M个智能体
1 初始化每一个智能体actor网络的online参数和critic网络的online参数,初始化状态s.
2 For t=1 to MAX-EPISODE do
对于每个agent,选择动作am=μm(om)+Nt, 其中om代表该智能体的观测状态,本文中即每个OD对的流量需求Dm,Nt代表探索所加的随机噪声.
3 每个智能体执行相应的流量分配动作am,得相应的奖励值r=(r1, r2, r3, r4, …,rM),进入下一个状态s′,s←s′.
4 存储(s, a, r, s′)到reply buffer B.其中a=(a1, a2, …, am)
For agent m=1 to M do
从B中进行mini-batch采样,采样大小为T,每个样本为(si, ai, ri, s′i)计算相应的yi=rmi+γQmμ′(s′i, a′1, …, a′M)
5 通过损失函数loss更新critic网络,其中Loss定义为
| $ \begin{array}{*{20}{c}} {L\left( {{\theta _i}} \right) = }\\ {{{\left. {\frac{1}{T}\sum {\left( {{y^i} - Q_i^\mu \left( {{s^i},a_1^i, \cdots ,a_M^i} \right)} \right)} } \right|}_{{a_m} = {\mu _m}\left( {o_m^i} \right)}}} \end{array} $ |
6 通过策略梯度公式更新actor网络.策略梯度的计算公式为
| $ \begin{array}{*{20}{c}} {{\nabla _{{\theta _i}}}J \approx }\\ {{{\left. {\frac{1}{T}\sum\limits_i {{\nabla _{{\theta _m}}}} {\mu _m}\left( {o_m^i} \right){\nabla _{{a_m}}}Q_m^\mu \left( {{s^i},a_1^i, \cdots ,a_M^i} \right)} \right|}_{{a_m} = {\mu _m}\left( {o_m^i} \right)}}} \end{array} $ |
End for
7 更新每个agent的target网络参数
| $ \theta _m^\prime \leftarrow \tau {\theta _m} + \left( {1 - \tau } \right)\theta _m^\prime $ |
End for
4 仿真和分析 4.1 仿真环境在仿真中,网络拓扑采用美国Abilene Network骨干网络,其含有11个网络节点和14条链路,实验中链路容量设置为固定大小的10 Mbit.使用python和Tensorflow去搭建深度学习网络以及进行模型的训练.通信会话的数量取M=5,候选路径集采用K-Shortest算法,其中K=3. OD对之间需要传输的流量连续不断地产生,服从均值为λ的泊松分布.
对端到端时延和吞吐量进行了建模估计.关于端到端时延模型,采用张峰等[11]提出的时延估算模型,主要考虑排队时延和发送时延,排队时延采用M/D/1排队模型,实验中节点发送数据包设置固定大小为8 kbit.发送时延为数据包第1个比特算起到最后一个比特发送完成的时间,发送时延大小为L/R,L为分组长度,R为链路容量,当分组长度L=8 kbit,链路容量R=10 Mbit,传输时延为0.78 ms.
当某条路径上的总流量超过链路容量,将丢弃大于链路容量的流量. L(e)为该链路的丢包率,则某条路径的丢包率为
| $ {x_m} = \sum\limits_j {{a_{m,j}}} {D_{\rm{m}}}{S_j} $ | (6) |
其中
从训练过程和不同算法性能的比较方面对实验结果进行分析.
1) 训练过程分析(Traffic为8 Mbit/s)
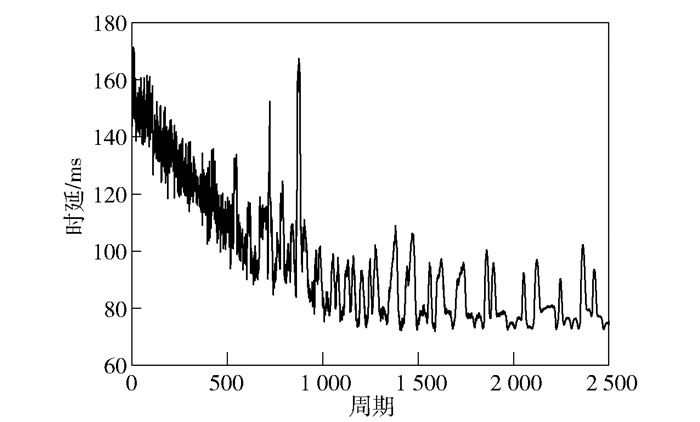
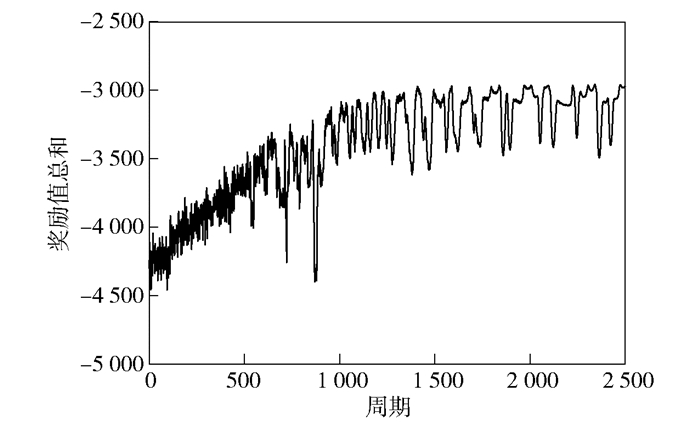
图 5所示为网络端到端时延随训练周期的变化.随着训练周期的增加,时延在减小,并趋于稳定. 图 6所示为每个智能体在训练过程中的奖励值随训练周期的变化,实验中一共存在5个智能体,奖励值分别记为r1~r5,单个智能体的奖励值在训练时候抖动性较大,但是奖励值的总和在2 000个周期之后相对稳定,基本达到了收敛,如图 7所示.各个智能体之间相互协作,较好地完成了使网络效用最大化的任务.
|
图 5 时延随训练周期的变化 |

|
图 6 每个智能体的奖励值随周期的变化 |
|
图 7 奖励值总和随周期的变化 |
2) 不同算法性能比较
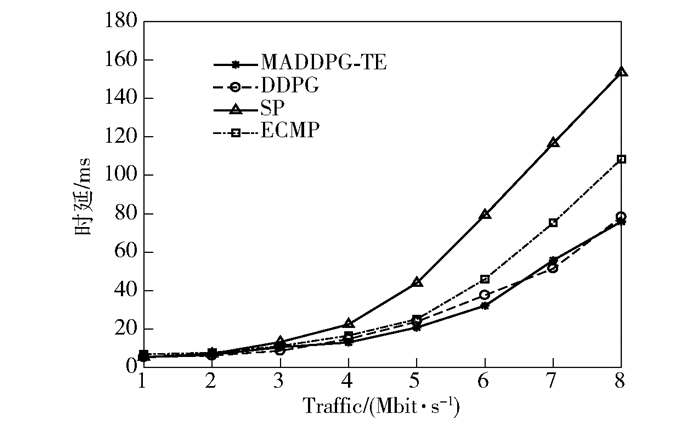
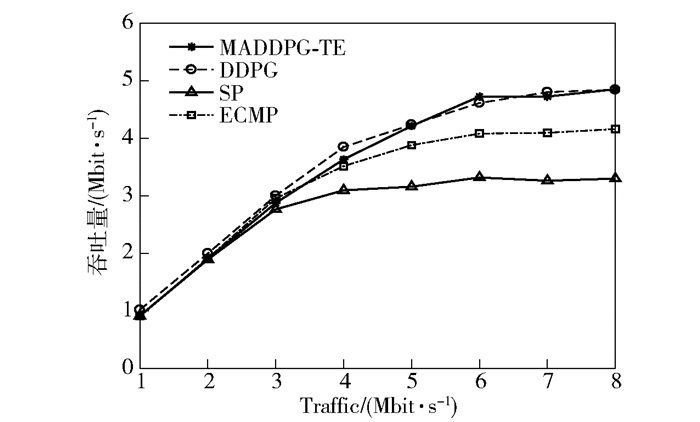
实验对比了最短路径(SP,shortest-path),多路径等价路由(ECMP, equal-cost multi-path)以及集中式的DDPG算法.流量需求从1~8 Mbit/s变化如图 8和图 9所示. MADDPG-TE算法相对于SP和ECMP算法,在高负载情况下,时延分别减少了53.7%和25.7%.吞吐量分别增长了29.5%和14.1%. MADDPG-TE算法跟DDPG效果在本实验中基本一致,都起到了较好的效果.由于MADDPG-TE是集中式训练,分布式执行的,其可以部署到网络边缘,在训练完成之后,可以由边缘节点去执行流量分配策略,可以认为这是一种源路由.
|
图 8 不同算法的端到端时延 |
|
图 9 不同算法的吞吐量对比 |
实验还单独对DDPG算法和MADDPG-TE算法的训练过程(Traffic为8 Mbit/s)中时延和吞吐量变化进行了比较,如图 10所示. MADDPG-TE和DDPG算法可以达到比较接近的结果,由于MADDPG-TE算法在做出动作决策的时候只会使用局部信息,所以相对DDPG算法MADDPG-TE算法抖动性稍大.但是在时延要求较高的网络环境中,控制信令等在SDN控制器和交换机的时延往往不能忽略,这时候该算法的有非常显著的优势. MADDPG-TE算法在训练好之后,只需要局部的观测信息就可以做出决策,减少了和控制器之间的交互时延.另外在SDN控制器发生故障时,MADDPG-TE算法也可以保持较好的效果.

|
图 10 MADDPG-TE和DDPG训练过程对比 |
以最大化网络效用函数为目的,提出了基于多智能体强化学习的流量分配策略.首先基于SDN提出一种新型智能网络架构,其核心是智能决策层;然后对强化学习中状态空间、行为空间和每个智能体的奖励值函数进行了设计,随后在智能决策层部署了MADDPG-TE算法,利用K-Shortest算法计算出的路径作为预计算的路径集合,搭建仿真环境并利用仿真环境进行实验分析,结果证明,该算法可以有效地在路径上进行流量分配,以达到网络效用最大的效果.与其他方法相比,该算法可以集中训练,分布式执行,保证性能的同时降低了控制器的压力.下一步将基于真实网络环境进行测试,以提高应用价值.
| [1] |
Agarwal S, Kodialam M, Lakshman T V. Traffic engineering in software defined networks[C]//2013 Proceedings IEEE INFOCOM. Turin, Italy: IEEE Press, 2013: 2211-2219.
|
| [2] |
Silver D, Huang A, Maddison C J, et al. Mastering the game of go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 |
| [3] |
Mestres A, Hibbett M J, Estrada G, et al. Knowledge-defined networking[J]. ACM SIGCOMM Computer Communication Review, 2017, 47(3): 2-10. DOI:10.1145/3138808.3138810 |
| [4] |
Chavula J, Densmore M, Suleman H. Using SDN and reinforcement learning for traffic engineering in UbuntuNet Alliance[C]//2016 International Conference on Advances in Computing and Communication Engineering (ICACCE). Durban, South Africa: IEEE Press, 2016: 349-355.
|
| [5] |
Xu Zhiyuan, Tang Jian, Meng Jingsong, et al. Experience-driven networking: a deep reinforcement learning based approach[C]//IEEE INFOCOM 2018-IEEE Conference on Computer Communications. Honolulu, USA: IEEE Press, 2018: 1871-1879.
|
| [6] |
Sutton R S, Barto A G. Reinforcement learning:an introduction[M]. Cambrige: MIT Press, 1998.
|
| [7] |
Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[EB/OL]. 2013(2013-12-19)[2019-07-05]. https://arxiv.org/pdf/1312.5602.pdf.
|
| [8] |
Lillicrap T P, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning[C]//Advances in Neural Information Processing Systems. Long Beach, USA: Curran Associates, 2017: 486-496.
|
| [9] |
Lowe R, Wu Y, Tamar A, et al. Multi-agent-actor-critic for mixed cooperative-competitive environments[C]//Advances in Neural Information Processing Systems. Long Beach, USA: Curran Associates, 2017: 6379-6390.
|
| [10] |
Winstein K, Balakrishnan H. Tcp ex machina: Computer-generated congestion control[C]//ACM SIGCOMM 2013. Hong Kong, China: ACM Press, 2013: 123-134.
|
| [11] |
张峰, 李刚, 宋丽. 一种适应网络拥塞的网络端到端时延估算模型[J]. 空军雷达学院学报, 2009, 23(3): 190-193. Zhang Feng, Li Gang, Song Li. An estimation model of end-to-end delay of network congestion[J]. Journal of Air Force Radar Academy, 2009, 23(3): 190-193. |



