媒介调制(MBM, media based modulation)是一种新提出的调制技术，与传统的相移键控(PSK, phase shift keying)、正交振幅调制(QAM, quadrature amplitude modulation)等不同，媒介调制通过扰动发射天线附近的传输环境，使无线信道随机变化，从而引起不同的衰落特性来携带不同信息，它能够在不增加发射能耗的前提下提高频谱利用率，有望成为下一代通信系统关键技术^[1-2].

Adejumobi等^[3]提出了基于媒介调制的空间调制(SMBM, spatial modulation-media based modulation)系统，它将空间调制(SM, spatial modulation)与MBM相结合，应用于多输入多输出(MIMO, multiple input multiple output)系统，发射天线与射频(RF, radio frequency)镜同时被索引，提高了系统的频谱效率.可是，SM技术在一个特定时间内只激活一根发射天线，其传输效率与发射天线数目成对数关系^[4]，传输效率仍然较低. Naresh等^[5]提出了基于媒介调制的广义空间调制(GSM-MBM, generalized spatial modulation-media based modulation).广义空间调制(GSM, generalized spatial modulation)的突出特点是拓展了SM的空间域概念，可同时激活多根发射天线用于发射信号.因此，在配置相同数目的发射天线时，GSM-MBM系统能获得比SMBM系统更高的频谱效率^[6].然而，GSM-MBM系统中激活发射天线组合(TAC, transmit antenna combination)与镜像激活模式组合(MAPC, mirror activation pattern combination)同时被索引，星座的维度大幅度增加，而且随着TAC和MAPC的增加，接收端的计算复杂度呈指数级上升，使得设备复杂度和成本大幅度增加.

基于上述背景，提出了一种基于能量排序下的松弛迭代(EO-RIM, energy ordered-relaxation iteration method)思想的低复杂度检测算法.该算法借鉴了文献[7]中GSM系统下基于有序块的最小均方误差(OB-MMSE, ordered block minimum mean squared error)检测算法的思想，但是，OB-MMSE算法中通过复杂的矩阵求逆运算来估计相应的调制符号向量，其计算复杂度随着发射天线数目呈立方增长.而EO-RIM算法对OB-MMSE检测算法进行了改进，利用松弛迭代运算来估计相应的调制符号向量，使计算复杂度随着激活天线的立方增长降低为平方增长，在基本不影响误码率(BER, bit-error ratio)性能的情况下，可进一步降低复杂度.并且，通过调整EO-RIM检测算法的阈值系数可得到系统性能与复杂度的折中.为了使EO-RIM算法更好地应用于未来实际通信场景，将提出的算法与低密度奇偶校验码(LDPC, low-density parity check codes)相结合，并验证误码率性能.

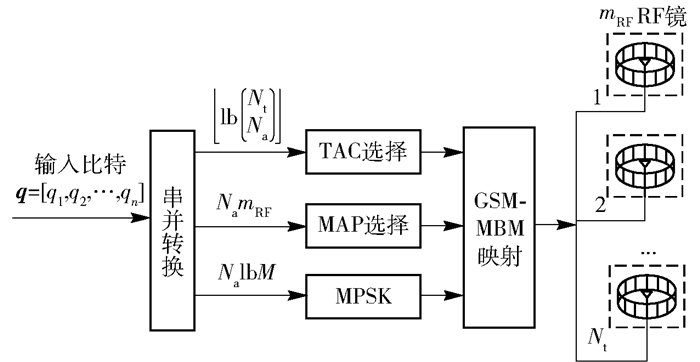
1 系统模型

GSM-MBM系统发射端模型如图 1所示，q=[q₁, q₂, …, q_n]表示输入比特，N_t表示发射天线，N_r表示接收天线.每根天线周围有m_RF个RF镜，通过输入比特‘1’或‘0’分别控制RF镜的开或关，从而扰动发送天线附近的传输环境来随机化无线信道，进而改变整个传输路径.因此，对于一根天线，可由附近的m_RF个RF镜产生N_m=2^m_RF种信道状态，而由m_RF个信息比特来控制RF镜的一种开关状态叫做“镜像激活模式(MAP, mirror activation pattern)”.对于一组激活的发射天线，可通过信息比特控制每根发射天线对应的镜像激活模式，由此得到的一组镜像激活模式叫做“镜像激活模式组合”.

从图 1中可以看出，信息比特通过3种方式传输：①从N_t个发射天线中选择N_a个用来传输$\left\lfloor \text{lb}\left( \begin{array}{*{35}{l}} {{N}_{\text{t}}} \\ {{N}_{\text{a}}} \\ \end{array} \right) \right\rfloor $，其中$\left(\begin{array}{l} N_{\mathrm{t}} \\ N_{\mathrm{a}} \end{array}\right) $表示从N_t个发射天线中激活N_a个的组合数，1≤N_a≤N_t，$ \left\lfloor \cdot \right\rfloor $表示向下取整，$\left( \begin{matrix} \cdot \\ \cdot \\ \end{matrix} \right) $表示二项式系数；②每个激活的发射天线中的m_RF个RF镜的开/关状态由m_RF比特信息位控制，一共可以传输N_am_RF比特信息；③每个激活的发射天线发送调制符号(MQAM或者MPSK)，共传输N_albM比特信息.系统频谱利用率可以表示为

$ \eta = \left\lfloor {{\rm{lb}}\left( {\begin{array}{*{20}{l}} {{N_{\rm{t}}}}\\ {{N_{\rm{a}}}} \end{array}} \right)} \right\rfloor + {N_{\rm{a}}}{m_{{\rm{RF}}}} + {N_{\rm{a}}}{\rm{lb}}M $

(1)

发射向量经过瑞利信道后，接收端接收到的信息为

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Hx}} + \mathit{\boldsymbol{n}} $

(2)

其中：y∈$\mathbb{C} $^N_r×1为接收向量；H∈$\mathbb{C} $^{N_r×(N_m×N_t)}为信道矩阵；n∈$\mathbb{C} $^N_r×1为高斯噪声矩阵，其元素服从均值为0、方差为σ²的复高斯分布. x∈$\mathbb{C} $^{(N_m×N_t)×1}为GSM-MBM调制端产生的发送向量，一般形式为

$ \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} 0& \cdots &0&{\left| {\underbrace {\begin{array}{*{20}{c}} 0& \cdots &{\mathop \downarrow \limits_{{s_1}}^{{k_1}} }& \cdots &0 \end{array}}_{天线\;{j_1}}} \right| \cdots \left| {\underbrace {\begin{array}{*{20}{c}} 0& \cdots &{\mathop \downarrow \limits_{{s_{_{{N_{\rm{a}}}}}}}^{{k_{{N_{\rm{a}}}}}} }& \cdots &0 \end{array}}_{天线\;{j_{_{{N_{\rm{a}}}}}}}} \right|}&0& \cdots &0 \end{array}} \right]^{\rm{T}}} $

(3)

其中：s₁, s₂, …, s_Na∈S表示PSK调制符号，而s₁, s₂, …, s_Na在x向量中的位置j₁, j₂, …, j_Na与激活的天线位置有关，即激活发射天线组合为{j₁, j₂, …, j_Na}，j₁, j₂, …, j_Na∈{1, 2, …, N_t}；k₁, k₂, …, k_Na则表示发射天线分别激活第k₁, k₂, …, k_Na个MAP，即镜像激活模式组合为{k₁, k₂, …, k_Na}，k₁, k₂, …, k_Na∈{1, 2, …, N_m}；x向量中非零符号的个数为N_a.

接收端采用最大似然检测，通过遍历搜索GSM-MBM接收向量的所有候选值，找到与接收向量欧式距离最小的星座点，从中恢复出信息比特，表达式为

$ \mathit{\boldsymbol{\hat x}} = \mathop {\arg \min }\limits_{\mathit{\boldsymbol{x}} \in {\mathit{\boldsymbol{S}}_{{\rm{GSM - MBM}}}}} {\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Hx}}} \right\|^2} $

(4)

其中：S_GSM-MBM表示GSM-MBM系统所有候选值的集合，S_GSM-MBM的大小，即最大似然(ML, maximum likelihood)检测算法的搜索空间为${{2}^{\left\lfloor \text{lb}\left( \begin{array}{*{35}{l}} {{N}_{\text{t}}} \\ {{N}_{\text{a}}} \\ \end{array} \right) \right\rfloor }}N_{m}^{{{N}_{\text{a}}}}{{M}^{{{N}_{\text{a}}}}} $，由此可见，ML检测算法的搜索复杂度随着激活天线数N_a呈指数级递增.

2 EO-RIM算法

为了减少最大似然检测的复杂度，提出了EO-RIM检测算法，其基本思想是：首先利用信道列向量对接收信号进行伪逆处理，并对TAC以及相应的MAPC(记作TAC-MAPC)下信号能量值进行排序，接着对于有序的TAC-MAPC，通过松弛迭代运算检测相应的调制符号向量，并通过预设阈值V_th来平衡误码率性能和检测复杂度之间的关系.算法包括以下3个步骤.

步骤1   GSM-MBM系统的信道矩阵H可表示为H=[H¹  H²  …  H^j  …  H^N_t]∈$\mathbb{C} $^{N_r×(N_m×N_t)}，H^j∈$\mathbb{C} $^N_r×N_m表示第j个发射天线到接收天线的信道矩阵，其中j∈{1, 2, …, N_t}.分别用H^j的列向量对接收向量y进行预处理，可得到恢复符号向量z^j∈$\mathbb{C} $^N_m×1，其元素为

$ z_k^j = \left( {\frac{{{{\left( {\mathit{\boldsymbol{h}}_k^j} \right)}^{\rm{H}}}}}{{{{\left( {\mathit{\boldsymbol{h}}_k^j} \right)}^{\rm{H}}}\mathit{\boldsymbol{h}}_k^j}}} \right)\mathit{\boldsymbol{y}} $

(5)

其中：h_k^j∈$\mathbb{C} $^N_r×1为H^j的第k∈{1, 2, …, N_m}列，表示接收天线与第k种镜像激活模式的信道增益.最终可得到恢复信号矩阵

$ \mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{z}}^1}}&{{\mathit{\boldsymbol{z}}^2}}& \cdots &{{\mathit{\boldsymbol{z}}^j}}& \cdots &{{\mathit{\boldsymbol{z}}^{{N_{\text{t}}}}}} \end{array}} \right] \in {\mathbb{C}^{{N_m} \times {N_{\text{t}}}}} $

计算恢复信号矩阵Z中每一个元素的能量，可得到$\boldsymbol{\bar{Z}}=\left[\begin{array}{llllll} \boldsymbol{\bar{z}}^{1} & \boldsymbol{\bar{z}}^{2} & \cdots & \boldsymbol{\bar{z}}^{j} & \cdots & \boldsymbol{\bar{z}}^{N_\text{t}} \end{array}\right] \in \mathbb{R}^{N_{m} \times N_\text{t}} $，其元素为

$ \bar z_k^j = {\left| {z_k^j} \right|^2} $

(6)

将所有可能的TAC-MAPC激活可能性用权值向量w=[w₁, w₂, …, w_N]^T表示，其元素为

$ {w_i} = \bar z_{i,{k_1}}^{{j_1}} + \bar z_{i,{k_2}}^{{j_2}} + \cdots + \bar z_{i,{k_{{N_{\rm{a}}}}}}^{{j_{{N_{\rm{a}}}}}} = \sum\limits_{n = 1}^{{N_{\rm{a}}}} {\bar z_{i,{k_n}}^{{j_n}}} $

(7)

其中i∈{1, 2, …, N}为TAC-MAPC的索引值，N= $2^{\left\lfloor \text{lb}\left( \begin{array}{*{35}{l}} {{N}_{\text{t}}} \\ {{N}_{\text{a}}} \\ \end{array} \right) \right\rfloor }\times N_m^{{N_{\rm{a}}}} $.集合A_i^j={j₁, j₂, …, j_Na}为激活的天线组合，其中j₁, j₂, …, j_Na∈{1, 2, …, N_t}；集合M_i^k={k₁, k₂, …, k_Na}表示激活发射天线所对应的镜像激活模式，其中k₁, k₂, …, k_Na∈{1, 2, …, N_m}，z_{i, kNa}^j_Na为Z中第j_Na列、第k_Na行元素.

对得到的权值向量w=[w₁, w₂, …, w_N]^T中的元素进行排序，可得到有序的TAC-MAPC

$ \begin{array}{*{20}{c}} {\left[ {\left( {A_{{i_1}}^j,M_{{i_1}}^k} \right),\left( {A_{{i_2}}^j,M_{{i_2}}^k} \right), \cdots ,\left( {A_{{i_N}}^j,M_{{i_N}}^k} \right)} \right] = }\\ {\arg \;{\rm{sort}}\left( \mathit{\boldsymbol{w}} \right)} \end{array} $

(8)

其中：sort(·)定义用于按降序对输入向量的元素进行重新排序的排序函数，并且i₁、i_N分别是w中最大值和最小值的索引，i₁, i₂, …, i_N∈{1, 2, …, N}.

步骤2  对于排序后的第m∈{1, 2，…, N}个TAC-MAPC，其对应的信道子矩阵H_m∈$\mathbb{C} $^N_r×N_a为

$ {\mathit{\boldsymbol{H}}_m} = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{h}}_{m,{k_1}}^{{j_1}}}&{\mathit{\boldsymbol{h}}_{m,{k_2}}^{{j_2}}}& \cdots &{\mathit{\boldsymbol{h}}_{m,{k_{{N_{\rm{a}}}}}}^{{j_{{N_{\rm{a}}}}}}} \end{array}} \right] $

(9)

其中：h_{m, kNa}^j_Na为H^j_Na的第k_Na∈{1, 2, …, N_m}列，表示接收天线与第j_Na个发射天线的第k_Na种镜像激活模式的信道增益.

文献[7]中提出了用最小均方误差算法估计调制符号向量，如

$ {{\mathit{\boldsymbol{\tilde s}}}_m} = Q\left( {{{\left( {{{\left( {{\mathit{\boldsymbol{H}}_m}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{H}}_m} + {\sigma ^2}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}{{\left( {{\mathit{\boldsymbol{H}}_m}} \right)}^{\rm{H}}}\mathit{\boldsymbol{y}}} \right) $

(10)

其中：I为N_a×N_a维单位矩阵，Q(·)表示数字解调处理.但该算法引入了复杂的矩阵求逆运算，计算复杂度随N_a呈立方增长.

为了降低求解逆矩阵带来的复杂度，提出采用松弛迭代法来估计调制符号向量$ {\mathit{\boldsymbol{\tilde s}}_m}$.估计相应的恢复符号向量$\hat{\boldsymbol{s}}_{m} \in \mathbb{C}^{N_{\mathrm{a}} \times 1} $，其可以写为

$ {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}}_m} = {\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{y}}_{{\rm{MF}}}} $

(11)

其中R=(H_m)^HH_m+σ²I，y_MF=(H_m)^Hy.对式(11)进行转换，可得到

$ \mathit{\boldsymbol{R}} \times {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}}_m} = {\mathit{\boldsymbol{y}}_{{\rm{MF}}}} $

(12)

从式(12)可以看出，矩阵求逆问题转换为求解线性方程的问题，${{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}}_m} $为待求解向量.将R分解为R=D－L－U，其中D、－L、－U分别为R的对角矩阵、严格下三角矩阵、严格上三角矩阵.则求解式(12)的松弛迭代法为^[8]

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}_m^{\left( {t + 1} \right)} = {{\left( {\mathit{\boldsymbol{\omega D}} - {\mathit{\boldsymbol{L}}^{\rm{H}}}} \right)}^{ - 1}}\left[ {\left( {\omega - 1} \right){\mathit{\boldsymbol{L}}^{\rm{H}}} + \omega \mathit{\boldsymbol{L}}} \right]\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}_m^{\left( t \right)} + }\\ {{{\left( {\mathit{\boldsymbol{D}} - \frac{1}{\omega }{\mathit{\boldsymbol{L}}^{\rm{H}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{y}}_{{\rm{MF}}}}} \end{array} $

(13)

其中ω为松弛因子，一般选为0 < ω < 2，t表示迭代次数，${{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}}_m} $是N_a×1维零向量.松弛迭代算法的收敛速度与松弛因子有关，通过改变ω的大小，可以得到不同的迭代次数，使算法复杂度与性能之间得到折中.根据式(13)得到的恢复符号向量${{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}}_m} $，对其进行解调处理，即可得到调制符号向量${{\mathit{\boldsymbol{\tilde s}}}_m} $

$ {{\mathit{\boldsymbol{\tilde s}}}_m} = Q\left( {{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }}}_m}} \right) $

(14)

式(13)中的ωD－L^H为三角矩阵，与式(10)相比，求解其逆矩阵的计算复杂度降为随N_a呈平方增长.

步骤3  若估计得到的调制符号向量${{\mathit{\boldsymbol{\tilde s}}}_m} $与发射符号向量s一致，归一化的ML代价因子可表示为ε=‖y－H_m${{\mathit{\boldsymbol{\tilde s}}}_m} $‖²/σ²，服从自由度为N_r，均值也为N_r的卡方分布；若估计得到的向量与发射向量不一致，则ε服从自由度为N_r的非中心卡方分布，其非中心参数为γ=‖H_m(s－ ${{\mathit{\boldsymbol{\tilde s}}}_m} $)‖²/σ²，均值为N_r+γ.若使$ {{\mathit{\boldsymbol{\tilde s}}}_m}$与s相等求得的概率比其他误判的情况概率高，根据卡方分布的特性，最优检测结果需要满足$\left\|\boldsymbol{y}-\boldsymbol{H}_{m} \tilde{\boldsymbol{s}}_{m}\right\|_{\mathrm{F}}^{2} < N_{\mathrm{r}} {\sigma}^{2} $.为了避免遍历所有TAC-MAPC产生的复杂度，可设置阈值V_th=cN_rσ².

当检测得到的(A_m^j, M_m^k, $ {{\mathit{\boldsymbol{\tilde s}}}_m}$)满足下式

$ {d_m} = \left\| {\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{H}}_m}{{\mathit{\boldsymbol{\tilde s}}}_m}} \right\|_{\rm{F}}^2 \le {V_{{\rm{th}}}} $

(15)

则终止检测，估计的激活发射天线组合为$\hat{A}^{j}=A_{m}^{j} $，其对应的镜像激活模式组合$\hat{M}^{k}=M_{m}^{k} $，检测得到的发射符号向量为$ \hat{\boldsymbol{s}}=\tilde{\boldsymbol{s}}_{m}$.若不满足式(15), 则继续进行(A_m+1^j, M_m+1^k)的检测.当m+1>N时，则选择最优估计(A_m^j, M_m^k, $ {{\mathit{\boldsymbol{\tilde s}}}_m}$)如下：

$ \left. {\begin{array}{*{20}{l}} {u = \arg \min \left\| {\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{H}}_m}{{\mathit{\boldsymbol{\tilde s}}}_m}} \right\|_{\rm{F}}^2,m \in \left\{ {1,2, \cdots ,N} \right\}}\\ {{{\hat A}^j} = A_u^j,{{\hat M}^k} = M_u^k,\mathit{\boldsymbol{\hat s}} = {{\mathit{\boldsymbol{\tilde s}}}_u}} \end{array}} \right\} $

(16)

通过调整阈值系数c，可灵活权衡系统的复杂度和误码率性能.

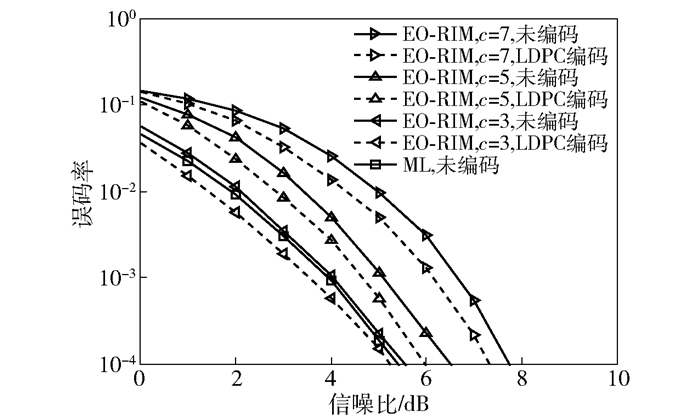
3 仿真结果与分析 3.1 仿真结果

下面通过计算机仿真了在ML算法、OB-MMSE算法以及EO-RIM算法下系统的误码率性能.假设信道为准静态平坦瑞利衰落信道，在N_r=16, N_t=4, N_a=2, N_m=4，调制方式为QPSK，改变阈值系数c时，ML检测算法、OB-MMSE算法以及EO-RIM算法在具有LDPC信道编码系统与未编码系统中的性能对比如图 2所示.其中，在LDPC信道编码系统中，码长为200 bit，码率为0.26.

从图 2可以看到，当预设阈值V_th的系数c=3时，未编码系统中EO-RIM算法的BER性能与ML检测算法相近，但是随着c的增大，EO-RIM算法性能逐渐变差.因为c值较大，意味着阈值V_th较大，检测的TAC-MAPC数目较少，错误概率增大.随着c的减小，阈值V_th减小，检测的TAC-MAPC数目增多，错误概率降低，但复杂度也随之增大.因此调整c的大小，可以得到系统性能与复杂度的折中. LDPC信道编码系统与未编码系统相比，在误码率达到10^-4时，性能提升了约0.5 dB.

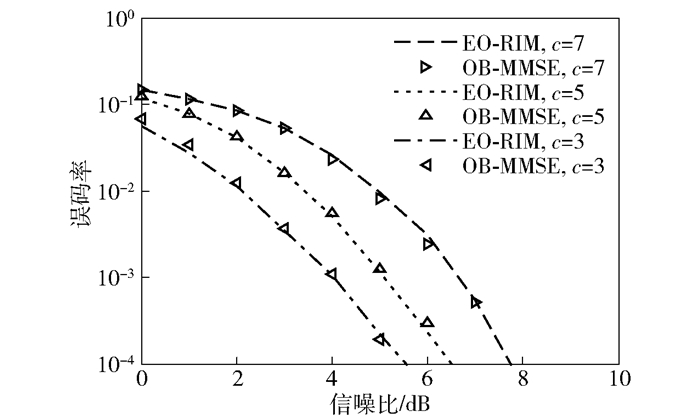
在同样参数环境下，比较了未编码系统中OB-MMSE和EO-RIM算法的性能，如图 3所示.可以看出，在不同阈值系数c时，EO-RIM算法性能几乎与OB-MMSE算法性能一致.

3.2 复杂度分析

为了分析GSM-MBM未编码系统的ML检测算法、OB-MMSE算法以及EO-RIM算法的计算复杂度，以算法中包含的乘法作为比较(除法也认定为乘法).复杂度分析如下：

1) ML检测算法

① 计算‖y－Hx‖²需要O(N_rN_a)次乘法计算；

② 最大似然搜索空间大小为$2^\left\lfloor \text{lb}\left( \begin{array}{*{35}{l}} {{N}_{\text{t}}} \\ {{N}_{\text{a}}} \\ \end{array} \right) \right\rfloor N_m^{{N_{\rm{a}}}}{M^{{N_{\rm{a}}}}} $，因此搜索所有星座点所需的乘法次数为O(N_rN_a)× $2^\left\lfloor \text{lb}\left( \begin{array}{*{35}{l}} {{N}_{\text{t}}} \\ {{N}_{\text{a}}} \\ \end{array} \right) \right\rfloor N_m^{{N_{\rm{a}}}}{M^{{N_{\rm{a}}}}} $.

2) OB-MMSE算法

① 对y进行预处理，并获得加权因子向量w，需要O(3N_rN_tN_m)次乘法运算；

② 通过块最小均方误差均衡处理方法检测第m个的TAC-MAPC，估计相应的调制符号向量${{\mathit{\boldsymbol{\tilde s}}}_m} $，需要$ O\left(2 N_{\mathrm{r}} N_{\mathrm{a}} N_{\mathrm{a}}+\frac{1}{3} N_{\mathrm{a}}^{3}\right)$次乘法运算；

③ 通过预设的阈值V_th进行判定，并求得d_m，需要O(N_rN_a)次乘法运算；

④ 式(10)中被检测的TAC-MAPC的平均数目为P_avg，则该检测算法的计算复杂度为O(3N_rN_tN_m)+ (O(2N_rN_aN_a+$\frac{1}{3} $N_a³)+O(N_rN_a)P_avg.

3) EO-RIM算法

① 对y进行预处理，并获得加权因子向量w，需要O(3N_rN_tN_m)次乘法运算；

② 对于第m个的TAC-MAPC，用松弛迭代法估计相应的调制符号向量${{\mathit{\boldsymbol{\tilde s}}}_m} $，需要O(N_rN_a+$\frac{{N_{\rm{a}}^2}}{2}t $)次运算，其中t为迭代次数；

③ 通过预设的阈值V_th进行判定，并求得d_m，需要O(N_rN_a)次乘法运算；

④ 检测TAC-MAPC组合的平均数目为P_avg，则该检测算法的计算复杂度为(O(3N_rN_tN_m)+O(N_rN_a+N_a²+$\frac{{N_{\rm{a}}^2}}{2}t $)+O(N_rN_a)P_avg.

图 4显示了在N_r=16, N_t=4, N_a=2, N_m=4，调制方式为QPSK，改变阈值系数c时，ML检测算法、OB-MMSE算法和EO-RIM算法的复杂度对比.从图中可以看出，ML检测算法的复杂度与阈值系数c无关，在c改变时保持不变.而OB-MMSE算法和EO-RIM算法的复杂度均随着阈值系数c的增大而递减.这是因为随着c的增大，预设阈值V_th增大，被检测的TAC-MAPC的平均数目P_avg减小，复杂度随之降低.与OB-MMSE算法相比，EO-RIM算法的复杂度较低，因为EO-RIM算法将OB-MMSE算法中复杂的矩阵求逆从随着N_a的立方增长降低为随着N_a的平方增长.

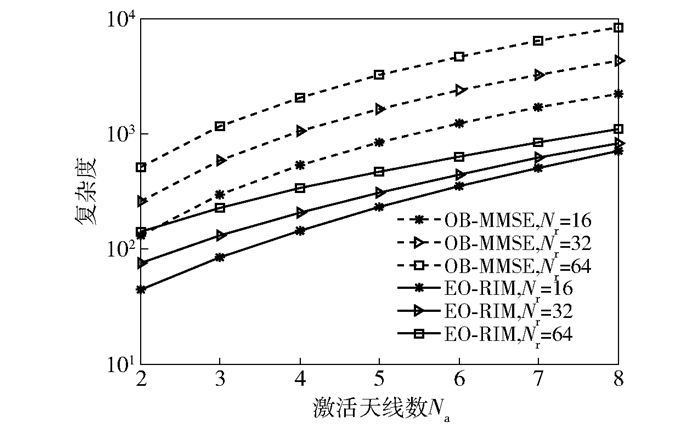
从复杂度分析可知，OB-MMSE和EO-RIM两种算法复杂度的不同主要体现在式(10)与式(13)的复杂度计算上，图 5显示了N_t=8, N_m=2，调制方式为QPSK时，2种算法在这一部分的复杂度对比.从图中可以看出，随着N_a的增大，OB-MMSE算法复杂度仍大幅度增长，而EO-RIM算法复杂度增长速度逐渐减缓.并且随着N_r的增大，EO-RIM算法复杂度相比OB-MMSE算法至少降低了50%.

4 结束语

针对GSM-MBM系统检测复杂度较高的问题，提出了EO-RIM算法.鉴于OB-MMSE算法中逆矩阵求解复杂度较高的问题，提出使用松弛迭代算法估计调制符号向量.性能仿真和复杂度分析结果表明，EO-RIM算法在基本不影响系统误码率性能的情况下可以有效降低接收端检测的复杂度，特别是在大规模发射天线和激活天线以及高阶调制等复杂系统下具有综合优势.将基于EO-RIM检测算法的GSM-MBM系统与LDPC信道编码相结合，误码率性能有所改善.下一步可以继续研究编码系统的检测算法，进一步改善误码率性能，更好地应用于未来实际通信场景.