针对改善波长转换器转换特性的问题,研究了周期极化铌酸锂晶体中采用分段准相位匹配光栅结构对基于级联和频+差频效应的波长转换器特性的影响.对于单通和双通构型,增加段数,并优化设计每段的极化周期,可以同时获得高转换效率、大转换带宽和较好的平坦性.在相同条件下,双通构型波长转换器的转换效率和平坦性较好,但转换带宽比单通构型稍差.与采用位移泵浦光的波长提高平坦性的方法相比,利用分段准相位匹配光栅结构能够获得几乎相同的平坦性,但转换效率和转换带宽却比泵浦光波长位移法好.此外,研究了晶体长度对基于分段准相位匹配光栅结构波长转换器特性的影响.
In order to improve the conversion characteristics of wavelength converters, the effect of the segmented quasi-phase matched grating structure in the periodically poled lithium niobate crystal on the characteristics of wavelength converters based on cascaded sum + difference frequency generation is studied. For both of single-pass and double-pass configurations, high conversion efficiency, large conversion bandwidth, and good flatness can be achieved simultaneously by increasing the number of segments and optimizing the poling period of each segment. Under the same conditions, the conversion efficiency and flatness of the double-pass configuration are better, but the conversion bandwidth is slightly worse than that of the single-pass configuration. Compared with the method of shifting the wavelength of one of the pump light, the use of segmented quasi-phase matched grating structure in wavelength converter can obtain almost the same flatness but better conversion efficiency and conversion bandwidth. Moreover, the effect of crystal length on the characteristics of a wavelength converter based on the segmented quasi-phase matched grating structure is also investigated.
全光波长转换技术是波分复用全光网络中提供波长路由和波长再利用的关键技术[1-3].目前,已有多种不同的技术用来实现全光波长转换,其中基于准相位匹配(QPM, quasi-phase matching)技术的全光波长转换器由于具有对调制格式全透明、响应速度快、无啁啾等优点,引起了研究者们的广泛关注[4-7].最初的QPM结构大都采用均匀极化周期,可以利用不同的二阶非线性效应及构型来实现全光波长转换,但整体而言,转换带宽都较小.级联和频(SFG, sum frequency generation)+差频(DFG, difference frequency generation)二阶非线性效应使用2个泵浦源产生DFG所需780 nm泵浦光,因此与其他的二阶非线性效应相比,其对单个泵浦源的功率要求减小了,另外也可以通过调整2个泵浦源的功率或它们之间的波长间隔来改善波长转换特性.研究结果表明,通过适当位移级联SFG+DFG效应波长转换器中的一束泵浦光的波长,可以有效改善转换效率曲线的平坦性,但与位移前相比转换带宽却变小了,转换效率也有所下降[8-9]. Tehranchi等[10-11]提出了步变啁啾光栅结构,用来提高转换效率曲线的平坦性,但是其转换带宽仍然较小,不足100 nm.
为了同时获得高平坦性、大转换带宽和高转换效率,利用分段准相位匹配光栅结构对基于级联SFG+DFG效应的波长转换过程进行了研究,通过优化设计每一段光栅结构的极化周期,不仅可获得与泵浦光波长位移法几乎相同的平坦性,并且转换带宽也得到了较大的扩展,转换效率也优于泵浦光波长位移法.随着所分段数的增加,虽然平坦性和转换效率稍有下降,但转换带宽却越来越大.同时还研究了晶体长度对波长转换特性的影响,结果表明,随着晶体长度的增加,转换带宽逐渐减小,但转换效率却不断增大,平坦性也有改善.
1 原理和模型在传统的基于均匀极化周期QPM晶体和级联SFG+DFG效应的波长转换过程中,极化周期通常被设计成令SFG满足相位匹配以获得较高的转换效率[12-13].但此时远离泵浦光波长位置处后相位失配将变大,导致转换效率快速下降,从而使得转换带宽较小,转换效率曲线的平坦性也较差.为了提高平坦性,并同时获得大转换带宽和较高的转换效率,可以对传统均匀极化周期QPM晶体的结构进行改变,采用分段准相位匹配光栅结构,如图 1所示.

|
图 1 分段准相位匹配光栅结构 |
利用QPM晶体中的周期极化铌酸锂(PPLN, periodically poled lithium niobate)晶体,将长度为L的PPLN晶体沿着光的传输方向(x轴)分成m段,每段都有一个统一的极化周期Λt(t∈[1, m]).当确定泵浦光和信号光的波长后,每段晶体中的相位失配因子Δkt会随着Λt值的变化而变化,因而在每段晶体内发生SFG和DFG过程的相互作用光波并不能完全的相位匹配,这会导致两束泵浦光附近的转换效率下降,但离泵浦光波长稍远位置处的转换效率却可以得到改善,从而使得转换效率曲线的顶部变平坦,转换带宽也相应的得到扩展.此外,随着所分段数的增加,相位失配因子Δkt随之增加,此时带宽的扩展效果变好,但相应的转换效率和平坦性会变差.因此,实际中可以通过综合考虑对转换效率、转换带宽和平坦性的要求以及设备制造的复杂性,选择合适的段数,并通过优化设计每段的Λt来获得平坦、宽带、高效的波长转换器.
基于级联SFG+DFG效应的波长转换器,根据和频光在晶体内的传输次数,可以分为单通和双通2种构型.
1) 单通构型
在单通构型级联SFG+DFG波长转换过程中,SFG与DFG过程同时进行,和频光在晶体内只传播一次.首先,两束频率分别为ωp1和ωp2的泵浦光与频率为ωs的信号光同时从晶体的一侧进入,两束泵浦光发生SFG作用产生频率为ωSF=ωp1+ωp2的和频光,随后新生成的和频光又与信号光发生DFG作用,产生频率为ωc=ωSF-ωs的转换光.上述过程可用如下的耦合波方程表述:
| $ \frac{\partial E_{p1 }}{\partial x}=-\mathrm{i} \omega_{p1} k_{\mathrm{SF}} E_{p 2}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{SF}} x\right)-\frac{\alpha_{p 1}}{2} E_{p1} $ | (1a) |
| $ \frac{\partial E_{p_{2}}}{\partial x}=-\mathrm{i} \omega_{p 2} k_{\mathrm{SF}} E_{p 1}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{SF}} x\right)-\frac{\alpha_{p 2}}{2} E_{p 2} $ | (1b) |
| $ \frac{\partial E_{s}}{\partial x}=-\mathrm{i} \omega_{s} k_{\mathrm{DF}} E_{c}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{DF}} x\right)-\frac{\alpha_{s}}{2} E_{s} $ | (1c) |
| $ \frac{\partial E_{c}}{\partial x}=-\mathrm{i} \omega_{c} k_{\mathrm{DF}} E_{s}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{DF}} x\right)-\frac{\alpha_{c}}{2} E_{c} $ | (1d) |
| $ \begin{array}{c} \frac{\partial E_{\mathrm{SF}}}{\partial x}=-\mathrm{i} \omega_{\mathrm{SF}} k_{\mathrm{SF}} E_{p 1} E_{p 2} \exp \left(\mathrm{i} \Delta k_{\mathrm{SF}} x\right)- \\ \mathrm{i} \omega_{\mathrm{SF}} k_{\mathrm{DF}} E_{s} E_{c} \exp \left(\mathrm{i} \Delta k_{\mathrm{DF}} x\right)-\frac{\alpha_{\mathrm{SF}}}{2} E_{\mathrm{SF}} \end{array} $ | (1e) |
其中:E为场分布,α为传输损耗,ΔkSF与ΔkDF分别为SFG和DFG过程的相位失配因子,定义为
| $ \begin{aligned} &\Delta k_{\mathrm{SF}}=k_{\mathrm{SF}}-k_{p 1}-k_{p 2}-k_{\mathit{\Lambda}}=\\ &2 \mathtt{π}\left(\frac{n_{\mathrm{SF}}}{\lambda_{\mathrm{SF}}}-\frac{n_{p 1}}{\lambda_{p 1}}-\frac{n_{p 2}}{\lambda_{p 2}}-\frac{1}{\mathit{\Lambda}}\right) \end{aligned} $ | (2a) |
| $ \begin{aligned} &\Delta k_{\mathrm{DF}}=k_{\mathrm{SF}}-k_{s}-k_{c}-k_{\mathit{\Lambda}}=\\ &2 \mathtt{π}\left(\frac{n_{\mathrm{SF}}}{\lambda_{\mathrm{SF}}}-\frac{n_{s}}{\lambda_{s}}-\frac{n_{c}}{\lambda_{c}}-\frac{1}{\mathit{\Lambda}}\right) \end{aligned} $ | (2b) |
其中:k为耦合系数,n为折射率,λ为波长,下标p1和p2、s、c分别代表泵浦光1和2、信号光和转换光,下标SF和DF分别代表和频光与差频光,Λ为极化周期.当式(2)结果为0时,代表完全相位匹配,此时可以获得最大的转换效率.
2) 双通构型
在双通构型中,两束泵浦光和信号光分别从晶体的两侧进入,SFG过程只发生在前向(+x方向)传输过程中,在反向(-x方向)传输过程中发生DFG过程,这是2个独立的过程.与单通构型相比,双通构型中和频光在晶体内沿着前向和反向传输了两次,晶体长度被有效利用,因此转换效率较高.
双通构型中SFG与DFG过程相对独立,因而可以将双通级联SFG+DFG效应的耦合波方程分为2部分,其中前向传输发生的SFG过程的耦合波方程为
| $ \frac{\partial E_{p 1}}{\partial x}=-\mathrm{i} \omega_{p 1} k_{\mathrm{SF}} E_{p 2}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{SF}} x\right)-\frac{\alpha_{p 1}}{2} E_{p 1} $ | (3a) |
| $ \frac{\partial E_{p 2}}{\partial x}=-\mathrm{i} \omega_{p 2} k_{\mathrm{SF}} E_{p 1}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{SF}} x\right)-\frac{\alpha_{p 2}}{2} E_{p 2} $ | (3b) |
| $ \frac{\partial E_{\mathrm{SF}}}{\partial x}=-\mathrm{i} \omega_{\mathrm{SF}} k_{\mathrm{SF}} E_{p 1} E_{p 2} \exp \left(\mathrm{i} \Delta k_{\mathrm{SF}} x\right)-\frac{\alpha_{\mathrm{SF}}}{2} E_{\mathrm{SF}} $ | (3c) |
在x = L处, 和频光被反射, 与此处入射的信号光一起反向传输, 发生DFG过程, 对应的耦合波方程为
| $ \frac{\partial E_{s}}{\partial x^{\prime}}=-\mathrm{i} \omega_{s} k_{\mathrm{DF}} E_{c}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{DF}} x^{\prime}\right)-\frac{\alpha_{s}}{2} E_{s} $ | (4a) |
| $ \frac{\partial E_{c}}{\partial x^{\prime}}=-\mathrm{i} \omega_{c} k_{\mathrm{DF}} E_{s}^{*} E_{\mathrm{SF}} \exp \left(-\mathrm{i} \Delta k_{\mathrm{DF}} x^{\prime}\right)-\frac{\alpha_{c}}{2} E_{c} $ | (4b) |
| $ \frac{\partial E_{\mathrm{SF}}}{\partial x^{\prime}}=-\mathrm{i} \omega_{\mathrm{SF}} k_{\mathrm{DF}} E_{s} E_{c} \exp \left(\mathrm{i} \Delta k_{\mathrm{DF}} x^{\prime}\right)-\frac{\alpha_{\mathrm{SF}}}{2} E_{\mathrm{SF}} $ | (4c) |
其中x′=L-x.
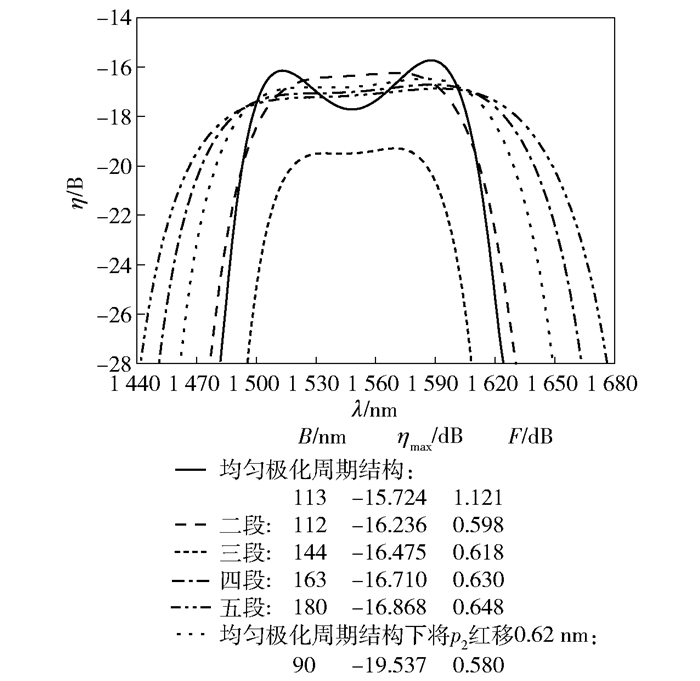
2 结果与分析为了获得高效、宽带、平坦的波长转换特性,利用图 1所示的分段准相位匹配光栅结构及耦合波方程(1)、(3)和(4),对基于单、双通级联SFG+DFG效应的波长转换器的特性进行了仿真研究.在仿真过程中,为了使均匀极化周期结构能够获得较大的转换带宽[13],两束泵浦光波长分别设置为1.512 5 μm与1.587 5 μm(间隔75 nm),它们的功率根据平衡条件[12, 14]分别设为25.605 mW和24.395 mW,信号光波长在1 440~1 690 nm范围内变化,功率为1 mW.在晶体长度L=3 cm,工作温度为150 ℃的条件下,当将晶体分别分为2~5段时并通过优化设计每一段的极化周期,得到单、双通构型下最终的转换效率曲线,分别如图 2和图 3所示,相应的极化周期如表 1所示.为了验证分段准相位匹配光栅结构的优越性,分别仿真了利用均匀极化周期结构和泵浦光波长位移法[8-9]对应的波长转换过程,结果分别如图 2和图 3中实线和短点虚线所示.为了描述转换效率的平坦性,定义平坦度F为[15]最大转换效率ηmax减去3 dB带宽内的平均转换效率ηmean.
|
图 2 单通构型下的转换效率曲线 |

|
图 3 双通构型下的转换效率曲线 |
|
|
表 1 不同准相位匹配光栅结构的极化周期分布 |
从图 2可以看出,与传统的均匀极化周期结构相比,采用分段准相位匹配光栅结构可以显著地扩展转换带宽并提高平坦度.例如,4段光栅结构与均匀极化周期结构相比,带宽B由113 nm扩展到了163 nm,平坦度F由1.121 dB改善为0.630 dB,非常平坦.虽然最大转换效率ηmax由-15.724 dB下降为-16.710 dB,但转换效率的下降可以在实际中通过提高输入泵浦光的功率得到补偿[16].泵浦光波长位移法是通过调节一束泵浦光的波长来打破式(2)对应的完全相位匹配条件,以牺牲转换效率和带宽来换取平坦性的提高.在利用此法[8-9]的仿真过程中,将泵浦光p2的波长向长波方向移动(红移),移动的距离为获得最好的平坦性时所对应的距离.通过研究,当泵浦光p2红移0.62 nm可以获得最好的平坦度,为0.580 dB,只比4段光栅结构的平坦度好了0.05 dB,优势不明显,但转换带宽却只有90 nm,最大转换效率也下降到了-19.537 dB.通过对比可以看出,分段准相位匹配光栅结构具有良好的综合波长转换特性,并且随着段数的增加,转换带宽越来越大,虽然相应的转换效率和平坦度都有所下降,但下降程度不大,且可以通过增加泵浦光功率来提高转换效率.因此,可以根据实际需求,通过采用不同的段数来获得自己所需的波长转换特性.
双通构型下的仿真结果如图 3所示.与单通构型类似,从图 3可以看出,在双通构型中,分段准相位匹配光栅结构与均匀极化周期结构相比具有更大的转换带宽和更好的平坦度,但最大转换效率稍差;与泵浦光波长位移法相比,分段准相位匹配光栅结构具有更大的转换带宽和较好的转换效率,且平坦度相差不大,即双通构型中分段准相位匹配光栅结构亦具有良好的综合波长转换特性.通过对比图 2和图 3可以发现,与单通构型相比,在相同的分段情况下,双通构型具有与单通构型几乎相同的平坦度和转换带宽,如同样采用4段QPM光栅结构,单、双通构型的平坦度和转换带宽分别为0.630 dB和0.629 dB及163 nm和161 nm;但双通构型的最大转换效率却比单通构型的好很多,4段准相位匹配光栅结构时分别为-10.843 dB和-16.710 dB,大了近6 dB.因此实际中推荐使用双通构型下的分段准相位匹配光栅结构以获得良好的波长转换特性.
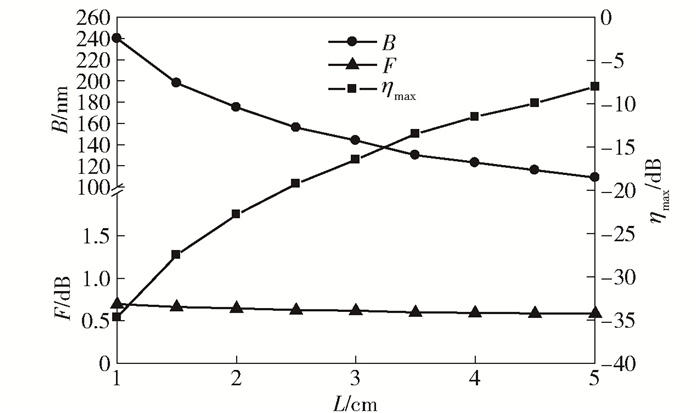
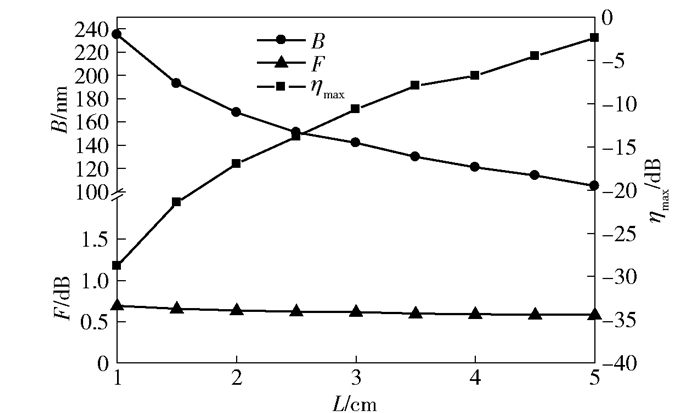
此外,对晶体长度对波长转换器特性的影响进行了研究.当将PPLN晶体分为3段光栅结构时,令其长度L从1 cm变化到5 cm,每隔0.5 cm做一次实验仿真,得到单、双通构型下的波长转换特性随晶体长度的变化结果,分别如图 4和图 5所示.从图 4和图 5可以看出,随着晶体长度的增加,单、双通构型下的最大转换效率都在不断增大,平坦性也有相应改善,但转换带宽却在逐渐降低.对于不同的晶体长度,双通构型对应的最大转换效率都明显优于单通构型,且转换带宽和平坦度几乎相同,与前面所得的结论一致.
|
图 4 单通构型中转换带宽、平坦度和最大转换效率随晶体长度的变化 |
|
图 5 双通构型中转换带宽、平坦度和最大转换效率随晶体长度的变化 |
根据以上所得结果,对利用分段准相位匹配光栅结构设计波长转换器提出了一些指导性建议.
1) 晶体长度的选择.虽然随着晶体长度的增加,转换效率不断地增大,平坦性也相应地改善,但后者的改善效果较小,且转换效率的增加效果也可以通过提高泵浦光功率来代替.而转换带宽却会随着晶体长度的增加快速地下降,且晶体制造的成本随之增加.因此,实际中使用3 cm长的晶体即可.
2) 所分段数的选择.随着段数的增加,转换带宽越来越大,转换效率和平坦度虽变差但下降程度不大.但由于3段时单/双通构型的转换带宽均已达到140 nm,覆盖了全部的C和L波段以及大部分的S波段,已可满足绝大多数光纤通信对带宽的要求.再考虑到段数继续提高后,晶体制造的复杂度和成本随之变大,所以实际中使用3段结构即可.
综上所述,实际中可以根据需求,通过采用双通构型分段准相位匹配光栅结构,并合理选择所分段数和晶体长度来获得不同的波长转换特性.但如果综合考虑转换效率、平坦度、转换带宽、晶体制造的复杂度和成本等因素,实际中推荐使用双通构型下3 cm长3段准相位匹配光栅结构.
3 结束语利用分段准相位匹配光栅结构对基于级联SFG+DFG效应的波长转换器的特性进行了研究.对于单通和双通构型,通过优化设计每段光栅结构的极化周期,可以获得比采用均匀极化周期结构更宽、更平坦的波长转化特性; 虽然转换效率稍差,但可以通过适当地增强泵浦光功率得到补偿.在相同条件下,与泵浦光波长位移法相比,利用分段准相位匹配光栅结构可以获得几乎相同的平坦性,但转换带宽却比前者大很多,且转换效率也较好.因此,利用分段准相位匹配光栅结构可以获得良好的综合波长转换特性.晶体长度对基于分段准相位匹配光栅结构波长转换器特性影响的研究结果表明,对于单、双通构型,随着晶体长度的增加,最大转换效率都在不断地增加,平坦性也有相应地改善,但转换带宽却在逐渐降低.相同晶体长度和相同段数条件下,双通构型可以获得与单通构型几乎相同的平坦性和转换带宽,但最大转换效率却明显优于单通构型.因此,实际中推荐使用双通构型下的分段准相位匹配光栅结构,并通过合理选择所分段数和晶体长度来获得想要的波长转换特性.
| [1] |
Tan H N, Inoue T, Solis-Trapala K, et al. On the cascadability of all-optical wavelength converter for high-order QAM formats[J]. Journal of Lightwave Technology, 2016, 34(13): 3194-3205. DOI:10.1109/JLT.2016.2545246 |
| [2] |
Naimi S, Duill S, Barry L. All optical wavelength of conversion of Nyquist-WDM superchannels using FWM in SOAs[J]. Journal of Lightwave Technology, 2015, 33(19): 3959-3967. DOI:10.1109/JLT.2015.2461021 |
| [3] |
Teng Xiang, Zhang Hanyi, Ya Bin. Improvement and development of all-optical wavelength conversion technologies[J]. Infrared & Laser Engineering, 2003, 32(2): 195-198. |
| [4] |
Tehranchi A, Morandotti R, Kashyap R. Efficient flattop ultra-wideband wavelength converters based on double-pass cascaded sum and difference frequency generation using engineered chirped gratings[J]. Optics Express, 2011, 19(23): 22528-22534. DOI:10.1364/OE.19.022528 |
| [5] |
Ishizuki H, Taira T. Quasi phase-matched quartz for intense-laser pumped wavelength conversion[J]. Optics Express, 2017, 25(3): 2369-2376. DOI:10.1364/OE.25.002369 |
| [6] |
罗勇锋, 陈云琳, 袁建伟, 等. 准相位匹配级联二阶非线性全光波长转换研究[J]. 光学学报, 2005, 25(5): 651-654. Luo Yongfeng, Chen Yunlin, Yuan Jianwei, et al. Study of quasi-phase matched cascaded χ(2) all-optical wavelength conversion[J]. Acta Optica Sinica, 2005, 25(5): 651-654. DOI:10.3321/j.issn:0253-2239.2005.05.017 |
| [7] |
Ahlawat M, Tehranchi A, Xu C Q, et al. Ultrabroadband flattop wavelength conversion based on cascaded sum frequency generation and difference frequency generation using pump detuning in quasi-phase-matched lithium niobate waveguides[J]. Applied Optics, 2011, 50(25): E108-E111. DOI:10.1364/AO.50.00E108 |
| [8] |
Gao S, Yang C, Xiao X, et al. Bandwidth enhancement and response flattening of cascaded sum- and difference-frequency generation-based wavelength conversion[J]. Optics Communications, 2006, 266(1): 296-301. |
| [9] |
Tehranchi A, Kashyap R. Efficient wavelength converters with flattop responses based on counter propagating cascaded SFG and DFG in low-loss QPM LiNbO3 waveguides[J]. Optics Express, 2009, 17(21): 19113-19119. DOI:10.1364/OE.17.019113 |
| [10] |
Tehranchi A, Kashyap R. Flattop efficient cascaded χ (SFG + DFG)-based wideband wavelength converters using step-chirped gratings[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2012, 18(2): 785-793. DOI:10.1109/JSTQE.2011.2136324 |
| [11] |
Tehranchi A, Kashyap R. Design of novel unapodized and apodized step-chirped quasi-phase matched gratings for broadband frequency converters based on second-harmonic generation[J]. Journal of Lightwave Technology, 2008, 26(3): 343-349. DOI:10.1109/JLT.2007.909862 |
| [12] |
Yu S, Gu W. Wavelength conversions in quasi-phase matched LiNbO3 waveguide based on double-pass cascaded χ(2) SFG+DFG interactions[J]. IEEE Journal of Quantum Electronics, 2004, 40(11): 1548-1554. DOI:10.1109/JQE.2004.835718 |
| [13] |
Chen B, Xu C Q. Analysis of novel cascaded χ(2) (SFG+DFG) wavelength conversions in quasi-phase-matched waveguides[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2004, 40(3): 256-261. DOI:10.1109/JQE.2003.823023 |
| [14] |
Yu S, Gu W. A tunable wavelength conversion and wavelength add/drop scheme based on cascaded second-order nonlinearity with double-pass configuration[J]. IEEE Journal of Quantum Electronics, 2005, 41(7): 1007-1012. DOI:10.1109/JQE.2005.848916 |
| [15] |
Liu T, Djordjevic I B, Song Z, et al. Broadband wavelength converters with flattop responses based on cascaded second-harmonic generation and difference frequency generation in Bessel-chirped gratings[J]. Optics Express, 2016, 24(10): 10946-10955. DOI:10.1364/OE.24.010946 |
| [16] |
卢嘉, 胡园园, 刘剑飞, 等. 基于SOA的平行双抽运结构偏振复用OFDM信号的全光波长变换[J]. 中国激光, 2015, 42(2): 159-166. Lu Jia, Hu Yuanyuan, Liu Jianfei, et al. All-optical wavelength conversion based on parallel dual-pump for polarization multiplexing OFDM signal in SOA[J]. Chinese Journal of Lasers, 2015, 42(2): 159-166. |


