针对在山区地形上非测距三维基于距离向量的定位算法存在定位误差较大的问题,提出了山区复杂地形的无线传感器网络节点定位算法(NLA-MT).该算法有效地利用了山区地形环境的特点,用局部平面拟合山区地形表面,并将三维空间定位运算降为二维平面的定位运算来进行节点定位,有效提高了节点的定位精度.不同通信半径、不同锚节点比例、不同节点总数的多角度仿真实验结果显示,NLA-MT定位算法在山区地形场景中表现良好,有效提高了无线传感器网络非测距定位算法精度.
Aiming at the problem that the non-ranging three-dimensional distance vector based localization algorithm has a large positioning error in mountainous terrain, a wireless sensor network node localization algorithm (NLA-MT) is proposed. The algorithm effectively utilizes the characteristics of the mountainous terrain environment and uses the local plane to fit the surface of the mountainous terrain. The three-dimensional spatial positioning operation is reduced to a two-dimensional plane positioning operation to perform node positioning, which effectively improves the positioning accuracy of the node. The multi-angle simulation experiments with different communication radius, different anchor node ratios and different total nodes show that the NLA-MT localization algorithm performs well in mountainous terrain scenes. The accuracy of the non-ranging positioning algorithm of the wireless sensor network is effectively improved.
无线传感器网络(WSN, wireless wensor network)的出现引起了全世界的广泛关注.无线传感器网络被列为当今世界最具影响的技术之一[1-2].无线传感器网络在环境监测与预报、森林防火、地质灾害监测与预警、城市交通、空间探索以及医疗健康监测等方面具有重要的应用前景.节点定位技术是WSN研究的热点之一[3-5]. WSN以无线通信方式构建的一个网络系统,用于感知、采集目标区域的信息并传送到监控中心.在环境监测中必需要知道事件源的发生地点,如必须要知道污染源发生的地点,森林火灾发生的地域等[6-7].没有位置信息的数据采集是没有意义的.因此,节点的定位是无线传感器网络应用的重要基础[8].
WSN非测距定位技术研究大多数是基于二维平面的定位算法,仅有少数是三维自由空间的定位算法.二维平面的定位方法无法应用到山区地形上[9].如果把三维自由空间的定位方法直接应用到山区地形上,定位误差太大.张亚杰、段渭军、屈军锁、侯晓宁等人研究和改进了三维定位算法[9-10],这些定位算法是在三维自由空间场景下导出的.笔者对可应用于山区地形环境下的WSN节点的定位算法进行了初步研究[11-12].提出了山区复杂地形的无线传感器网络节点定位算法(NLA-MT, node localization algorithm of wireless sensor networks for complex terrain in mountain areas).基于距离矢量的多跳定位算法DV-HOP(DV-HOP, Distance vector multi-hop localization algorithm)是一种非测距定位算法,优点是节点体积小、成本低、能耗小、算法简单,稳健性好而极受欢迎;缺点是定位精度低[3].因此研究人员仍在努力改进DV-HOP算法,大多数人都是对平均每跳距离进行修正,使节点定位精度有一定改善,但定位精度仍较低.目前很少有人对山区地形上的节点定位进行研究. NLA-MT定位算法充分利用了山区地形环境的特点,用小范围局部平面拟合山区地形曲面,并将三维空间定位运算降为二维平面的定位运算来进行节点定位,有效提高了节点的定位精度.能够满足实际应用的要求,具有较高的实用价值.
1 无线传感器网络定位技术WSN定位技术分为基于测距的定位方法和非测距定位方法[8, 13].基于测距定位算法相对定位精度高,但节点成本也更高;而非测距定位算法节点成本更低,体积和能量消耗也更小,更适合于大规模无线传感器网络的应用.非测距定位算法中影响最大、应用最广泛的是DV-Hop定位算法[14].
1.1 三维DV-Hop定位算法无线传感器网络测区内的锚节点向所有节点发送自己的坐标位置和跳数等信息,未知节点可获得到各锚节点的最小跳数.通过计算可得测区内平均每跳距离,可以计算出未知节点到锚节点的近似距离,应用极大似然估计法计算出节点自身坐标[14].若已知未知节点到各锚节点的距离分别为d1,d2,…,dn(n≥4),未知节点的坐标为(x,y,z),各锚节点坐标分别为(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn).
可得矛盾方程组:
| $ \mathit{\boldsymbol{AX}} = \mathit{\boldsymbol{B}} $ | (1) |
其中
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {2\left( {{x_1} - {x_n}} \right)}&{2\left( {{y_1} - {y_n}} \right)}&{2\left( {{z_1} - {z_n}} \right)}\\ {2\left( {{x_2} - {x_n}} \right)}&{2\left( {{y_2} - {y_n}} \right)}&{2\left( {{z_2} - {z_n}} \right)}\\ {}& \vdots &{}\\ {2\left( {{x_{n - 1}} - {x_n}} \right)}&{2\left( {{y_{n - 1}} - {y_n}} \right)}&{2\left( {{z_{n - 1}} - {z_n}} \right)} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right] $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {x_1^2 - x_n^2 + y_1^2 - y_n^2 + z_1^2 - z_n^2 + d_n^2 - d_1^2}\\ {x_2^2 - x_n^2 + y_2^2 - y_n^2 + z_2^2 - z_n^2 + d_n^2 - d_2^2}\\ \vdots \\ {x_{n - 1}^2 - x_n^2 + y_{n - 1}^2 - y_n^2 + z_{n - 1}^2 - z_n^2 + d_n^2 - d_{n - 1}^2} \end{array}} \right] $ |
若矛盾方程组有解则可得
| $ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{B}} $ | (2) |
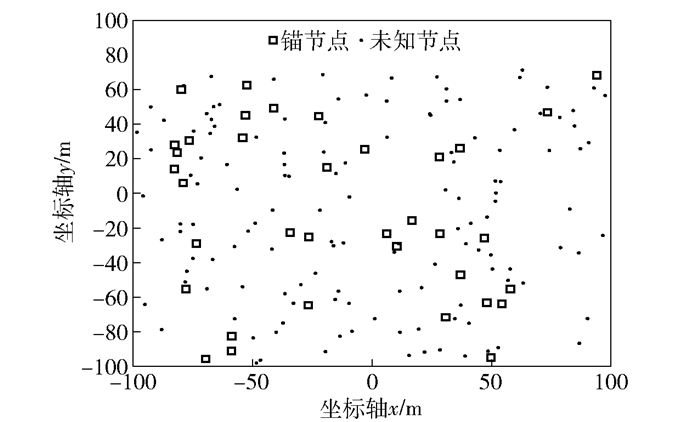
在山区地形上随机布放传感器节点,节点分布如图 1所示.以三维多峰曲面函数产生的多峰曲面来模拟山区地形,并制作该山区地形的三维电子网格数据和二维电子网格数据.三维多峰曲面函数为

|
图 1 传感器节点随机分布在山区地形上 |
| $ \begin{array}{*{20}{c}} {z = 3{{\left( {1 - x} \right)}^2}{{\rm{e}}^{ - {x^2} - {{\left( {y + 1} \right)}^2}}} - }\\ {10\left( {\frac{x}{5} - {x^3} - {y^5}} \right){{\rm{e}}^{ - {x^2} - {y^2}}} - \frac{1}{3}{{\rm{e}}^{ - {{\left( {x + 1} \right)}^2} - {y^2}}}} \end{array} $ |
采用DV-HOP定位算法的第1步:分别获取未知节点到锚节点的最小跳数.锚节点向所有节点发送自己的ID、坐标位置和跳数等信息,初始跳数设为0,每经过1个节点,跳数加1.经过一段时间后,所有节点可获得到各锚节点的最小跳数.
2.3 将传感器节点垂直投影到水平面上将山区地形上的传感器节点垂直投影到水平面上,如图 2所示.在二维平面上节点只有x,y坐标.
|
图 2 节点垂直投影到水平面上 |
应用改进的二维DV-HOP定位算法求未知节点的平面坐标.
1) 求锚节点的平均每跳距离
① 传统的DV-HOP定位算法求锚节点i的平均每跳距离vi.
| $ {v_i} = \frac{{\sum\limits_{i \ne j} {\sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2}} } }}{{\sum\limits_{i \ne j} {{h_{ij}}} }} $ | (3) |
其中:(xi,yi)为锚节点i的坐标,(xj,yj)为锚节点j的坐标,hij为锚节点i与锚节点j之间的跳数(i≠j).每个锚节点获得平均每跳距离后,向区域内所有其他节点广播.
② 修正锚节点的平均每跳距离.
a.计算锚节点之间的估计距离
| $ {s_{ij}} = {v_i}{h_{ij}} $ | (4) |
其中:vi为锚节点i的平均每跳距离,sij为通过近似计算获得的锚节点i与锚节点j的估计距离.
b.计算锚节点之间的实际距离
| $ {c_{ij}} = \sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2}} $ | (5) |
其中:cij为锚节点i与锚节点j的实际距离,(xi,yi)是锚节点i的坐标,(xj,yj)是锚节点j的坐标.
c.计算锚节点之间的跳距修正值
| $ {e_{ij}} = \frac{{\left( {{s_{ij}} - {c_{ij}}} \right)}}{{{h_{ij}}}} $ | (6) |
其中eij为锚节点i与j之间的跳距修正值.重复应用上述方法分别计算出锚节点i到其余所有锚节点的跳距修正值,最后求出锚节点i的跳距平均修正值ai.
| $ {a_i} = \frac{{\sum\limits_{j = 1,j \ne i}^n {{e_{ij}}} }}{{n - 1}} $ | (7) |
d.修正锚节点的平均每跳距离
| $ {r_i} = {v_i} + {a_i} $ | (8) |
其中ri为修正后的锚节点i的平均每跳距离.应用式(8)分别计算出所有锚节点修正后的平均每跳距离.
2) 计算未知节点到锚节点的距离
由式(9)计算未知节点到锚节点的距离.
| $ {d_{ij}} = {r_j}{h_{ij}} $ | (9) |
其中dij为未知节点i到锚节点j的距离.
3) 求未知节点的平面坐标
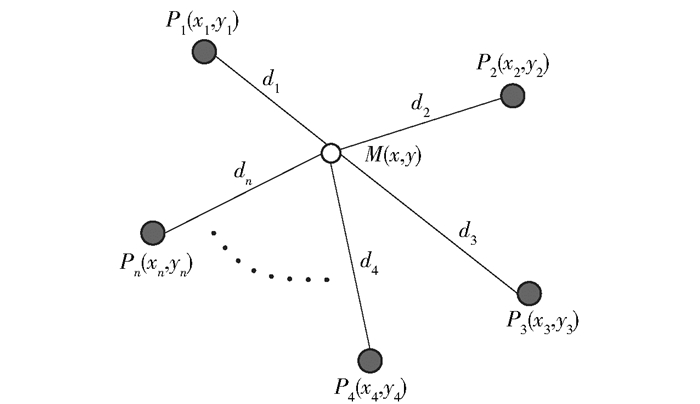
应用极大似然估计法依次求所有未知节点的坐标.如图 3所示,P1、P2、…、Pn为锚节点,n>3,M为未知节点,由未知节点到各锚节点的距离来构建矛盾方程组.应用最小二乘法解该矛盾方程组,即可获得未知节点M的坐标(x,y).
|
图 3 极大似然估计法 |
若求出了未知节点i的坐标(xi,yi),在该山区地形的二维电子网格数据中找出离未知节点i最近的且不在一条直线上的3个点,即找出这3个点的二维坐标(x,y).方法如下.
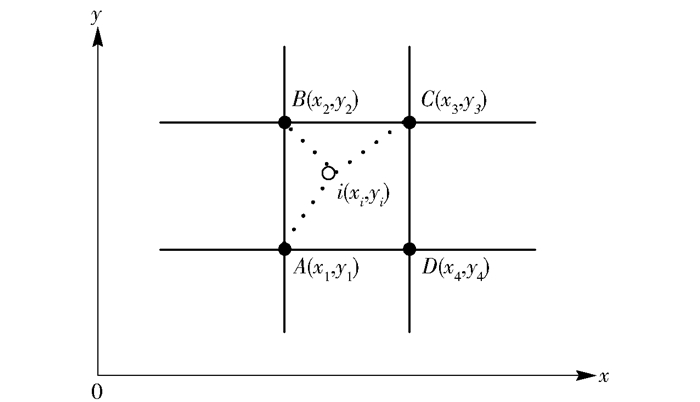
1) 首先在电子网格数据中搜索,确定未知节点i位于哪个网格中,如图 4所示.
|
图 4 求未知节点到网格中最近的3个顶点 |
2) 由式(10)分别计算未知节点i到网格中的4个顶点A、B、C、D的距离dij.
| $ {d_{ij}} = \sqrt {\left( {{x_i} - {x_j}} \right) + \left( {{y_i} - {y_j}} \right)} $ | (10) |
其中:j=A、B、C、D,即(xj,yj)分别表示未知节点i所在网格中的4个顶点A、B、C、D的坐标.
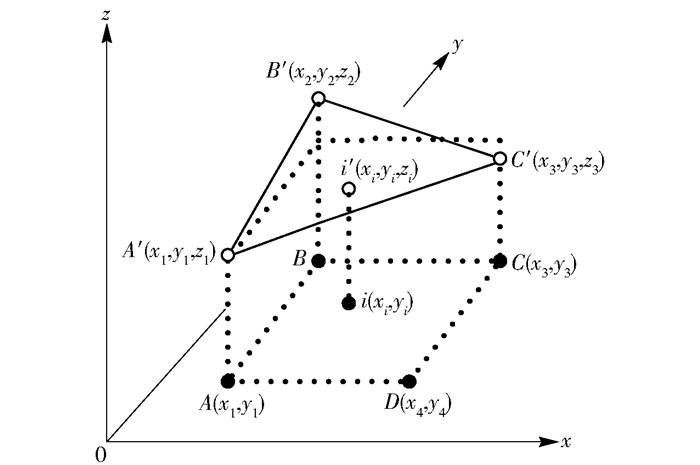
如图 5中未知节点i到网格中的A(x1,y1),B(x2,y2),C(x3,y3)三点更近,且这3点不在一条直线上.在对应的三维电子网格数据中,获得这3个点对应的三维坐标A′(x1,y1,z1),B′(x2,y2,z2),C′(x3,y3,z3),求出由这3点构成的平面,如图 5所示.
|
图 5 由3个顶点确定一个平面 |
已知三点A′(x1,y1,z1),B′(x2,y2,z2),C′(x3,y3,z3),求平面方程.
| $ ax + by + cz + d = 0 $ | (11) |
其中
| $ a = {y_1}{z_2} - {y_1}{z_3} - {y_2}{z_1} + {y_2}{z_3} + {y_3}{z_1} - {y_3}{z_2} $ |
| $ b = - {x_1}{z_2} + {x_1}{z_3} + {x_2}{z_1} - {x_2}{z_3} - {x_3}{z_1} + {x_3}{z_2} $ |
| $ c = {x_1}{y_2} - {x_1}{y_3} - {x_2}{y_1} + {x_2}{y_3} + {x_3}{y_1} - {x_3}{y_2} $ |
| $ \begin{array}{*{20}{c}} {d = - {x_1}{y_2}{z_3} + {x_1}{y_3}{z_2} + {x_2}{y_1}{z_3} - {x_2}{y_3}{z_1} - }\\ {{x_3}{y_1}{z_2} + {x_3}{y_2}{z_1}} \end{array} $ |
在图 5中,过未知节点i(xi,yi)作水平面的垂线, 该垂线与平面A′B′C′的交点为i′(xi,yi,zi). i′(xi,yi,zi)就是所求的未知节点i在山区地形表面的三维坐标.实际上只需将xi,yi代入平面方程(式(11)),即可求出zi,则得未知节点i′的坐标(xi,yi,zi).
| $ {z_i} = - \frac{1}{c}(ax + by + d) $ | (12) |
通过实验对比,山坡坡度在65°以下,NLA-MT定位算法效果较好,定位精度更高.坡度在65°以上,NLA-MT定位算法比灰狼优化的DV-Hop定位算法GWO-DV-Hop[3](GWO-DV-Hop, Grey-Wolf-based Optimization technique with DV-Hop algorithm)效果更差.原因是坡度很大时,节点投影到水平面的位置略有变化,z坐标将会变化很大,造成误差会较大.
3 性能评价若求出了某未知节点的近似坐标(xi,yi,zi),且已知该节点实际坐标为(ai,bi,ci),则两者的差距Δdi为
| $ \Delta {d_i} = \sqrt {{{\left( {{x_i} - {a_i}} \right)}^2} + {{\left( {{y_i} - {b_i}} \right)}^2} + {{\left( {{z_i} - {c_i}} \right)}^2}} $ |
则n个未知节点的平均定位误差Δ可表示为
| $ \Delta = \frac{1}{{nR}}\sum\limits_{i = 1}^n \Delta {d_i} $ | (13) |
其中R为节点的通信半径.
4 仿真实验在模拟山区地形环境的场景中,Kaur等[3]提出的GWO-DV-Hop定位算法、Xu等[15]提出的基于共面度的三维定位算法3D-IDCP(3D-IDCP, 3D localization algorithm based on Degree of Coplanarity)和山区复杂地形节点定位算法NLA-MT,在Matlab仿真平台上进行了模拟实验并对比分析了实验结果.每次实验中传感器节点都是随机均匀分布的.山区地形在水平面的投影范围是240 m×240 m,山头的最大高度是80.75 m.
1) 不同通信半径的仿真实验
传感器节点数为200,锚节点数占30%,未知节点数占70%,节点随机均匀分布.分别在R=30、40、50、60、70、80和90 m不同通信半径下进行了仿真实验.在每一个通信半径进行了100次的实验.传感器节点在每一次实验中都是随机均匀地分布.每次实验求出未知节点定位的相对均方差,取100次实验的相对均方差的平均值,就是该通信半径下的节点定位的相对均方差. 图 6显示了在不同通信半径下的GWO-DV-HOP定位算法[3]、3D-IDCP定位算法[15]和NLA-MT定位算法的平均定位误差曲线.从图可知,NLA-MT定位算法的误差最小,平均定位误差最优为28.6%,可以满足在山区复杂地形上的应用需求.通信半径在30 m时,以上3种算法的平均相对定位误差均较大.当通信半径增大时,平均相对定位误差迅速下降.在通信半径大于50 m后,平均相对定位误差较小且基本保持稳定.

|
图 6 不同通信半径的平均相对误差 |
2) 不同锚节点比例的仿真实验
通信半径R=80 m,节点总数200个,分别对锚节点占5%、10%、15%、20%、25%、30%、35%和40%时进行了仿真实验.对每一个不同锚节点比例都进行了100次的实验.传感器节点在每一次实验中都是随机均匀地分布.每次实验求出未知节点定位的相对均方差,取100次实验的相对均方差的平均值,就是该锚节点比例下节点定位的相对均方差. 图 7显示了在不同锚节点比例下GWO-DV-HOP定位算法[3]、3D-IDCP定位算法[15]和NLA-MT定位算法的平均定位误差曲线.从图可知,NLA-MT定位算法的误差最小,平均相对误差最优为28.0%,可以满足在山区复杂地形上的应用需求.锚节点比例在5%时,以上3种算法的平均相对定位误差均较大.在锚节点比例增大时,平均相对定位误差减小,当锚节点比例大于20%时,NLA-MT算法的平均相对定位误差较小且基本保持稳定.

|
图 7 不同锚节点比例的平均相对误差 |
3) 不同节点总数的仿真实验
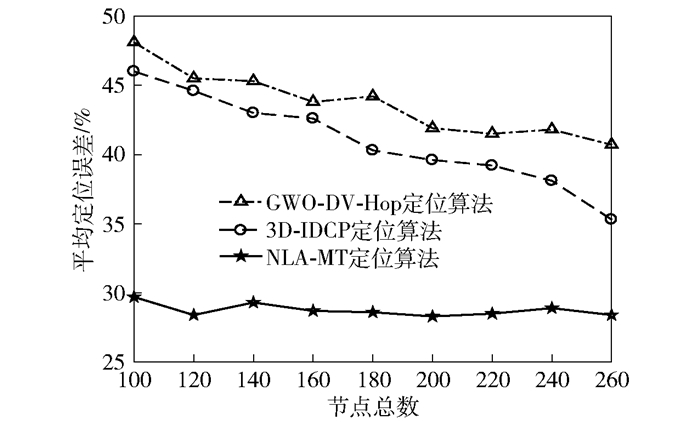
锚节点比例为25%,通信半径R=120 m,传感器节点分布均匀.分别在100、120、140、160、180、200、220、240和260不同的节点总数下进行了仿真实验.在每一不同的节点总数下进行了100次实验.传感器节点在每一次实验中都是随机均匀地分布.每次实验求出未知节点定位的相对均方差,取100次实验的相对均方差的平均值,就是该节点总数下的定位相对均方差. 图 8为不同节点总数下的GWO-DV-HOP定位算法[3]、3D-IDCP定位算法和NLA-MT定位算法的平均定位误差曲线.从图可知,NLA-MT定位算法的误差最小,平均相对误差最优为28.4%,可以满足在山区复杂地形上的应用需求.节点总数越多,平均相对定位误差越小.从图 8可知,NLA-MT定位算法的平均相对定位误差明显小于三维经典的DV-Hop算法和3D-IDCP定位算法,且受节点总数的影响较小.
|
图 8 不同节点总数时的平均相对误差 |
由于山区复杂地形的无线传感器网络节点定位算法NLA-MT有效利用了山区地形的特点.用局部平面拟合山区地形表面,并将三维空间降为二维平面来进行定位,大大降低了计算的复杂度,同时减少了节点能量的损耗.通过不同通信半径、不同锚节点比例、不同节点总数的多角度仿真实验,充分显示了所提出的NLA-MT定位算法在山区地形环境中的优异性,有效提高了无线传感器网络节点的定位算法精度,具有较高的实际应用价值.
| [1] |
Jiang Peng. A new method for node fault detection in wireless sensor networks[J]. Sensors, 2009, 9(2): 1282-1294. |
| [2] |
Chong C Y, Kumar S P. Sensor networks:evolution, opportunities, and challenges[J]. Proceedings of the IEEE, 2003, 91(8): 1247-1256. DOI:10.1109/JPROC.2003.814918 |
| [3] |
Kaur A, Kumar P, Gupta G P. Nature inspired algorithm-based improved variants of DV-Hop algorithm for randomly deployed 2D and 3D wireless sensor networks[J]. Wireless Personal Communications, 2018, 101(1): 567-582. DOI:10.1007/s11277-018-5704-7 |
| [4] |
Saeed N, Celik A, Al-Naffouri T, et al. Energy harvesting hybrid acoustic-optical underwater wireless sensor networks localization[J]. Sensors, 2018, 18(1): 51. |
| [5] |
Zhang L, Peng F, Cao P, et al. An improved three-dimensional DV-Hop localization algorithm optimized by adaptive cuckoo search algorithm[J]. International Journal of Online Engineering (iJOE), 2017, 13(2): 102-118. DOI:10.3991/ijoe.v13i02.6358 |
| [6] |
Hadir A, Zinc-Dine K, Bakhouya M, et al. An improved DV-Hop localization algorithm for wireless sensor networks [C]//Next Generation Networks and Services (NGNS), 2014 Fifth International Conference on IEEE. Casablanca, Morocco: [s.n.], 2014: 330-334.
|
| [7] |
Want R, Hopper A, Falcao V, et al. The active badge location system[J]. ACM Trans on Information Systems, 1992, 10(1): 91-102. |
| [8] |
Bang W, Wu G, Shu W, et al. Localization based on adaptive regulated neighborhood distance for wireless sensor networks with a general radio propagation model[J]. IEEE Sensors Journal, 2014, 14(11): 3754-3762. DOI:10.1109/JSEN.2014.2323553 |
| [9] |
张亚杰, 段渭军, 福豹, 等. 改进的距离重构三维定位算法[J]. 传感技术学报, 2014, 27(11): 1681-1686. Zhang Yajie, Duan Weijun, Wang Fubao, et al. An improved distance reconstructing three-dimensional localization algorithm[J]. Chinese Journal of Sensors and Actuators, 2014, 27(11): 1681-1686. |
| [10] |
屈军锁, 侯晓宁, 张继荣, 等. 四基站时差和牛顿迭代法的三维定位算法[J]. 西安邮电大学学报, 2015, 22(2): 36-40. Qu Junsuo, Hou Xiaoning, Zhang Jirong, et al. 3D localization algorithm based on 4-station time difference of arrival and Newton iteration[J]. Journal of Xi'an University of Posts and Telecommunications, 2015, 22(2): 36-40. |
| [11] |
胡中栋, 谢金伟. 基于近似投影效正的无线传感器网络三维定位机制[J]. 传感技术学报, 2014, 27(12): 1573-1577. Hu Zhongdong, Xie Jinwei. The 3D localization mechanism for wireless sensor networks based on approximate projection correction[J]. Chinese Journal of Sensors and Actuators, 2014, 27(12): 1573-1577. |
| [12] |
胡中栋, 肖华为. 适应山头地形的无线传感器网络节点定位算法[J]. 计算机工程与应用, 2016, 52(10): 104-107. Hu Zhongdong, Xiao Huawei. Node localization algorithm applied to hill-top topography for wireless sensor[J]. Computer Engineering and Applications, 2016, 52(10): 104-107. DOI:10.3778/j.issn.1002-8331.1406-0468 |
| [13] |
刘伟, 董恩清, 张德敬, 等. 一种判断无线网络节点定位翻转模糊的新方法[J]. 电子学报, 2015, 43(6): 1218-1223. Liu Wei, Dong Enqing, Zhang Dejing, et al. A new flip ambiguity detection algorithm in wireless networks node localization[J]. Acta Electronica Sinica, 2015, 43(6): 1218-1223. DOI:10.3969/j.issn.0372-2112.2015.06.027 |
| [14] |
Nicolescu D, Nath B. DV based positioning in Ad hoc networks[J]. Journal of Telecommunication Systems, 2003, 22(1/4): 267-280. DOI:10.1023/A:1023403323460 |
| [15] |
Xu Y, Zhuang Y, Gu J J. An improved 3D localization algorithm for the wireless sensor network[J]. International Journal of Distributed Sensor Networks, 2015, 1-9. |


