2. 北京空间飞行器总体设计部 空间智能机器人系统技术与应用北京市重点实验室, 北京 100094
针对火星车在火星行驶过程中存在的能量消耗过多等问题,提出了一种基于能量约束的路径规划算法.首先,考虑火星车克服重力做功以及驱动机构内部损耗等因素,推导出火星车的运动能量消耗函数,并求解其最小值,构建能量带权图;然后通过迪杰斯特拉算法,计算得到火星车能量带权图的能量消耗最小路径,并使用五次多项式插值拟合的方法实现火星车的行驶轨迹规划;最后,采用Adams软件建立火星典型地形和火星车动力学模型,采用Matlab/Simulink软件搭建火星车控制器模型,对火星车在典型地形中的行驶过程进行动力学与控制联合仿真实验,验证了所提路径规划算法的效果.结果表明,相对于传统的避障路径规划算法,所提算法使火星车能量消耗减少了15%以上,可有效提高火星车的能量利用效率.
2. Beijing Key Laboratory of Intelligent Space Robotic Systems Technology and Applications, Beijing Institute of Spacecraft System Engineering, Beijing 100094, China
Aiming at the excessive energy consumption of Mars rover on Mars, a path planning algorithm based on energy constraints is proposed. Firstly, considering overcoming gravity work and internal loss of driving mechanism, the motion energy consumption function of Mars rover is deduced, and its minimum value is solved. Therefore, the energy weighted map is constructed. Then, the energy consumption minimal path of the energy weighted graph is calculated by Dijkstra algorithm and using quintic polynomial interpolation to realize trajectory planning. Finally, Adams is used to establish the typical terrain of Mars and dynamics model of Mars rover, and Matlab/Simulink is used to build the controller model of Mars rover. The dynamics and control simulation of Mars rover in typical environment is used to verify the effectiveness of the path planning algorithm. The results show that compared with the traditional avoidance algorithm, the energy consumption of Mars rover is reduced by more than 15% using the proposed path planning algorithm, which can effectively improve the energy utilization efficiency of Mars rover.
火星车是承载各种仪器执行火星表面探测任务的重要载体和直接工具.火星地形十分复杂,存在如Tharsis Bulge高地、Valles Marineris大峡谷、火星奥尔库斯陨坑以及存在于峡谷和陨坑之间的山丘等复杂地貌,这对火星车的安全行驶带来了极大的挑战.此外,火星车还面临着通信延迟、带宽限制以及可持续工作能力等多方面的挑战[1].因此,基于安全与能量等因素,研究火星车自主规划对火星探测任务具有重要实际意义.
目前,对于地面行驶车辆的自主路径规划研究较多,主要有人工势场法[2]、改进A*算法[3]、结合深度学习的车辆路径规划[4]等方法.与火星非结构化地形不同,地面自主规划的车辆适用场景多为平缓公路等结构化地形,很少考虑爬坡、越障等工况.此外,在火星低重力条件下,火星车越障爬坡性能有所提升[5].因此,地面车辆的自主规划算法不能直接移植至火星车,需要针对火星表面低重力和非结构化环境开展火星车的路径规划研究.
目前有许多关于星球探测车路径规划的算法. Peng等[6]改进了粒子群算法中不易收敛的特性并引入变异因子增强其全局优化能力,对月球车进行全局路径规划,获得了一条无碰撞的路径. Dong等[7]提出了改进D*lite算法以获取平滑路径. Zhou等[8]针对月球车在坡面上的滑动进行分析,构建基于滑动地图的代价函数,并使用遗传算法求解得到一条最优路径.董元元等[9]针对传统A*算法进行改进,结合火星车局部避障算法建立了一种完整的路径规划方法. Raja等[10]将势场法与A*算法相结合,增强了算法的鲁棒性,更适用于一般环境.然而,对于星球车而言,仅考虑无碰撞的路径是不够的,由于星球车自身所携带的能量有限,星球车的路径规划应考虑能量约束.但目前针对能量约束的研究并不多. Speyerer等[11]考虑月球车能量约束,通过计算月球车总牵引力以及行进距离建立能量地图,使用A*算法进行路径规划寻求能量最少路径,忽略了车辆在坡面行进过程中侧倾角对于能量消耗的影响. Sakayori等[12]通过建立功率消耗模型,提出适用于坡面行进的能量效率路径规划,但其仅关注于局部路径规划,没有对当前任务空间进行全局路径规划. Sánchez等[13]针对不同的摩擦系数以及滑移率提出了两种运动模式,在不同情况下通过切换运动模式来减少能量消耗. Xie等[14]研究了月球车月面路径规划算法,将DEM图转化为行驶成本图,但仅仅考虑了地形的坡度与粗糙度,忽略了星球车在斜坡上可以以任意侧倾角前进. Sutoh等[15]提出了月球车运动路径规划,但是对于能量函数计算部分,选择最短路径为能量消耗最少,没有考虑地形的影响.
综上所述,当前对星球车路径规划的研究没有考虑到或是对能量约束考虑不够全面.笔者分析火星车运动过程中克服重力做功以及火星车驱动机构内部损耗,通过建立能量消耗函数,构建能量消耗地图,并结合迪杰斯特拉算法,计算得出一条消耗能量最少的路径,并使用五次多项式插值拟合方法实现路径.对火星车在典型地形中行驶过程进行动力学与控制联合仿真实验,以验证提出的路径规划算法的效果.
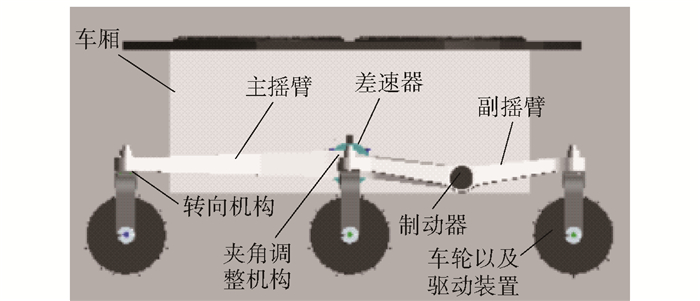
1 火星车运动学分析火星车结构如图 1所示,其包含车厢、差速器、主摇臂、夹角调整机构、副摇臂、制动器、转向机构、车轮以及驱动装置.其中,制动器和差速器是被动关节,其余关节为主动关节.通过关节之间的配合,火星车可通行一些崎岖地面.
|
图 1 主动悬架式火星车结构示意图 |
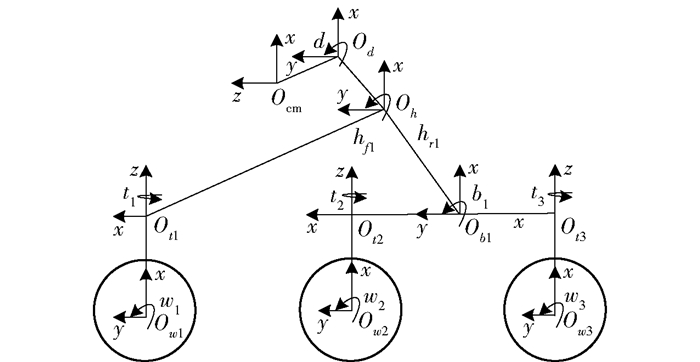
火星车各坐标系定义如图 2所示,Ocm为整车质心坐标系,初始位置与全局坐标系重合; Od为差速器坐标系; Oh为夹角调整机构坐标; Obi, i=1, 2为制动器坐标系; Oti为车轮转向关节坐标系,其中i=1~6;Owi为车轮驱动机构关节坐标系,其中i=1~6.
|
图 2 火星车-y侧坐标系 |
笔者使用混合坐标系法对火星车进行建模分析.关节i包括坐标系Oi以及坐标系
| $ {\mathit{\boldsymbol{C}}^{\tilde i,i}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\theta _i}} \right)}&{ - \sin \left( {{\theta _i}} \right)}&0\\ {\sin \left( {{\theta _i}} \right)}&{ - \cos \left( {{\theta _i}} \right)}&0\\ 0&0&1 \end{array}} \right] $ | (1) |
由此可见,坐标系Oi相对于坐标系Oi-1旋转矩阵以及位置矩阵可表示为
| $ {\mathit{\boldsymbol{C}}^{i - 1,i}} = {\mathit{\boldsymbol{C}}^{i - 1,\tilde i}}{\mathit{\boldsymbol{C}}^{\tilde i,i}} $ | (2) |
| $ {\mathit{\boldsymbol{P}}^{i - 1,i}} = {\mathit{\boldsymbol{P}}^{i - 1,\tilde i}} + {\mathit{\boldsymbol{P}}^{\tilde i,i}} $ | (3) |
定义Ti-1, i为火星车坐标系Oi相对于坐标系Oi-1的转移矩阵,则Ti-1, i表示为
| $ {\mathit{\boldsymbol{T}}^{i - 1,i}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}^{i - 1,i}}}&{{\mathit{\boldsymbol{P}}^{i - 1,i}}}\\ {\bf{0}}&1 \end{array}} \right] $ | (4) |
通过式(4),可以得到火星车各部件之间的位置旋转关系,以便后文对运动学进行分析.
针对火星表面复杂地形,火星车在行进过程中可能需要进行转弯等运动.为了完成任务要求,需要对火星车转弯进行分析,求解车轮转向机构转动角度以及车轮速度的匹配.定义车厢质心转弯向量为Rcm,定义车厢转弯半径为R,其中Rcm=[0 -R 0 0]T,则需要计算车厢质心在各车轮质心坐标系的转移矩阵Twi, cm,计算式为
| $ {\mathit{\boldsymbol{T}}^{{w_i},{\rm{cm}}}} = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{T}}^{{w_i},{t_i}}}{\mathit{\boldsymbol{T}}^{{t_i},h}}{\mathit{\boldsymbol{T}}^{h,d}}{\mathit{\boldsymbol{T}}^{d,{\rm{cm}}}},}&{i = 1,4}\\ {{\mathit{\boldsymbol{T}}^{{w_i},{t_i}}}{\mathit{\boldsymbol{T}}^{{t_i},b}}{\mathit{\boldsymbol{T}}^{b,h}}{\mathit{\boldsymbol{T}}^{h,d}}{\mathit{\boldsymbol{T}}^{d,{\rm{cm}}}},}&{i = 2,3,5,6} \end{array}} \right. $ | (5) |
通过式(6)计算得到每个车轮所对应的转弯向量Rwi,则火星车转向机构所需转动的角度由式(7)所求.
| $ {\mathit{\boldsymbol{R}}_{{w_i}}} = {\mathit{\boldsymbol{T}}^{{w_i},{\rm{cm}}}}{\mathit{\boldsymbol{R}}_{{\rm{cm}}}} $ | (6) |
| $ {t_i} = \arctan \left( {{\mathit{\boldsymbol{R}}_{{w_i}}}\left( {2,1} \right)/\left| {{\mathit{\boldsymbol{R}}_{{w_i}}}\left( {3,1} \right)} \right|} \right) $ | (7) |
针对转弯过程中速度匹配问题,火星车内侧车轮和外侧车轮转动速度之比与各自的转弯半径之比相同.
2 运动代价函数火星车可以通过一些缓坡、浅坑和障碍,因此,可以通过选择通行崎岖地区以换取较短的行进路程,从而减小能量消耗.
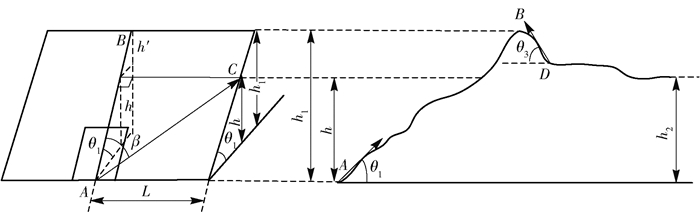
火星车可通行山丘如图 3所示,其中,A、B、C、D依次为火星车上坡点、山峰点、正坡面驶出点、火星车下坡点;θ1为正面山丘坡度角,θ3为下坡的坡度角,β为在正坡面行进过程中火星车的侧倾角,h1为山丘最高点距离地面高度,h2为山丘离开点距离地面高度,h′=h1-h;L为地面半径,可近似将曲线为直线. v为火星车行进速度. Ei为单位时间内各车轮控制器内部的摩擦损耗做功,其中i=1~6.
|
图 3 山坡示意图 |
火星车能量消耗主要包括:克服重力做功、关节内部摩擦引起的驱动机构内部损耗、行进过程中因“打滑”产生的滑动摩擦力做功以及克服空气阻力等能量的消耗,其中前两者占主要部分,所以只考虑前两者的能量损耗.
根据图 3所示,当火星车的侧倾角为0°时,h=h1,即为直接越过山顶爬坡,此时火星车所消耗的能量定义为
| $ \begin{array}{*{20}{c}} {E = mg{h_1} + \sum\limits_{i = 1}^6 {{E_i}} \frac{{{h_1}}}{{\sin \left( {{\theta _1}} \right)v}} + \sum\limits_{i = 1}^6 {{E_i}} \frac{{{h_1} - {h_2}}}{{\sin \left( {{\theta _3}} \right)v}} - }\\ {mg\left( {{h_1} - {h_2}} \right)} \end{array} $ | (8) |
其中m、g分别表示火星车整车质量和火星表面重力加速度.
当h=h2时,仅在山坡正面运动时需要克服重力和关节内部损耗做功,其余时间仅存在关节内部损耗做功,其消耗能量为
| $ \begin{array}{*{20}{c}} {E = mgh + \sum\limits_{i = 1}^6 {{E_i}} \frac{h}{{\sin \left( {{\theta _1}} \right)\cos \left( \beta \right)v}} + }\\ {3\sum\limits_{i = 1}^6 {{E_i}} \frac{{{h_1} - {h_2}}}{{{h_1}v}}L} \end{array} $ | (9) |
当h2 < h < h1时,火星车行进到山的右侧,重力做正功,重力势能转化为阻力做功,山坡后侧行进时仅有驱动机构内部能量损耗.因而,能量消耗公式为
| $ \begin{array}{*{20}{c}} {E = mgh + \sum\limits_{i = 1}^6 {{E_i}} \frac{h}{{\sin \left( {{\theta _1}} \right)\cos \left( \beta \right)v}} + }\\ {\sum\limits_{i = 1}^6 {{E_i}} \frac{{h - {h_2}}}{{\sin \left( {{\theta _2}} \right)\cos \left( {\beta '} \right)v}} - mg\left( {h - {h_2}} \right) + }\\ {\sum\limits_{i = 1}^6 {{E_i}} \frac{{{h_1} - {h_2}}}{{{h_1}v}}L} \end{array} $ | (10) |
其中:θ2、β′分别表示右侧坡度角、右侧坡面火星车行驶侧倾角.
当行进高度满足h < h2时,火星车在右侧斜面运动,需要克服重力做功以及关节内部摩擦损耗,山坡后侧行进时仅有驱动机构内部能量损耗.能量消耗公式为
| $ \begin{array}{*{20}{c}} {E = mgh + \sum\limits_{i = 1}^6 {{E_i}} \frac{h}{{\sin \left( {{\theta _1}} \right)\cos \left( \beta \right)v}} + }\\ {\sum\limits_{i = 1}^6 {{E_i}} \frac{{{h_2} - h}}{{\sin \left( {{\theta _2}} \right)\cos \left( {\beta '} \right)v}} - mg\left( {h - {h_2}} \right) + }\\ {\sum\limits_{i = 1}^6 {{E_i}} \frac{{{h_1} - {h_2}}}{{{h_1}v}}L} \end{array} $ | (11) |
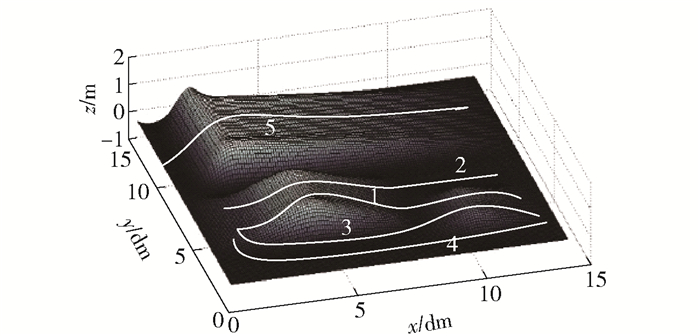
火星表面遍布山丘、峡谷,综合考虑火星车稳定性以及爬坡性能等通行能力,建立如图 4所示的火星地形地貌简图,地形参数如表 1所示.
|
图 4 火星地形简图 |
|
|
表 1 地形参数 |
基于图 4所示的火星地貌,具有5种行进方式,其中路线3、路线4需要进行速度规划.使用五次多项式插值法对轨迹进行规划,五次多项式插值法函数为
| $ q\left( t \right) = {a_0} + {a_1}t + {a_2}{t^2} + {a_3}{t^3} + {a_4}{t^4} + {a_5}{t^5} $ | (12) |
其中:a1、a2、a3、a4、a5为五次多项式插值法函数系数,t为运动时间.
五次多项式插值法函数需要6个约束条件为
| $ \left. {\begin{array}{*{20}{l}} {q\left( 0 \right) = {q_0};q\left( {{t_f}} \right) = {q_f};\dot q\left( 0 \right) = {{\dot q}_0};}\\ {\dot q\left( {{t_f}} \right) = {{\dot q}_f};\ddot q\left( 0 \right) = {{\ddot q}_0};\ddot q\left( {{t_f}} \right) = {{\ddot q}_f}} \end{array}} \right\} $ | (13) |
其中,tf为到达终止点的时间,q0、
| $ \dot q\left( t \right) = {a_1} + 2{a_2}t + 3{a_3}{t^2} + 4{a_4}{t^3} + 5{a_5}{t^4} $ | (14) |
对式(12)求二阶导数可得到加速度函数
| $ \ddot q(t) = 2{a_2} + 6{a_3}t + 12{a_4}{t^2} + 20{a_5}{t^3} $ | (15) |
联立式(12)~(15)可得
| $ \left. {\begin{array}{*{20}{l}} {{a_0} = {q_0}}\\ {{a_1} = {{\dot q}_0}}\\ {{a_2} = {{\ddot q}_0}}\\ {{a_3} = \frac{1}{{2t_f^3}}\left[ {20{q_f} - 20{q_0} - \left( {8{{\dot q}_f} + 12{{\dot q}_0}} \right){t_f} - \left( {3{{\ddot q}_0} - {{\ddot a}_f}} \right)t_f^2} \right]}\\ {{a_4} = \frac{1}{{2t_f^4}}\left[ {30{q_0} - 30{q_f} + \left( {14{{\dot q}_f} + 16{{\dot q}_0}} \right){t_f} + \left( {3{{\ddot q}_0} - 2{{\ddot a}_f}} \right)t_f^2} \right]}\\ {{a_5} = \frac{1}{{2t_f^5}}\left[ {12{q_f} - 12{q_0} - \left( {6{{\dot q}_f} + 6{{\dot q}_0}} \right){t_f} - \left( {{{\ddot q}_0} - {{\ddot a}_f}} \right)t_f^2} \right]} \end{array}} \right\} $ | (16) |
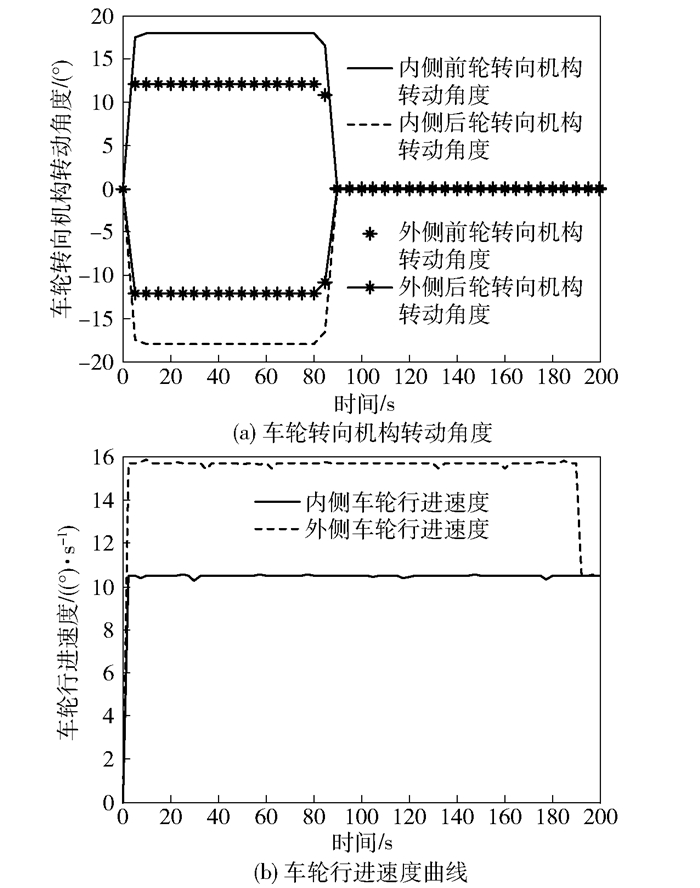
以路线3为例,求解火星车机构的规划角度.首先,使用五次多项式插值法对路径进行拟合,得到火星车质心行进轨迹以及行进速度.之后,根据火星车质心行进速度以及车轮转向机构计算公式(式(7)),分别计算得到行进过程中各车轮转向机构转动角度.行进过程中,内侧前轮、后轮最大转向角度分别为17.9°,-17.9°,内侧中轮转向机构保持不变.外侧前轮、后轮最大转向角度分别为12.1°,-12.1°,外侧中轮转向机构保持不变.根据行进过程中火星车内侧车轮和外侧车轮转动速度之比与各自的转弯半径之比相同一原则,计算得内侧车轮行进速度为10.5(°)/s、外侧车轮最大行进速度为15.7(°)/s.前200 s车轮运动规划如图 5所示,随后车轮转向机构以及车轮驱动机构保持此速度继续行进.
|
图 5 车轮运动规划曲线 |
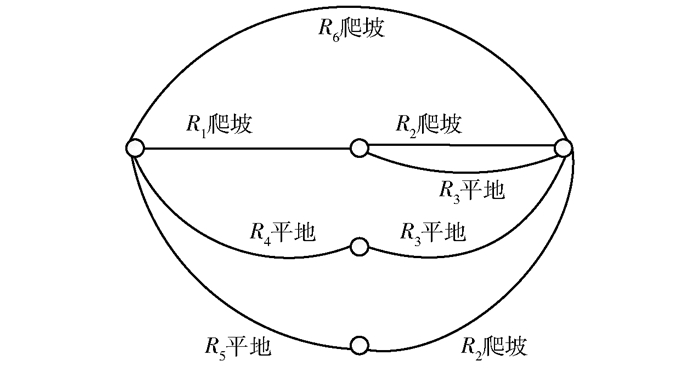
根据所推导的火星车运动能量消耗函数可以计算得出运动所消耗的能量,根据计算得出的能量消耗可以绘制如图 6所示的能量消耗带权图.
|
图 6 能量消耗带权图 |
根据速度规划状况,并由式(8)~式(11)计算可得,图 6中R1~R6路径消耗能量分别为4 780 J,3 335 J,3 125 J,6 103 J,5 579 J,∞.其中∞代表的含义为此段路径无法通行.通过使用迪杰斯特拉算法,可以得到最小能量消耗路径为先爬坡之后进行平地运动.
3.2 仿真验证使用Matlab/Simulink建立的火星车控制器模型与ADAMS火星车动力学模型进行联合仿真以对算法进行验证.火星车动力学仿真可视化界面如图 7所示.

|
图 7 火星车动力学仿真可视化界面 |
对规划的各条火星车行驶路径进行仿真分析,控制器模型中电机功率的积分表示火星车行进过程中的能量消耗值.车轮行进速度、车轮转向机构转向角度依据规划数据设置.仿真模型的详细参数设置如表 2所示.
|
|
表 2 仿真参数 |
通过仿真,得到各条线路能量消耗,如表 3所示.可以看出, 选择传统避障R4R3则需要消耗10 350 J的能量,而先爬坡后走平地R1R3线路仅需消耗8 769 J的能量,使用本文提出的路径规划算法,完成相同的任务可以减少能量消耗达15%以上.
|
|
表 3 线路能量消耗 |
针对火星表面地形以及火星车自身能量约束,提出了一种基于火星车能量消耗约束的路径规划算法.通过确立能量消耗函数构建能量消耗带权图,并通过迪杰斯特拉算法求得最小消耗能量路径,并使用五次多项式方法拟合实现路径.经过仿真分析表明:相对于传统的避障路径规划算法,使用本文提出的路径规划算法,火星车能量消耗减少了15%以上,可以有效提高火星车的能量利用效率.
| [1] |
魏祥泉, 黄建明, 顾冬晴, 等. 火星车自主导航与路径规划技术研究[J]. 深空探测学报, 2016, 3(3): 275-281. Wei Xiangquan, Huang Jianming, Gu Dongqing, et al. Researches on the techniques of autonomous navigationand path planning for mars rover[J]. Journal of Deep Space Exploration, 2016, 3(3): 275-281. |
| [2] |
唐志荣, 冀杰, 吴明阳, 等. 基于改进人工势场法的车辆路径规划与跟踪[J]. 西南大学学报(自然科学版), 2018, 40(6): 174-182. Tang Zhirong, Ji Jie, Wu Mingyang, et al. Vehicle path planning and tracking based on and improved artificial potential field method[J]. Journal of Southwest University (Natural Science Edition), 2018, 40(6): 174-182. |
| [3] |
Han Y M, Jeong J B, Kim J H. Quadtree based path planning for unmanned ground vehicle in unknown environments[C]//International Conference on Control, Automation and Systems. Washington, DC: IEEE Computer Society, 2012: 992-997.
|
| [4] |
You Changxi, Lu Jianbo, Filev D, et al. Advanced planning for autonomous vehicles using reinforcement learning and deep inverse reinforcement learning[J]. Robotics and Autonomous Systems, 2019(114): 1-18. |
| [5] |
高海波, 范雪兵, 邓宗全, 等. 可折展载人月球车移动性能仿真与试验分析[J]. 载人航天, 2016, 22(3): 323-327. Gao Haibo, Fan Xuebing, Deng Zongquan, et al. Simulation and experiments analysis of mobility performance in deployable manned lunar vehicle[J]. Manned Spaceflight, 2016, 22(3): 323-327. DOI:10.3969/j.issn.1674-5825.2016.03.009 |
| [6] |
Peng Song, Jia Yang. Global path planning for lunar rover based on particle swarm optimization algorithm[C]//2011 IEEE 5th International Conference on Robotics, Automation and Mechatronics (RAM). Washington, DC: IEEE Computer Society, 2011: 83-88.
|
| [7] |
Dong Shaoyang, Ju Hehua, Xu Hongxia. An improvement of D* lite algorithm for planetary rover mission planning[C]//2011 IEEE International Conference on Mechatronics and Automation. Washington, DC: IEEE Computer Society, 2011: 1810-1815.
|
| [8] |
Zhou Lanfeng, Yang Lina, Tang hanwei. Research on path planning algorithm and its application based on terrain slope for slipping prediction in complex terrain environment[C]//2017 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC).[S.l.]: Institute of Electrical and Electronics Engineers Inc, 2017: 224-227.
|
| [9] |
董元元, 崔祜涛, 田阳. 基于栅格地图的火星车路径规划方法[J]. 深空探测学报, 2014, 1(4): 289-293. Dong Yuanyuan, Cui Hutao, Tian Yang. A path-planning method for Mars rovers based on grid map[J]. Journal of Deep Space Exploration, 2014, 1(4): 289-293. |
| [10] |
Raja R, Dutta A. Path planning in dynamic environment for a rover using A* and potential field method[C]//International Conference on Advanced Robotics.[S.l.]: Institute of Electrical and Electronics Engineers Inc, 2017: 578-582.
|
| [11] |
Speyerer E J, Lawrence S J, Stopar J D, et al. Optimized traverse planning for future polar prospectors based on lunar topography[J]. Icarus, 2016, 273: 337-345. DOI:10.1016/j.icarus.2016.03.011 |
| [12] |
Sakayori G, Ishigami G. Energy efficient slope traversability planning for mobile robot in loose soil[C]//2017 IEEE International Conference on Mechatronics (ICM).[S.l.]: Institute of Electrical and Electronics Engineers Inc, 2017: 99-104.
|
| [13] |
Pérez-del-Pulgar C J, Sánchez J R, Azkarate M, et al. Path planning for reconfigurable rovers in planetary exploration[C]//IEEE International Conference on Advanced Intelligent Mechatronics.[S.l.]: Institute of Electrical and Electronics Engineers Inc, 2017: 1453-1458. http://ieeexplore.ieee.org/document/8014223/
|
| [14] |
Xie Yuan, Zhou Jianliang, Wang Yong. Dynamic mission-level path planning for lunar rovers[C]//International Conference on Control Automation and Systems. Washington, D C: IEEE Computer Society, 2010: 56-61.
|
| [15] |
Sutoh M, Otsuki M, Wakabayashi S, et al. The right path:comprehensive path planning for lunar exploration rovers[J]. IEEE Robotics & Automation Magazine, 2015, 22(1): 22-33. |



