针对建筑信息模型(BIM)模型版权保护的问题,基于BIM的数据特征提出了一种BIM模型的零水印算法.首先,将不同数据中约束性不强的点图元排除,获得其他点图元的位置信息,计算单体模型的特征点到各个点图元的基准点之间的距离作为水印构造的载体;其次,将特征值进行排序,求出相邻点之间的变化率,将不符合要求的特征值排除;最后,根据特征值的特征对特征值分区,利用各分区中特征值的奇偶性构造一种用于BIM模型版权保护的零水印算法.实验结果证明,所提算法安全性高,可对常规攻击平移、旋转和模型详细程度的变化有较强的鲁棒性,能够满足实用性的需求,对BIM模型的版权保护有重要价值.
Aiming at the building information modeling (BIM) model copyright problem, basing on the BIM data characteristics, designs a zero watermarking algorithm for BIM data, which will not change data precision. Because different modeling has its own primitives and constraint relation, the proposed algorithm must be taking full account of the difference. Firstly, the lowly constraints of the primitive points are removing and the other primitive location points are obtaining. The distance between each point benchmark and the feature point is the carrier for watermarking by choosing the feature point of the monomer precise modeling. Secondly, the algorithm bubbles sort the eigenvalues and obtains the change rate of consecutive eigenvalues, then removing the high change rate eigenvalues. Finally, dividing the eigenvalues and construct a series of zero watermarking sequence. The results of experiment showed that the algorithm had strong robustness to usual attacking such as translation, rotation and slightly deleting point.
三维地理信息系统(3D GIS)的发展使得三维地理空间数据在数据获取和使用阶段受到极大的重视.其中,高精度的建筑信息模型(BIM, building information modeling)成为3D GIS系统中的一个重要来源[1]. BIM是一种将数字化的三维建筑模型作为核心,应用于建筑工程的设计、施工等过程中的工作方法[2]. 3D GIS和BIM的结合应用过程中,将宏观地理要素中需要数字化分析和管理的模型用BIM模型替代,BIM模型在使用过程中可能会产生泄密、非法盗用等问题,不仅有损自身、企业、国家的利益,对国家安全和利益也会造成不可估量的损失.
目前,BIM模型的安全保护方式主要包括制定安全协议、委托专业代理人和专业公司及增加用户自定义块等.数字水印技术可将模型的版权信息融合到BIM模型中,成为不可分离的一部分,使用这种方式可以在数据使用的各个阶段实现对BIM模型的版权认证、泄密追踪和事后追究,更加灵活和可靠地为BIM模型提供版权保护.
BIM模型数字水印算法研究成果鲜有见刊,但在图像、矢量数据零水印技术及传统的三维点云模型和网格模型的鲁棒水印方面研究成果丰富[3-6].采用传统鲁棒水印方法和脆弱水印方法在嵌入水印后会使得BIM模型的尺寸、位置、方向和形状发生改变,加上模型构建的自动更新机制,造成模型的变化较大.零水印利用数字产品自身特征来构造水印,可以很好地解决数字水印的可感知性和鲁棒性之间的矛盾[7], 使用BIM模型的零水印技术能达到对BIM模型安全保护的目的.
在三维网格模型和点云模型方面零水印研究较多[8-10],对BIM模型的零水印构造具有借鉴意义.三维模型零水印算法主要分为频率域和空间域2种水印算法.徐涛等[8]在三维网格模型中应用三维DCT变换,由较大的系数构造生成零水印,该算法对平移、旋转、缩放和顶点重新排序等攻击鲁棒性较好,对网格简化的鲁棒性较弱.在空间域中,孙媛媛等[9]设计的算法对网格简化攻击鲁棒性较强,但是对噪声的鲁棒性较弱.王新宇和詹永照[10]采用顶点到中心点的距离构造零水印信息,对仿射变换、噪声、简化、量化、平滑和细分等都有强鲁棒性,但对中心点依赖程度高.目前,三维模型数字水印算法研究重点主要为鲁棒水印算法,需要抵抗网格简化和细分等特殊攻击.
以上算法虽然可以很好地保护三维网格模型的版权,但依然存在以下2个问题.
1) 为了抵抗网格方面的攻击而设计的针对网格点的特征,以及针对三维网格点数量多且冗余度较高的特征,无法对数据一致且低冗余的BIM模型适用.
2) BIM模型对象是精细的单体建筑物模型,图元基准点之间突出的集中性和约束性特点使得三维模型中常用的全局特征量(如曲率等)不能直接使用.
提出了一种针对BIM模型的零水印算法,其基准点少,冗余度低,解决了现有三维模型水印算法无法直接使用的问题.首先,BIM模型中图元的空间位置信息采用基准点坐标信息进行表达,相邻图元之间可设置严格的拓扑关系和约束条件.选择BIM模型特征点到各个图元的基准点之间的距离值作为水印信息的载体,可有效抵抗BIM模型详细程度变化对模型图元实体信息的改变;其次,设计了一种基于较少基准点的BIM模型的分区方法,能有效抵抗BIM模型平移和旋转攻击.实验表明,本文算法对常见的平移、旋转和详细程度变化攻击具有较强的鲁棒性,在BIM模型传输和共享过程中能有效保护模型的版权信息.
1 BIM模型特点分析通过对BIM模型的分析可知,其具有独特的特征,具体表现如下:
1) 具有更高的数据精度.在存储数据中可以达到10-13,在模型显示中一般显示为毫米级别;
2) 数据冗余度低.相比较拥有万级数量级的点云模型和网格模型而言,BIM模型显示的是冗余度较小的三维微观模型,最小可达到几百个模型点;
3) BIM模型是实体模型,内部更加精细,各数据点具有分层性、严格的拓扑关系和约束关系,而三维网格模型中常用的特征,如形状曲率直径、曲率、相邻点之间的角度等变化趋于0或者突变,不利于特征的构造.
由此可见,BIM模型的高精度、低冗余、实体特点使得其数字水印算法的研究更加侧重于零水印和无损水印算法,且主要需要抵抗几何攻击,不需要考虑网格简化和细分等攻击.
着重考虑平移、旋转和模型精细程度的攻击,而BIM模型中不涉及影响数据变化的缩放功能,在设计零水印算法时也不考虑缩放攻击.
2 BIM模型零水印算法 2.1 算法思想为了不影响数据精度,考虑到BIM模型的实体性和低冗余性,需要设计一种能够利用模型实体图元、基准点少的零水印算法,以抵抗在数据传输和共享过程中平移、旋转和图元精细程度变化等几何攻击.在旋转的过程中,由于图元之间存在强约束关系,模型可能会发生轻微基准点删除、增加和更新.
针对数据共享过程中存在平移、旋转和实体图元精细程度变化等几何攻击,对BIM模型零水印算法进行研究.首先,生成安全性更高的、具有一定长度的伪随机序列水印信息,选择模型基准点作为水印信息载体来抵抗模型详细程度变化攻击;然后,提出一种基于水印信息长度的距离分区方法,适用低冗余度和基准点少的BIM模型,可以有效抵抗平移和旋转攻击;最后,依据奇偶量化机制完成零水印构造,并将构造的零水印信息和原始模型提交到第三方机构,在水印检测阶段,通过提取的零水印信息和待检测的水印信息进行异或操作获取版权信息.
基于低冗余度、高精度和实体性的数据特征提出一种适用于BIM模型的零水印算法,解决了现有三维模型水印算法无法直接应用的问题,可以有效抵抗BIM模型在数据传输过程中的平移、旋转和图元精细程度变化等几何攻击.
2.2 水印信息生成采用无意义水印信息,具体方法为:使用某一密钥K作为随机数种子,基于伪随机数发生器,生成长度为l的二值水印信息W,w(t)表示在位置t的水印信息.
| $ W=\{w(t) | w(t) \in\{0, 1\}, t=0, \cdots, l-1\} $ |
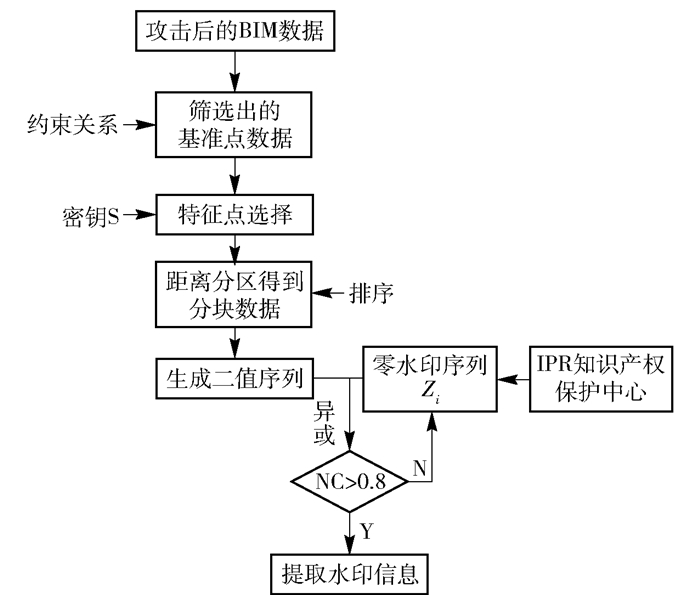
在零水印算法设计中,通过主体模型图元的基准点作为水印信息构造载体.零水印算法与水印提取算法的检验流程分别如图 1和图 2所示.本文主要是在选择特征点之后,对距离进行分区,对不同区域进行水印信息构造,与版权信息进行异或操作得到零水印序列,提交到第三方机构.具体流程如图 1所示.

|
图 1 零水印构造过程 |
|
图 2 水印检测流程 |
在构造零水印时,数据分区可以增加水印信息容量,一定程度上抵抗旋转攻击.采用原始数据基准点的坐标信息提取特征信息,分区主要是为使数据均匀分布在各个区域中.将各个模型图元基准点坐标到特征点坐标的距离值作为特征值,排除环境、植物、图框、喷头、常规模型等约束性不强的图元时,需要适用类别不同的BIM模型,对距离值排序后计算其变化率,作为分区的基础.根据变化率去除掉特征值中突变的点,选取特征值的最大值和最小值对模型进行分区,并判断分区内的点是否满足水印容量的要求,如果不满足则选取特征的中点值重新成为最大值或最小值继续分区,直到分区中的点均满足水印长度要求.
2.3.2 基于特征点的零水印构造考虑到BIM模型中全局特征值较为稳定,因此选择各个模型图元到特征点之间距离值作为水印构造载体来设计BIM模型零水印算法.具体步骤如下:
1) 选取各个模型图元基准点的坐标信息vi(vix, viy, viz).其中,(1≤i≤n), n为基准点的数量,由提供的密钥获取模型特征点vm(vmx, vmy, vmz).由式(1)计算各个模型图元基准点到特征点之间的距离值ρi (1≤i≤n):
| $ \rho_{i}=\sqrt{\left(v_{i x}-v_{m x}\right)^{2}+\left(v_{i y}-v_{m y}\right)^{2}+\left(v_{i z}-v_{m z}\right)^{2}} $ | (1) |
2) 排序、排除突变点影响.对ρi从小到大进行排序,得到排序后的特征值,并用式(2)计算突变程度Sj(j表示第j个基准点的变化率).若变化程度大于指定阈值,且距离最大值较为接近,则在数据分区中排除此突变点及突变点之后的点.
| $ S_{j}=\left(\rho_{j+1}-\rho_{j}\right) / \rho_{j} $ | (2) |
3) 数据分区.得到排序后ρj的最小值ρmin和排除突变点之后的最大值ρmax,用式(3)取得中间值ρmid,依据中间值将数据分为两个区域(A1和A2),判断各个区域特征点的数量是否大于水印容量的2倍,如果是则允许第二次分区,如果满足条件则依据新的中间值继续进行分区,直到不能分区为止.得到分区A={A1, A2, …, AN},N表示所得的分区个数.
| $ \rho_{\operatorname{mid}}=\left(\rho_{\max }+\rho_{\min }\right) / 2 $ | (3) |
4) 异或操作.取得第k个分区Ak中的所有特征值,根据特征值中整数部分的奇偶性得到二值序列Pk,依据式(4)将Pk与Wk进行异或操作,得到N个零水印.由各个分块生成的零水印的二值序列为Zk.将原始BIM模型和生成的零水印二值序列保存至只是产权保护保护中心IPR,并加入具有法律效力的时间戳,抵御解释攻击.
| $ Z_{k}=P_{k} \oplus W_{k} $ | (4) |
水印的检测过程是零水印构造的逆过程.水印检测流程如图 2所示.
1) 待检测模型.依据零水印生成阶段相同的方法,对BIM模型提取全局特征信息ρj,对ρj进行排序分区,得到各个分区Ak,并得到各个分区中的二值序列Pk.
2) 异或操作.从IPR获得零水印产生的二值序列Zk,依据水印嵌入过程的式(4)对Pk和Zk异或操作,重新生成水印序列W′k.
3) 对比验证.将提取出来的多个零水印版权信息W′k与原始水印序列W进行验证,利用式(5)归一化相关系数NC值(normalized correlation)衡量相似性.
| $ \mathrm{NC}=\frac{1}{H} \sum\limits_{i=1}^{H} b_{k} $ | (5) |
其中:bk=XNOR(W, W′k),W为原始水印信息,W′k为提取出的多个水印信息,H为水印信息大小.
4) 获得最大的相关系数.当原始矢量数据未被修改,各个水印图像的NC值为1,若某一水印图像的NC值大于设定的阈值,则可认为待检测数据与原始数据属于同一版权,否则不能判断待检测数据版权归属.
3 实验分析为了评估本文方案在不同BIM类型数据中的普适性和差异性,选取建筑模型、结构模型和机电模型作为实验数据. 图 3所示商务办公楼属于建筑模型,图 4所示为商务办公楼(Test1)的细节,建筑模型中图元类型主要包含栏杆、门、窗和幕墙坚挺等;图 5所示IDC_结构(Test2)和图 6所示天津桃园区(Test3)属于结构模型,图元类型主要为结构柱和结构框架等;图 7所示ZXYY_MEP模型(Test4)和图 8所示MZL_X_1F_MWP模型(Test5)属于机电模型,图元类型主要为电气设备、线管配件和软风管.按上述步骤与原始数据构建零水印,在此基础上进行实验与分析.

|
图 3 商务办公楼 |

|
图 4 商务办公楼细节图 |

|
图 5 IDC_结构 |

|
图 6 天津桃园区 |

|
图 7 ZXYY_MEP模型 |

|
图 8 MZL_X_1F_MWP模型 |
零水印必须具有唯一性才具有使用价值,本文的检测方式是以Test5模型构造的6组零水印作为参考与其他4个模型检测时构造的水印信息进行异或操作得到版权信息,判断与原始版权信息的相关性,如果相关性大于0.8则判断版权信息检测成功,否则即为失败.实验结果如表 1所示.
|
|
表 1 零水印唯一性验证结果 |
由实验结果可知, 除Test5模型可以正确检测到水印信息, 其他模型的NC值均小于0.7, 笔者提出的BIM模型零水印算法有唯一性.
3.2 鲁棒性实验及结果分析 3.2.1 原始检测结果将随机生成的二值序列作为水印信息.实验中利用NC值与还原水印个数进行算法的鲁棒性实验, NC值越大、还原水印个数越多,模型的抗攻击越好.原始检测结果如表 2所示.
|
|
表 2 原始检测结果 |
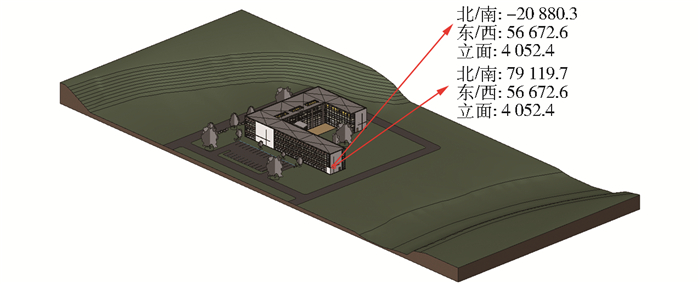
在平移过程中, BIM模型的坐标信息发生变化, 给模型造成大的改变, 如图 9所示.因此, 针对模型抗平移的鲁棒性进行实验.实验结果如表 3所示.
|
图 9 模型平移前后 |
|
|
表 3 平移攻击实验结果 |
由表 3可见, 原始数据在X/Y/Z方向上分别平移100 m, 还原的水印个数较多且存在NC为1的水印.因此, 本文算法对平移攻击有强的鲁棒性.
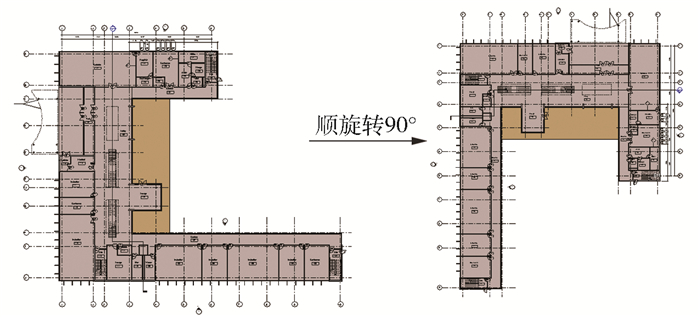
3.2.3 旋转在BIM模型的传输过程中,旋转是使用较多的操作之一,由于约束条件和拓扑关系的影响,在BIM模型发生较大旋转情况下(见图 10),一些模型可能会发生数据删除、更新和添加.以RVT模型为例,表 4所示为旋转攻击实验结果,“-”表示逆时针.
|
图 10 模型旋转前后 |
|
|
表 4 旋转攻击实验结果 |
由表 4可知,Test1~Test5模型在旋转180°时仍然存在NC值为1的水印.由此可见,笔者设计的算法可以有效抵抗旋转攻击.
3.2.4 详细程度BIM模型中各个图元包含点、线、面等实体信息,选择图元基准点之间的距离作为水印构造的载体,模型的详细程度变化不会影响水印提取. 表 5展示了模型详细程度变化攻击的鲁棒性,包含粗略、中等和详细3种程度.
|
|
表 5 详细程度实验结果 |
由表 5可知,当详细程度由粗略到详细或由详细到粗略变化时,仍可以正确提取水印信息.因此,本文算法不受模型图元详细程度变化的影响.
4 结束语针对BIM模型的版权保护问题,提出了一种适用于BIM模型的零水印算法.相较于其他三维模型,阐述了已有的三维模型的零水印算法及存在问题,并结合BIM模型的数据特征设计相应零水印算法.在设计方案中, 对构造零水印的唯一性和鲁棒性进行实验, 实验结果可以看出,构造出的零水印算法具有唯一性,且对常见的平移、旋转和详细程度变化等攻击具有强的鲁棒性,可以有效保护BIM模型的版权信息,对BIM模型的版权保护具有一定价值.
| [1] |
Zhao Xia, Tang Shengjun, Liu Mingwei, et al. Semantics constrained conversion approach of RVT model to CityGML model[J]. Geomatics World, 2015, 22(2): 15-20. |
| [2] |
朱亮, 邓非. 基于语义映射的BIM与3D GIS集成方法研究[J]. 测绘地理信息, 2016, 41(3): 16-19. Zhu Liang, Deng Fei. Integration method of BIM and 3DGIS based on semantic mapping[J]. Journal of Geomatics, 2016, 41(3): 16-19. |
| [3] |
Kutter M, Bhattacharjee S K, Ebrahimi T. Towards second generation watermarking schemes[C]//International Conference on Image Processing, 1999. New York: IEEE Press, 1999: 320-323.
|
| [4] |
Rani A, Bhullar A K, Dangwal D, et al. A zero watermarking scheme using discrete wavelet transform[J]. Procedia Computer Science, 2015(70): 603-609. |
| [5] |
Rao Y R, Nagabhooshanam E. A novel image zero-watermarking scheme based on DWT-BN-SVD[C]//International Conference on Information Communication and Embedded Systems. New York: IEEE Press, 2015: 1-6.
|
| [6] |
Thanh T M, Tanaka K. An image zero-watermarking algorithm based on the encryption of visual map feature with watermark information[J]. Multimedia Tools and Applications, 2017, 76(11): 13455-13471. DOI:10.1007/s11042-016-3750-2 |
| [7] |
温泉, 孙锬锋, 王树勋. 零水印的概念与应用[J]. 电子学报, 2003, 31(2): 214-216. Wen Quan, Sun Tanfeng, Wang Shuxun. Concept and application of zero watermark[J]. Acta Electronica Sinica, 2003, 31(2): 214-216. DOI:10.3321/j.issn:0372-2112.2003.02.015 |
| [8] |
徐涛, 张艳宁, 孙瑾秋, 等. 基于几何特征的3维网格模型零水印算法[J]. 中国图象图形学报, 2009, 14(9): 1819-1824. Xu Tao, Zhang Yanning, Sun Jinqiu, et al. Zero watermarking scheme for 3D meshes based on geometric property[J]. Journal of Image and Graphics, 2009, 14(9): 1819-1824. |
| [9] |
孙媛媛, 胡敏. 一种三维网格模型零水印算法[J]. 微电子学与计算机, 2010, 27(3): 170-172. Sun Yuanyuan, Hu Min. A zero watermark algorithm for three dimensional meshes[J]. Microelectronics & Computer, 2010, 27(3): 170-172. |
| [10] |
王新宇, 詹永照. 面向三维点云模型的鲁棒零水印技术[J]. 计算机工程与应用, 2011, 47(28): 7-11. Wang Xinyu, Zhan Yongzhao. Robust zero watermarking scheme for 3D point model[J]. Computer Engineering and Applications, 2011, 47(28): 7-11. DOI:10.3778/j.issn.1002-8331.2011.28.002 |



