2. 南京邮电大学 物联网学院, 南京 210003
针对在几何处理领域有着广泛应用的三角形网格参数化问题,研究了基于重心映射的三角形网格参数化方法.利用geometry-processing-js类库中的半边数据结构,采用均匀拉普拉斯权重、拉普拉斯-贝尔特拉米权重和中值权重3种加权方案,实现了重心映射法,并根据三角形的形变量分析了参数化结果.结果表明,中值权重为重心映射法的最优加权方案.
2. School of Internet of Things, Nanjing University of Posts and Telecommunications, Nanjing 210003, China
The parameterization of triangle meshes has numerous applications in the field of geometry processing. Using the halfedge-based data structure provided by geometry-processing-js, this paper researches on the mesh parameterization and its implementation based on barycentric mapping, as well as three weight sets applied in barycentric mapping, namely, the uniform Laplacian weights, the Laplace-Beltrami weights, and the mean value weights. A comparison between the results of parameterization is given based on the distortion caused to the triangles, and a conclusion is given that the mean value weights provide the best weighting scheme for barycentric mapping.
三角形网格由一组通过公共边或公共角相连的三角形构成.由于三角形本身具有的简单几何特性,在几何处理领域,三角形网格是一种十分高效而且常用的对三维物体的二维流型表面进行离散化表达的方式.参数化通常指平面参数化.对于任意用三角形网格表示的物体表面,存在一个从网格上的点Pi到二维平面上点Pi*的一一映射,使得二维平面上的网格与原网格的拓扑同构,这样的一一映射被称为三角形网格的参数化[1].三角形网格映射到的二维平面则被称为参数域.
三角形网格参数化在几何处理和计算机图形学中有着广泛的应用.通过参数化,可以找到二维图像和三维物体表面之间的对应点,从而实现纹理贴图[2-3].类似地,三维物体表面的其他细节信息,例如法线信息,也可以通过参数化映射到二维平面上,从而更好地实现光照对物体表面的渲染[4].此外,参数化能够保存三维物体表面细节的性质还可以应用于细节转换[5-6]、网格编辑[7]、曲面变形[8]等.
目前,实现将三角形网格映射到二维平面上的参数化方法有许多种,比较常用的有:重心映射法(barycentric mapping)或称塔特嵌入法(Tutte embedding)[9]、基于角度的拍平化法(ABF, angle based flattening)[10]及其改进方法ABF++[11]、基于最小二乘的保角映射法(LSCM, least squares conformal maps)[12]、最等距参数化法(MIPS, most isometric parameterization of surfaces)[13]及其改进方法(AMIPS, advanced most isometric parameterization of surfaces)[14]、有界失真映射法(BDM, bounded distortion mapping)[15]、局部内射映射法(LIM, locally injective mapping)[16]、边界优先拍平化法(BFF, boundary first flattening)[17]等.基于geometry-processing-js几何处理类库[18]中三角形网格的半边数据结构(halfedge-based data structure)[19-21],实现了重心映射参数化方法,并采用了3种加权方案:均匀拉普拉斯权重(uniform Laplacian weights)[22]、拉普拉斯-贝尔特拉米权重(Laplace-Beltrami weights)[23]和中值权重(mean value weights)[24],分析了3种加权方案对参数化结果产生的影响.
1 三角形网格的半边数据结构三角形网格是由一系列离散且无序的三角形组成的.一个设计良好的三角形网格数据结构不仅可以实现对网格的快速构建,还能够对网格中点、边、面等信息进行高效地遍历与查找,并减少存储和处理网格需要的内存消耗和冗余.基于半边的数据结构就是一种优秀的构建和存储三角形网格的方式.
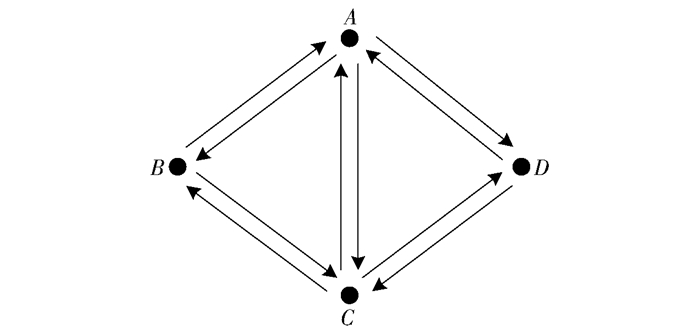
半边指将三角形的一条边分解为一对拥有相反方向的有向边.在基于半边的数据结构中,网格的每个面和每条边界由半边逆时针环绕而成.如图 1所示,半边〈A, B〉、〈B, C〉和〈C, A〉构成面ABC;半边〈A, C〉、〈C, D〉和〈D, A〉构成面ACD;半边〈B, A〉、〈A, D〉、〈D, C〉和〈C, B〉构成了网格边界(这样的半边称为边界半边,这些半边间的顶点称为边界顶点).网格边界也可以因此看作由多条半边逆时针环绕而成的虚拟面.此外,三角形中的每一条半边也能定义其唯一的对应角(即两个相邻面中的非共享角). 图 1中,∠ABC为半边〈C, A〉的对应角,∠ADC为半边〈A, C〉的对应角.同理,三角形中的每一个角也能找到其对应半边.
|
图 1 由半边表示的三角形网格 |
在三角形网格的半边数据结构中,每一条半边中存储的信息如下:
1) 半边的出射顶点,如图 1中,顶点C为半边〈C, A〉的出射顶点;
2) 半边的对应角(边界半边则没有对应角),如图 1中,∠ABC为半边〈C, A〉的对应角;
3) 半边的所在面(边界半边的所在面为表示边界的虚拟面),如图 1中,面ABC为半边〈C, A〉的所在面;
4) 半边所在面或所在边界中的前驱半边,如图 1中,〈B, C〉为〈C, A〉的前驱半边,〈B, A〉为〈A, D〉的前驱半边;
5) 半边所在面或所在边界中的后继半边,如图 1中,〈A, B〉为〈C, A〉的后继半边,〈D, C〉为〈A, D〉的后继半边;
6) 半边的反向半边,如图 1中,〈A, C〉为〈C, A〉的反向半边.
这样,可以将网格的几何信息存入三角形的顶点、角和面中,将网格的拓扑信息存入半边中,从而构建出三角形网格的半边数据结构,如表 1所示.
|
|
表 1 基于半边的数据结构 |
由表 1可知,三角形网格的每一个顶点只与其出射半边中的一条相关联,每一个角与其对应半边关联,每一个面只与该面中的一条半边关联,而每一条半边中则存储了大量连接信息,包括出射顶点、对应角和所在面的引用以及其前驱、后继和反向半边的引用.
在geometry-processing-js几何处理类库中,网格的顶点、角、面和半边均以顺序表的形式存储,对这些信息的引用则通过索引的方式实现.
初始化三角形网格半边数据结构的过程可以概括如下步骤:
步骤 1 读取全部的顶点实现对顶点对象的构造,并存入一个顶点表中;
步骤 2 对构成三角形面的顶点组按照逆时针的环绕顺序每3个一组批量读取,实现对面和内部半边(非边界半边,构造时将边界标记boundary置为“假”)的构造;
步骤 3 遍历所有步骤2中创建的内部半边,将没有反向半边的内部半边找出,构造它们的反向半边,并标记为边界半边(构造时将边界标记boundary置为“真”),构造表示边界的虚拟面;
步骤 4 遍历步骤2、步骤3中创建的半边,为内部半边构造对应角,并将对应角和其对应半边相互关联.
在每3个一组批量读取顶点、构造面和内部半边时,先将所有顶点的状态标为“未读”,每次读取完成后将本次读取顶点的状态标为“已读”.对于一组顶点的读取,需要执行的步骤如下:
步骤 1 构造一个新的面对象,并将其引用存入面表中;
步骤 2 按照读取顶点的顺序,对每个顶点构造出射半边对象,并将边界标记boundary置为“假”,将出射顶点的引用存入其中,将其前驱和后继的引用存入其中,将步骤1中构造的面的引用存入其中,将该半边的引用存入出射顶点和半边表中.
步骤 3 默认使用步骤2中构造的最后一条半边作为步骤1中创建的面的关联半边,将其引用存入步骤1中创建的面中.
步骤 4 检查本组顶点的状态,若存在2个顶点状态同时为“已读”,这意味着它们之间存在之前读取顶点组时创建的半边,此时遍历半边表,找到它们之间先前创建的半边,将其与步骤2中创建的两点之间的新半边相互关联为反向半边.
步骤 5 将本组读取顶点的状态置为“已读”.
通过上述步骤,可以确保顶点表中的每个顶点与其一条出射半边相关联.
这样,基于表 1给出的半边数据结构,从网格中任意一个顶点出发,都可以在无需条件判断的情况下,实现对其单环邻域(one-ring neighborhood)内所有元素的遍历.算法1描述了对顶点的所有出射半边的逆时针遍历.
算法 1 遍历出射半边
Input: center //起始顶点
Output: outgoings //出射半边集合
function OutgoingHalfedges(center)
1 h←center.halfedge
2 hstop←h
3 outgoings ← {h}
4 do
5 h ← h.twin.next
6 outgoings ← outgoings ∪ {h}
7 while h≠hstop
8 return outgoings
对于三角形网格中的任意一个顶点,算法1从与其关联的半边出发,依次访问反向半边的后继半边,直到返回出发的半边为止,即可实现对顶点所有出射半边的遍历.
同理,对于顶点的单环邻域内的其他元素,如邻接顶点和邻接三角形,也可以写出类似算法1的遍历器实现对其的遍历.
2 重心映射重心映射法是目前使用最为广泛的三角形网格参数化方法之一.该方法基于图论中的塔特重心映射定理(Tutte’s barycentric mapping theorem)[9],描述如下.
设一个三角形网格与圆盘同胚,若一个二维域能满足下列2个条件:
1) 使得网格边界上顶点的坐标(u, v)分布在一个凸多边形上;
2) 使网格每个内部顶点(即非边界顶点)的坐标为其邻接顶点坐标的凸组合(convex combination).
则这样的二维域是一个有效参数域,这样的(u, v)坐标构成一个无自交的有效参数化.
现假设一个三角形网格M中有n个顶点,分别为{V1, V2,…, Vn},它们在参数域上的坐标记为{(u1, v1), (u2, v2), …, (un, vn)},这些顶点按照一定顺序排列,其中内部顶点的索引为{1, 2, …, nint},边界顶点的索引为{nint+1, nint+2, …, n}.根据凸组合的定义,塔特重心映射定理中的条件2)可以写为
| $ \sum\limits_{j \ne i} {{a_{ij}}} \left( {\begin{array}{*{20}{l}} {{u_j}}\\ {{v_j}} \end{array}} \right) - {a_{ii}}\left( {\begin{array}{*{20}{l}} {{u_i}}\\ {{v_i}} \end{array}} \right) = 0 $ | (1) |
其中:i为M中任意一个内部顶点Vi的索引,即i∈{1, 2, …, nint},j为M中除Vi外任意一个内部顶点的索引,即j∈{1, 2, …, nint}且j≠i,系数aij和aii则由式(2)给出.
| $ \left. \begin{array}{l} {a_{ij}} > 0,\;\;\;若\;{V_i}\;和\;{V_j}\;是邻接顶点\\ {a_{ij}} = 0,\;\;\;若\;{V_i}\;和\;{V_j}\;不是邻接顶点\\ {a_{ii}} = - \sum\limits_{j \ne i} {{a_{ij}}} \end{array} \right\} $ | (2) |
而对于M边界上的顶点,只需将其在参数域上的坐标固定在一个凸多边形上即可.假设参数域上有一个预先定义好的凸多边形,其顶点坐标为{(unint+1, vnint+1), (unint+2, vnint+2), …, (un, vn)},则塔特重心映射定理中的条件1)可以写为
| $ {a_{ii}}\left( {\begin{array}{*{20}{c}} {{u_i}}\\ {{v_i}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\bar u}_i}}\\ {{{\bar v}_i}} \end{array}} \right) $ | (3) |
其中:i为M中任意一个边界顶点Vi的索引,即i∈{nint+1, nint+2, …, n},系数aii=1.
根据式(1)和式(3),可构建如下的线性方程组,从而同时满足塔特重心映射定理中的条件:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{Au}} = \mathit{\boldsymbol{\bar u}}\\ \mathit{\boldsymbol{Av}} = \mathit{\boldsymbol{\bar v}} \end{array} \right\} $ | (4) |
其中:A为以系数aij为元素的n阶稀疏矩阵,A=(aij)n×n,其中i, j∈{1, 2, …, n}.由式(2)和式(3)可知,A中各元素的取值描述如下.
非对角线元素,即aij,且j≠i,如式(5)所示.
| $ \left. \begin{array}{l} {a_{ij}} > 0,\;\;\;{V_i}\;是内部顶点,且\;{V_i}\;与\;{V_j}\;邻接\\ {a_{ij}} = 0,\;\;\;其他情况 \end{array} \right\} $ | (5) |
对角线元素,即aii,如式(6)所示.
| $ \left. \begin{array}{l} {a_{ii}} = - \sum\limits_{j \ne i} {{a_{ij}}} ,\;\;\;{V_i}\;是内部顶点\\ {a_{ii}} = 1,\;\;\;\;\;{V_i}\;是边界顶点 \end{array} \right\} $ | (6) |
式(4)中,u和v为2个等长的n元向量,用来存放M边界上的顶点在参数域凸多边形上的对应坐标,u=(u1, u2,…, un),v=(v1, v2, …, vn),它们的分量分别记为ui和vi,其中i∈{1, 2, …, n}.当i≤nint时,ui和vi均取0;当i>nint时,(ui, vi)为参数域上凸多边形的对应坐标.
式(4)中,u和v为2个等长的n元向量,用来存放M中顶点参数化后的对应坐标,u=(u1, u2,…, un),v=(v1, v2, …, vn),它们的分量分别记为ui和vi,其中i∈{1, 2, …, n}. (ui, vi)即为M中的顶点Vi参数化后的坐标.
这样,只需求解式(4)给出的线性方程组,分别求出向量u和v,即可得到M的参数化结果.
2.1 均匀拉普拉斯权重M中由内部顶点组成的网格可以被视作一个无向权重图G,其顶点集为V,边集为E,即G=(V, E),且V={V1, V2, …, Vnint}.式(4)中矩阵A中描述内部顶点的子矩阵,即可视作G的拉普拉斯矩阵,记为A′,A′=(aij)nint×nint,其中i, j∈{1, 2, …, nint}. A′中非零的非对角线元素aij(其中j≠i且(Vi, Vj)∈E,下同)可以视作M中两邻接点Vi和Vj之间边(Vi, Vj)的权重.因此,可以通过选择对边集E不同的加权方案,构造出不同的矩阵A′,从而对M实现不同的参数化结果.
均匀拉普拉斯权重方案,即指对G中的边集E进行平均地加权,通常将权重取值为1即可.这样,A′中的非零非对角线元素aij和对角线元素aii的取值为
| $ \left. {\begin{array}{*{20}{l}} {{a_{ij}} = 1}\\ {{a_{ii}} = - {D_i}} \end{array}} \right\} $ | (7) |
其中:Di为顶点Vi的度数,即Vi邻接顶点的个数.
均匀拉普拉斯权重简单易实现,经典的重心映射法就是基于此实现的.然而对边集E的均匀加权却造成了对三角形网格几何属性的忽视,例如边长、三角形内角度数等,从而造成参数化结果的失真.因此,接下来将介绍2种其他的加权方案,以减少此类失真.
2.2 拉普拉斯-贝尔特拉米权重拉普拉斯算子(Laplace operator)是一个多元函数的二阶微分算子,其定义为梯度的散度,可以用来衡量函数正则性(即函数的平滑程度),其值越小,函数越平滑.拉普拉斯-贝尔特拉米算子(Laplace-Beltrami operator)则是拉普拉斯算子在流形表面上的推广形式.
因此,可以利用拉普拉斯-贝尔特拉米算子对边集E进行加权,从而得到较为平滑的参数坐标,来减少参数化结果的失真.基于拉普拉斯-贝尔特拉米算子的离散化表达式[23],对A′的非零非对角线元素aij和对角线元素aii取值如下:
| $ \left. \begin{array}{l} {a_{ij}} = \frac{1}{{2{S_i}}}\left( {\cot {\alpha _{ij}} + \cot {\beta _{ij}}} \right)\\ {a_{ii}} = - \sum\limits_j {{a_{ij}}} \end{array} \right\} $ | (8) |
其中:αij和βij的位置如图 2所示,Si为顶点Vi维诺域(Voronoi region)的面积,指的是Vi与其邻接点连线的垂直平分线所围成区域的面积,即图 2中虚线围成的区域.

|
图 2 计算拉普拉斯-贝尔特拉米权重所需的角和面积 |
式(8)中维诺域Si的面积计算如下[23]:
| $ {S_i} = \frac{1}{8}\sum\limits_j {\left( {\cot {\alpha _{ij}} + \cot {\beta _{ij}}} \right){l_{ij}}} $ | (9) |
其中lij为边(Vi, Vj)的长度.
为简化计算难度,可以分别对Vi的每个邻接三角形计算其维诺域面积. Vi的一个邻接三角形△ViVjVk中的维诺域S′i如图 3所示.

|
图 3 单个邻接三角形内的维诺域 |
在式(9)的基础上,易得S′i的面积计算式为
| $ {{S'}_i} = \frac{1}{8}\left( {l_{ij}^2\cot \alpha + l_{ik}^2\cot \beta } \right) $ | (10) |
其中:α和β的位置如图 3中所示,分别为半边〈Vi, Vj〉和〈Vk, Vi〉的对应角,
lij为边(Vi, Vj)的长度,lik为边(Vi, Vk)的长度.
这样,基于表 1给出的半边数据结构和算法1中实现的对顶点出射半边进行逆时针遍历的遍历器OutgoingHalfedges( ),可以实现对任意顶点的维诺域面积的计算,如算法2所示.
算法 2 计算维诺域面积
Input: center //起始顶点
Output: area //维诺域面积
function VoronoiArea(center)
1 area ← 0
2 foreach h in OutgoingHalfedges(center) do
3 l1 ← Length(h.prev)
4 l2 ← Length(h)
5 cotA ← Cotan(h.prev.corner)
6 cotB ← Cotan(h.corner)
7 area ← area+(l1l1cotA+l2l2cotB)/8
8 return area
算法2中,Length( )为计算半边长度的函数,Cotan( )为计算角的余切值的函数,在表 1的半边数据结构基础上,这些函数的算法都容易实现.对于顶点的每一条出射半边,求出它和它前驱半边的长度以及它和它前驱半边对应角的余切值,代入式(10),即可求出该半边所在三角形(顶点的一个邻接面)内的维诺域面积.这样,依次遍历顶点的每一条出射半边,求出该顶点所有邻接面内的维诺域面积,再对每个三角面的维诺域面积进行累加,即可求得顶点的维诺域面积.
利用三角形网格的半边数据结构,式(8)中的αij和βij十分易得,其中αij是半边〈Vi, Vj〉的对应角,βij是〈Vi, Vj〉的反向半边〈Vj, Vi〉的对应角.将上述两角以及根据算法2计算出的维诺域面积代入式(8),即可计算出A′中各元素的值.
2.3 中值权重在三角形网格中出现钝角的情况下,基于式(8)计算出的权重会出现负值,这会产生反转三角形,导致参数化的结果发生错误.当然,对网格进行再分即可消除其中的钝角[25],从而避免负权重的出现.此外,基于拉格朗日中值定理(Lagrange’s mean value theorem),Floater[24]提出了一种加权方案,确保权重一直为正,该方案称为中值权重.
中值权重方案对A′的非零非对角线元素aij和对角线元素aii取值如下:
| $ \left. \begin{array}{l} {a_{ij}} = \frac{1}{{{l_{ij}}}}\left( {\tan \frac{{{\delta _{ij}}}}{2} + \tan \frac{{{\gamma _{ij}}}}{2}} \right)\\ {a_{ii}} = - \sum\limits_j {{a_{ij}}} \end{array} \right\} $ | (11) |
其中:lij为边(Vi, Vj)的长度,δij和γij为位于边(Vi, Vj)两侧Vi的邻接角,如图 4所示.

|
图 4 计算中值权重所需的角 |
在具体实现中,利用三角形网格的半边数据结构,δij和γij十分易得. δij是半边〈Vi, Vj〉后继半边的对应角,γij是半边〈Vj, Vi〉前驱半边的对应角.计算出δij和γij的角度后,将其代入式(11),即可实现对A′中各元素的赋值.
3 参数化结果分析与比较在Google Chrome(版本号:68.0.3440.106)的运行环境下,基于geometry-processing-js几何处理类库,运用JavaScript编程语言,实现了使用均匀拉普拉斯权重、拉普拉斯-贝尔特拉米权重和中值权重的重心映射参数化方法,并选用4种物体的三角形网格进行实验,分别为环形山、甲壳虫汽车、奶牛和人脸.
3.1 可视化分析参数化的可视化结果如表 2所示,分别给出了物体的原三角形网格以及使用均匀拉普拉斯权重、拉普拉斯-贝尔特拉米权重和中值权重进行参数化的结果.观察表 2可以发现,相较于均匀拉普拉斯权重,使用拉普拉斯-贝尔特拉米权重和中值权重的参数化能更好地维持原网格上三角形的形状.例如,对比环形山和奶牛的参数化结果可知,均匀拉普拉斯权重使得原网格上参差不齐的三角形经参数化后形状大小更趋于一致,更接近等边三角形.均匀拉普拉斯权重的这一特性也使得网格内部的空洞在参数化后变得更小,如表 2中甲壳虫汽车的参数化结果.此外,使用拉普拉斯-贝尔特拉米权重和中值权重的参数化结果更好地反映出了原网格上的一些特征.如表 2中,拉普拉斯-贝尔特拉米权重和中值权重使得人脸上的眼睛、鼻子与嘴巴的形状被完好地保存在了参数化结果中.
|
|
表 2 参数化结果比较 |
基于从参数域上的三角形到原网格上对应三角形的仿射变换[26],参数化对三角形造成的形变可由该仿射变换雅可比矩阵(Jacobian matrix)的奇异值进行衡量[27].形变量的计算过程描述如下.
设参数域上的一个三角形为△p1p2p3,其中pi=(ui, vi)(i∈{1, 2, 3},下同),三角形△q1q2q3为其在原网格上的对应三角形.令
| $ f\left( \mathit{\boldsymbol{p}} \right) = \frac{{{S_{\Delta p{p_2}{p_3}}}{\mathit{\boldsymbol{q}}_1} + {S_{\Delta p{p_3}{p_1}}}{\mathit{\boldsymbol{q}}_2} + {S_{\Delta p{p_1}{p_2}}}{\mathit{\boldsymbol{q}}_3}}}{{{S_{\Delta {p_1}{p_2}{p_3}}}}} $ | (12) |
f在u和v两个方向上的偏导数为
| $ \left. \begin{array}{l} \frac{{\partial f}}{{\partial u}} = \frac{{\left( {{v_2} - {v_3}} \right){\mathit{\boldsymbol{q}}_1} + \left( {{v_3} - {v_1}} \right){\mathit{\boldsymbol{q}}_2} + \left( {{v_1} - {v_2}} \right){\mathit{\boldsymbol{q}}_3}}}{{2{S_{\Delta {p_1}{p_2}{p_3}}}}}\\ \frac{{\partial f}}{{\partial v}} = \frac{{\left( {{u_3} - {u_2}} \right){\mathit{\boldsymbol{q}}_1} + \left( {{u_1} - {u_3}} \right){\mathit{\boldsymbol{q}}_2} + \left( {{u_2} - {u_1}} \right){\mathit{\boldsymbol{q}}_3}}}{{2{S_{\Delta {p_1}{p_2}{p_3}}}}} \end{array} \right\} $ | (13) |
f的3×2雅可比矩阵
| $ \left. {\begin{array}{*{20}{l}} {{\sigma _{\max }} = \sqrt {\frac{1}{2}\left( {\left( {a + c} \right) + \sqrt {{{\left( {a - c} \right)}^2} + 4{b^2}} } \right)} }\\ {{\sigma _{\min }} = \sqrt {\frac{1}{2}\left( {\left( {a + c} \right) - \sqrt {{{\left( {a - c} \right)}^2} + 4{b^2}} } \right)} } \end{array}} \right\} $ | (14) |
其中:
σmax和σmin分别表示仿射变换f对于平面上单位长度产生的最大和最小缩放倍数.对于三角形的几何形变,拉伸和收缩的测定标准需要保持一致.因此,对三角形的形变量d定义为[27]
| $ d = \max \left( {{\sigma _{\max }},\frac{1}{{{\sigma _{\min }}}}} \right) $ | (15) |
这样就确保了d≥1,当且仅当f为全等变换时等号成立.
对于三角形网格的参数化,可以计算出参数域上每一个三角形与原网格上对应三角形之间的形变量,从而得到参数化对网格上所有三角形造成的平均形变量dmean、最大形变量dmax(形变的最坏情况)以及形变量的标准差dstd(形变的波动情况).具体计算结果如表 3所示.
|
|
表 3 参数化对三角形网格造成的形变量比较 |
表 3的结果表明,以均匀拉普拉斯权重作为比较基准,拉普拉斯-贝尔特拉米权重和中值权重均能减少参数化对三角形产生的平均形变,从而减少参数化的失真.拉普拉斯-贝尔特拉米权重虽然能够整体上使参数化保真,但产生的最大形变高.与之相比,中值权重更好地控制了形变的最坏情况和形变的波动情况.
4 结束语研究了基于重心映射的三角形网格参数化的理论来源和实现方法,描述了实现重心映射法所采用的三角形网格半边数据结构,分析并比较了实现重心映射法所采用的3种加权方案:均匀拉普拉斯权重、拉普拉斯-贝尔特拉米权重和中值权重,给出了使用这3种权重的重心映射参数化在一些具体物体的三角形网格上的实验结果,并计算了参数化对网格上三角形产生的形变量.通过对比发现,拉普拉斯-贝尔特拉米权重和中值权重能产生较低的三角形平均形变量,从而更好地保持原三角形网格的形状与特征,减少参数化失真.而中值权重作为最优加权方案,能更进一步地减少三角形的最大形变以及形变量的波动.基于重心映射的参数化的代码与实现可参见:https://isaacguan.github.io/projects/tutte-embedding/.
| [1] |
郭风华, 张彩明, 焦文江. 网格参数化研究进展[J]. 软件学报, 2016, 27(1): 112-135. Guo Fenghua, Zhang Caiming, Jiao Wenjiang. Research progress on mesh parameterization[J]. Journal of Software, 2016, 27(1): 112-135. |
| [2] |
Lévy B. Constrained texture mapping for polygonal meshes[C]//Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 2001: 417-424.
|
| [3] |
Cheng Peng, Wang Jiaye, Miao Chunyan, et al. Constrained texture mapping via approximate Voronoi base domain[C]//Proceedings of Computer Graphics International 2018. New York: ACM Press, 2018: 19-22.
|
| [4] |
Qian Kun, Li Yinghua, Su Kehua, et al. A measure-driven method for normal mapping and normal map design of 3D models[J]. Multimedia Tools and Applications, 2018, 77(24): 31969-31989. DOI:10.1007/s11042-018-6207-y |
| [5] |
Biermann H, Martin I, Bernardini F, et al. Cut-and-paste editing of multiresolution surfaces[J]. ACM Transactions on Graphics, 2002, 21(3): 312-321. DOI:10.1145/566654.566583 |
| [6] |
Eyiyurekli M, Breen D E. Detail-preserving level set surface editing and geometric texture transfer[J]. Graphical Models, 2017, 93: 39-52. DOI:10.1016/j.gmod.2017.08.002 |
| [7] |
Lévy B. Dual domain extrapolation[J]. ACM Transactions on Graphics, 2003, 22(3): 364-369. DOI:10.1145/882262.882277 |
| [8] |
Kwok T H, Zhang Yunbo, Wang C C L. Efficient optimization of common base domains for cross parameterization[J]. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(10): 1678-1692. DOI:10.1109/TVCG.2011.115 |
| [9] |
Tutte W T. Convex representations of graphs[J]. Proceedings of the London Mathematical Society, 1960, 10(3): 304-320. |
| [10] |
Sheffer A, de Sturler E. Parameterization of faceted surfaces for meshing using angle-based flattening[J]. Engineering with Computers, 2001, 17(3): 326-337. DOI:10.1007/PL00013391 |
| [11] |
Sheffer A, Lévy B, Mogilnitsky M, et al. ABF++:fast and robust angle based flattening[J]. ACM Transactions on Graphics, 2005, 24(2): 311-330. DOI:10.1145/1061347.1061354 |
| [12] |
Lévy B, Petitjean S, Ray N, et al. Least squares conformal maps for automatic texture atlas generation[J]. ACM Transactions on Graphics, 2002, 21(3): 362-371. DOI:10.1145/566654.566590 |
| [13] |
Hormann K, Greiner G. MIPS: an efficient global parametrization method[M]//Laurent P J, Schumaker L L, Sablonniere P. Curve and Surface Design: Saint-Malo 1999. Nashville: Vanderbilt University Press, 2000: 153-162.
|
| [14] |
Fu Xiaoming, Liu Yang, Guo Baining. Computing locally injective mappings by advanced MIPS[J]. ACM Transactions on Graphics, 2015, 34(4): 71. |
| [15] |
Lipman Y. Bounded distortion mapping spaces for triangular meshes[J]. ACM Transactions on Graphics, 2012, 31(4): 108. |
| [16] |
Schüller C, Kavan L, Panozzo D, et al. Locally injective mappings[J]. Computer Graphics Forum, 2013, 32(5): 125-135. DOI:10.1111/cgf.12179 |
| [17] |
Sawhney R, Crane K. Boundary first flattening[J]. ACM Transactions on Graphics, 2017, 37(1): 5. |
| [18] |
Sawhney R. geometry-processing-js[EB/OL]. (2018-03-11)[2018-08-30]. https: //geometrycollective.github.io/geometry-processing-js/.
|
| [19] |
Mäntylä M. An introduction to solid modeling[M]. New York: Computer Science Press, 1988.
|
| [20] |
Kettner L. Using generic programming for designing a data structure for polyhedral surfaces[J]. Computational Geometry, 1999, 13(1): 65-90. DOI:10.1016/S0925-7721(99)00007-3 |
| [21] |
张应中, 谢馥香, 罗晓芳, 等. 采用半边编码的三角网格拓扑数据结构[J]. 计算机辅助设计与图形学学报, 2016, 28(2): 328-334. Zhang Yingzhong, Xie Fuxiang, Luo Xiaofang, et al. A topological data structure using coding of half-edges for triangle meshes[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(2): 328-334. DOI:10.3969/j.issn.1003-9775.2016.02.016 |
| [22] |
Taubin G. A signal processing approach to fair surface design[C]//Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1995: 351-358.
|
| [23] |
Meyer M, Desbrun M, Schröder P, et al. Discrete differential-geometry operators for triangulated 2-manifolds[M]//Hege H C, Polthier K. Visualization and Mathematics Ⅲ. Heidelberg: Springer, 2003: 35-57.
|
| [24] |
Floater M S. Mean value coordinates[J]. Computer Aided Geometric Design, 2003, 20(1): 19-27. |
| [25] |
Rivara M C. Mesh refinement processes based on the generalized bisection of simplices[J]. SIAM Journal on Numerical Analysis, 1984, 21(3): 604-613. DOI:10.1137/0721042 |
| [26] |
管焱然, 管有庆. 基于OpenCV的仿射变换研究与应用[J]. 计算机技术与发展, 2016, 26(12): 58-63. Guan Yanran, Guan Youqing. Research and application of affine transformation based on OpenCV[J]. Computer Technology and Development, 2016, 26(12): 58-63. |
| [27] |
Sorkine O, Cohen-Or D, Goldenthal R, et al. Bounded-distortion piecewise mesh parameterization[C]//Proceedings of the Conference on Visualization'02. Washington, D. C.: IEEE Computer Society, 2002: 355-362.
|




