2. 国防科技大学 信息通信学院, 西安 710106
考虑到实际分布式存储系统中存在热度不同的文件,构造了一种基于非均匀故障保护的分组修复码(GRC-NFP),可对热文件和高故障概率节点提供更高等级保护,并降低多故障节点修复的磁盘读取开销.在文件冷热分组后,用所存目标节点故障概率表征数据块故障概率,并排序,存入长度依次递增的多个数据分组,并生成组编码块.性能分析和实际系统部署结果表明,与里德-所罗门码和分组修复码相比,GRC-NFP可在存储开销较小的条件下拥有较高的容错能力和较低的修复局部性,并且使热文件能够受到更有效地保护.系统部署下较少的编码和故障修复时间进一步证明了GRC-NFP的可行性.
2. College of Information and Communication, National University of Defense Technology, Xi'an 710106, China
Considering that there are files with different heat in actual distributed storage systems, a class of group repairable codes based on non-uniform fault protection (GRC-NFP) is proposed. GRC-NFP provides higher protection for hot files and nodes with high fault probability, and reduces the disk I/O overhead for repairing multiple failed nodes. Specifically, after hot and cold grouping, the fault probabilities of data blocks are represented and sorted by that of the stored target nodes. Data blocks are stored into multiple data groups with increasing lengths, and group encoded blocks are further generated. Performance analysis and actual system deployment showed that GRC-NFP had higher fault tolerance and lower repair locality under less storage overhead compared with Reed-Solomon codes and group repairable codes. Moreover, the hot files can be protected more effectively by adopting GRC-NFP. The fewer coding and fault repair time under system deployment further proved the feasibility of GRC-NFP.
随着互联网技术的发展,海量数据存储引起研究者的广泛关注.传统的数据存储方案已经不能适应当前海量数据的存储,分布式存储系统逐渐成为主流的数据存储方式.通过将数据存储在多个独立物理存储设备上,分布式存储系统不仅能分担存储负载,而且成本低廉,可扩展性高,适用当前的海量数据存储.在分布式存储系统中,通常利用存储冗余数据确保数据存储的可靠性. Hadoop分布式文件系统、Google文件系统等利用复制方式来保证数据存储的高可靠性[1-2],但需要存储多个文件副本,系统存储开销过大.相比于复制方式,纠删码策略有效降低了存储开销[3-4],但是在修复故障节点时需要下载整个文件大小的数据量,修复带宽开销过大. Wu等[5-7]指出,将网络编码技术应用于分布式存储系统,可有效降低数据修复过程中的带宽开销.基于该冗余方式,Dimakis等[8]提出再生码的概念,实现了存储开销和修复带宽开销之间的最佳折中.再生码可以极大地减少故障节点修复时的数据传输量,但是需要连接较多的存活节点,修复局部性较高.局部性修复编码(LRC, locally repairable codes)通过将存储节点分组并产生组编码块来降低故障节点修复时需要连接的节点数[9-11],在单节点故障时具有较好的修复局部性,但是在多节点故障时仍需连接较多存活节点.基于LRC,分组修复码(GRC, group repairable codes)在分组内生成多个组编码块,降低了多故障节点修复时需要读取的数据量[12].
上述冗余方案中,视所有节点故障概率相同.受磁盘物理参数的影响,存储系统中每个存储节点故障概率呈现出不均匀分布的特征.在分布式系统中根据“帕累托”原则,80%的访问集中在20%的文件中,这20%的文件称为热文件,剩余的文件则统称为冷文件. Chang等[13]将文件大小作为文件热度区分的标准,这显然对于目前的文件系统是不合理的. Yim等[14]指出热数据可以被有效地压缩,而冷数据因为被编码不能被有效压缩,故Kim等[15]利用文件的压缩比与特定数值的大小来判定文件热度,这种方法的缺点在于计算数据压缩比的开销很大.目前,针对高故障概率节点和冷热文件进行不同的等级保护,邓俊杰[16]利用分组思想将原始数据块分成长度不等的数据,分组并异或组内数据,生成一个组编码块,该方案可以对高故障概率节点进行高等级保护,但是是否可以有效保护热文件没有经过验证,并且在多节点故障时磁盘读取开销仍较大.
为此,为了对分布式存储系统中不同热度文件采取不同等级保护,在节点非均匀故障的基础上结合分组修复码,提出一种新的编码方案——非均匀故障保护的分组修复码(GRC-NFP, group repairable codes based on non-uniform fault protection).具体地,冷热文件划分完成后,将数据块按照目标存储节点故障概率进行排序,存入长度不等的数据分组中,并且根据故障概率生成数目不等的组编码块.理论分析和平台部署结果表明,该非均匀故障保护的分组修复码在提高热文件保护等级的同时确保节点故障的修复局部性始终小于分组修复码.与里德-所罗门码(RS codes,Reed-Solomon codes)相比,存储效率虽然无法达到最优,但优于分组修复码.实际平台下,编码时间较少的同时拥有高等级保护下的低故障恢复时间,证明了GRC-NFP的部署使得系统性能达到一定的提升.
1 分组修复码最大距离可分码(MDS codes, maximal distance separable codes)把大小为M的文件平均分为k个数据块,利用生成矩阵编码生成n=k+m个相同大小的编码块,并分别存放在分布式存储系统中的n个节点中.
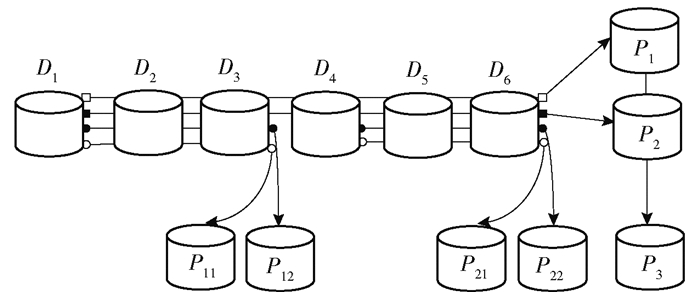
为了描述方便,称MDS码为原纠删码. GRC的具体构造如下:利用分组思想将原纠删码k个数据块分成L个组,记为Sl(l=1, 2, …L),组Sl包含kl个数据块.令原纠删码的全局编码块m=m0+m1保持原纠删码前m0个全局编码块不变,为每个组计算m1个组编码块,每个组的组编码块和原纠删码生成剩余m1个全局编码块的计算方法相同,生成矩阵中保留本组数据块编码系数,其余组全部置零.另外,将前m0个全局编码块记为Sl+1组,异或组内数据,生成组编码块.具体的(13, 6)GRC编码过程如图 1所示.
|
图 1 (13, 6)GRC编码示意图 |
如图 1所示,(13, 6)GRC将数据块D1~D6均分为两组S1和S2,每组生成m1=2个组编码块P11、P12和P21、P22,保留原纠删码m0=2个全局编码块P1和P2,并且将P1和P2视为一组生成组编码块P3.
2 非均匀故障保护的分组修复码 2.1 文件热度计算基于以上研究,将文件分为首次存储和非首次存储并分别使用不同计算方式定义其文件热度.
定义 1 定义文件的冷热分类C={Fcold, Fhot},其中C为文件冷热的假设. Fcold、Fhot分别指冷文件和热文件,并且包含了系统中的所有文件.
对于首次存储的文件,文件在指定计算周期内的热度为
| $ H = \sum\limits_{i = 1}^n {{v_i}} \chi $ | (1) |
其中:υi表示系统文件中数据块i的影响因子,χ表示数据块i在指定计算周期内的访问次数,n为文件中编码数据块的总数.若编码数据块i在指定计算周期内被用户访问,υi较大.
对于非首次存储的文件,使用数据块的重要特性引用量来表征文件热度,故文件在指定计算周期内的热度为
| $ H = \sum\limits_{t = 1}^r {{Z_t}} $ | (2) |
其中:Zt表示文件中数据块的引用量,r表示编码数据块总数.式(1)和式(2)中考虑了首次和非首次存储这一重要因素.接下来,利用阈值函数来判断文件的冷热性.参照强度不变性质设置阈值:
| $ f(\omega ) = {\left( {\prod \omega } \right)^{1/n}} $ | (3) |
其中:对于首次存储文件,ω表示用户在指定计算周期内对数据块的访问次数(ω=χ);对于非首次存储文件,ω表示用户在指定计算周期内的数据块引用量(ω=Zt);n表示文件中编码数据块总数,当文件热度计算值高于上述阈值则为Fhot;反之则为Fcold.
2.2 冷热文件的转化由于用户访问行为的不确定性,文件访问热度在一段周期之后可能发生变化,即文件热度为动态变化.因此,可根据以下过程来进行冷热文件之间的动态转换.
步骤 1 当文件按照首次存储与非首次存储计算热度后,建立冷文件访问量表P和热文件访问量表Q,其中P为存储后冷文件的集合,Q为存储后热文件的集合.
步骤 2 考虑文件热度的更新周期T,在更新周期后,重新计算文件热度,将Q中低于式(3)中阈值的文件重新存储在P中,同时将P中高于式(3)中阈值的文件重新存储在Q中,达到量表的动态更新.对于更新周期T的选取,若更新周期T选择较短,频繁更新文件热度的操作会影响系统对外整体性能,但若更新周期T选择较长,会弱化文件热度的变化.因此,综合考虑对于更新周期T的选择,当T为2个计算周期时,进行冷热文件的转化.
2.3 非均匀故障保护的分组修复码构造下面详细论述(k0, m0, L, τ)GRC-NFP的构造过程.原纠删码k个原始数据块分成L个数据分组,且第i(1≤i≤L)个数据分组存储容量为k0+2(i-1),即第i个数据分组可存储k0+2(i-1)个数据块.根据数据块目标存储节点的故障概率从高到低排序,第1个数据分组放入故障概率最高,即最易故障的k0个数据块;第2个数据分组放入次易故障的k0+2个数据块;按此类推,第L个数据分组放入最不易故障的k0+2(L-1)个数据块.
保持原纠删码后m0个全局编码块不变,分别记为Pi+L-m1(m1≤i≤m).对于故障概率大于τ的μ个高故障数据分组,根据MDS码分别生成m1个组编码块Pli(1≤i≤m1, 1≤l≤μ),只需将除本组之外的其余组数据置零,则m=m0+m1.组编码块Pli(1≤i≤m1, 1≤l≤μ)是原纠删码剩余m1个全局编码块在每个数据分组的投影.对于故障概率小于τ的L-μ个低故障数据分组,分别异或组内数据块生成一个组编码块Pi(μ≤i≤L).将m0个全局编码块作为Sl+1组,生成组编码块Pi+L+m0.编码公式表示为
| $ {P_{i + L + {m_0}}} = \sum\limits_{j = L + 1}^{L + {m_0}} {{P_j}} $ | (4) |
| $ {{P_i} = \sum\limits_{j = 1 + \sum\limits_{n = 1}^{i - 1} {\left[ {{k_0} + 2(n - 1)} \right]} }^{\sum\limits_{n = 1}^i {\left[ {{k_0} + 2(n - 1)} \right]} } {{D_j},\mu < i \le L} } $ | (5) |
| $ {{P_{i + L - {m_1}}} = \sum\limits_{j = 1}^k {{g_{ij}}} {D_j},{m_1} < i \le m} $ | (6) |
| $ {{P_{li}} = \sum\limits_{j = 1 + k - \sum\limits_{n = 1}^L {\left[ {{k_0} + 2(n - 1)} \right]} }^{\sum\limits_{n = 1}^l {\left( {{k_0} + 2(n - 1)} \right]} } \quad {g_{ij}}{D_j},1 \le i \le {m_1},1 \le l \le \mu } $ | (7) |
基于上述构造过程,可得总编码块数n=μm1+L-μ+m0+1+
| $ \frac{n}{{\sum\limits_{i = 1}^L {{k_i}} }} = \frac{{L + \left( {{m_1} - 1} \right)\mu + {m_0} + 1 + \sum\limits_{i = 1}^L {{k_i}} }}{{\sum\limits_{i = 1}^L {{k_i}} }} $ | (8) |
根据式(8),选取不同的k0值可以影响编码的存储效率.由上述定义可知,将高故障概率数据节点放入小分组中,显而易见,小分组的数据可用性高一些.数据可用性是指某些存储节点故障时,数据块能成功修复的概率.小分组中的数据块数目少,在拥有相同组编码块数目的情况下,小分组中保存的冗余信息就多一些,能够成功恢复的概率就高一些.所以,决定小分组中数据块数目的参数k0对于文件整体的可靠性具有一定影响.
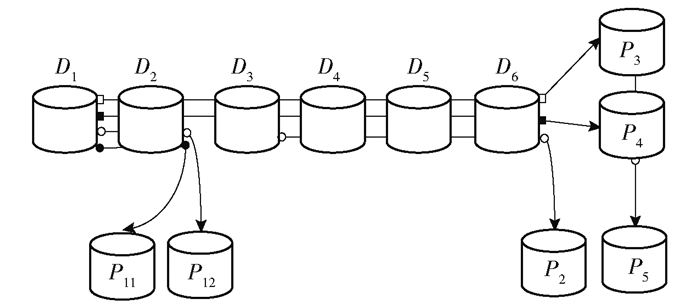
下面以图 2为例说明GRC-NFP的具体编码过程.为表示一般性,τ取0.2.
|
图 2 (2, 2, 2, 0.2)GRC-NFP编码示意图 |
(2, 2, 2, 0.2)GRC-NFP的编码过程及生成矩阵表示为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{C}} = \mathit{\boldsymbol{GD}} = \\ \left[ {\begin{array}{*{20}{c}} {}&{}&{{I_6}}&{}&{}&{}\\ {{g_{71}}}&{{g_{72}}}&0&0&0&0\\ {\$ {g_{81}}}&{{g_{82}}}&0&0&0&0\\ 0&0&1&1&1&1\\ {{g_{91}}}&{{g_{92}}}&{{g_{93}}}&{{g_{94}}}&{{g_{95}}}&{{g_{96}}}\\ {{g_{10,1}}}&{{g_{10,2}}}&{{g_{10,3}}}&{{g_{10,4}}}&{{g_{10,5}}}&{{g_{10,6}}}\\ {{g_{91}} + {g_{10,1}}}&{{g_{92}} + {g_{10,2}}}&{{g_{93}} + {g_{10,3}}}&{{g_{94}} + {g_{10,4}}}&{{g_{95}} + {g_{10,5}}}&{{g_{96}} + {g_{10,6}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{D_1}}\\ {{D_2}}\\ {{D_3}}\\ {{D_4}}\\ {{D_5}}\\ {{D_6}} \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{l}} {{D_1}}& \cdots &{{D_6}}&{{P_{11}}}&{{P_{12}}}&{{P_2}}&{{P_3}\;\;\;{P_4}\;\;\;{P_5}} \end{array}} \right]^{\rm{T}} \end{array} $ | (9) |
(2, 2, 2, 0.2)GRC-NFP将D1~D6数据块非均匀划分成2个数据分组,(D1, D2)为第1个数据分组,该分组数据块故障概率大于0.2,在组内生成m1=2个组编码块. (D3, D4, D5, D6)为第2个数据分组,该分组数据块失效概率小于0.2,在组内异或生成一个组编码块.保留原纠删码的全局编码块P3和P4,将P3、P4视为一个分组生成组编码块P5.
2.4 采用GRC-NFP的分布式文件存储由于CPU运算速度一直在急剧增长,然而与CPU相比,磁盘I/O速度仍然落后约6个数量级,使磁盘操作成为系统的主要性能瓶颈.在访问文件时,磁盘寻道时间通常是I/O延迟的主要部分.对于小于一个磁盘块的文件,它仍然需要一个磁盘块,占用的空间比它需要得多.这不仅会导致I/O操作过多,而且还会浪费磁盘空间.故文件分组是减少磁盘I/O延迟的一种有效方法.文件分组是一种通过将相关文件紧密放在磁盘上来减少I/O查找时间的方法.笔者将文件自适应地分为多个小文件分组,在小文件分组中对数据块使用GRC-NFP进行纠删保护.
图 3为自适应分组编码示意图.当文件需要进行存储时,根据是否是首次存储进行冷热判断,判断完成后为减少磁盘I/O延迟对文件进行自适应分组,每个小文件分组使用GRC-NFP进行编码,编码完成后存储在系统中供用户访问.

|
图 3 自适应分组编码示意图 |
按照上述的GRC-NFP构造方法将原始文件存储到分布式存储系统中的n个节点中,下文所述数据块故障为存储数据块的节点故障.本节主要讨论GRC-NFP的故障节点修复问题.
3.1 故障节点的不同等级保护分析GRC-NFP可以为高故障概率节点提供更高等级保护.假设图 1所示(13, 6)GRC中的(D1, D2, D3)分组以及该组的组编码块P11和P12全部故障.这种情况下是无法修复的,因为含有3个数据块信息的全局编码块只有P1和P2,无法从2个方程组中解出3个未知量.若(2, 2, 2, 0.2)GRC-NFP中(D1, D2)分组以及D3、P11和P12全部故障是可以进行数据修复的,这时由于P2的存在可以先进行D3的修复,然后利用P3和P4两个全局编码块便可以解出D1和D2.这样所有故障的数据块都可以修复完成.将所有2个编码方案中5个节点同时故障的情况列举出,(13, 6)GRC中第1分组不能修复率为2.4%,(2, 2, 2, 0.2)GRC-NFP中第1分组不能修复率仅为1%.由此可见,GRC-NFP可以有效提高对高故障概率节点的保护等级.
3.2 多节点故障修复定理 1 GRC-NFP最多能容忍λ=(μm1+L-μ+m0+1)个数据块和组编码块同时故障.
证明 编码块为数据块的冗余数据,编码块的数目也就是包含的冗余数据块数目.故编码方案中生成的编码块个数为该方案的容错能力.根据GRC-NFP的构造过程,在前μ数据分组中,每组生成m1个组编码块,因此在前μ组可以容忍μm1个数据块和组编码块故障.对后L-μ个数据分组,每组仅有1个组编码块,故可以容忍L-μ个数据块和组编码块在数据分组内故障.并且,存在m0个全局编码块和由全局编码块生成的一个组编码块.故GRC-NFP最多能容忍λ=(μm1+L-μ+m0+1)个数据块和组编码块同时故障.证毕.
对于(n, k)MDS码,根据故障数据块数目可以直接判断该故障情况是否可以成功修复.若故障数据块数目小于n-k则可以修复;否则无法修复.但是对于GRC-NFP来说,由于全局编码块m0和组编码块m1的存在使得可以有组内修复和全局修复2种修复.组内修复指利用组编码块进行修复,全局修复指利用全局编码块进行修复.换句话说,也就是无法根据故障块数目进行直接判断.即使故障块数目不大于λ,也有可能无法进行修复.由编码方案将故障情况分为编码块故障和数据块与编码块同时故障.在编码块故障情况下,只需根据GRC-NFP编码规则重新进行编码即可.故主要讨论另外一种故障情况的修复.
针对单数据块故障,由于组编码块的存在,使得所有单一数据块故障都能修复.所以,重点讨论2个及多个故障块的修复.在数据块和编码块同时故障的情况下,当故障块数目不大于λ时进行修复.整体修复原则是先在组内修复后在全局修复,以期尽可能降低修复开销,最后在全局修复使修复条件发生变化之后再进行组内修复.
当分布式存储系统采用GRC-NFP来存储数据,故障节点的具体修复过程包括以下步骤.
步骤 1 进行数据分组内修复,判断每个数据分组内数据块故障数目ε和未发生故障的组编码块数目φ.若ε≤φ,则进行数据分组内修复;若ε>φ,则等待进行全局修复.
步骤 2 对于无法在数据分组内修复的数据块进行全局修复.计算未故障的全局编码块与组编码块(处于故障数据块所在分组)数之和,若小于剩余无法修复的数据块数,则无法进行全局修复;反之,则利用未故障的全局编码块与组编码块(处于故障数据块所在分组)可以修复剩余的故障数据块.
步骤 3 由于在步骤2中全局修复完成后可能会使修复条件发生变化,若在步骤2中可以完成全局修复,则再进一步进行数据分组内修复.重复步骤1过程,利用步骤1、步骤2中已经修复好的数据块去修复未修复完成的编码块.若只有数据块故障,则修复过程只进行步骤1和步骤2.
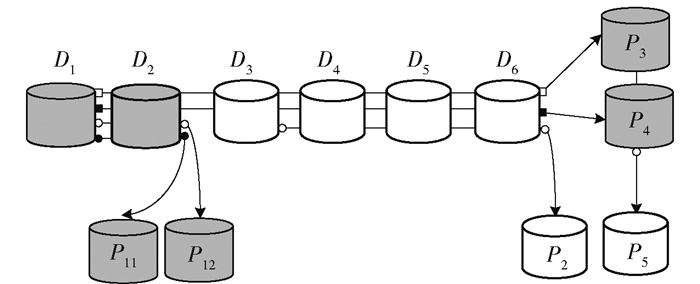
如图 4所示,深色数据块代表故障数据块.在进行修复时,首先进行数据分组内修复.第1数据分组故障数据块数目4大于未故障组编码块数目0,该组无法在数据分组内修复,而第2数据分组没有故障块不需要进行修复.全局编码块所在的分组故障块数目2大于未故障组编码块数目1,P3与P4均无法修复.其次,全局修复剩余的数据块.由于第1数据分组数据块故障的数目2大于未故障的全局编码块与组编码块(故障数据块所在分组)数目之和0,故无法进行全局修复.故得出结论在该故障情况下无法成功修复.
|
图 4 (2, 2, 2, 0.2)GRC-NFP码无法修复故障示意图 |
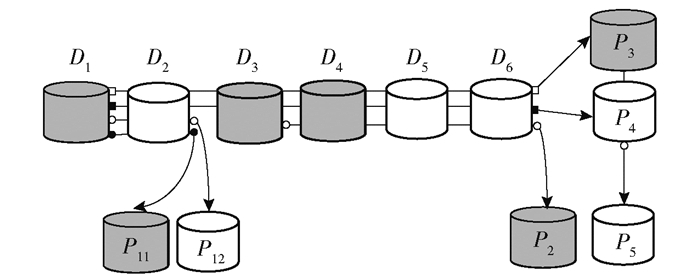
图 5中深色数据块同样代表故障数据块.在进行修复时,首先进行组内修复.第1数据分组故障数据块数目1不大于未故障组编码块数目1,该组可以在数据分组内修复.而第2分组的故障数据块数目2大于未故障组编码块数目0,所以无法进行数据分组内修复. P3可以通过P4和组编码块P5进行组内修复.其次,全局修复剩余的数据块.由于第2分组数据块故障的数目2等于未故障的全局编码块与组编码块(故障数据块所在分组)数目之和2,故D3、D4可以通过P3和P4进行修复.最后再进行组内修复,利用式(2)中修复完成的数据块可以成功修复P2.故得出结论:在该故障情况下可以成功修复.
|
图 5 (2, 2, 2, 0.2)GRC-NFP成功修复故障示意图 |
下面主要讨论非均匀故障保护的分组修复码GRC-NFP的存储开销、文件可靠性和修复局部性,并与现有的RS码和GRC进行比较.
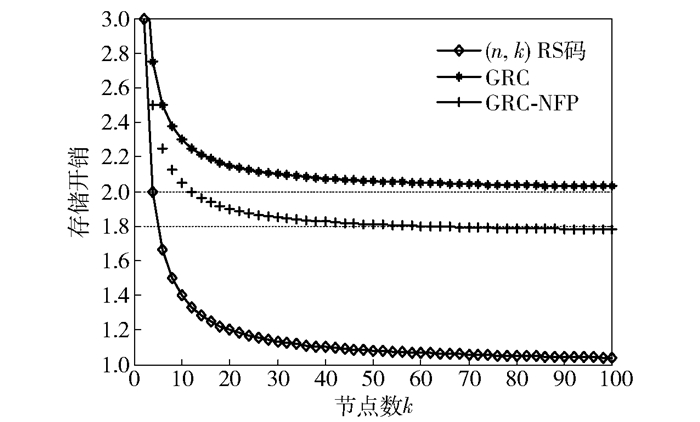
4.1 存储开销存储开销定义为编码后编码块存储空间与原始数据块存储空间的比值大小. (n, k)RS码将k个数据块利用生成矩阵编码生成n个编码块,因此(n, k)RS码的存储开销为n/k;根据GRC构造过程得总编码块数k+m0+Lm1+1,故GRC存储开销为(k+m0+Lm1+1)/k;根据式(9),GRC-NFP的存储开销为[k+L+(m1-1)μ+m0+1]/k,
|
图 6 存储开销对比 |
因为GRC码和GRC-NFP码均不满足MDS性质,相比RS码没有达到最优的存储开销. 图 6中,RS码的存储开销随着k的增大而减小,达到了最优的存储开销. GRC-NFP和GRC的存储开销随着k增大而减小,且GRC-NFP的存储开销整体小于GRC的存储开销.
4.2 文件可靠性利用成功修复故障节点的比率来衡量GRC-NFP的文件可靠性.若可以成功修复的比率越高,则文件的可靠性越高.在k0和故障节点数目取值后,计算GRC-NFP的不可成功修复概率即可知可成功修复概率.取k0=10时,总编码块数n=28.当故障节点数为4时,总可能的故障情况数目为C284,根据GRC-NFP中故障节点修复原则,统计不可修复的情况数目为C124+C123×3+C121×4+C122×5.故不可成功修复概率为0.075,可成功修复概率为0.925,其余不同k0和故障节点数目情况下同理.仿真过程中,取L=2, μ=1, m0=m1=2.
图 7给出了分组规模k0分别取2、10和20时,采用GRC-NFP的文件可靠性.故障节点数在3以内时,所有故障情况都可以成功修复. k0=2时,可成功恢复节点故障的概率都在0.9以上,随着k0的增加,当k0=10和k0=20时,可成功恢复节点故障的概率均小于k0=2时的恢复概率.当故障节点数为5时,相比k0=2的情况下降0.2左右,且k0=20可恢复故障概率小于k0=10的可恢复故障概率.因此,对于存储系统中的冷热文件,通过分组规模k0的选择可以提供不同等级保护.

|
图 7 不同k0对文件可靠性的影响 |
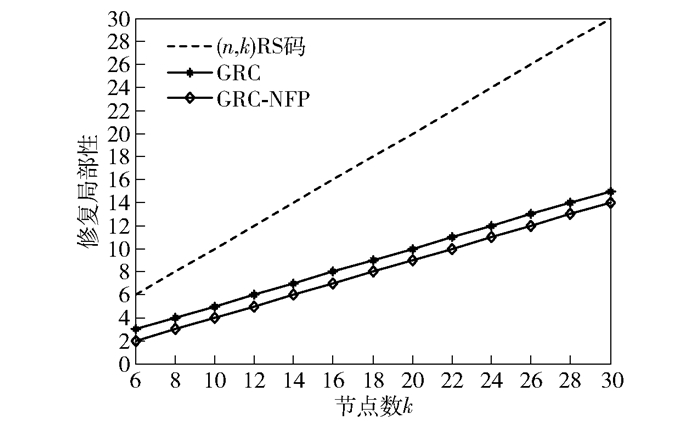
修复局部性为修复故障节点时需读取的磁盘数目,即磁盘读取开销.这里主要讨论单节点、两节点以及三节点故障时的修复局部性.为使故障修复都在一个数据分组里,取GRC和GRC-NFP中m1=3,并且在三节点故障时GRC-NFP中节点数目从8开始取值.当三节点以内故障时,(n, k)RS码需要连接k个节点来修复故障节点,即修复局部性为k;GRC至少需要连接kl个节点来修复故障节点,修复局部性为kl(kl=k/L);GRC-NFP关注高故障概率节点的修复局部性,前μ组内出现单个故障节点时需要至少连接k0+2(i-1) (1≤i≤μ)个节点来修复故障节点,修复局部性为k0+2(i-1) (1≤i≤μ).这里取L=2, β=1进行以下比较.
图 8给出了各种编码方案的修复局部性对比. (n,k)RS码的修复局部性随k呈线性增长. GRC和GRC-NFP相比RS码的修复局部性显著减少,并且GRC-NFP相比GRC的修复局部性更小.系统中数据节点数k=6时,(2, 2, 2, 0.2)GRC-NFP在D1、D2两节点故障的情况下,需读取2个数据块P11和P12.相比同样情况下,(13, 6)GRC需读取3个数据块D1、P11和P12,磁盘读取开销减小了1.在高故障概率数据节点修复占主要修复情形下,GRC-NFP可以有效降低多节点故障修复时的磁盘读取开销.这对于节点数目较大的存储系统故障节点的快速修复具有重要意义.
|
图 8 修复局部性对比 |
通过与RS码和GRC的分析与对比可得,在存储开销方面,在同样不满足MDS性质的情况下,GRC-NFP的存储开销要小于GRC,并且GRC-NFP的修复局部性要优于RS码与GRC. GRC-NFP以相比RS码少量的存储开销换取了较优的修复局部性和数据可靠性.
4.4 实验平台仿真结果采用FastDFS开源的轻量级分布式文件系统验证所提编码的性能,具体进行编码时间开销及故障恢复时间的实验.该系统服务器的配置为Intel(R) Corn(TM) i5-3337U 1.80 GHz,操作系统为RHEL7(Linux内核3.10.0),FastDFS采用C/S(服务端/客户端)模式,整体框架为使用虚拟机(8 GB内存和1 024×4 MHz)作为跟踪服务器与存储服务器,并设置客户端.每台虚拟机需装有nginx进行连接通信,并通过配置服务脚本设置为开机自启.
实验 1 存储服务器中设置节点n=13,并分别部署(10, 6)RS码、(13, 6)GRC码以及(2, 2, 2, 0.2)GRC-NFP.在节点中数据块大小分别为4、8、16 MB的情况下,统计部署这3种码分别需要的时间,为保证可靠性,取5次实验数据计算平均值.如图 9所示,(2, 2, 2, 0.2)GRC-NFP所需编码时间最少,比(13, 6)GRC码平均减少14%,(10, 6)RS码所需时间平均最多.

|
图 9 编码时间对比 |
从编码矩阵角度考虑3种编码的计算复杂度. (10, 6)RS码编码算法基于有限域GF(28),基础运算为gxjDk(7≤x≤10, 1≤j, k≤6),编码块为k=6个基础运算的线性组合. GRC由于分组的存在,组编码块所需的基础运算为RS码编码块的一半. GRC-NFP不仅存在组编码块,低故障数据分组中组编码块的基础运算为异或运算,减少了有限域上基础运算的操作,故编码时间较GRC和RS码有所减少.
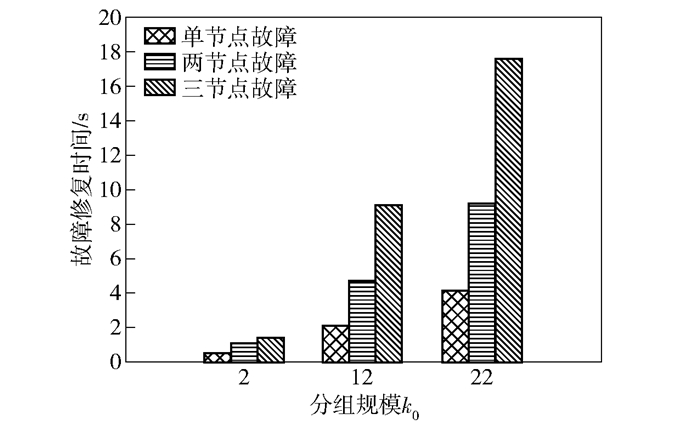
实验 2 考虑分组规模k0与故障修复时间之间的关系.故障修复时间直接影响系统整体性能.存储服务器中设置节点n=13, 节点存储容量为128 MB,分组规模k0分别取2、10和20时,分别统计故障节点均能被修复的情况下(单节点、两节点以及三节点故障)所需修复时间.同样,为保证可靠性,取5次实验数据计算平均值.如图 10所示,在分组规模k0取值依次增加的情况下,节点故障修复时间同样呈增加趋势,这是因为GRC-NFP的高等级保护机制是通过分组中所存数据块个数调节的,修复故障节点需顺序连接每个分组中数据块与所需编码块,k0的增加意味着所需连接数据块个数的增加.
|
图 10 不同k0对故障修复时间的影响 |
通过实验1和实验2的实验结果可知,部署该码后系统的性能良好,较少的编码时间与高保护等级下的低修复时间,使得用户可以安全可靠地上传访问文件.
5 结束语构造了一种基于非均匀故障保护的分组修复码.考虑到实际分布式存储系统中用户访问文件的不均衡性,通过分组规模的选择为热文件提供高于冷文件的保护.将高概率节点中的数据存入不同数据分组中,并生成数目不等的组编码块,实现保护高概率节点的同时降低了磁盘读取开销.理论分析与系统部署实验结果表明,相比RS码与GRC,GRC-NFP拥有较小存储开销的同时修复局部性最小,并且可以提高热文件的保护等级,同时拥有较小的编码时间和故障修复时间,可以更好地适应系统.
| [1] |
Shahabinejad M, Khabbazian M, Ardakani M. An efficient binary locally repairable code for Hadoop distributed file system[J]. IEEE Communications Letters, 2014, 18(8): 1287-1290. DOI:10.1109/LCOMM.2014.2332491 |
| [2] |
Ghemawat S, Gobioff H, Leung S T. The Google file system[J]. ACM SIGOPS Operating Systems Review, 2003, 37(5): 29-43. DOI:10.1145/1165389.945450 |
| [3] |
Lee O T, Kumar S D M, Chandran P. Erasure coded storage systems for cloud storage-challenges and opportunities[C]//3rd International Conference on Data Science and Engineering (ICDSE). Cochin: IEEE Press, 2016: 52-58.
|
| [4] |
Li J, Li B. Erasure coding for cloud storage systems:a survey[J]. Tsinghua Science and Technology, 2013, 18(3): 259-272. |
| [5] |
Wu Y. Existence and construction of capacity-achieving network codes for distributed storage[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(2): 277-288. DOI:10.1109/JSAC.2010.100217 |
| [6] |
Koetter R, Medard M. An algebraic approach to network coding[J]. ACM Transactions on Networking, 2003, 11(5): 782-795. DOI:10.1109/TNET.2003.818197 |
| [7] |
Ahlswede R, Cai N, Li S Y R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216. DOI:10.1109/18.850663 |
| [8] |
Dimakis A G, Godfrey P B, Wu Y, et al. Network coding for distributed storage systems[J]. IEEE Transactions on Information Theory, 2010, 56(9): 4539-4551. DOI:10.1109/TIT.2010.2054295 |
| [9] |
Oggier F, Datta A. Self-repairing homomorphic codes for distributed storage systems[C]//2011 Proceedings IEEE INFOCOM. Shanghai: IEEE Press, 2011: 1215-1223.
|
| [10] |
Gopalan P, Huang C, Simitci H, et al. On the locality of codeword symbols[J]. IEEE Transactions on Information Theory, 2012, 58(11): 6925-6934. DOI:10.1109/TIT.2012.2208937 |
| [11] |
Papailiopoulos D S, Dimakis A G. Locally repairable codes[C]//2012 IEEE International Symposium on Information Theory Proceedings (ISIT). Cambridge: IEEE Press, 2012: 2771-2775.
|
| [12] |
林轩. GRC:一种适用于多节点失效的高容错低修复成本纠删码[J]. 计算机研究与发展, 2014, 51(S): 172-181. Lin Xuan. GRC:a high fault tolerant low repair cost erasure code for multi-node failures[J]. Journal of Computer Research and Development, 2014, 51(S): 172-181. |
| [13] |
Chang L P. Hybrid solid-state disks: combining heterogeneous NAND flash in large SSDs[C]//Proceedings of the 13th ACM International Conference on Asia and South Pacific Design Automation Conference. Seoul: IEEE Press, 2008: 428-433.
|
| [14] |
Yim K S, Bahn H, Koh K. A flash compression layer for smart media card systems[J]. IEEE Transactions on Consumer Electronics, 2004, 50(1): 192-197. DOI:10.1109/TCE.2004.1277861 |
| [15] |
Kim K, Jung S, Song Y H. Compression ratio based hot/cold data identification for flash memory[C]//2011 IEEE International Conference on Consumer Electronics. Las Vegas: IEEE Press, 2011: 33-34.
|
| [16] |
邓俊杰.云存储中基于非均匀保护策略的纠删码技术研究与实现[D].长沙: 湖南大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10532-1018023279.htm
|


