针对车载网匿名认证的安全与效率问题,运用双线性对理论,提出一个基于身份的车载网批量匿名认证方案.通过车载单元的防篡改装置与可信中心协同完成车辆的身份匿名和消息的签名,进一步增强方案的安全性,同时减轻可信中心的负载;通过批量验证,提高车载网匿名认证效率.安全性和效率分析结果表明,所提方案不仅满足匿名性、不可伪造性和不可否认性等安全特性,而且具有更好的时间复杂度和空间复杂度.仿真结果显示,所提方案在有效性和可行性方面均取得了较好的效果.
For the security and efficiency of anonymous authentication in vehicular networks, an identity-based anonymous authentication scheme for vehicular networks is proposed by using bilinear pairing theory. The security of the scheme is further enhanced and the load of the trusted center is reduced by collaborating between the tamper-proof device of the onboard unit and the trusted center, the efficiency of the anonymous authentication of the onboard network is improved by batch verification. Security and efficiency analysis show that the scheme not only satisfies the security characteristics of anonymity, unforgeability and non-repudiation, but also has better time complexity and space complexity. The simulation results show that the scheme has certain advantages in both effectiveness and feasibility.
车载网(VANET,vehicular network)是一种以车辆为节点的特殊移动自组织网络(MANET,mobile Ad hoc network)[1].由于应用场景及无线通信模式影响, 车载网易受隐私、合谋、伪造等方面的安全攻击[2].为解决车载网中安全与隐私问题,国内外学者做了大量研究,并取得一系列成果. Sun等[3]提出一种基于身份单车辆认证的车载网隐私安全系统方案. Lee等[4]设计一种车载网群测试批量认证的方案(TSBV-GT,toward a secure batch verification with group testing for VANET),车辆真实身份易被泄露. Bayat等[5]提出一种车载网批量安全认证方案(SA-BV,secure authentication scheme for VANETs with batch verification),在安全性方面有所提高,然而,算法设计复杂,因此方案计算成本较高. Liu等[6]提出一种高效的车载网批处理匿名身份验证协议(EAA-BO,efficient anonymous authentication protocol using batch operatious for VANETs),该协议无法抵抗合谋攻击. Azees等[7]提出一种基于条件隐私的高效匿名认证保护方案,该方案签名过程的空间复杂度和通信复杂度较高. Vijayakumar等[8]提出一种计算有效的车载网隐私保护匿名双向批量认证方案(EAAP,EAA with conditional privacy-preserving scheme for vehicular Ad hoc networks),该方案存在重放攻击风险.
鉴于现有方案存在的不足之处,笔者提出了一个基于身份的车载网批量匿名认证方案(IBAA,identity-based batch anonymous authentication scheme for vehicular network),该方案具有较强的隐私安全和较高的执行效率,同时通信开销有所降低.
1 预备知识 1.1 双线性对设G1和G2分别为q阶加法循环群和q阶乘法循环群(q是一个大素数),双线性对[9]e:G1×G1→G2满足如下性质:
1) 双线性,即∀P1, P2∈G1和∀a, b∈Zq*,满足e(aP1, bP1)=e(P1, P2)ab.
2) 非退化性,即∃P1,P2∈G1,使得e(P1, P2)≠1.
3) 可计算性,即∀P1,P2∈G1,存在有效的算法计算e(P1, P2).
4) 对称性,即∀P1,P2∈G1,满足e(P1, P2)=e(P2, P1).
1.2 安全基础椭圆曲线密码体制(ECC,elliptic curve cryptography)是一种基于代数曲线的公钥密码系统.设p为一大素数,Fp为模p的有限域,在Fp上的椭圆曲线方程式表示为
| $ {y^2} = {x^3} + cx + d $ | (1) |
其中:c, d∈Fp且满足4c2+27d3≠0mod p.设x, y∈Fp,若(x, y)满足式(1),则(x, y)为曲线E上的点,用E(Fp)表示曲线E上无穷远点∞及所有点集合,或记为Ep(c, d).
椭圆曲线离散对数难题(ECDLP,elliptic curve discrete logarithm problem)是椭圆曲线密码体制的基础.给定椭圆曲线上阶为g的一点P及该曲线上另一点Q,确定整数x∈Zq*,0≤x≤q-1,使得Q=xP∈G1是困难的.
计算Diffie-Hellman难题(CDHP,computational Diffie-Hellman problem)可以有效解决密钥配送问题.给定xP, yP∈G1,其中x, y∈Zq*是未知整数,计算Q=xyP∈G1是困难的.
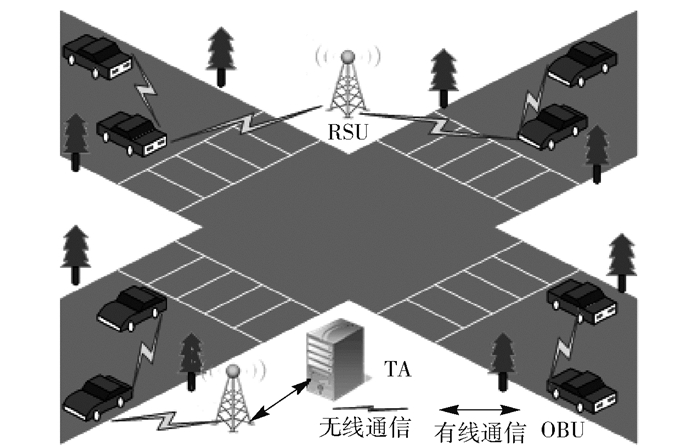
1.3 车载网模型如图 1所示,车载网模型主要由3部分实体构成:可信中心(TA,trusted authority)、路侧单元(RSU,road side unit)和车载单元(OBU,on board unit).每个实体的功能如下.
|
图 1 车载网模型 |
1) 可信中心.指车载网系统权威可信管理中心,负责系统安全参数生成和发布、车辆注册、管理、追踪等功能,通常部署在交通管理部门.
2) 路侧单元.部署在路旁的车辆通信基站,通过DSRC协议[10]与车辆通信,负责车辆网络接入、管理中心信息发布、车辆交互信息的发送与接收等.
3) 车载单元.指装配在车辆中的无线通信单元,负责秘钥存储、信息加/解密、通过DSRC协议与路侧单元通信.
2 本文方案 2.1 初始化阶段第 1 步 可信中心生成2个阶均为q的循环群G1和G2,其中G1是为循环群,G2为乘法循环群,P和Q为G1的2个生成元;随机选取r∈Zq*作系统的私钥,生成公钥Ppub=rP.
第 2 步 可信中心随机选取3个安全Hash函数h:{0, 1}*→G1,h1:{0, 1}*→Zq*,h2:{0, 1}→Zq*.
第 3 步 可信中心将r作为系统的私钥秘密保存,将Ppub作为系统参数公开.
2.2 身份匿名阶段第 1 步 新车辆用户向可信中心提交UserName、E-mail、IDNumber等相关身份信息请求注册.
第 2 步 可信中心根据车辆用户信息进行登记审核,并为该车辆用户分配用户名Ridi和口令Pwdi,其中,Ridi∈G1.将Ridi、Pwdi和r装载到车辆的防篡改装置(TPD,tamper proof device)中.
第 3 步 用户输入用户名Ridi和口令Pwdi,TPD验证用户输入信息的有效性,若用户输入信息与装载信息一致,则通过验证,执行第4步;否则,终止匿名操作.
第 4 步 TPD随机选取σi∈Zq*,计算车辆的匿名身份Id={I1i, I2i},并将{σi, Idi}保存在TPD中,其中,I1i=σiP,I2i=Ridi+h(σiPpub).
2.3 签名阶段第 1 步 TPD提取系统私钥r,计算车辆私钥Ki=rh1(ID1i‖ID2i),并将其与{σi, Idi}一起存储在TPD中.
第 2 步 车辆用户输入需要签名的消息Mi到TPD.
第 3 步 TPD收到消息Mi后,计算
| $ {S_i} = \left( {{K_i} + {\sigma _i}{h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)} \right)Q $ | (2) |
其中Ti为消息签名的时间戳.
第 4 步 TPD将{Idi, Mi, Si, Ti}作为消息Mi的签名传递给车辆.
2.4 验证阶段根据验证消息数量的不同,分为单车辆验证和批量验证2种情况.
1) 单车辆验证
第 1 步 由于消息具有时效性,当车辆或路侧单元收到验证消息{Idi, Mi, Si, Ti}后,引入不等式ΔT≥Tr-Ti,其中ΔT为预测误差时延,Tr为接收消息的时间.
第 2 步 判断该等式,若不等式成立,则签名消息有效;若该式不满足,则签名消息无效,终止验证,丢弃该消息.
第 3 步 验证下面等式是否成立:
| $ e\left( {{S_i}, P} \right) = e\left( {{h_1}\left( {I_1^i\left\| {I_2^i} \right.} \right){P_{{\rm{pub}}}} + {h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)I_1^i, Q} \right) $ | (3) |
若式(3)成立,则签名消息合法,接收消息n;否则,拒收该消息.
2) 批量验证
第 1 步 类似单车辆验证,每收到签名消息{Idi, Mi, Si, Ti},首先对其进行时效性验证,即判断ΔT≥Tr-Ti是否成立,若成立,则为有效签名;否则,放弃该签名消息.
第 2 步 路侧单元为n个批量待验证的签名消息分别随机选取n个矢量{V1, V2, …, Vn},其中Vi∈[1-2t],t取值为一小整数.
第 3 步 路侧单元计算:
| $ {U = e\left( {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{V}}_i}} {S_i}, P} \right)} $ | (4) |
| $ {B = e\left( {\left( {\left( {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{V}}_i}} {h_1}\left( {I_1^i\left\| {I_2^i} \right.} \right)} \right){P_{{\rm{pub}}}} + } \right.} \right.}//{\left. {\left. {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{V}}_i}} {h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)I_1^i} \right), Q} \right)} $ | (5) |
判断
将认证方案记为ξ,攻击者记为A,F0和F1在游戏中代表 2个诚实车辆用户.
定义 1 匿名游戏
第 1 步 攻击者通过密钥生成算法得到公私钥对(Ppub, r),系统公共参数{G1, G2, P, Q, q, e, Ppub, h( ), h1( ), h2( )}.
第 2 步 攻击者A选取2个不同的消息m0、m1.
第 3 步 随机选择位b∈{0, 1},然后将mb和m1-b秘密发送给F0和F1.此时,b对攻击者保密.
第 4 步 F0和F1分别执行本文的签名方案ξ.
第 5 步 如果F0和F1输出2个有效的签名τb和τ1-b,分别与消息m0和m1相对应,则把τb和τ1-b按照随机顺序发送给攻击者A;否则,返回无效符号⊥给攻击者.
第 6 步 攻击者A对τb签名进行分析,输出关于b的猜想b′,b′∈{0, 1},当b′=b时,攻击者A赢得游戏.
本文方案定义攻击A赢得游戏的优势Vξ, Alink(A)=|2Pr[b′=b]-1|,则Pr [b′=b]表示b′=b的概率.
定理 1 如果攻击者者A不可能在多项式时间内使用签名方案在匿名游戏中以不可忽略的概率赢得游戏,则该方案满足匿名性.
C作为在定义1中匿名游戏的挑战者,如果在第5步中收到的是⊥,说明A获得的是无效信息,得到正确b的概率为
考虑到另一种情况,假设攻击者A在执行完本文方案的签名后得到了2个签名,分别为(S0, T0, Id0, M0)和(S1, T1, Id1, M1).设j∈{0, 1},j表示该签名方案的一个实例,其中(σj, P, Kj)表示交互过程中的参数.为了证明方案的匿名性,对于{(S, T, Id, M)}∈{(S0, T0, Id0, M0), (S1, T1, Id1, M1)}和任意的参数(σj, Kj),I1i=σjP,I2i=Ridi+h(σjPpub),Kj=rh1(I1i‖I2i),j∈{0, 1}.最后可得
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{S_i} = \left( {{K_j} + {\sigma _j}{h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)} \right)Q = \\ r{h_1}\left( {{\sigma _j}P\left\| {R_{{\rm{id}}}^i} \right. \oplus h\left( {{\sigma _j}{P_{{\rm{pub}}}}} \right)} \right) + {\sigma _j}{h_2}\left( {{M_i}\left\| T \right.} \right)Q = \\ \;\;\;\;\;\;\;\;\;\;\;r{h_1}\left( {I_1^i\left\| {I_2^i} \right.} \right) + {\sigma _j}{h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)Q \end{array} $ | (6) |
因此
| $ \begin{array}{l} e(S, P) = e\left( {{K_j} + {\sigma _j}{h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)Q, P} \right) = \\ e\left( {\left( {r{h_1}\left( {I_1^i\left\| {I_2^i} \right.} \right) + {\sigma _j}{h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)Q} \right), P} \right) = \\ \;\;\;e\left( {{h_1}\left( {I_1^i\left\| {I_2^i} \right.} \right){P_{{\rm{pub}}}} + {h_2}\left( {{M_i}\left\| {{T_i}} \right.} \right)I_1^i, Q} \right) \end{array} $ | (7) |
定理 2 如果CDHP难题在多项式时间内求解是困难的,本文方案在随机预言模型下可抵抗选择消息攻击,即满足不可伪造性.
证明 设攻击者为A,挑战者为C. ∀x, y∈Zq*,x, y未知,已知P∈G1,(P, xP, yP),挑战者C求解xyP,即挑战CDHP难题.假设攻击者A能够伪造有效消息签名{Idi, Mi, Si, Ti},C执行如下步骤.
1) 初始化阶段. C重置系统公共参数:Ppub=xP, Q=yP,然后将(Ppub, Q)发送给攻击者A;同时,构造并保存3个列表Lh、Lh1和Lh2.
2) h询问阶段. C构造一个记录形如元组〈α,βh〉的列表Lh,初始状态为空.当C收到来自A关于消息α的询问时, C检查列表Lh是否存在记录〈α,βh〉,若存在,C回答βh;否则,C随机选择β′h∈Zq*,并将〈α,β′h〉添加到列表中,然后回答β′h.
3) h1查询阶段.挑战者C保持并维护记录形如元组〈I1i, I2i, βh1〉的列表Lh1,初始状态为空.当C收到来自于A带有(I1i, I2i)消息的询问时,C查询列表Lh1中是否存在元组〈I1i, I2i, βh1〉,若存在,C回答βh1;否则,C随机选择β′h1∈Zq*,并将〈I1i, I2i, β′h1〉添加到列表,然后,回答β′h1.
4) h2查询阶段.挑战者C保持并维护记录形如元组〈I1i, I2i, βh2〉的列表Lh2,初始状态为空.当C收到来自于A带有(Mi, Ti)消息的询问时,C查询列表中是否存在元组〈Mi, Ti, βh2〉,若存在,回答βh2;否则,C随机选择β′h2∈Zq*,并将〈Mi, Ti, β′h2〉添加到列表.然后,回答β′h2.
5) 签名询问阶段.挑战者C随机生成γi, hi, 1, hi, 2∈Zq*,I2i∈G1,计算Si=γiQ,I1i=(γiP-hi, 1Ppub)/hi, 2;将〈I1i, I2i, hi, 1〉和〈Mi, Ti, hi, 2〉添加到列表Lh1和Lh2中检查e(Si, P)
6) 输出阶段. A进行2次不同的询问后,在多项式时间内C会获得2个有效的签名{Ii, Mi*, Si, Ti}和{Idi, Mi*, Si*, Ti*},且Si=(γihi, 1+xhi, 2)Q,Si*=(γihi, 1+xhi, 2*)Q能够得到满足.从而C进行计算得(hi, 2-hi, 2*)-1(Si-Si*)=xQ=xyP,CDHP问题得以解决.但这与CDHP问题是困难的相矛盾,即本文方案满足不可伪造性.
3.1.3 不可否认性不可否认性又称抗抵赖性,即发生交通事故时,能够证据验证、解决纠纷和追究责任.当某个车辆存在恶意行为时,方案中的可信中心能够恢复恶意车辆的真实身份.车辆的匿名身份为Idi=(I1i, I2i),其中I1i=σiP,I2i=Ridi+h(σiPpub),可信中心通过私钥r计算I2i⊕h(rI1i)可以恢复该车辆的真实身份Ridi,即
| $ \begin{array}{*{20}{c}} {I_2^i \oplus h\left( {rI_1^i} \right) = I_2^i \oplus h\left( {{\sigma _i}rP} \right) = }\\ {I_2^i \oplus h\left( {{\sigma _i}{P_{{\rm{pub}}}}} \right) = R_{{\rm{id}}}^i} \end{array} $ |
若恢复出真实身份的车辆否认自己行为,方案基于小指数测试法[11],引入随机矢量V,车辆进行通信时,每个签名均加入不同标志矢量V,通过对签名消息进行批量验证,恶意车辆则无法抵赖,即满足不可否认性.
3.2 效率分析 3.2.1 计算复杂度本文方案计算复杂度仅与代表性TSBV-GT方案、SA-BV方案、EAA-BO方案、EAAP方案进行比较.定义Tpar为一次双线性对运算所需时间,Tmp-bp为双线性对上一次点乘运算所需时间,Tmp-ecc为椭圆曲线上一次点乘运算所需时间,Tmtp为哈希运算所需时间.各方案的计算复杂度对比如表 1所示.根据文献[12],使用Intel i7 4 GHz内存的处理器,在Windows 7环境下,应用MIRACL加密数据库运行安全的80 bit椭圆曲线上的循环子群,操作时间:Tpar=4.21 ms,Tmp-bp=1.71 ms,Tmp-ecc=0.44 ms,Tmtp=4.41 ms.
|
|
表 1 计算复杂度对比 |
表 1显示,单签名验证过程中,本文方案明显优于TSBV-GT方案和SA-BV方案,与EAA-BO方案所需时间持平,略差与EAAP方案.但在批量签名验证过程中,SA-BV方案、EAA-BO方案和EAAP方案所需要的时间与批量签名消息个数n成正比,IBAA方案和TSBV-GT方案所需时间与签名消息个数n无关,明显优于其他方案.
3.2.2 通信复杂度通信复杂度指通信中所需的通信量,即存储空间.一次完整车载网匿名认证方案的通信复杂度通常由消息的签名、假名和其他附加信息构成.如TSBV-GT方案,消息签名21 bit,假名42 bit,时间戳4 bit;SA-BV方案,签名消息42 bit,假名234 bit,时间戳4 bit;EAA-BO方案,消息签名53 bit,假名42 bit;EAAP方案,消息签名60 bit,假名40 bit,时间戳4 bit;本文方案,消息签名20 bit,假名40 bit,时间戳4 bit.如表 2所示,IBAA方案通信复杂度优于其他方案.
|
|
表 2 通信复杂度对比 |
实验在64位的Windows10操作系统、Intel i5 CPU处理器、4 GB内存、NS-2.35仿真软件和802.11a无线协议的环境下进行.设定模拟仿真区域面积为1 200 m×1 200 m,车辆节点数量在20~100之间,车辆行驶速度在0~108 km/h之间,车辆节点随机分布在仿真区域范围内的道路上.
仿真实验从平均消息延迟和平均消息丢失率来验证方案的有效性和可行性.平均消息延迟和平均消息丢失率分别用Tamd和Palr表示.
| $ {T_{{\rm{amd }}}} = \frac{{\sum\limits_{i = 1}^{{N_V}} {\sum\limits_{m = 1}^{N_m^i} {\left( {T_{s \to m}^i + T_{t \to m \to r}^i + T_{r \to v \to m}^i} \right)} } }}{{\sum\limits_{i = 1}^{{N_V}} {N_m^i} }} $ |
其中:NV为模拟区域中车辆个数,Nmi为车辆i发送消息数量,Ts→mi为车辆i对消息m的签名时间,Tt→m→ri为车辆i向路侧单元发送消息m的时间,Tr→v→mi为路侧单元对车辆i认证的时间.
| $ {P_{{\rm{alr }}}} = \frac{{\sum\limits_{i = 1}^{{N_V}} {N_m^i} - \sum\limits_{j = 1}^{{R_n}} {N_r^j} }}{{{R_n}\sum\limits_{i = 1}^{{N_V}} {N_m^i} }} $ |
其中:Rn为路侧单元的个数,Nrj为第j个路侧单元接收到消息的数量.
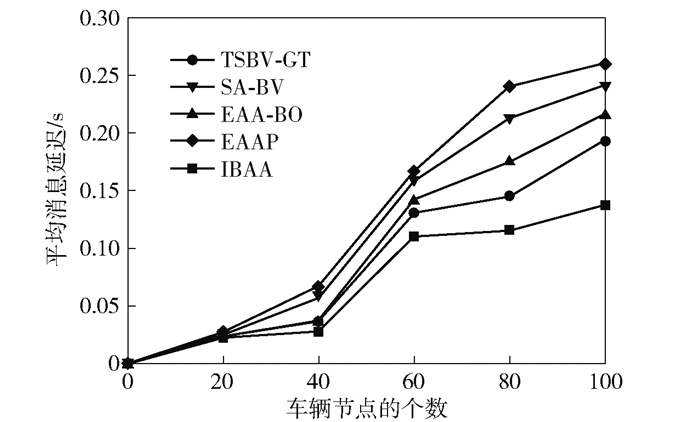
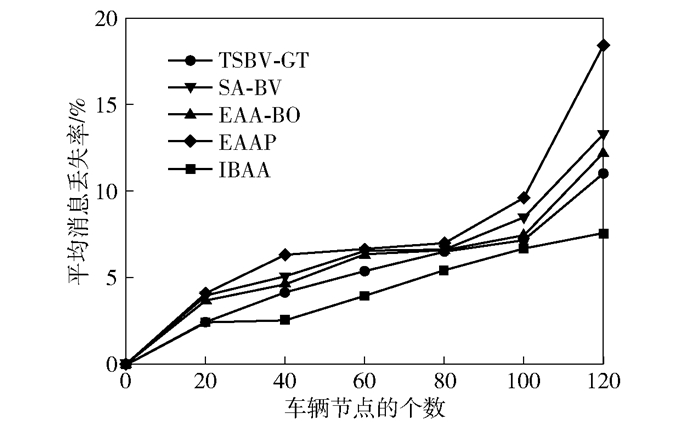
仿真结果如图 2和图 3所示.仿真结果显示,在平均消息延迟方面,当节点在0~60之间时,本文方案与其他方案相当,随着车辆节点数目的增加,本文方案明显优于其他方案;在平均消息丢失率方面,节点为0~20之间时,本文方案优于SA-BV方案、EAA-BO方案和EAAP方案,与TSBV-GT方案相当,随着车辆节点数目的增加,IBAA方案优于其他方案.
|
图 2 平均消息延迟与车辆节点数量的关系 |
|
图 3 平均消息丢失率与车辆节点数量的关系 |
针对车载网环境中的隐私保护和匿名认证效率问题,基于椭圆曲线上的双线性对性质和相关难题假设,提出了一种基于身份的批量匿名认证方案.车辆身份匿名和消息的签名由车载单元的防篡改装置协同可信中心共同完成,不仅增强了安全性,而且减轻了可信中心的计算负载.在随机预言模型下证明了本文方案的匿名性和签名的不可伪造性,分析了时间复杂度和空间复杂度,并在平均消息延迟和平均消息丢失率方面与现有方案进行仿真比较.本文方案在安全性、有效性和可行性方面均存在一定的优势.对于资源受限的车载网在交通领域中的应用具有重要的意义和价值.
| [1] |
Singh K, Saini P, Rani S, et al. Authentication and privacy preserving message transfer scheme for vehicular Ad hoc networks (VANETs)[C]//ACM International Conference on Computing Frontiers. (ACMICCCF2015). New York: ACM Press, 2015: 58.
|
| [2] |
Wang Shibin, Yao Nianmin. A RSU-aided distributed trust framework for pseudonym-enabled privacy preservation in VANETs[J]. Wireless Networks, 2019, 25(3): 1099-1115. |
| [3] |
Sun Jinyuan, Zhang Chi, Zhang Yanchao, et al. An identity based security system for user privacy in vehicular ad hoc networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2010, 21(9): 1227-1239. DOI:10.1109/TPDS.2010.14 |
| [4] |
Lee C C, Lai Y M. Toward a secure batch verification with group testing for VANET[J]. Wireless Networks, 2013, 19(6): 1441-1449. DOI:10.1007/s11276-013-0543-7 |
| [5] |
Bayat M, Barmshoory M, Rahimi M, et al. A secure authentication scheme for VANETs with batch verification[J]. Wireless Networks, 2015, 21(5): 1733-1743. DOI:10.1007/s11276-014-0881-0 |
| [6] |
Liu Yawei, He Zongjian, Zhao Shengjie, et al. An efficient anonymous authentication protocol using batch operations for VANETs[J]. Multimedia Tools and Applications, 2016, 75(24): 17689-17709. DOI:10.1007/s11042-016-3614-9 |
| [7] |
Azees M, Vijayakumar P, Deboarh L J. EAAP:efficient anonymous authentication with conditional privacy-preserving scheme for vehicular ad hoc networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(9): 2467-2476. DOI:10.1109/TITS.2016.2634623 |
| [8] |
Vijayakumar P, Chang V, Deborah L J, et al. Computationally efficient privacy preserving anonymous mutual and batch authentication schemes for vehicular ad hoc networks[J]. Future Generation Computer Systems, 2018(78): 943-955. |
| [9] |
Brezing F, Weng A. Elliptic curves suitable for pairing based cryptography[J]. Designs Codes and Cryptography, 2005, 37(1): 133-141. |
| [10] |
Tong Zhen, Lu Hongsheng, Haenggi M, et al. A stochastic geometry approach to the modeling of DSRC for vehicular safety communication[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(5): 1448-1458. DOI:10.1109/TITS.2015.2507939 |
| [11] |
Cui Jie, Zhang Jing, Zhong Hong, et al. An efficient certificateless aggregate signature without pairings for vehicular Ad hoc networks[J]. Information Sciences, 2018(451): 1-15. |
| [12] |
SHIM K A. CPAS:an efficient conditional privacy preserving authentication scheme for vehicular sensor networks[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1874-1883. DOI:10.1109/TVT.2012.2186992 |


