2. 桂林电子科技大学 广西自动检测技术与仪器重点实验室, 广西 桂林 541004
对于具有能量收集装置的基站,由于收集的能量具有随机性,为保证基站稳定运行,在智能电网作为基站能源补充的情况下,基于排队论和Lyapunov优化方法提出了基站非弹性能量需求和弹性能量需求2种情况下的动态能量管理算法.运用所提算法,基站可根据系统状态动态地选择在电价低时从智能电网适当购买能量存储在充电电池中,以备将来电价高且收集的能量不能满足需求时使用,从而减小基站的能耗成本.所提的动态能量管理算法复杂度低,不需要能量收集、基站能量需求、时变电价的先验统计信息.理论分析结果表明,所提算法可使基站的能耗成本无限接近最优值,且保证弹性能量需求情况下的时延不超过可容忍的期限.仿真结果验证了所提算法的有效性和电池容量大小对算法性能的影响.
2. Guangxi Key Laboratory of Automatic Detecting Technology and Instruments, Guilin University of Electronic Technology, Guangxi Guilin 541004, China
A dynamic energy management scheme of the energy harvesting base station powered by the smart grid with time-varying price is proposed. Specially, it was assumed that the base stations(BSs) were equipped with energy harvesting device, and the free energy collected by this device from renewable sources were stored in battery for BSs to use in future. Due to the randomness of energy harvest, smart grid was taken as a supplement of energy to ensure the stable operation of BSs. Based on queuing theory and Lyapunov optimization method, a dynamic energy management algorithm was proposed for BSs under two conditions of inelastic energy demand and elastic energy demand. Based on the proposed algorithm, BSs can dynamically choose to purchase energy from smart grid at low price and store it in battery for using at high price for reducing the energy cost of BSs. The proposed dynamic energy management algorithm has low complexity and does not need prior statistical information of energy collection, energy demand and time-varying price. The theoretical analysis showed that the proposed algorithm performed arbitrarily close to the optimal objective value, meanwhile, it ensured that the time delay did not exceed the tolerable time. Finally, simulation results showed the validity of the algorithm. And the effect of battery capacity on the performance of the algorithm was analyzed.
随着移动互联网的快速发展,在新型移动设备(智能手机、平板等)的驱动下,移动数据流量呈爆炸性增长,不断增长的数据速率导致大量的能量消耗,也给蜂窝网络运营商带来了高额的能耗成本[1-2].因此,如何降低蜂窝网络的能耗成本,同时满足用户日益增长的通信需求,是目前非常重要的技术和经济问题.
随着能量收集(EH, energy harvesting)技术的发展,具有EH功能的基站可从周边环境中收集能量自供电,从而节约传统能源,有效地降低了蜂窝网络的能耗成本[3-4].但由于EH受到天气等因素的影响,收集的能量具有间歇性和随机性,为保证基站稳定可靠的运行,电网可作为EH基站的候补能源.目前已有研究者对EH能源和传统电网混合供电模式的通信网络开展了研究[5-8],但其中传统电网的电价均为固定电价.近年来,电网正经历着从传统电网向智能电网的转变[2],新部署的智能电网、电力运行商使用时变电价来平衡电力消费者时变的负载[2, 7].
由于基站的能耗及智能电网的电价均是时变的,而EH受到天气等因素的影响,更是难于统计EH过程的概率分布,因此EH和智能电网混合供电下的蜂窝网络具有较高的随机性,而Lyapunov优化技术理论适用于随机过程统计特性难于预知(一般随机过程)条件下的优化研究. Rahbar、Xu、Liu等[6-10]运用Lyapunov优化方法研究了不同无线网络的资源管理方案,如移动蜂窝网络、D2D(device to device)网络、Wi-Fi,方案包括能量管理、功率分配、数据调度等方面,刘迪迪等[11]基于Lyapunov优化研究了蜂窝网络中基站间的能量协作算法,但这些研究中蜂窝网络的供电源一般为传统电网,均没有考虑智能电网供电和电价的时变特性.
不同于早期的工作[8-11],笔者研究了具有EH功能的基站在智能电网时变电价下的动态能量管理方案,基于智能电网的时变电价,提出了基站非弹性能量需求和弹性能量需求2种情况下的动态能量管理算法,目的是最小化基站的能耗成本.所提的动态能量管理算法复杂度低,不需要知道基站能量收集、能量需求及智能电网时变电价的先验统计信息.本研究为未来智能电网时变电价下的基站提供了具有一般性(不需要随机过程的统计信息)的能量管理方案,控制基站在电价低、充电供电价高且能量收集不足时使用,能有效降低蜂窝网络的能耗成本,同时加入了智能电网平滑时变负荷的激励措施,有利于智能电网的稳定.
1 建模和问题描述蜂窝网络中具有EH功能、智能电网作为补充能源的基站模型如图 1所示. EH装置能根据所处的环境釆用合适的能量收集方式收集能量,并将收集的能量存储在充电电池中供基站使用.基站和充电电池同时与智能电网相连,基站可直接从智能电网获取电量.此外,基站基于智能电网的时变电价,控制充电电池在电价低时从智能电网充电,以备电价高且能量收集不足时供基站使用.
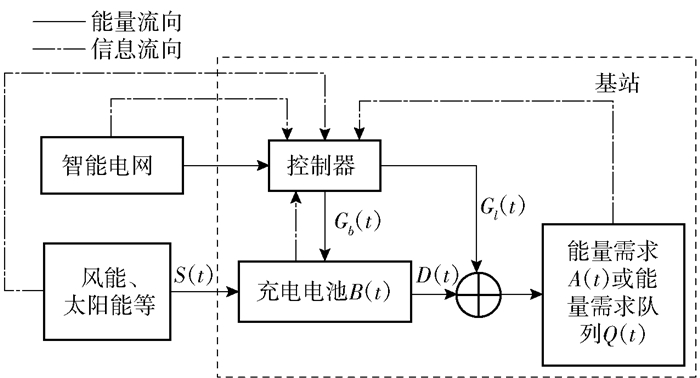
|
图 1 智能电网作为补充能源的EH基站模型 |
假设t时隙收集的能量为S(t),由于充电电池存储效率特性不完美,能量存储过程中会损失一部分能量,简化起见,S(t)为t时隙末实际存入电池中的能量,则有:0≤S(t)≤Smax ,Smax 为一个时隙内收集能量的最大值.本文的建模不同于文献[11],由于收集的能量是免费的,只要电池容量允许,尽可能将收集的能量全部存入电池,即存入的EH能量由电池的容量控制,而不再通过专门的控制器进行EH能量存入控制.
电池中t时隙的能量记为B(t),本研究中时隙间隔较小(为1 min),忽略充电电池的不理想特性(漏电等),电池能量B(t)可根据式(1)更新:
| $ B\left( {t + 1} \right) = B\left( t \right) - D\left( t \right) + S\left( t \right) + {G_b}\left( t \right) $ | (1) |
其中:D(t)为t时隙电池的放电量,即t时隙基站从电池获取的电量,对于∀t,0≤D(t)≤Dmax,Dmax为电池一个时隙的最大放电量;Gb(t)为t时隙电池从智能电网的充电量,0≤Gb(t)≤Gbmax,Gbmax为电池一个时隙从智能电网的最大充电量.电池容量的最大值为Bmax,在每个时隙显然有
| $ D\left( t \right) \leqslant B\left( t \right) \leqslant {B^{\max }} $ | (2) |
智能电网的电价是时变的,记为C(t),基于电网的时变电价,基站控制器可根据当前的能量需求、能量收集、电池容量以及电池中可用的能量等因素,动态地决策该时隙是否从智能电网购电以及购买多少能量Gb(t)给充电电池充电,以备将来电价高且收集的能量不能满足基站能量需求时使用,以降低基站的能耗成本.
笔者将基站的能量需求分为非弹性能量需求和弹性能量需求.非弹性能量需求是指基站的能量需求应立即满足,不允许有时延;而弹性能量需求是指基站允许需求的能量有一定的时延,如基站消耗能量用于传输文件数据,只要在一定时间内能满足用户要求即可[12].
假设t时隙基站的能量需求为A(t),基站从充电电池获取的能量为D(t),从智能电网购买Gb(t)存入电池中.此外,基站直接从智能电网获取的能量记为Gl(t),则t时隙基站从智能电网中购买的总能量为Gb(t)+Gl(t),每个时隙基站从电网能耗的成本为C(t)[Gb(t)+Gl(t)],优化的目标函数为
| $ \min :\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T E \left\{ {C(t)\left[ {{G_b}(t) + {G_l}(t)} \right]} \right\} $ | (3) |
该系统中充电电池中可用的能量、基站能量需求、能量收集的实时信息由基站直接监测;智能电网的时变电价通过无线信号传递给基站,智能电网中部署了信息通信的基础设施,可使上述组件之间能够进行信息收集和传递[12].
2 问题规划和求解基于上述模型,在基站能量需求、能量收集以及电价均为一般随机过程(概率分布未知)的情况下,通过动态地控制每个时隙的决策变量序列{D(t), Gb(t), Gl(t)},使基站在满足能量需求的前提下能耗成本最小.
2.1 非弹性能量需求及其求解基站t时隙的能量需求为A(t),若该需求为非弹性能量需求,应立即得到满足,因此基站从充电电池和智能电网获取的能量应满足:
| $ A\left( t \right) = D\left( t \right) + {G_l}\left( t \right) $ | (4) |
每个时隙基站从智能电网直接获取的最大能量为Glmax,0≤Gl(t)≤Glmax.
基站在非弹性能量需求情况下的问题规划如下:
| $ {P_1} = \mathop {\min }\limits_{D(t),{G_b}(t),{G_l}(t)} \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T E \left\{ {C(t)\left[ {{G_b}(t) + {G_l}(t)} \right]} \right\} $ | (5) |
约束:式(1)、式(4)
| $ D(t) \leqslant B(t) \leqslant {B^{\max }} $ | (6) |
| $ 0 \leqslant D(t) \leqslant {D^{\max }} $ | (7) |
| $ 0 \leqslant {G_b}(t) \leqslant G_b^{\max } $ | (8) |
| $ 0 \leqslant {G_l}(t) \leqslant G_l^{\max } $ | (9) |
式(5)为优化目标,其中E{C(t)[Gb(t)+Gl(t)]}表示基站能耗成本的期望,其物理含义为:通过控制每个时隙的决策变量D(t)、Gb(t)、Gl(t),最小化基站长期运行(T→∞)能耗成本期望的时间平均值.采用Lyapunov优化算法不需要任何系统状态的先验知识,就可以得到上述目标函数的最优解[13].
首先构造一个变量X(t):
| $ X(t) = B(t) - {V_1}{C^{\max }} - {D^{\max }} $ | (10) |
其中:V1为控制参数,Cmax为电价最大值,X(t)是用来确保提出算法满足电池电量约束条件(6).直观地,收集的能量尽可能全部存入电池.由于电池的容量有限,有可能造成收集能量浪费的,为确保上述问题可行,假设E[S(t)] < E[A(t)],这样在提出的算法中,通过合理调节参数V1使电池电量保持在合理范围:
| $ - {V_1}{C^{\max }} - {D^{\max }} \leqslant X(t) \leqslant {B^{\max }} - {V_1}{C^{\max }} - {D^{\max }} $ | (11) |
基于电池能量更新式(1),X(t)根据式(12)更新:
| $ X(t + 1) = X(t) - D(t) + S(t) + {G_b}(t) $ | (12) |
定义Lyapunov函数:
| $ \Delta L(X(t)) \triangleq E\{ L(X(t + 1)) - L(X(t))|X(t)\} $ | (13) |
将Lyapunov函数代入式(13)求解得到ΔL(X(t))的上界:
| $ \begin{array}{*{20}{c}} {\Delta L(X(t)) \leqslant \frac{1}{2}\max \left[ {{{\left( {G_b^{\max } + {S^{\max }}} \right)}^2},{{\left( {{D^{\max }}} \right)}^2}} \right] - } \\ {X(t)E\left[ {D(t) - S(t) - {G_b}(t)} \right]} \end{array} $ | (14) |
根据Lyapunov漂移函数的性质[13],最小化式(14)则能满足约束(6),因此规划问题式(5)~式(9)转化为式(15),同时受到式(4)和式(7)~式(10)的约束,即
| $ \min :\Delta L(X(t)) + {V_1}E\left\{ {C(t)\left[ {{G_l}(t) + {G_b}(t)} \right]|X(t)} \right\} $ | (15) |
s.t.约束式(4)、式(7)~式(10)
求解式(15),基于ΔL(X(t))的上界式(14),可得到
| $ \begin{array}{*{20}{c}} {\Delta L(X(t)) + {V_1}E\left\{ {C(t)\left[ {{G_l}(t) + {G_b}(t)} \right]|X(t)} \right\} \leqslant } \\ {{F_1} - X(t)E\left\{ {\left[ {D(t) - S(t) - {G_b}(t)} \right]|X(t)} \right\} + } \\ {{V_1}E\left\{ {C(t)\left[ {{G_l}(t) + {G_b}(t)} \right]|X(t)} \right\}} \end{array} $ | (16) |
其中:F1=
最小化式(15),即最小化每个时隙不等式(16)的右边,原问题可转化为
| $ \begin{array}{l} {P_2} = \min \sum\limits_{t = 1}^T {\left\{ {\left[ {{V_1}C(t) + X(t)} \right]{G_b}(t) + } \right.} \\ \left. {X(t)S(t) + \left[ {{V_1}C(t)} \right]{G_l}(t) - X(t)D(t)} \right\} \end{array} $ | (17) |
s.t.约束式(4)、式(7)~式(10)
求解问题P2,得到非弹性能量需求情况下动态算法如下:
1) 初始化:V1、T、B(1)、X(1)、Bmax.
2) 循环执行:
for t=1:1:T
检测系统状态X(t), C(t), A(t)
根据式(19)选择求解的控制决策,即
D(t), Gl(t), Gb(t)
if X(t)>-V1C(t)
Gb(t)=0;D(t)=min(B(t), A(t)); Gl(t)=A(t)-D(t);
else
Gb(t)=Gbmax; Gl(t)=min (A(t), Gmax l);
D(t)=A(t)-Gl(t);
end
分别根据式(1)、式(12)更新B(t), X(t)
end
2.2 非弹性能量需求动态算法性能分析定理 1 假设Glmax+Gbmax≥Amax,在时隙t∈{1, 2, 3, …, T}上任意常数V1满足0≤V1≤V1max,
| $ V_1^{\max } = \frac{{{B^{\max }} - {D^{\max }} - G_b^{\max } - {S^{\max }}}}{{{C^{\max }} - {C^{\min }}}} $ | (18) |
其中:Cmin为电介最小值,则上述算法有以下性质.
1) 队列X(t)在所有时隙都有界:经推导同前面式(11).
2) 如果S(t)、A(t)、C(t)在时隙上独立同分布,则在上述算法下平均成本的期望与最优解P1*的差不超过
| $ \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T E \left\{ {C(t)\left[ {{G_l}(t) + {G_b}(t)} \right]} \right\} \le P_1^* + \frac{{{F_1}}}{{{V_1}}} $ | (19) |
从定理1得出,队列X(t)随参数V1的增大而减小,基站的能耗成本(目标函数)随参数V1的增大更接近最优值P1*,通过调节参数V1可使目标函数值接近最优值P1*,所提算法求得的解随时间变化(T→∞)具有稳定性.由于同时要考虑充电电池中的实时电量应控制在合理的范围,所以要合理调节V1的值.
2.3 弹性能量需求及其求解基站t时隙的能量需求A(t)若为弹性能量需求,则允许有一定时延,这些能量需求存储在队列,以先进先出的方式被服务,只要该能量需求队列Q(t)中的任何能量需求的等待时间不超最大过时延要求Tmax即可.能量需求队列Q(t)根据以下公式更新:
| $ Q(t + 1) = \max \left\{ {Q(t) - D(t) - {G_l}(t),0} \right\} + A(t) $ | (20) |
为了保证Q(t)中所有能量需求的等待时间不超过最大时延Tmax,构造虚队列Z(t):
| $ Z(t + 1) \buildrel \Delta \over = \max \left[ {Z(t) - D(t) - {G_l}(t) + \varepsilon {1_{\{ Q(t) > 0\} }},0} \right] $ | (21) |
其中:1{Q(t)>0}为一个指示函数,当Q(t)>0时,则其取值为1;否则为0;ε为一个固定的正常数,是对虚队列积压的惩罚,相当于虚队列的到达过程,用于控制虚队列Z(t)的增长速度.在Q(t)>0的情况下,每个时隙到达ε,而虚队列和实队列的服务速率相同,这就可以保证如果队列Q(t)中有长期未被服务的数据,Z(t)就会增长.以下引理表明,如果可以控制参数以确保队列Q(t)和Z(t)具有有限的上界,那么就可保证Q(t)中所有能量需求都不超过最大时延.
引理 1 假设可以通过控制参数以确保在所有时隙t上有Q(t)≤Qmax和Z(t)≤Zmax,其中Qmax和Zmax是正常数,那么基站能量需求队列的最大时延为
| $ {T^{\max }} = \frac{{{Q^{\max }} + {Z^{\max }}}}{\varepsilon } $ | (22) |
引理1是根据文献[13]中的Lyapunov优化方法推导而得.根据引理1调整参数ε可改变基站能量需求队列的最大等待时延,使能量需求的等待时间不超过最大时延要求.
基站在弹性能量需求情况下的问题规划如下:
| $ {P_3} = \min \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T E \left\{ {C(t)\left[ {{G_b}(t) + {G_l}(t)} \right]} \right\} $ | (23) |
| $ {\rm{s}}.\;{\rm{t}}.\;\overline {Q(t)} < \infty ,\overline {Z(t)} < \infty $ | (24) |
约束式(1)、式(6)~式(9).
其中:
| $ {X_{{\rm{ela}}}}(t) \buildrel \Delta \over = B(t) - {\mathit{\Theta }^{{\rm{max}}}} - {D^{{\rm{max}}}} $ | (25) |
其中:Θmax为控制参数,Xela(t)根据以下式子更新:
| $ {X_{{\rm{ela}}}}(t + 1) = {X_{{\rm{ela}}}}(t) - D(t) + S(t) + {G_b}(t) $ | (26) |
求解方法同非弹性能量需求的方法,得到弹性能量需求情况下动态算法如下:
1) 初始化:V2、T、B(1)、Q(1)、Z(1)、Xela(1)、Bmax.
2) 循环执行:
for t=1:1:T
检测系统状态Q(t), Z(t), Xela(t), C(t), A(t)
求解的控制决策D(t), Gl(t), Gb(t),即
if Q(t)+Z(t)>V2C(t)
if Xela(t)>-V2C(t)
Gb(t)=0;D(t)=min (B(t), Q(t), Dmax );
Gl(t)=min (Q(t)-D(t), Gmax l);
elseif Xela(t)>-[Q(t)+Z(t)]
Gb(t)=Gbmax; D(t)=min (B(t), Q(t), Dmax );
Gl(t)=min (Q(t)-D(t), Gmax l);
else
Gb(t)=Gbmax; D(t)=0;
Gl(t)=min (Q(t), Gmax l);
end
else
if Xela(t)>-[Q(t)+Z(t)]
Gb(t)=0;Gl(t)=0;D(t)=min (B(t), Q(t), Dmax );
elseif Xela(t)>-V2C(t)
Gb(t)=0;Gl(t)=0;D(t)=0;
else
Gb(t)=Gmax b; Gl(t)=0;D(t)=0;
end
end
分别根据式(1)、式(20)、式(21)、式(26)更新B(t)、Q(t)、Z(t)、Xela(t).
end
2.4 弹性能量需求动态算法性能分析定理 2 假设Glmax≥max {Amax, ε},如果Q(1)=Z(1)=0,则当t∈{1, 2, 3, …, T}时,有参数0≤ε≤E{A(t)},0 < V2≤V2max,其中
| $ V_2^{\max } = \frac{{{B^{\max }} - {A^{\max }} - \varepsilon - {D^{\max }} - G_b^{\max } - {S^{\max }}}}{{{C^{\max }} - {C^{\min }}}} $ | (27) |
则上述算法有以下性质.
1) 在所有的时隙t中,队列Q(t)和Z(t)都有上确界:
| $ Q(t) \le {V_2}{C^{\max }} + {A^{\max }} $ | (28) |
| $ Z(t) \le {V_2}{C^{\max }} + \varepsilon $ | (29) |
且Q(t)+Z(t)≤Θmax ,Θmax =V2Cmax +Amax+ε.
2) 基站能量需求队列中任何能量需求的最大时延Tmax 为
| $ {T^{\max }} = \frac{{2{V_2}{C^{\max }} + {A^{\max }} + \varepsilon }}{\varepsilon } $ | (30) |
3) 若给定ε,且ε≤E{A(t)},基于笔者提出的算法,基站要从智能电网额外获得的能量满足自身能量需求,其成本期望的平均值与最优值P2*的差值不超过
| $ \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T {\left\{ {C(t)\left[ {{G_l}(t) + {G_b}(t)} \right]} \right\}} \le P_2^* + \frac{{{F_2}}}{{{V_2}}} $ | (31) |
其中:F2为常数,
| $ \begin{array}{*{20}{c}} {{F_2} = \frac{1}{2}\left\{ {\max \left[ {{{\left( {G_b^{\max } + {S^{\max }}} \right)}^2},{{\left( {{D^{\max }}} \right)}^2}} \right] + } \right.}\\ {\max \left[ {{{\left( {{D^{\max }} + G_l^{\max }} \right)}^2},{\varepsilon ^2}} \right] + }\\ {\left. {\max \left[ {{{\left( {{D^{\max }} + G_l^{\max }} \right)}^2},{{\left( {{A^{\max }}} \right)}^2}} \right]} \right\}} \end{array} $ |
从定理2得知,数据等待时延随参数V2的增大而增大,智能电网能耗的成本(目标函数)随参数V2的增大更接近最优值P2*.通过调节参数V2可使目标函数值接近最优值P2*,但是能量需求等待时间可能会变长,所以V2应适当取值.为了减小最大等待时延Tmax ,ε的取值应当尽可能大,但要满足ε≤E{A(t)},如果给定E{A(t)},则可使ε=E{A(t)}.
基于Lyapunov提出的2种情况下的能量管理方案,只需根据检测每时隙的能量收集、能量需求及电价情况,然后做出相应决策,算法容易实现.由算法的性能分析可知,所提算法可使优化目标向最优值无限渐近,算法的解随时间变化具有稳定性.此外,该算法不需要知道这些随机过程的统计分布知识,具有一般性和普适性,并且复杂度低.算法的复杂度仅与时隙数呈线性增长.
3 仿真结果采用的算法不受一般随机过程概率分布的影响.为了评估所提算法的性能,方便演示仿真结果,假设基站能量收集和能量需求过程分别服从不同均值的泊松分布.智能电网的电价根据一天中不同时段的负荷大小而变化,假设一天的电价变化有2个用电高峰期,对应2个电价高峰,电价在0.5~1.8元之间波动,时隙间隔取1 min,一天共划分为1 440个时隙,这里考虑的时段为60天(86 400个时隙),电价每天的变化趋势均重复第1天的电价模型.
根据实际调查情况,蜂窝通信网络中一个中性基站平均每个月电费约为1 100元,结合目前蜂窝网络中基站实际能量的消耗情况和市场上充电电池的容量范围,参数设置见表 1.
|
|
表 1 仿真参数设置 |
首先验证基站非弹性能量需求情况下提出的实时能量管理算法的有效性,为更好地评估提出的算法,将其与直接购买法进行对比.直接购买法是指基站不存储智能电网的能量,若收集并存储的免费能量不能满足能量需求,不管电价高低,直接从智能电网购买能量需求不足的部分. 2种算法下基站能耗成本的对比如图 2所示,此时V1=200.从图 2可看出,在60天末,基于直接购买法,不具备EH功能基站的能耗成本为1 802.90元,具备EH功能基站的能耗成本为454.53元,而基于Laypunov优化算法基站的能耗成本为262.78元,提出的算法比目前不具备EH功能且直接购买能量的基站节约1 540.12元,平均每月节省约770.06元.提出的算法之所以节约成本,原因是该算法基于电价可根据能量需求和收集情况以及电池容量和当前可用的能量决策购买多少能量存入电池以备基站使用.

|
图 2 非弹性能量需求基站能耗成本的对比 |
为评估电池容量Bmax 对所提算法的影响,给出了非弹性能量需求下电池容量对基站能耗成本的影响,如图 3所示.从图 3可以看出,电池越大,基站能耗成本越小.原因有两方面:一是电池容量较大时,收集的免费能量能尽可能多地存储在电池中,不造成浪费;二是电价较低时,电池容量较大则能存入更多的低电价能量,以备基站在电价高且能量收集不足时使用,从而节约成本.由于电池容量越大,电池的成本越高,此外基站的最大能量需求有限,因此基站在选取储能设备容量时可根据电池成本和带来的效益折中选择.

|
图 3 电池最大容量对基站能耗成本的影响 |
图 4给出了基站能量需求在非弹性和弹性不同情况下所提算法的对比.在相同的参数下,弹性能量情况下基站的能耗成本低于非弹性能量需求情况的成本,原因是基站可以不必立即被响应弹性能量需求,从而等待使用收集的免费能量或者低电价能量,也就是用时延换取更低的成本.
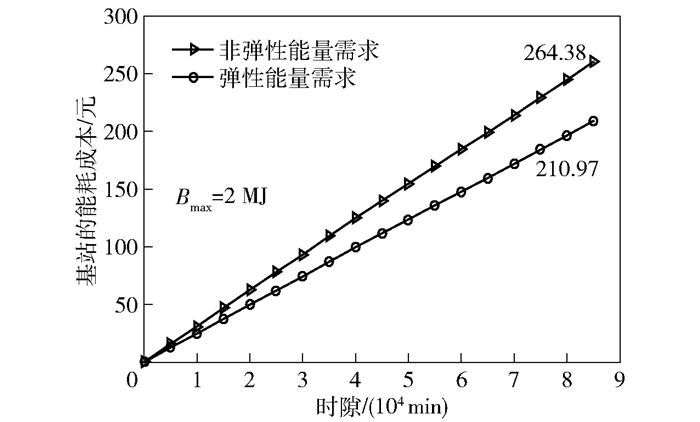
|
图 4 非弹性和弹性能量需求下所提算法性能的对比 |
图 5为EH能量平均值大小不同的3种情况下不同算法的能耗成本直方图,其中EH能量平均值依次增加,纵坐标为基站累计60天的能耗成本.从图 5可以看出:①弹性能量需求下的Lyapunov优化算法在每种EH情况下,从智能电网的能耗总成本均最低;② EH能量的平均值越大,可用的免费能量越多,基站的能耗成本越低.
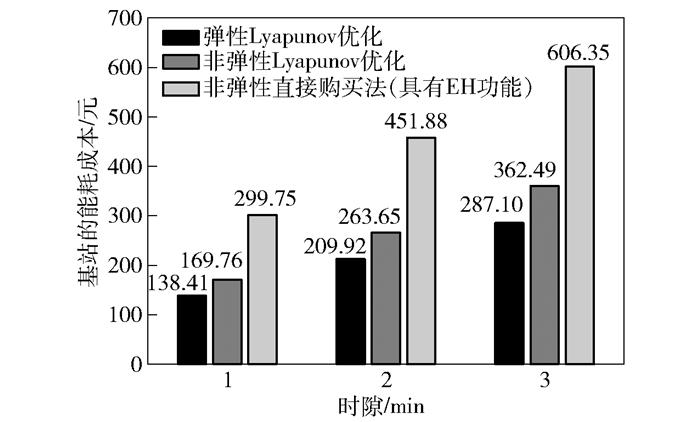
|
图 5 不同情况下各算法基站能耗成本 |
为方便观察弹性能量需求情况下所提算法给队列带来的时延,图 6给出了基于Lyapunov优化算法和最后期限消耗算法下60天内到达的能量需求等待时延分布以及基站能耗成本对比.最后期限消耗算法是指基站在指定期限内只消耗存储在电池中的能量,若最后期限还不能满足基站的能量需求,则从智能电网购买能量满足能量需求.笔者设置的最大期限为20个时隙,在这种参数设置下,采用Lyapunov优化算法基站能耗成本比最后期限消耗算法下的低,约节省242.2元,如图 6所示.采用Lyapunov优化算法能量需求平均等待7.9个时隙,而最后期限消耗算法平均等待19.5个时隙,绝大部分的能量需求等待到最后2个时隙才被满足,所以基于Lyapunov优化所提的算法在能量需求等待时延和性能上都有明显的优势.

|
图 6 弹性能量需求下两种算法的性能和时延对比 |
笔者研究具有EH功能的基站在智能电网时变电价下的动态能量管理方案,基于智能电网的时变电价,提出了基站非弹性能量需求和弹性能量需求两种情况下的动态能量管理算法,目的是最小化基站的能耗成本.所提的动态能量管理算法复杂度低,无需知基站能量收集、能量需求和智能电网时变电价的先验统计信息,理论分析表明,该算法可使基站的能耗成本无限接近最优值,且保证在弹性能量需求情况下的时延不超过时延要求.此外,分析了电池容量大小对所提算法性能的影响.本研究为未来智能电网时变电价下的基站提供了具有一般性(不需要随机过程的统计信息)的能量管理方案,通过控制基站在电价低时充电,供电价高且能量收集不足时使用,能有效降低蜂窝网络的能耗成本,同时加入了智能电网平滑时变负荷的激励措施,有利于智能电网的稳定.
| [1] |
Liu D, Lin J, Wang J, et al. Dynamic power allocation for a multiuser transmitter with hybrid energy sources[J]. EURASIP Journal on Wireless Communications and Networking, (2017), 2017, 203. |
| [2] |
Xu J, Duan L, Zhang R. Energy group buying with loading sharing for green cellular networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 786-799. DOI:10.1109/JSAC.2016.2544603 |
| [3] |
Mura Y, Minowa H, Nakayama Y, et al. A study of stand-alone power supply for "small green base station" with photovoltaic system[C]//2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA). New York: IEEE Press, 2017: 1172-1174.
|
| [4] |
Zhang H, Huang S, Jiang C, et al. Energy efficient user association and power allocation in millimeter-wave-based ultra dense networks with energy harvesting base stations[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 1936-1947. DOI:10.1109/JSAC.2017.2720898 |
| [5] |
Ulukus A, Yener E, Erkip O. Energy harvesting wireless communications:a review of recent advances[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 360-381. DOI:10.1109/JSAC.2015.2391531 |
| [6] |
刘迪迪, 马丽纳, Jiang Frank. 混合供电发射机的能量调度和自适应功率算法[J]. 北京邮电大学学报, 2017, 40(6): 103-108. Liu D D, Ma L N, Jiang F. Energy scheduling and adaptive transmission power algorithm for a transmitter with hybrid energy sources[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(6): 103-108. |
| [7] |
Fang X, Miasra S, Xue G, et al. Smart grid -the new and improved power grid:a survey[J]. IEEE Communications Surveys & Tutorials, 2012, 14(4): 944-980. |
| [8] |
Rahbar K, Xu J, Zhang R. Real-time energy storage management for renewable integration in microgrid:an off-line optimization approach[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 124-134. |
| [9] |
Guo Y, Pan M, Fang Y. Optimal power management of residential customers in the smart grid[J]. IEEE Transactions on Parallel and Distributed Systems, 2012, 23(9): 1593-1606. DOI:10.1109/TPDS.2012.25 |
| [10] |
Yu H, Cheung M H, Huang L, et al. Power-delay tradeoff with predictive scheduling in integrated cellular and Wi-Fi networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 1-22. DOI:10.1109/JSAC.2016.2550838 |
| [11] |
刘迪迪, 林基明, 王俊义, 等. 蜂窝网络中能量收集基站的能量协作算法[J]. 上海交通大学学报, 2018, 52(3): 365-372. Liu D D, Lin J M, Wang J Y, et al. The algorithm of energy cooperation in cellular networks with energy-harvesting base stations[J]. Journal of Shanghai Jiaotong University, 2018, 52(3): 365-372. |
| [12] |
Navid R, Behrouz M, Vahid S M, et al. Game-theoretic approaches for energy cooperation in energy harvesting small cell networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 7178-7194. DOI:10.1109/TVT.2017.2652724 |
| [13] |
Neely M. Stochastic network optimization with application to communication and queueing systems[M]. California, USA: Morgan & Claypool, 2010: 1.
|


