随着第5代移动通信系统(5G)时代到来^[1]，新型业务形态的出现使得业务需求呈爆炸式的增长. 5G热点高容量场景下通过小基站密集部署以提升资源复用率，从而有效承载超高数据流量并提升用户体验速率^[2-3].热点高容量场景下的资源匹配亦成为当前的研究热点.Chang等^[4]提出一种基于双眼抑制的非对称立体视频编码算法，通过自适应地调整视频业务的发送速率，以适应恶劣的信道状况.该类研究以业务为适配主体，以牺牲业务服务质量实现与紧缺资源的基本匹配，因而无法真正满足用户的业务需求. Tseng等^[5]提出一种面向5G超密集场景的资源分配算法，通过引入端到端技术以最大化系统容量.该类研究以网络为适配主体，未从用户业务需求出发，仅是单纯地优化网络性能，很有可能造成网络资源的浪费与不均衡分配.Zhang等^[6]提出一种5G多宿主场景下考虑信道动态性的能量有效的资源匹配算法，从而以最小的功耗统计地保障每个用户的业务速率需求. Zhao等^[7]面向具有多个内容提供商的小蜂窝场景，借助Stackelberg博弈建立分层优化模型，从而激励小基站提供相应资源给内容提供商.该类研究尽管通过网络优化以匹配业务需求，但是并未考虑业务需求的动态变化，故而无法有效适用于真实场景.

针对当前研究的不足，综合考虑了网络异构特征和业务动态变化特征，在热点高容量场景下，通过对业务动态性的预测，实时更新博弈的定价因子，以实现动态变化环境下网络资源与业务需求的最佳匹配.

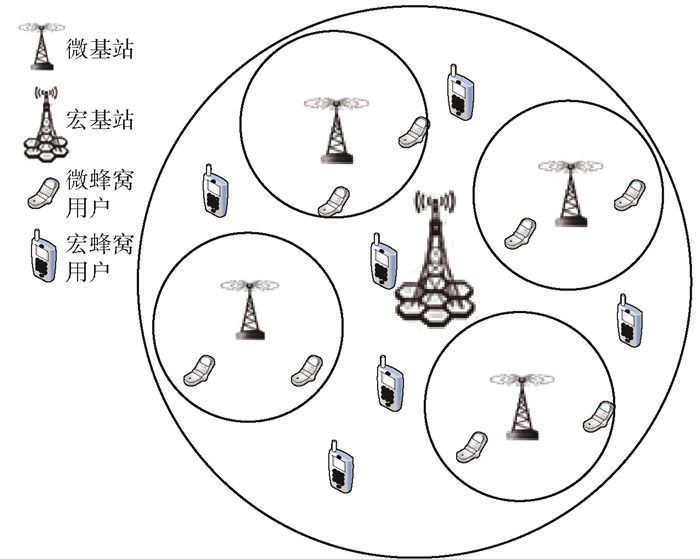
1 网络场景与系统假设

如图 1所示的热点高容量网络场景中，宏基站和微基站为用户提供服务.宏蜂窝用户和微蜂窝用户随机分布在热点高容量场景中.设微基站集合为Z={Z₁, Z₂, …, Z_S}，微基站Z_s∈Z；微基站Z_s覆盖范围内的微蜂窝用户集合为U_s={U₁, U₂, …, U_I}，微蜂窝用户U_i∈U_s；宏基站直接服务的宏蜂窝用户集合为M={M₁, M₂, …, M_J}，宏蜂窝用户M_j∈M.

考虑下行链路的功率分配，微基站和宏蜂窝用户共同竞争宏基站的功率资源，各微基站的微蜂窝用户共同竞争该微基站功率资源.由于参与者并不了解别人行动策略，微基站、宏蜂窝用户和微蜂窝用户存在着非合作竞争关系，可以视作非合作博弈问题^[8].故将双层异构网络的联合优化问题构建为双层博弈模型，并且做以下合理假设：①限定在单个宏基站覆盖的网络场景；②假设各小区的用户个数和用户位置保持不变；③假设每个用户业务都是可变速率业务；④每次功率博弈都对功率指标分配完毕，且满足下层功率总和等于上层博弈功率值的约束.

2 双层动态博弈模型

本文模型为两级博弈系统^[7].上层博弈是宏蜂窝用户与微基站之间关于宏基站功率资源分配的博弈，下层博弈是各微基站覆盖范围内的微蜂窝用户之间关于微基站功率资源分配的博弈.为得到最优功率资源分配方案，微基站以信道容量为效益函数，宏蜂窝用户、微蜂窝用户以用户满意度为效益函数.

2.1 上层博弈

1) 微基站功率博弈

宏基站用Z₀表示，共有S个微基站和J个宏蜂窝用户，微基站Z_s内共有I个微蜂窝用户.设每个用户各占一个带宽相等、互不干扰的信道.则Z_s的传输容量R_s为

$ {R_s} = \sum\limits_{i = 1}^I {\left[ {\frac{{{B_s}}}{I}\log \left( {1 + \gamma _s^ + \left( {{U_i}} \right)} \right)} \right]} $

(1)

$ \gamma _s^ + \left( {{U_i}} \right) = \frac{{{p_{{Z_s}}}}}{I}{\left( {\frac{\theta }{{4{\rm{ \mathsf{ π} }}{d_s}}}} \right)^2}\frac{{{g_{{t_s}}}{g_{{r_s}}}}}{{{n_{{o_s}}}}} $

(2)

其中：B_s为Z_s总带宽，p_Zs为分配给Z_s的发射功率，θ为载波波长，d_s为Z_s与所有小区用户平均距离，g_ts为Z_s发射天线增益，g_rs为Z_s内平均用户接收天线增益，n_os为Z_s内平均用户接收噪声功率，γ_s⁺(U_i)为U_i接收信噪比预估值.设∀Z_s∈Z的效益优化模型为

$ \begin{array}{l} \mathop {\max }\limits_{\forall {p_{{Z_s}}}} \left\{ {{\mathit{\Theta }_{{Z_s}}}\left( {{p_{{Z_s}}}} \right) = {R_s} - {c_{{Z_s}}}{p_{{Z_s}}}} \right\}\\ {\rm{s}}.\;{\rm{t}}.\left\{ \begin{array}{l} 0 \le {p_{{Z_s}}} \le p_{{Z_s}}^{\max }\\ \sum\limits_{s = 1}^S {{p_{{Z_s}}}} + \sum\limits_{j = 1}^J {{p_{{M_j}}}} = {p_0} \end{array} \right. \end{array} $

(3)

其中：Θ_Zs(p_Zs)表示Z_s的优化目标，c_Zs为Z_s的定价因子，c_Zsp_Zs为博弈惩罚项，p_Mj为分配给M_j的发射功率，$p_{{{z}_{s}}}^{\max }$为Z_s的最大分配功率，以确保小区边界成立，p₀为Z₀可分配的总功率指标.

2) 宏蜂窝用户功率博弈

M_j的接收信噪比函数为

$ \gamma \left( {{M_j}} \right) = {p_{{M_j}}}{\left( {\frac{\theta }{{4{\rm{ \mathsf{ π} }}{d_{{M_j}}}}}} \right)^2}\frac{{{g_t}\left( {{M_j}} \right){g_r}\left( {{M_j}} \right)}}{{{n_o}\left( {{M_j}} \right)}} $

(4)

其中：d_Mj为Z₀到M_j距离，g_t(M_j)和g_r(M_j)分别为Z₀与M_j的天线增益，n_o(M_j)为M_j接收噪声功率.选择Sigmoid型函数构建M_j的效益函数Φ(γ(M_j))，其为γ(M_j)的递增函数且满足：Φ(0)=0和Φ(∞)=1.故M_j的效益函数和惩罚函数分别定义为

$ \mathit{\Phi }\left( {\gamma \left( {{M_j}} \right)} \right) = \frac{1}{{1 + \exp \left[ { - {a_{{M_j}}}\left( {\gamma \left( {{M_j}} \right) - {b_{{M_j}}}} \right)} \right]}} $

(5)

$ \lambda \left( {{p_{{M_j}}}} \right) = {c_{{M_j}}}{p_{{M_j}}} $

(6)

其中：a_Mj为陡峭度系数，b_Mj为中心系数，c_Mj为M_j的定价因子.设∀M_j∈M的效益优化模型为

$ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\forall {p_{{M_j}}}} \left\{ {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{{M_j}}}\left( {{p_{{M_j}}}} \right) = \mathit{\Phi }\left( {\gamma \left( {{M_j}} \right)} \right) - \lambda \left( {{p_{{M_j}}}} \right)} \right\}}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\left\{ \begin{array}{l} 0 \le {p_{{M_j}}} \le p_{{M_j}}^{\max }\\ \sum\limits_{s = 1}^S {{p_{{Z_s}}}} + \sum\limits_{j = 1}^J {{p_{{M_j}}}} = {p_0} \end{array} \right.} \end{array} $

(7)

其中：Θ_Mj(p_Mj)表示M_j的优化目标，$p_{{M_j}}^{\max }$为M_j的最大分配功率. M_j对服务质量更敏感，故a_Mj取较大值.

2.2 下层博弈

U_i的接收信噪比函数为

$ \gamma _s^ * \left( {{U_i}} \right) = \frac{{{p_{{U_i}}}{{\left( {\frac{\theta }{{4{\rm{ \mathsf{ π} }}{d_{{U_i}}}}}} \right)}^2}{g_{{t_s}}}{g_r}\left( {{U_i}} \right)}}{{{n_o}\left( {{U_i}} \right)}} $

(8)

其中：γ_s^*(U_i)为U_i接收信噪比实际值，p_Ui为Z_s分配给U_i的实际功率，d_Ui为Z_s到U_i距离，g_r(U_i)为U_i的接收天线增益，n_o(U_i)为U_i接收噪声功率.故U_i的效益函数和惩罚函数分别为

$ \mathit{\Phi }\left( {\gamma _s^ * \left( {{U_i}} \right)} \right) = \frac{1}{{1 + \exp \left[ { - {a_{{U_i}}}\left( {\gamma _s^ * \left( {{U_i}} \right) - {b_{{U_i}}}} \right)} \right]}} $

(9)

$ {\lambda _s}\left( {{p_{{U_i}}}} \right) = {c_{{U_i}}}{p_{{U_i}}} $

(10)

其中：a_Ui为陡峭度系数，反应U_i对服务质量的敏感程度，故a_Ui取较小值，b_Ui为中心系数，c_Ui为U_i的定价因子.故设∀U_i∈U_s, ∀s的效益优化模型为

$ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\forall {p_{{U_i}}}} \left\{ {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{{U_i}}}\left( {{p_{{U_i}}}} \right) = \mathit{\Phi }\left( {\gamma _s^ * \left( {{U_i}} \right)} \right) - {\lambda _s}\left( {{p_{{U_i}}}} \right)} \right\}}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\left\{ \begin{array}{l} 0 \le {p_{{U_i}}} \le p_{{U_i}}^{\max }\\ \sum\limits_{i = 1}^I {{p_{{U_i}}}} = p_{{Z_s}}^ * \end{array} \right.} \end{array} $

(11)

其中：Θ_Ui(p_Ui)表示U_i的优化目标，$p_{{U_i}}^{\max }$为U_i的最大分配功率，p_Zs^*为上层博弈得到的Z_s的最佳分配功率.

2.3 基于业务动态预测的定价因子更新

对业务动态性进行建模与预测，以此为基础周期地运行功率资源匹配算法，实现算法有效性和实现代价的最佳折中.这里，业务动态性包括2个方面：业务到达动态性和业务速率动态性.基于业务动态性预测，可得到微基站、宏蜂窝用户和微蜂窝用户的业务需求量.显然，业务需求量越大应相应分配更多的网络资源；反之亦然，从而实现网络资源与业务需求的匹配.给定上层博弈优化目标，即$\sum\limits_{s = 1}^S {{\mathit{\Theta }_{{z_s}}}} \left( {{p_{{z_s}}}} \right) + \sum\limits_{j = 1}^J {{\mathit{\Theta }_{{M_j}}}} \left( {{p_{{M_j}}}} \right)$，合理调整定价因子c_Zs, ∀Z_s和c_Mj, ∀M_j，即可实现p₀约束下功率资源按需分配；给定下层博弈优化目标，即$\sum\limits_{i = 1}^I {{\mathit{\Theta }_{{U_i}}}} \left( {{p_{{U_i}}}} \right)$，合理调整定价因子c_Ui, ∀U_i∈U_s, ∀s，即可实现p_Zs^*约束下功率资源按需分配.由定价因子的物理内涵可知，增大某个定价因子，将减少相应的资源分配量；反之亦然.

2.3.1 业务空闲模型

对于任一用户U(宏蜂窝用户或微蜂窝用户)，设其业务空闲时间服从参数t_▽的指数分布，相应的概率分布函数为f_▽(t).需要说明的是，不同用户具有不同的t_▽参数，应在实际系统中周期性地统计更新.

在每个周期初始时刻执行一次功率资源匹配算法，故当U在周期初始时刻处于业务接入状态，则整个周期不论其始终处于接入状态还是中途变为空闲状态，均设其状态标识F=1，即U参与资源分配.当U在周期初始时刻处于业务空闲状态，若1－f_▽(T+T₀)≥1－ε₁，则U将以很大概率保持空闲状态，故设F=0，即U不参与资源分配；反之则U可能中途变为接入状态，故设F=1，即U参与资源分配.其中，ε₁为概率保障参数1，1－ε₁为相应的置信度，T为周期时长，T₀为U处于空闲状态的已持续时间.

2.3.2 业务速率模型

假定U接入可变速率业务，故设其业务速率服从均值为ζ，方差为σ²的高斯分布，相应的概率分布函数为f_V(v).需要说明的是，不同用户具有不同的ζ和σ²参数，应在实际系统中周期性地统计更新.

求解优化模型$\mathop {\min }\limits_{\forall \mathit{\Lambda }} \{ \mathit{\Lambda }\} $, s.t.f_V(Λ)≥1－ε₂，得到最优解Λ^*，即U的业务速率以置信度1－ε₂(ε₂为概率保障参数2)不大于Λ^*.显然，只要满足Λ^*，则认为网络资源与业务需求实现匹配(匹配概率为1－ε₂).

2.3.3 定价因子动态更新策略

初始化各类参数：t_▽、ζ、σ²、∀c_Zs、∀c_Mj和∀c_Ut.在后续每个周期，执行如下定价因子更新策略.

1) 统计更新各用户的t_▽参数，根据业务空闲模型，预测各用户的业务状态：若F=0，则相应用户不进入用户集合，且不参与资源分配；若F=1，则相应用户进入用户集合且参与资源分配.

2) 统计更新各用户的ζ和σ²参数，根据业务速率模型，预测进入用户集合各用户的业务速率需求Λ^*，即微蜂窝用户速率Λ^*_{s, Ui}和宏蜂窝用户速率Λ_Mj^*.

3) 更新上层博弈的定价因子：∀Z_s∈Z执行更新公式

$ \begin{array}{*{20}{c}} {c_{{Z_s}}^{\mho + 1} = } \\ {c_{{Z_s}}^\mho - \Delta \left[ {\sum\limits_{\forall i} {\mathit{\Lambda }_{s,{U_i}}^*} - \sum\limits_{\forall s} {\sum\limits_{\forall i} {\mathit{\Lambda }_{s,{U_i}}^*} } + \frac{{\sum\limits_{\forall j} {\mathit{\Lambda }_{{M_j}}^*} }}{{S + J}}} \right]} \end{array} $

其中：c_Zs$^{{\mho} +1}$和c_Zs$^{\mho}$分别为Z_s的下一周期和当前周期的定价因子，Δ为更新尺度系数，$\sum\limits_{\forall i}{\mathit{\Lambda }_{s, {{U}_{i}}}^{*}}$为Z_s的业务速率需求. ∀M_j∈M执行更新公式

$ c_{{M_j}}^{\mho + 1} = c_{{M_j}}^\mho - \Delta \left[ {\mathit{\Lambda }_{{M_j}}^* - \sum\limits_{\forall s} {\sum\limits_{\forall i} {\mathit{\Lambda }_{s,{U_i}}^*} } + \frac{{\sum\limits_{\forall j} {\mathit{\Lambda }_{{M_j}}^*} }}{{S + J}}} \right] $

其中：c_Mj$^{{\mho} +1}$和c_Mj$^{\mho}$分别为M_j的下一周期和当前周期的定价因子.

4) 更新下层博弈的定价因子：∀U_i∈U_s, ∀s执行更新公式$c_{{{U}_{i}}}^{{\mho} +1}=c_{{{U}_{i}}}^{\mho }-\Delta \left[ \mathit{\Lambda }_{{{U}_{i}}}^{*}-\sum\limits_{\forall i}{\mathit{\Lambda }_{{{U}_{i}}}^{*}}/I \right], c_{{{U}_{i}}}^{{\mho} +1}$和c_Ui$^{{\mho} +1}$分别为U_i的下一周期和当前周期的定价因子.

2.4 算法求解

上层博弈是M_j和Z_s关于总功率指标p₀的分配问题，利用拉格朗日乘子法，可得上层梯度下降求解算法；下层博弈是Z_s内各用户U_i关于Z_s功率指标p_Zs^*的分配问题，利用拉格朗日乘子法，可得下层梯度下降求解算法.上述流程限于篇幅，不再赘述.在此基础上，本文算法的总体流程简述如下：

1) 网络环境初始化和各类参数初始化；

2) 每个周期初始时刻，执行定价因子更新策略；

3) 给定定价因子，执行上层梯度下降求解算法；

4) 给定定价因子，执行下层梯度下降求解算法；

5) 输出功率最优解p^*_Mj, ∀j和p^*_Ui, ∀i, ∀s.

由不动点定理可得^[8]，上、下层博弈均存在纳什均衡解，且分别由上、下层梯度下降求解算法可得.

3 仿真结果与讨论

在1 000 m×1 000 m的矩形区域，以宏基站为中心，覆盖范围内随机部署S个微基站和J个宏蜂窝用户，每个微基站的覆盖范围内随机部署I个微蜂窝用户.宏基站覆盖半径设为500 m，微基站覆盖半径均值为100 m.而且，保证微基站之间距离至少100 m以上.所有微基站和所有宏蜂窝用户的信道相互正交，带宽分别为20 MHz和5 MHz，所有噪声功率谱密度统一设为－174 dBm，功率指标p₀在区间[500 W, 1 000 W]随机确定.初始化各类参数：∀c_Zs=1、∀c_Mj=2、∀c_Ui=2、a_Mj=3、b_Mj=1、a_Ui=1、b_Ui=1、∀g_t(M_j)=5、∀g_r(M_j)=1、∀g_ts=1、∀g_r(U_i)=1、ε₁=ε₂=0.05、T=10 min.

为实现业务动态性，业务空闲时间参数t_▽取值服从均匀分布，均值为120 s；各用户业务速率模型参数ζ和σ取值服从均匀分布，均值分别为256 kbit/s和16 kbit/s.为验证本文算法(OA, our algorithm)性能，选择平均功率分配算法(APAA, average power allocation algorithm)、随机功率分配算法(RPAA, random power allocation algorithm)和静态功率分配算法(SPAA, static power allocation algorithm)^[9]用于仿真比较. APAA算法通过平均分配方式实现功率指标的两层分配；RPAA算法通过随机分配方式实现功率指标的两层分配；SPAA算法是基于当前业务速率需求以用户服务质量为优化目标的功率最优分配算法.采用Matlab加以实现，所有仿真结果均是20次仿真的平均值.

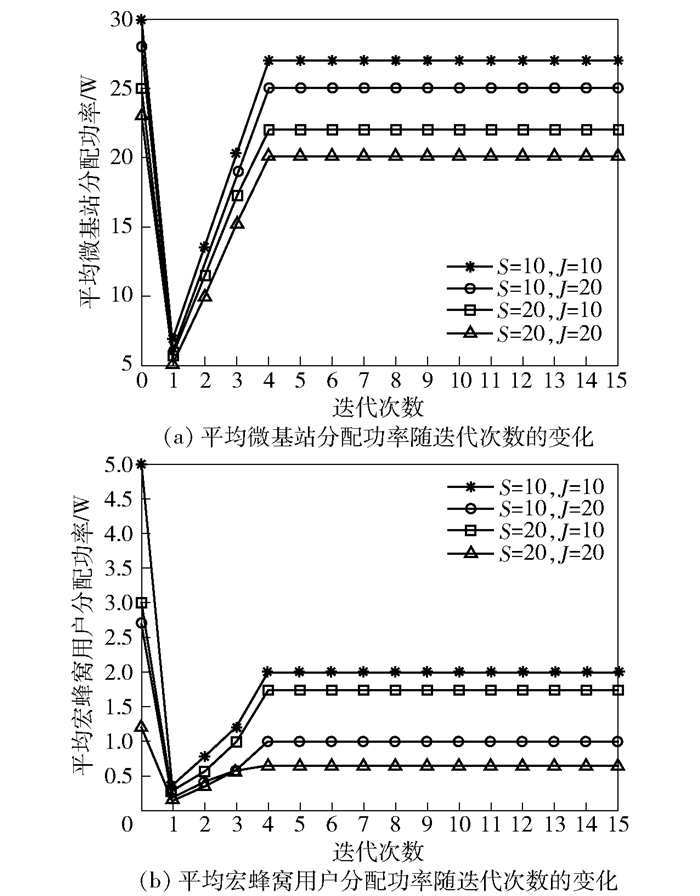
上层博弈算法的理论复杂度为O(S+J)，是微基站与宏蜂窝用户总个数的线性函数.在实际系统中，引入信令交互，分布式实现该算法，故该算法复杂度变为常量(O(1)). 图 2给出了基于本文上层博弈算法的平均微基站分配功率和平均宏蜂窝用户分配功率随迭代次数的变化曲线.可以看出，随着微基站与宏蜂窝用户个数的增加，平均微基站分配功率和平均宏蜂窝用户分配功率均呈降低趋势；随着迭代次数的增加，上层博弈算法能够快速收敛到最优解，在第4次迭代即实现收敛.

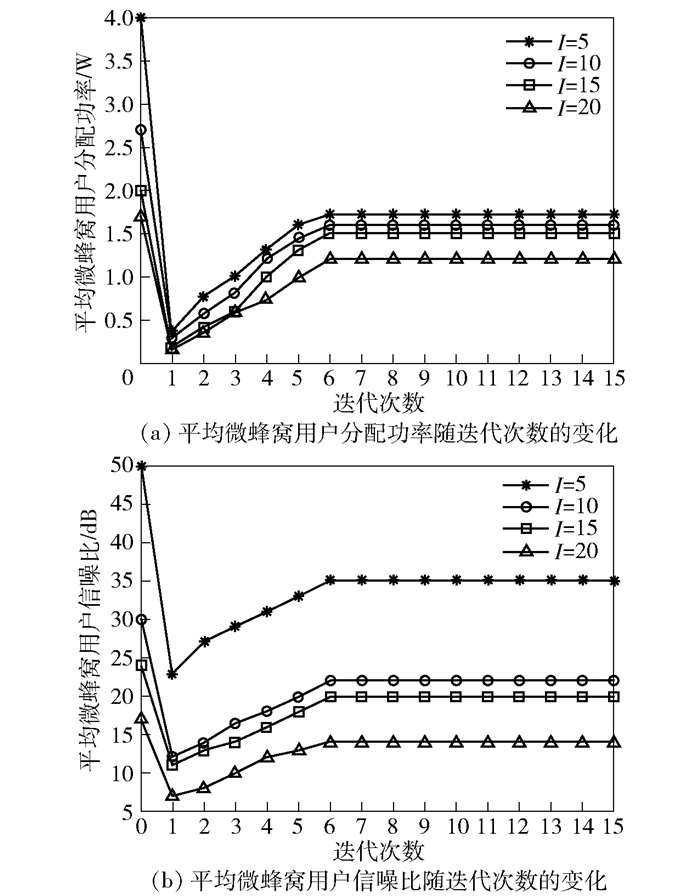
下层博弈算法的理论复杂度为O(I)，是微蜂窝用户个数的线性函数.在实际系统中，引入信令交互，分布式实现该算法，故该算法复杂度变为常量(O(1)).给定S=15、J=15，图 3给出了基于下层博弈算法的平均微蜂窝用户分配功率和平均微蜂窝用户信噪比随迭代次数的变化曲线.可以看出，随着单个小区微蜂窝用户个数的增加，平均微蜂窝用户分配功率和平均微蜂窝用户信噪比均呈降低趋势；随着迭代次数的增加，下层博弈算法能够快速收敛到最优解，在第6次迭代即可实现收敛.

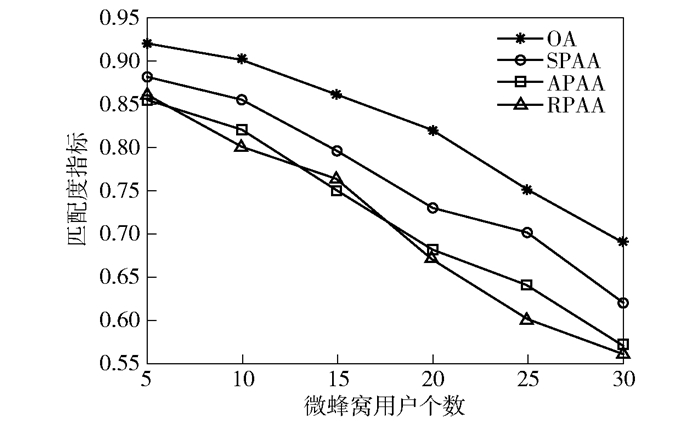
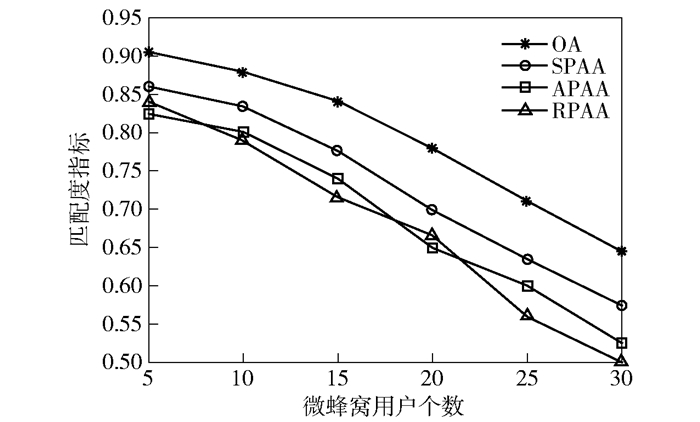
给定S=15，图 4和图 5分别给出了在不同宏蜂窝用户个数情况下基于本文算法、SPAA、APAA、PPAA 4类算法的匹配度指标随微蜂窝用户个数的变化曲线.匹配度指标定义为业务需求得到满足的用户个数与用户总数(包括宏蜂窝用户和微蜂窝用户)的比值，以衡量4类算法在业务动态变化环境下的资源配置性能.特别地，提供给某个用户的下行传输容量始终大于该用户的业务速率需求，则视为该用户的业务需求得到满足.由图 4和图 5可知，随着单个小区微蜂窝用户个数I的增加，即用户总数快速增加，平均用户分配功率降低，使得下行传输容量相应降低，故4类算法的匹配度指标均呈快速下降趋势；同样地，随着宏蜂窝用户个数J的增加，即用户总数缓慢增加，故4类算法的匹配度指标均呈缓慢下降趋势.由于APAA和RPAA未从用户的业务速率需求出发进行功率分配，故2类算法分配的网络资源与业务需求的匹配性能最差；SPAA仅从当前业务需求出发进行功率分配，而未考虑业务动态变化，故该算法分配的网络资源与业务需求的匹配性能处于中间位置；本文算法采用基于业务动态性预测的定价因子更新策略，使得功率资源按需分配，故本文算法在各种情况下均具有最优的匹配性能.当然，由于预测误差的存在，基于本文算法的匹配度指标亦无法达到1.

4 结束语

提出了一种面向热点高容量场景的功率资源匹配算法.建立双层动态博弈模型，针对不同博弈层参与者设计不同的效益模型，并通过对网络中业务动态性的预测实时调整定价因子，以更准确地反映网络环境的变化.仿真结果证明了本文算法的有效性.