2. 东南大学 移动通信国家重点实验室, 南京 210096;
3. 国家无线电监测中心, 北京 100037
针对短波无线电测向场地选址困难的问题,提出了一种基于改进多信号分类(MUSIC)算法的短波非规则天线阵列测向系统.该算法可使短波无线电测向系统部署在地势平坦地区,还可以部署在山区、丘陵等复杂地形,有效解决了短波无线电测向系统的选址问题.在对该算法进行理论建模和计算机仿真验证的基础上,开发了短波非规则阵列测向原型系统,并在实际环境中进行了大量现场测试.测试结果表明,改进MUSIC算法具备了在非规则阵列条件下进行来波信号方位测定的能力,相应的非规则天线阵列测向系统能够在复杂地形条件下实现测向功能.
2. National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China;
3. State Radio Monitoring Center, Beijing 100037, China
Traditional high frequency (HF) finding system needs a large and plain area for antenna array, so it is difficult to find a suitable place for practical HF direction finding systems. To address this issue, an improved mutiple signal classification (MUSIC) algorithm is proposed for HF direction finding system with non-regular antenna array. This algorithm makes it possible to deploy HF direction finding system not only in plain area but also in the conditions of complex terrain, which makes it much easier to find a place to deploy HF direction finding system. On the basis of theoretical modeling and computer simulation, a prototype system of HF irregular array direction finding was developed and tested in the real environment. The experiment results showed that the improved MUSIC algorithm was available for direction finding in the condition of non-regular antenna array, and the corresponding HF direction finding systems can work well with complex terrain conditions.
短波无线电测向是短波无线电监测的一项重要内容[1-2].中国各地短波监测站建设较早,近些年,由于社会发展,多地无线电监测站周边的地形地貌较早期设计规划阶段已经出现了较大变化,并且监测站周边人员活动更加密集,恶化了短波测向系统周边的电磁环境.由于周边地形地貌和电磁环境的恶化,各地短波测向系统均出现测向性能恶化的现象,部分旧有监测站测向系统甚至已经无法达到预期设计指标,新短波测向系统建设已经迫在眉睫.
虽然新短波测向系统建设十分迫切,但新系统的选址却十分困难.目前, 短波测向系统普遍采用了短波天线阵的方式来实现.短波天线阵对场地有严格的地形地貌要求,如地势平坦、面积较大.同时,短波天线阵周边必须具备优良的电磁环境,以保证测向系统各项性能达标.由于短波测向天线阵对场地的地形、地貌和周边电磁环境有着严格要求,测向场地选址对新短波测向系统建设的各个环节都形成了巨大的挑战,带来了难以克服的困难,阻碍了短波测向系统的建设和部署.
传统无线电测向技术,大多采用基于幅度或者相位的方法判断来波方位,其精度较低、容易受干扰信号影响[3-5].多信号分类(MUSIC,mutiple signal classification)算法的提出是无线电测向技术的一大进步[6],它不仅提出了一种具备“超分辨”能力的测向算法,更为重要的是开辟了一类以线性空间为基础的现代无线电测向理论,各种基于MUSIC算法思想的改进算法层出不穷[7-8].近些年,以压缩感知为代表的稀疏信号处理技术被应用到无线电测向的研究中,并获得了有意义的理论结果[9-12].虽然无线电测向相关研究已经较多,但大多数是以传统规则天线阵列结构为基础,针对复杂地形条件下非规则阵列结构,特别是具有高程差地形条件下的三维天线阵列结构的测向技术研究较少.
笔者提出了一种基于改进MUSIC算法的非规则天线阵列测向系统.该算法使短波无线电测向系统不但可以部署在地势平坦地区,还可以部署在山区、丘陵等复杂地形条件下,极大拓展了测向场地可供选择的范围,有效解决了短波无线电测向系统的选址问题.在理论分析和仿真验证的基础,给出原型系统的建设,以及仿真和实验结果.
1 短波非规则天线阵列测向系统由于非规则天线阵列结构根据实际地形部署,所形成的阵列结构具有三维空间结构.与传统阵列结构不同的是,由于传统测向阵列采用平面结构,所以使用二维坐标即可描述阵列结构;而非规则阵列由于具有三维结构,所以除了平面坐标外,还需要高程差参数才可以描述阵列结构.
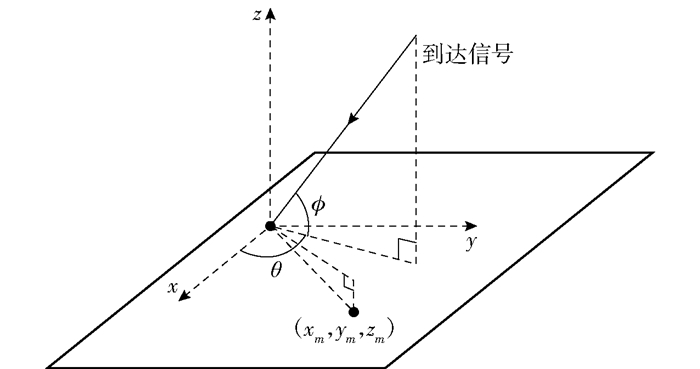
基于平面阵列的传统测向系统中,导向向量主要由方位角来决定.采用三维天线阵列结构后,导向向量由方位角和俯仰角共同决定.如图 1所示,图中xy平面为地平面,z轴表示高程差维度,θ表示来波信号的方位角,ϕ表示来波信号的俯仰角.
|
图 1 来波信号示意图 |
假设非规则天线阵列测向系统中共有M根天线,第m根天线坐标为(xm, ym, zm).以坐标原点为相位参考点,非规则天线阵列的导向向量可以表示为
| $ \mathit{\boldsymbol{a}}\left( {\theta ,\phi } \right) = {\left[ {{a_1}\left( {\theta ,\phi } \right), \cdots ,{a_M}\left( {\theta ,\phi } \right)} \right]^{\rm{T}}} $ | (1) |
其中:向量a(θ, ϕ)的第m个元素可以表示为
| $ {a_m}\left( {\theta ,\phi } \right) = {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {{x_m}\cos \phi \cos \theta + {y_m}\cos \phi \sin \theta + {z_m}\sin \phi } \right)}} $ | (2) |
其中λ为来波信号的波长.利用am(θ, ϕ),第m根天线在第n个时刻接收到的信号可以表示为
| $ {r_m}\left[ n \right] = s\left[ n \right]{a_m}\left( {\theta ,\phi } \right) + {w_m}\left[ n \right] $ | (3) |
其中:s[n]和wm[n]分别为接收机收到的发送信号和噪声信号,其平均功率可以表示为
| $ E\left( {{{\left| {s\left[ n \right]} \right|}^2}} \right) = \sigma _s^2,E\left( {{{\left| {{w_m}\left[ n \right]} \right|}^2}} \right) = \sigma _w^2 $ | (4) |
因此,接收信号的信噪比可以定义为
| $ \gamma = \frac{{\sigma _s^2}}{{\sigma _w^2}} $ | (5) |
将各个天线上的接收信号写成向量形式为
| $ \mathit{\boldsymbol{r}}\left[ n \right] = \mathit{\boldsymbol{a}}\left( {\theta ,\phi } \right)s\left[ n \right] + \mathit{\boldsymbol{w}}\left[ n \right] $ | (6) |
其中
| $ \mathit{\boldsymbol{r}}[n] = {\left( {{r_1}[n], \cdots ,{r_M}[n]} \right)^{\rm{T}}} $ | (7) |
| $ \mathit{\boldsymbol{w}}[n] = {\left( {{w_1}[n], \cdots ,{w_M}[n]} \right)^{\rm{T}}} $ | (8) |
应当注意的是,由于大多广播电台带宽较窄,所以式(6)考虑了窄带信号的情况,也就是说,不同天线之间的接收信号相位差仅取决于天线的导向向量.
2 改进MUSIC算法改进MUSIC算法的目标就是在给定如式(6)的接收信号后,估计出来波信号的俯仰角和方位角.本节中,首先对算法步骤进行介绍,然后对所提出的改进MUSIC算法进行分析.
2.1 算法步骤改进MUSIC算法流程包括4个主要步骤:获取空域协方差矩阵、获取噪声空间基向量、构造搜索导向向量和角度搜索.
1) 获取空域协方差矩阵
空域协方差矩阵定义为不同天线接收信号的统计平均值.由于统计结果一般无法直接获取,所以一般采用时域样本平均的方法来估计空域协方差矩阵.在进行样本平均之前,需要对接收信号进行功率归一化,即
| $ {{\tilde r}_m}[n] = \frac{{{r_m}[n]}}{{\sqrt {\sum\limits_{n = 0}^{N - 1} {{{\left| {{r_m}[n]} \right|}^2}} } }} $ | (9) |
其中N为时域采样点的个数.功率归一化后,空域协方差矩阵的估计值可以表示为
| $ \mathit{\boldsymbol{\hat R}} = \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {\mathit{\boldsymbol{\tilde r}}} [n]{{\mathit{\boldsymbol{\tilde r}}}^{\rm{H}}}[n] $ | (10) |
其中
2) 获取噪声空间基向量
空域协方差矩阵
| $ \mathit{\boldsymbol{\hat R}} = \left( {{\mathit{\boldsymbol{U}}_D},{\mathit{\boldsymbol{V}}_{M - D}}} \right)\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_D}}&{}\\ {}&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{M - D}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_D^{\rm{H}}}\\ {\mathit{\boldsymbol{V}}_{M - D}^{\rm{H}}} \end{array}} \right) $ | (11) |
其中:ΣD为D×D维的特征值矩阵;D为信号空间维度,对于只有一个来波信号源的情况,可以取D=1;UD为M×D维次酉矩阵,代表信号子空间基向量;VM-D为M×(M-D)维次酉矩阵,并且与UD正交,其M-D个基向量构成了所求的噪声子空间基向量.
3) 构造搜索导向向量
假设用于角度搜索的方位角和俯仰角分别为θ0、ϕ0,那么按照式(1)构造出的非规则天线阵列条件下的搜索导向向量可以表示为
| $ \mathit{\boldsymbol{a}}\left( {{\theta _0},{\phi _0}} \right) = {\left[ {{a_1}\left( {{\theta _0},{\phi _0}} \right), \cdots ,{a_M}\left( {{\theta _0},{\phi _0}} \right)} \right]^{\rm{T}}} $ | (12) |
4) 角度搜索
当到达信号的方位角为θ0,俯仰角为ϕ0时,对应的非规则转动向量a(θ0, ϕ0)处于信号空间中.利用信号空间与噪声空间的正交关系,可以得到
| $ \mathit{\boldsymbol{V}}_{M - D}^{\rm{H}}\mathit{\boldsymbol{a}}\left( {{\theta _0},{\phi _0}} \right) = {\bf{0}} $ | (13) |
通过在给定的角度范围内进行搜索,来波信号的方位角和俯仰角可以通过最大化如下代价函数获得:
| $ \left\{ {\hat \theta ,\hat \phi } \right\} = \mathop {\arg \max }\limits_{\left\{ {{\theta _0},{\phi _0}} \right\}} \frac{1}{{{{\left\| {\mathit{\boldsymbol{V}}_{M - D}^{\rm{H}}\mathit{\boldsymbol{a}}\left( {{\theta _0},{\phi _0}} \right)} \right\|}_2}}} $ | (14) |
下面将对改进MUSIC算法进行更加深入的分析,以观察其与传统规则阵列条件下MUSIC算法的区别.
1) 功率归一化
传统规则阵列测向系统中,接收信号可以直接用于空域协方差矩阵估计,一般不需要功率归一化操作.这是因为传统测向系统一般部署在地形平坦的开阔场地,由于场地条件较好,所以各个天线接收到的信号强度基本一致.
与传统规则平面列结构不同的是,由于非规则天线阵列采取了地形匹配的部署方式,地形条件可能会产生对部分信号的遮挡,导致各个接收天线上的信号强度相差较大.因此,需要先对接收信号进行功率归一化操作,以避免不同天线上接收信号强度的差别对空域协方差矩阵估计带来的影响.
2) 无特定结构导向向量
传统规则阵列中,由于天线阵列结构具有的规律性,所以构造出的导向向量也会带有一定的结构特征.比如,均匀直线阵列条件下,导向向量各元素间具有等比例关系,当存在多个信号源时,导向矩阵可以构成Vandermonde矩阵[13];在均匀平面阵列条件下,导向向量具有嵌套结构[14].合理利用导向向量中的结构特征,不但可以简化算法性能分析,还可以运算复杂度的降低.
非规则天线阵列条件下,由于天线阵列不具有规律性,所以构造出来的导向向量也不具有特定结构.从算法设计角度来看,由于导向向量没有特定结构,所以对算法的性能分析变得十分困难;另一方面,由于导向向量没有特定结构可供利用,所以只能采用二维角度域搜索的方法来求解式(12).
通过上面的分析可以看出,虽然非规则阵列结构可以有效解决短波无线电测向系统的选址问题,但在算法层面,它也带来一些新的挑战.但是,随着计算机仿真技术的进步和高性计算单元的出现,非规则天线阵列的性能可以借助大量仿真实验得到充分验证,复杂的二维搜索算法也可以利用高性能计算单元弥补.从这个角度来说,算法层面引入的挑战并不会影响非规则天线阵列测向系统在实际中的部署和应用.
3) 高程差对测向性能的影响
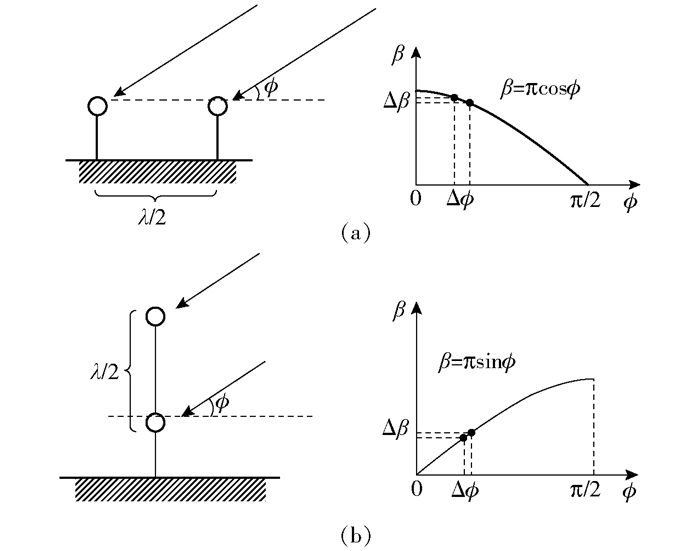
改进MUSIC算法与传统规则阵列的另外一个重要之处在于引入了高程差,也就是式(2)中的zmsinϕ一项.高程差的引入有利于改善俯仰角的测向精度.为了详细说明这一问题,对比图 2(a)和图 2(b). 图 2(a)给出的是典型的平面阵列的情况,2根接收天线水平放置,接收信号相位差与俯仰角是余弦关系,即
| $ \beta = {\rm{ \mathsf{ π} cos}}\phi $ | (15) |
|
图 2 高程差对俯仰角测向性能的影响 |
当俯仰角较小时,余弦函数变化缓慢,微小的相位测量误差Δβ就会带来较大的俯仰角估计误差Δϕ.如果考虑如图 2(b)所示的情况,此时2根接收天线垂直放置,俯仰角与接收信号相位差的关系式变成正弦关系,即
| $ \beta = {\rm{ \mathsf{ π} sin}}\phi $ | (16) |
当俯仰角较小时,正弦函数变化较为迅速,微小的相位误差Δβ所带来的俯仰角估计误差Δϕ也较小.对比图 2(a)和图 2(b)可知,当天线阵列具有高程差时,可以有效改善小俯仰角情况下的俯仰角测向精度.由于实际中大部分短波信号都是以中、低俯仰角到达接收天线阵列,所以在天线阵列各天线单元间引入高程差,有利于改善俯仰角的测向精度,从而提升整体的测向性能.
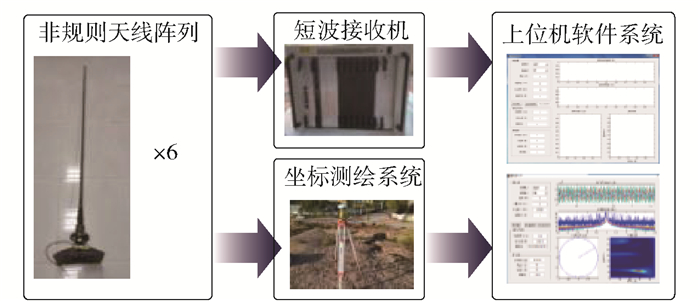
3 原型系统建设在理论研究和算法分析的基础上,为了对非规则天线阵列测向系统进行实验验证,搭建了短波非规则天线阵列测向原型系统,如图 3所示.该原型系统主要包括短波非规则天线阵列、短波接收机和上位机软件3部分.天线阵列接收到的信号送入接收机,接收机对信号采样后将采样结果发送给上位机软件,由上位机软件实现测向算法.
|
图 3 上位机软件图形界面 |
1) 短波非规则天线阵列
短波非规则天线阵列由6根高为1.8 m的短波接收天线组成,该接收天线为单极子结构,水平方向增益为4.5 dB;天线单元在三维空间的位置坐标由专用测量仪器根据实际地形条件下的阵列部署情况实地测量得到.
2) 短波接收机
短波接收机具有6个接收通道,每个接收通道可以覆盖3~30 MHz的短波信号范围,并且有最高128 kHz的信号采样频率.各通道相位误差小于1°,每通道接收机的灵敏度为105 dBm.该接收机具有低失真、常规和低噪声3种模式,对应于低、中、高3种增益模式,各个增益模式间相差10 dB.
考虑到器件老化对校准参数的影响,以及采用数字中频接收方案时,各个接收通道采用了异本振结构,因此接收机结构设计中引入了自校准信号源和开关矩阵.装备了自校准源和开关矩阵后,每次测向操作前都可以对各个接收通道进行1次实时校准,保证了测向结果的准确性,并克服了由于环境变化所带来的校准参数失效问题.
3) 上位机软件
上位机软件主要实现数据采集功能和信号处理功能,可以实现采样数据的自动读取、自动保存和信号处理操作,不但简化了测向操作流程,还可以实现历史数据回放.上位机软件以1个测向周期为基本时间单元周期性工作.每个测向周期内,上位机软首先根据图形界面输入参数形成命令帧,随后将命令帧发送到短波接收机.短波接收机提取命令帧中的参数并对接收通道做出相应配置后,启动信号采集.采集结束后短波接收机形成回复帧,并将回复帧发回给上位机软件.上位机软件从回复帧中提取出采集到的信号样本,并执行测向算法,最后将测向结果显示到图形界面.
4 实验结果为了对算法进行验证,并对短波非规则天线阵列测向原型系统进行系统性测试,在武夷山地区开展了现场测试与实验,如图 4所示.由于武夷山地区地形地貌以山地为主,地形条件较为复杂,所以非常适合非规则天线阵列的场地选址;另一方面,福建省无线电监测站的短波测向系统位于武夷山地区,在此处开展实验,便于将实验结果与现有测向系统进行对比.

|
图 4 实验现场 |
实验中采用了具有6天线单元的非规则阵列结构.考虑了2组天线阵列,天线阵列的三维空间坐标如表 1所示.第1组天线阵列中,天线单元的最大水平距离为33.1 m,最大高程差3.8 m;第2组天线阵列中,天线单元的最大水平距离为22.0 m,最大高程差达到2.2 m. 2组天线阵列的1号天线位置相同,均位于(0, 0, 0)点.
|
|
表 1 实验中使用的天线阵列坐标 |
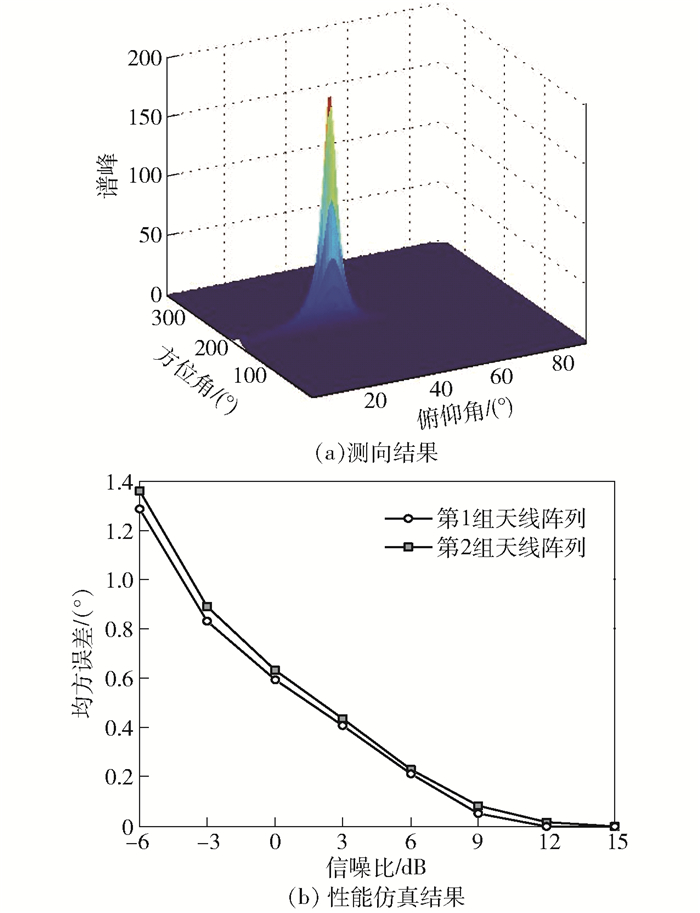
图 5中给出了2组天线阵列性能的仿真结果,仿真中考虑到了载波为10 MHz的信号. 图 5(a)中给出了2组天线阵列在入射信号俯仰角为30°,方位角为200°时的测向结果.可以看出,图中曲面峰值出现的位置对应来波信号的方位角和俯仰角. 图 5(b)中给出了2组天线阵列的性能仿真对比.从图中可以看出,第1组天线阵列的性能要优于第2组天线阵列,这是因为第1组天线阵列具有较大的孔径,因此其性能要比第2组天线阵列好.
|
图 5 2组天线阵列仿真结果 |
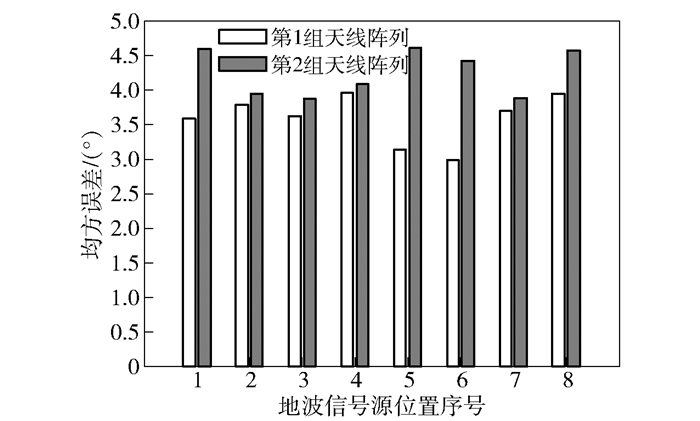
图 6给出了地波信号源实验的结果.地波测试中,在天线阵列周围选取了8个已知位置点,在已知位置点处发送频率3~30 MHz的短波信号.对于某个给定位置,假设来波信号真实方位角为θ,对不同频率来波信号的测向结果为θn,那么测向的均方误差可以表示为
| $ \Delta \theta = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{\left| {{\theta _n} - \theta } \right|}^2}} } $ | (17) |
|
图 6 地波实验结果 |
对比图 6中的测试结果可以看到,由于第1组天线阵列孔径较大,所以测向性能略优于第2组天线阵列,这与从图 5仿真结果中观察到的现象是一致的.
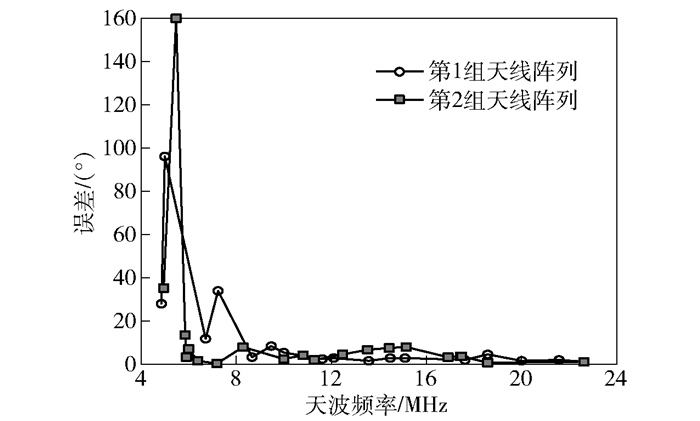
图 7中给出了天波测向的实验结果.横轴表示所测量的天波信号频率,纵轴表示原型系统测量得到的方位角与武夷山监测站现有测向系统测量结果之间的误差.从图中可以看到,当信号频率处于中高频段时,2组天线阵列与现有监测站测向结果十分吻合,而当频率较低时,2组天线阵列与现有监测站测向结果相差较大.这是由于2组天线阵列的最大孔径较小,因而对低频信号测向结果较差,对中、高频信号测向结果较好.
|
图 7 天波实验结果 |
针对短波测向系统的选址问题,提出了一种基于改进MUSIC算法的短波非规则天线阵列测向系统.该系统不但可以部署在地势平坦地区,还可以部署山地、丘陵等复杂地形条件下,极大拓展了短波测向系统的选择范围,有效解决了短波测向系的选址问题.在详细介绍了改进MUSIC算法和原型系统建设的基础上,还对实验结果进行了详细的对比分析.实验结果表明,短波非规则天线阵列测向系统研究达到了预期的研究目标,实验中所使用的非规则天线阵列测向系统具备了基本的测向能力,适合应用在地形复杂的山地、丘陵条件下部署短波无线电测向系统.
| [1] |
胡中豫编著. 现代短波通信[M]. 北京: 国防工业出版社, 2005.
|
| [2] |
国家无线电管理委员会办公室. 无线电管理业务手册[M]. 北京, 1993.
|
| [3] |
王鼎, 吴瑛, 张莉. 无线电测向与定位理论及方法[M]. 北京: 国防工业出版社, 2016.
|
| [4] |
刘宝平, 叶李超. 干涉仪测向中二维拟合算法研究[J]. 通信对抗, 2014, 33(3): 31-34. Liu Baoping, Ye Lichao. 2-D fitting algorithm research of DF method of correlation interferometer[J]. Communication Countermeasures, 2014, 33(3): 31-34. |
| [5] |
张清清.基于相关干涉的测向技术研究[D].成都: 电子科技大学, 2013. http://d.wanfangdata.com.cn/Thesis/D772513
|
| [6] |
Schmidt R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 |
| [7] |
Dai J, Bao X, Hu N, et al. A recursive RARE algorithm for DOA estimation with unknown mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2014(13): 1593-1596. |
| [8] |
Elbir A M. Direction finding in the presence of direction-dependent mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2017(16): 1541-1544. |
| [9] |
Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022. DOI:10.1109/TSP.2005.850882 |
| [10] |
Gerstoft P, Xenaki A, Mecklenbrauker C F, et al. Multiple snapshot compressive beamforming[C]//2015 49th Asilomar Conference on Signals, Systems and Computers. New York: IEEE Press, 2015: 1774-1778.
|
| [11] |
Wang Xianpeng, Meng Dandan, Huang Mengxing, et al. Reweighted regularized sparse recovery for DOA estimation with unknown mutual coupling[J]. IEEE Communications Letters, 2019, 23(2): 290-293. DOI:10.1109/LCOMM.2018.2884457 |
| [12] |
Fortunati S, Grasso R, Gini F, et al. Single snapshot DOA estimation using compressed sensing[C]//2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New York: IEEE Press, 2014: 2297-2301.
|
| [13] |
张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004.
|
| [14] |
Mathews C P, Zoltowski M D. Eigenstructure techniques for 2-D angle estimation with uniform circular arrays[J]. IEEE Transactions on Signal Processing, 1994, 42(9): 2395-2407. DOI:10.1109/78.317861 |


