2. 南宁学院 信息工程学院, 南宁 530200
为了优化能量收集无线网络传输性能,延长网络中能量受限型节点的生命周期,提出了一种基于解码转发策略的机会协作中继系统动态时间分配策略.在满足系统最低传输速率的约束下,推导出中断概率与时间分配系数之间的关系表达式;通过减小系统中断概率来优化时间分配系数,得出系统吞吐量和能量效率的表达式;设计了一种基于次优迭代的时间分配算法,实现问题的求解.仿真实验结果表明,在非理想信道状况下,所提出的策略有较高的系统吞吐量和能量效率,可优化无线网络的传输性能,提高可靠运行度.
2. School of Information Engineering, Nanning University, Nanning 530200, China
A dynamic time allocation strategy for opportunistic cooperative relay system was proposed to optimize the transmission and extend the life cycle of energy-constrained nodes in energy harvesting wireless network. The relationship between outage probability and time distribution coefficient was derived under the constraint of satisfying the minimum transmission rate of the system. By reducing the system outage probability, the time allocation coefficient was optimized and the expression of the system throughput and energy efficiency was deduced. A suboptimal iteration time allocation algorithm was designed to solve the problem. The simulation results show that the proposed strategy is of higher system throughput and energy efficiency under the non-ideal channel condition, which will optimize the transmission performance and improve the reliability of the system.
能量收集无线网络[1]是一种节点自带能量收集装置的网络,能将环境中的能量收集并转化成可用的电能供给无线设备完成网络通信任务[2-3].无线携能传输(SWIPT, simultaneous wireless information and power transfer)技术利用射频信号,可同时携带能量与信息,为无线网络中的能量受限型节点延长生命周期提供了解决方案[4].但是,随着传输距离的增加,传播路径损耗会变得越来越大,导致能量传输的效率随之逐渐降低.该问题亟待解决.
协作中继技术具有成本低、拓展网络覆盖范围等作用,是未来无线网络关键技术之一,在无线网络中得到广泛应用[5-7].将协作中继技术与无线携能传输技术结合起来,可优化能量收集无线网络的传输性能,增强系统的可靠运行度[8-13].笔者给出了一种基于解码转发策略的机会协作中继系统动态时间分配策略,通过构建时间分配系数与中断概率的数学模型,减小系统中断概率,优化无线网络的传输性能,并给出仿真结果与分析.
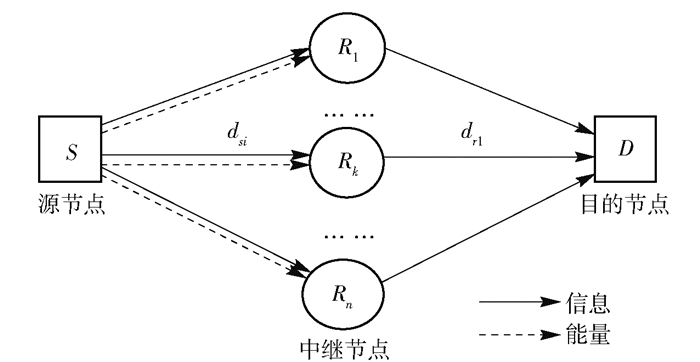
1 系统模型一个机会协作中继系统的模型如图 1所示,其包含一个源节点S、n个中继节点Ri(i=1, 2, …, n)和一个目的节点D.假设系统中各信道都是瑞利衰减信道,由于存在信道衰落,导致S和D之间无法直接传输,需要利用机会中继协作才能完成信号的传输.为此,各节点都配有一条天线,工作模式是半双工模式.一开始,每个中继节点Ri本身无任何能量,需从S发射的信号中获取能量并存储在自身电池中,然后利用收集到的能量完成信息转发任务.
|
图 1 机会协作中继系统模型 |
假设电池容量无限大,系统中整个传输块的周期为t.传输分为2个阶段.第1阶段为源节点S给所有中继节点广播发射信号阶段,传输时间为θt(0<θ<1).第2阶段的传输时间为(1-θ)t,工作任务是从能正确解码的中继节点中选取一个最佳中继(假设是Rk),然后利用收集到的能量解码转发信息到目的节点D.考虑到选择最佳中继节点所需的时间相对于整个传输周期很小,忽略不计.
在第1阶段,中继节点Ri(i=1, 2, …, n)采用功率分流策略将接收到的源节点S信号xs分为两部分,其中ρriLPS部分的信号用于能量收集,(1-ρri)PS用于信息接收,PS为源节点S的传输功率. LPS为S的发射功率,ρri(0 < ρri < 1)为Ri的功率划分因子. Ri接收的信号yri可表示为
| $ {y_{{r_i}}} = \sqrt {\left( {1 - {\rho _{{r_j}}}} \right){L_{{\rm{PS}}}}{h_{s{r_i}}}} {x_s} + {n_{{r_i}}} $ | (1) |
其中:hsri=gsridsri-αsri/2为S与Ri之间的链路信道因子,gsri为S到Ri之间的瑞利衰减系数,dsri为S到Ri的距离,αsri为路径损耗指数,nri为Ri产生的噪声且服从分布nri~CN(0, σ2sri),其中σ2sri为噪声方差.中继节点Ri收集到的能量可表示为
| $ {E_{{r_i}}} = \eta {\rho _{{r_i}}}{L_{{\rm{PS}}}}{\left| {{h_{s{r_i}}}} \right|^2}\theta t $ | (2) |
其中η(0 < η < 1)为能量转换效率系数.
由香农公式可知,中继节点Ri可实现的端到端传输速率可表示为
| $ \begin{array}{*{20}{c}} {{T_{rd}} = \left( {1 - \theta } \right)1{\rm{b}}\left( {1 + \frac{{{L_{{\rm{PS}}}}{{\left| {{h_{s{r_i}}}} \right|}^2}}}{{\sigma _{s{r_i}}^2}}} \right) = }\\ {\theta 1{\rm{b}}\left( {1 + \left( {1 - {\rho _{{r_i}}}} \right){L_{{\rm{PS,}}{\mathit{r}_\mathit{i}}}}{{\left| {{h_{s{r_i}}}} \right|}^2}} \right)} \end{array} $ | (3) |
其中LPS, ri=LPS/σ2sri.
在第2阶段,需要从能够正确解码信息的中继集合U中选择一个最佳中继Rk完成转发任务,而机会中继选择策略是从集合U中选取到目的节点信道系数最大的中继作为最佳中继[14],即
| $ {R_k} = \mathop {\arg \max {{\left\{ {\left| {{h_{{r_i}d}}} \right|} \right.}^2}}\limits_{i \in U} $ | (4) |
其中hrid为中继Ri到目的节点D的信道因子.
Rk使用收集到的能量将信息转发给目的节点D.假定D的信号为xd,则Rk的传输功率为
| $ {T_{{r_k}}} = \frac{{{E_{{r_k}}}}}{{\left( {1 - \theta } \right)t}} = \frac{\theta }{{\left( {1 - \theta } \right)}}\eta {\rho _k}{L_{{\rm{PS}}}}{\left| {{h_{sk}}} \right|^2} $ | (5) |
目的节点D接收信号yd可表示为
| $ {y_d} = \sqrt {{T_{{r_k}}}{L_{\mathit{kd}}}{x_d}} + {n_d} $ | (6) |
其中:hkd=gkddkd-αkd/2为中继节点Rk与目的节点D之间的链路信道因子,gkd为Rk到D之间的瑞利衰减系数,且服从分布gkd~CN(0, 1),dkd为Rk与D之间的距离,αkd为路径损耗指数,nd为Rk到D的加性高斯白噪声且服从分布nd~CN(0, σkd2).
因此,目的节点D可实现的端到端传输速率为
| $ \begin{array}{*{20}{c}} {{T_{rd}} = \left( {1 - \theta } \right)1{\rm{b}}\left( {1 + \frac{{{T_{{r_k}}}{{\left| {{h_{\mathit{kd}}}} \right|}^2}}}{{\sigma _{kd}^2}}} \right) = }\\ {\left( {1 - \theta } \right)1{\rm{b}}\left( {1 + {T_{{r_k}d}}{{\left| {{h_{\mathit{kd}}}} \right|}^2}} \right)} \end{array} $ | (7) |
其中Trkd=Trk/σkd2.为方便后面的公式表达,定义βkd=LPS/σkd2,βsri=LPS/σ2sri.
2 动态时间分配策略本节将基于无线携能传输的机会协作中继系统模型进行研究分析,推导出系统中断概率和时间分配系数的表达式,通过减小中断概率进一步优化时间分配系数,进而得出系统吞吐量和能量效率的表达式.
2.1 中断概率与时间分配系数的关系推导中断是指因节点即时速率低于目标速率时发生的事件.系统中断时需考虑2种情况:一是集合|U|=n,时在n个中继正确解码信息后从中选取一个最佳中继转发,若最佳中继中断则系统发生中断;二是当集合U=Ø,即没有中继转发信息到目的节点,则n=0.那么可得系统中断概率Pop表达式为
| $ \Pr \left\{ {U = \emptyset } \right\} = \prod\limits_{i = 1}^N {\Pr \left\{ {{{\left| {{h_{s{r_i}}}} \right|}^2} < \frac{{{\tau _k}}}{{{\beta _{s{r_i}}}}}} \right\}} $ | (8) |
其中:U=Ø表示没有中继能够参与转发信息的中断概率,此时n=0.
n个中继可成功解码信息的概率表示为
| $ \begin{array}{*{20}{c}} {\Pr \left\{ {\left| U \right| = n} \right\} = \prod\limits_{i \in U}^n {\Pr \left\{ {{\gamma _i} \ge \gamma _k^*} \right\}\prod\limits_{j \in \bar U}^{N - n} {\Pr \left\{ {{\gamma _i} < \gamma _k^*} \right\} = } } }\\ {\prod\limits_{i \in U}^n {\left[ {1 - \Pr \left\{ {{\gamma _i} < \gamma _k^*} \right\}} \right]\prod\limits_{j \in \bar U}^{N - n} {\Pr \left\{ {{\gamma _i} < \gamma _k^*} \right\} = } } }\\ {\prod\limits_{i \in U}^n {\left[ {1 - \Pr \left\{ {{{\left| {{h_{s{r_i}}}} \right|}^2} < \frac{{{\tau _k}}}{{{\beta _{s{r_i}}}}}} \right\}} \right]\prod\limits_{j \in \bar U}^{N - n} {\Pr \left\{ {{{\left| {{h_{s{r_j}}}} \right|}^2} < \frac{{{\tau _k}}}{{{\beta _{s{r_j}}}}}} \right\}} } } \end{array} $ | (9) |
其中:
U=Ø时,每个中继的即时信噪比都会小于目标信噪比,所以此时的中断概率表示为
| $ \begin{array}{*{20}{c}} {\Pr \left\{ {\mathit{\boldsymbol{U}} = \emptyset } \right\} = \prod\limits_{i = 1}^N {\Pr \left\{ {{\gamma _i} < \gamma _k^*} \right\}} = }\\ {\prod\limits_{i = 1}^N {\Pr \left\{ {{{\left| {{h_{si}}} \right|}^2} < \frac{{{\tau _k}}}{{{\beta _{si}}}}} \right\}} } \end{array} $ | (10) |
在式(8)中,Pr{γd < γd*}表示中继节点到目的节点链路的中断概率,用Pout表示如下:
| $ {P_{{\rm{out}}}} = \Pr \left\{ {{\gamma _d} < \gamma _d^*} \right\} = 1 - P\left[ D \right] $ | (11) |
其中P[D]为目的端的成功概率.
对于整个系统而言,为了确保中继Rk收集到足够的能量用于传输信息,即S-Rk链路速率Lk达到最低速率要求可以正确解码信息,假定Lk=Lk*,即θlb(1+γk)=lb(1+γk*),可得γk=(1+γk*)1/θ-1.联合式(7)得γk=(1-ρk)Trk|hsk|2 =(1+γk*)1/θ-1,所以可得功率划分因子
| $ {T_{{r_k}}} = \max \left\{ {0,\eta \left( {{L_{{\rm{PS}}}}{{\left| {{h_{sk}}} \right|}^2} - {\tau _k}\sigma _{sk}^2} \right)\theta /\left( {1 - \theta } \right)} \right\} $ |
源节点和中继之间进行无线携能传输,要求出中继节点Rk到目的节点D的中断概率Pout,可先求出该链路的成功概率:
| $ P\left[ D \right] = \Pr \left\{ {\left( {1 - \theta } \right)1{\rm{b}}\left( {1 + {T_{{r_k}d}}{{\left| {{h_{kd}}} \right|}^2}} \right) \ge R_d^*,{T_{{r_k}d}} > 0} \right\} $ | (12) |
其中:P[D]可通过简单变化进一步表示如下:
| $ \begin{array}{*{20}{c}} {P[D] = }\\ {\int_{\frac{{{\tau _k}}}{{{\beta _{sk}}}}}^\infty {{f_{{{\left| {{h_{sk}}} \right|}^2}}}\left( z \right){T_{{r_k}}}\left\{ {{{\left| {{h_{kd}}} \right|}^2} > \frac{{{\tau _d}\left( {1 - \theta } \right)}}{{\eta \theta \left( {{\beta _{skd}}z - \frac{{{\tau _k}\sigma _{sk}^2}}{{\sigma _{kd}^2}}} \right)}}} \right\}{\rm{d}}z = } }\\ {d_{sr}^{{a_{ri}}}\int_{\frac{{{\tau _k}}}{{{\beta _{sk}}}}}^\infty {{{\rm{e}}^{\frac{{\frac{{d_{kd}^{{a_{kd}}}\left( {1 - \theta } \right){\tau _d}}}{{{\tau _d}\left( {1 - \theta } \right)}}}}{{\eta \theta \left( {{\beta _{skd}}z - \frac{{{\tau _k}\sigma _{sk}^2}}{{\sigma _{kd}^2}}} \right)}}}}{{\rm{e}}^{ - d_{sk}^{{a_{rk}}}z}}{\rm{d}}z} = }\\ {\sqrt[{{{\rm{e}}^{\frac{{ - d_{sk}^{{a_{r{k_\tau }}}}k}}{{{\beta _{sk}}}}}}}]{{\frac{{4d_{sk}^{{a_{rk}}}d_{kd}^{{a_{rd}}}\left( {1 - \theta } \right){\tau _d}}}{{\eta \theta {\beta _{skd}}}}}}{K_1}\left( {\sqrt {\frac{{4d_{sk}^{{a_{rk}}}d_{kd}^{{a_{rd}}}\left( {1 - \theta } \right){\tau _d}}}{{\eta \theta {\beta _{skd}}}}} } \right)} \end{array} $ | (13) |
其中:
又因为节点的信道系数|h|2的概率密度函数表示为f|h|2(x)=be-bx,b为信道系数|h|2的均值;|h|2的累积分布函数F|h|2(y)=Pr{|h|2 < y}=1-ey.将概率密度函数和累积分布函数代入并结合概率积分知识,式(13)的中继成功概率表达式可表示为
| $ \begin{array}{*{20}{c}} {P[{D_1}] = }\\ {\int_{\frac{{{\tau _k}}}{{{\beta _{sk}}}}}^\infty {{f_{{{\left| {{h_{sk}}} \right|}^2}}}\left( z \right){T_{{r_k}}}\left\{ {{{\left| {{h_{kd}}} \right|}^2} > \frac{{{\tau _1}\left( {1 - \theta } \right)}}{{\eta \theta \left( {{\beta _{sk1}}z - \frac{{{\tau _k}\sigma _{sk}^2}}{{\sigma _{k1}^2}}} \right)}}} \right\}{\rm{d}}z = } }\\ {d_{sr}^{{a_r}}\int_{\frac{{{\tau _k}}}{{{\beta _{sk}}}}}^\infty {{{\rm{e}}^{\frac{{ - d_{k1}^{{a_{k1}}}\left( {1 - \theta } \right){\tau _1}}}{{\eta \theta \left( {{\beta _{sk1}}z - \frac{{{\tau _k}\sigma _{sk}^2}}{{\sigma _{k1}^2}}} \right)}}}}{{\rm{e}}^{ - d_{sk}^{{a_{rk}}}z}}{\rm{d}}z} = }\\ {\sqrt[{{{\rm{e}}^{\frac{{ - d_{sk}^{{a_{r{k_\tau }}}}k}}{{{\beta _{sk}}}}}}}]{{\frac{{4d_{sk}^{{a_{rk}}}d_{k1}^{{a_{k1}}}\left( {1 - \theta } \right){\tau _1}}}{{\eta \theta {\beta _{sk1}}}}}}{K_1}\left( {\sqrt {\frac{{4d_{sk}^{{a_{rk}}}d_{k1}^{{a_{r1}}}\left( {1 - \theta } \right){\tau _1}}}{{\eta \theta {\beta _{sk1}}}}} } \right)} \end{array} $ | (14) |
得到中继成功概率表达式后,由式(11)可得到中继Rk到D链路中断概率Pout的闭式表达式为
| $ \begin{array}{*{20}{c}} {{P_{{\rm{out}}}} = 1 - d_{sr}^{{a_{rk}}}\int_{\frac{{{\tau _k}}}{{{\beta _{sk}}}}}^\infty {{{\rm{e}}^{\frac{{\frac{{d_{kd}^{{a_{kd}}}\left( {1 - \theta } \right){\tau _d}}}{{{\tau _d}\left( {1 - \theta } \right)}}}}{{\eta \theta \left( {{\beta _{skd}}z - \frac{{{\tau _k}\sigma _{sk}^2}}{{\sigma _{kd}^2}}} \right)}}}}{{\rm{e}}^{ - d_{sk}^{{a_{rk}}}z}}{\rm{d}}z} = }\\ {1 - {{\rm{e}}^{\frac{{ - d_{sk}^{{a_{rk}}}{\tau _k}}}{{{\beta _{sk}}}}}}\omega {K_1}\left( \omega \right)} \end{array} $ | (15) |
其中:dskark为最佳中继Rk与源节点之间的距离,αrk为路径损耗指数,
根据前述分析可知,U=Ø时第i个中继发生中断的条件为
| $ \begin{array}{*{20}{c}} {\Pr \left\{ {\mathit{\boldsymbol{U}} = \emptyset } \right\} = \prod\limits_{i = 1}^N {\Pr \left\{ {{{\left| {{h_{s{r_i}}}} \right|}^2} < \frac{{{\tau _k}}}{{{\beta _{s{r_i}}}}}} \right\}} = }\\ {{{\left( {\int_0^{\frac{{{\tau _k}}}{{{\beta _{sk}}}}} {d_{kd}^{{a_{kd}}}{{\rm{e}}^{ - xd_{sk}^{{a_{rk}}}}}dx} } \right)}^N} = {{\left[ {1 - {{\rm{e}}^{\frac{{d_{sk}^{{a_{r{k_\tau }}}}k}}{{{\beta _{sk}}}}}}} \right]}^N}} \end{array} $ | (16) |
同理,也可以得到Pr{|U|=n}的表达式为
| $ \Pr \left\{ {\left| \mathit{\boldsymbol{U}} \right| = n} \right\} = {\left[ {1 - {{\rm{e}}^{\frac{{ - d_{sk}^{{a_{r{k_\tau }}}}k}}{{{\beta _{sk}}}}}}} \right]^{N - n}}{\left[ {{{\rm{e}}^{\frac{{ - d_{sk}^{{a_{r{k_\tau }}}}k}}{{{\beta _{sk}}}}}}} \right]^n} $ | (17) |
为了便于表示,令
| $ {P_{{\rm{op}}}} = {\psi ^N} + \sum\limits_n^N {\left( {\begin{array}{*{20}{c}} N\\ n \end{array}} \right)} {\left( {1 - \mathit{\Psi }} \right)^n}{\mathit{\Psi }^{N - n}}{P_{{\rm{out}}}} $ | (18) |
由式(18),在一定目标速率V下,可得到与中断概率有关的源节点S到目的节点D的吞吐量表示,即
| $ C = \left( {1 - {P_{{\rm{op}}}}} \right)V\left( {1 - \theta } \right) $ | (19) |
而系统的能量效率则表示为
| $ \frac{C}{{{P_{{\rm{total}}}}}}\frac{{\left( {1 - {P_{{\rm{op}}}}} \right)V\left( {1 - \theta } \right)}}{{{L_{{\rm{PS}}}}T}} $ | (20) |
根据式(18),以最小化系统中断概率为目标优化时间分配,则目标优化模型为
| $ \begin{array}{*{20}{l}} {\min {P_{{\rm{op}}}}}\\ {{\rm{s}}{\rm{. t}}{\rm{. 0 < }}\theta < 1,0 < {\rho _k} < 1} \end{array} $ | (21) |
式(21)表示最小化中断概率的目标函数,约束条件为时间分配系数θ以及功率划分因子ρk.根据2.1节的分析可知,中断概率其实只受时间分配系数θ的约束,所以可知目标函数是关于θ的凸函数,故存在一个最优值θ使得中断概率最小[15].但是,由于目标函数中包含有贝塞尔函数,使得直接求解θ的最优值十分困难.为此,利用一种低复杂度的次优迭代的时间分配算法去求解目标函数,以降低求解的难度.优化后的时间分配算法步骤描述如下.
算法1 时间分配算法
输入:瞬时信道状态CSI,噪声方差σr2、σkd2和源节点总功率值TPS,能量转换效率系数η,目标速率Lk*、Lkd*,路径损耗指数αri、αkd,源节点S到中继节点Rk的距离dsri,中继Rk到目的节点D的距离dkd.
输出:可最小化中断概率的时间分配系数θ*.
初始化:a0=0,a1=1,迭代次数i = 1,误差Δ,步长ζ
1 While| a0-a1|>Δ do
2 θ=(a0+a1)/2
3 If (Pop(θ) < Pop(θ+ζ)) Then
4 a0=θ
5 end If
6 If (Pop(θ)>Pop(θ+ζ)) Then
7 a1=θ
8 end If
9 end While
10 θ*=(a0+a1)/2
11 Return θ*
3 仿真实验与性能分析仿真实验的目的是:一是验证本文动态时间分配策略(简称本文传输策略)的收敛性;二是将本文传输策略与文献[13]提出的功率分流中继传输策略(简称PSR传输策略)在不同变量情况下的吞吐量和能量效率进行对比分析,说明本文传输策略在优化传输性能方面的有效性和优势.
仿真参数设置如下:中继节点数N=3,源节点S的传输功率PS=3 dBm,源节点S到中继Ri的距离dsri=1.2 m,中继节点Rk到目的节点D的距离dkd=2.5 m;能量转换效率系数η=0.7,源节点到中继节点Ri的路径损耗指数αri=1.2,中继节点Rk到目的节点D的路径损耗指数αkd=2.7;噪声方差σkd2=σsk2=-29 dBm.
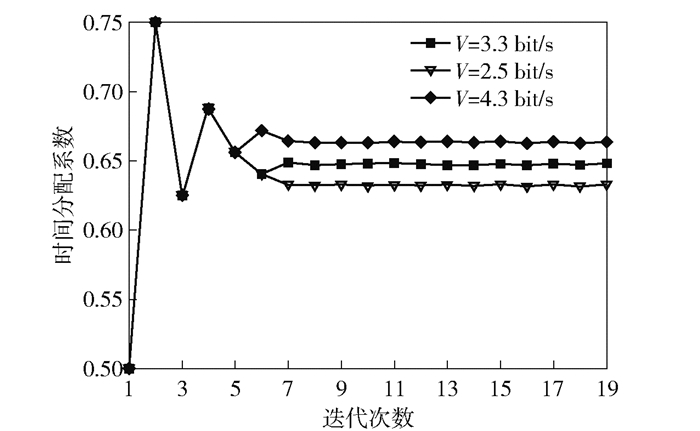
图 2给出了本文传输策略对应的时间分配算法收敛性的实验结果.从实验结果看,在不同的目标速率下,本文传输策略中的时间分配系数会在有限次迭代后逐步收敛于某个值.
|
图 2 迭代次数与时间分配系数的关系 |
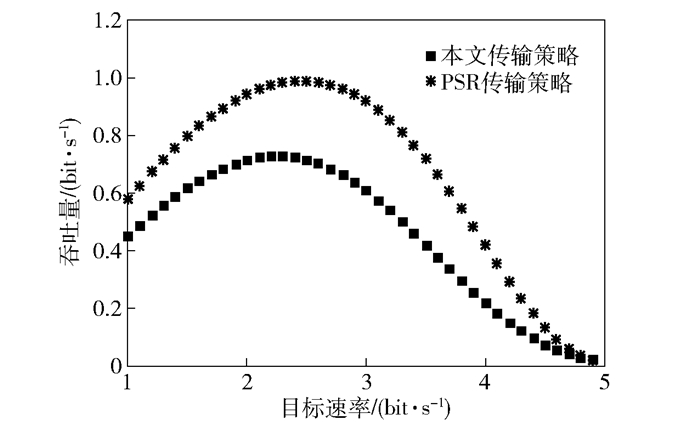
图 3为应用PSR传输策略和本文传输策略后吞吐量与目标速率的关系.从实验结果中可以看出,当目标速率增加时,2种策略的吞吐量变化曲线的走向是先升后降.这是由于中继用来转发信息的能量来源于能量收集,而在传输功率固定时,速率越大意味着分配用于信息解码的传输功率需增大,那么会导致用于收集能量的功率减少,能量不够则会导致中断事件发生机率增大,由此可知速率和能量存在均衡.当中继节点目标速率较小时,PSR传输策略与本文传输策略差距不是很大.但是当中继的目标速率增大到2.5~4 bit·s-1时,本文传输策略与PSR传输策略的差距明显增大,这是因为当目标速率增大时时间分配会影响到资源的利用率,而资源的有效利用对系统的中断性能也会产生影响,进而影响到系统的吞吐量.随着速率继续增大,2种策略的差距逐渐减小.总体上看,由于本文传输策略采用了动态时间分配的策略,所以其吞吐量优于时间分配没有变化的PSR传输策略.
|
图 3 不同传输策略时吞吐量与目标速率的关系 |
图 4给出了从源节点S到目的节点D传输线路上不同路径损失情况下,2种传输策略在传输功率与中断概率的关系上的实验对比结果.实验中假设V=2.5 bit·s-1.从图中可看到,当传输线路上的路径损耗指数αri、αkd相差较小时,2种传输策略在性能上差距不明显.当路径损耗指数增大时,在同一传输功率下,本文传输策略的中断概率明显小于PSR传输策略.这是由于路径损失会影响到链路信道增益,当路径损失增大时信道增益会减小,进而对中断性能产生影响.由于本文传输策略增大了传输功率,弥补了因路径损失降低的性能,而且合理的时间分配也会使功率资源得以有效利用,进而提高了系统性能.这说明了当路径损失增大时本文传输策略的性能优于PSR传输策略.

|
图 4 不同路径损失下传输功率和中断概率的关系 |
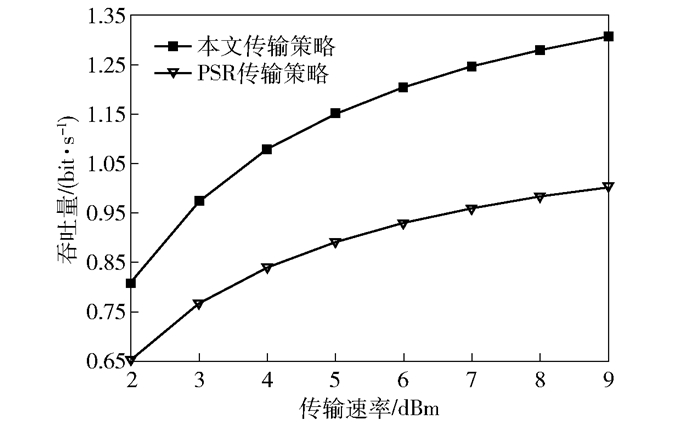
图 5给出了V=2.5 bit·s-1时2种传输策略的吞吐量和传输功率的关系.从实验对比结果中可以看到,2种传输策略的吞吐量都随着传输功率的增大而增大,这是因为传输功率增大时,收集的能量会随之增大,而能量越多意味着可以传输更多的信息,进而提高了系统的吞吐量.在给定的时间分配优化策略下,当传输功率较小时,本文传输策略的吞吐量与PSR传输策略相差不大;当传输功率增大时,本文传输策略的吞吐量明显大于PSR传输策略.其中的原因在于:传输功率增大会减少中断概率,而合理的时间分配会进一步提升中断性能,使得系统吞吐量得到提高.
|
图 5 不同传输策略时吞吐量与传输功率的关系 |
图 6给出了2种传输策略的能量效率与传输功率的关系,其中的能量效率是指吞吐量与消耗的传输功率的比值.从图 6的实验结果可以看到,在传输功率较低时本文传输策略可实现比较高的能量效率,这是因为本文传输策略采取的合理时间分配提高了系统的吞吐量.从图中还可以看到,随着传输功率的增大,2种传输策略的能量效率呈下降趋势,且两者的能量效率差别逐步缩小.这是因为在一定的目标速率下,传输功率的增大会对中断概率产生影响,使得吞吐量会随传输功率的增加而缓慢上升,且增加的幅度比传输功率低.而能量效率是吞吐量与传输功率的比值,会随着功率增大而逐步降低.因此,在低功率情况下,所提传输策略的性能优势会更加明显.

|
图 6 不同传输策略时能量效率与传输功率的关系 |
基于解码转发策略的无线携能传输机会协作中继系统,深入分析了动态调整时间分配对系统传输性能的影响,构建了系统信道容量模型,提出了一种最小化中断概率的中继动态时间分配策略.首先对系统目的节点的中断概率进行分析,推导出系统中断概率与时间分配系数之间关系的表达式;然后以最小化中断概率为目标,基于时间分配系数的约束,构建中断概率优化模型,得出中断概率是关于时间分配系数的凸函数,运用低复杂度的迭代算法来求解问题.仿真结果表明,与现有的PSR传输策略相比,提出的传输策略能够有效降低系统中断概率,提高系统吞吐量和能量效率,优化了系统的传输性能,保障了系统的可靠运行.
| [1] |
Ulukus S, Yener A, Erkip E, et al. Energy harvesting wireless communications:a review of recent advances[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 360-381. DOI:10.1109/JSAC.2015.2391531 |
| [2] |
Lu Xiao, Wang Ping, Niyato D, et al. Wireless charging technologies:fundamentals, standards, and network applications[J]. IEEE Communications Surveys and Tutorials, 2016, 18(2): 1413-1452. DOI:10.1109/COMST.2015.2499783 |
| [3] |
Krishore R A, Priya S. A review on low-grade thermal energy harvesting:materials, methods and devices[J]. Materials, 2018, 11(8): 1433. DOI:10.3390/ma11081433 |
| [4] |
Liu Liang, Zhang Rui, Chua K C. Wireless information and power transfer:a dynamic power splitting approach[J]. IEEE Transactions on Communications, 2013, 61(9): 3990-4001. DOI:10.1109/TCOMM.2013.071813.130105 |
| [5] |
Nasir A A, Zhou Xiangyun, Durrani S, et al. Relaying protocols for wireless energy harvesting and information processing[J]. IEEE Transactions on Wireless Communications, 2013, 12(7): 3622-3636. DOI:10.1109/TWC.2013.062413.122042 |
| [6] |
Orhan O, Erkip E. Energy harvesting two-hop communication networks[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(12): 2658-2670. DOI:10.1109/JSAC.2015.2481206 |
| [7] |
Chen Zhi, Dong Yunquan, Fan Pingyi, et al. Optimal throughput for two-way relaying:energy harvesting and energy cooperation[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(5): 1448-1462. DOI:10.1109/JSAC.2016.2551481 |
| [8] |
Ding Haiyang, Wang Xiaodong, da Costa D B, et al. Adaptive time-switching based energy harvesting relaying protocols[J]. IEEE Transactions on Communications, 2017, 65(7): 2821-2837. DOI:10.1109/TCOMM.2017.2693358 |
| [9] |
Zhong Shaohong, Huang Huajun, Li Renfa. Outage probability of power splitting SWIPT two-way relay networks in Nakagami-m fading[J]. EURASIP Journal on Wireless Communications and Networking, 2018(11): 1-8. |
| [10] |
Liu Yuan. Optimal power splitting for SWIPT-based MIMO DF relay systems[C]//2017 IEEE International Conference on Communications(ICC). New York: IEEE Press, 2017: 1-6.
|
| [11] |
Liu Yuan. Joint resource allocation in SWIPT-based multi-antenna decode-and-forward relay networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 9192-9200. DOI:10.1109/TVT.2017.2717018 |
| [12] |
姚媛媛, 李学华, 黄赛, 等. 基于携能通信的大规模无线协作网络中断性能分析[J]. 北京邮电大学学报, 2018, 41(6): 20-25. Yao Yuanyuan, Li Xuehua, Huang Sai, et al. Outage characterization of large-scale wireless cooperative networks based on SWIPT[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(6): 20-25. |
| [13] |
Liu Yuanwei, Ding Zhiguo, Elkashlan M, et al. Cooperative non-orthogonal multiple access with simultaneous wireless information and power transfer[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 938-953. DOI:10.1109/JSAC.2016.2549378 |
| [14] |
彭磊, 臧国珍, 高媛媛, 等. 机会中继协同通信系统在Nakagami-m衰落信道中的折中性能分析及系统优化[J]. 计算机应用研究, 2018, 36(12): 1-7. Peng Lei, Zang Guozhen, Gao Yuanyuan, et al. Tradeoff performance analysis and system optimization of opportunistic relay cooperative communication system under Nakagami-m fading channe[J]. Application Research of Computers, 2018, 36(12): 1-7. |
| [15] |
Komjáth P, Totik V. Problems and theorems in classical set theory[M]. New York: Springer, 2006.
|


