基于2.55 GHz市区微蜂窝多输入多输出信道实测数据,将机器学习中的最小二乘支持向量机(LS-SVM)算法应用于时变信道参数的建模中,建立了基于遗传算法(GA)优化的LS-SVM信道参数预测模型,对信道参数如时延扩展、接收端的水平角度扩展和垂直角度扩展的数据特征进行了学习,并实现了准确预测;同时通过与反向传播神经网络模型以及传统的LS-SVM模型进行比较,验证了算法的有效性.基于GA优化的LS-SVM模型能够在有限数据量下对信道参数的变化有着良好的适应性,可实现非线性时变信道参数的准确预测.
Based on 2.55 GHz urban microcellular multiple-input multiple-output (MIMO) channel measurement data, the least squares support vector machine (LS-SVM) method was applied on time-varying channel model. Specifically, a genetic algorithm (GA) based LS-SVM (GA+LS-SVM) model was established for channel parameter prediction. Based on GA+LS-SVM model, the time-varying channel parameters, such as delay spread, horizontal angle spread and vertical angle spread of receiver, were investigated and predicted accurately. Moreover, the GA+LS-SVM model was compared with back propagation neural network and traditional LS-SVM algorithms to verify the effectiveness of the algorithm. In summary, with limited amount of data the GA based LS-SVM model can better adapt to non-linear time-varying channel to realize the accurate prediction of nonlinear time-varying channel parameters.
第5代移动通信系统是近年来国内外研究的热点[1],特别是热点地区出现的大量移动的散射体,使得无线电波在其中的传输受到多种因素的影响,导致时变无线信道的预测缺乏准确性,因此受到广泛的研究关注.目前,国内外主流的建模思想还是基于几何的随机统计模型(GSCM, geometry-based stochastic model)[2-3],GSCM相比确定性模型复杂度较低,对不考虑具体环境物理特征情况下的系统级仿真和设计有应用价值,但在具体的链路设计及其仿真中常会与实际环境测试结果有大的偏差,难以解释很多物理现象,因此确定性模型也逐渐引起了大家的关注.确定性模型在给定的物理环境下,通过对电波传播的确定性计算进行仿真,但需要考虑特定传播场景和详尽的环境描述,计算量很大[4-6].
与此同时,国内外就机器学习算法中的支持向量机(SVM, support vector machine)与神经网络在无线通信方面展开了相应的学习[6].因为神经网络多是从生物仿生学的角度建立模型,而SVM作为一项通用的学习方法因其较为完备的理论基础摆脱了这一束缚.相较于现有的信道资源分配技术[7],SVM在建模和辨识、信道检测、衰落信道预测和信道估计以及非线性均衡等方面得到广泛的应用,并取得了良好的效果[8-13].但是,目前在信道参数预测方面的相关研究较少,在已有的相关文献中用于建模的训练验证数据多为仿真数据而非实测数据[14],因此基于实测数据的信道建模结果才更具说服性.
基于2.55 GHz室外微蜂窝场景的测量数据,将最小二乘支持向量机(LS-SVM, least square support vector machine)应用于信道参数的建模中,并利用遗传算法(GA, genetic algorithm)对模型中的超参数选择进行了优化,建立了基于GA的LS-SVM信道参数预测模型.对实际测量的信道参数如时延扩展、接收端的水平角度扩展和垂直角度扩展的数据特征进行预测学习,并通过与实际信道建模中最为常用的反向传播(BP, back propagation)神经网络算法和传统的LS-SVM进行对比,以验证算法的有效性.
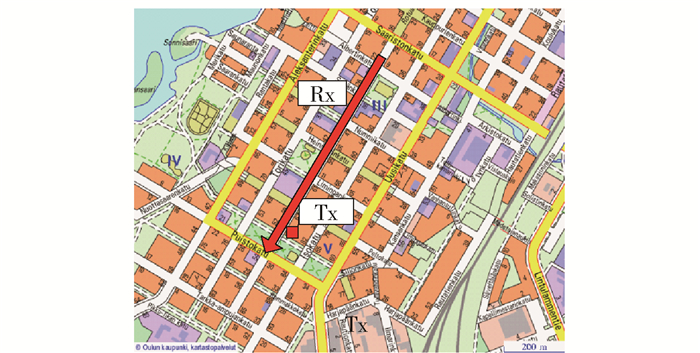
1 测量环境与测量系统所选用的2.55 GHz市区微蜂窝测量数据来自于实验室参与欧洲WINNER项目期间[15],在芬兰奥卢市区的实测数据.在测量中,收发端使用了多输入多输出(MIMO, multiple-input multiple-output)天线,全向阵列(ODA, omni-directional array)天线和16单元平面阵列天线(UPA, uniform planner array)分别用在发、送两端,如图 1所示.发射端与接收端分别使用了48个和16个双极化天线单元. 图 2所示为测量场景,在测试中发射端(Tx)固定,接收端(Rx)放置于小车上,以10 km/h的速度沿着视距路径移动. Tx与Rx的高度分别为8 m和1.7 m.系统参数设置见表 1.信道测试系统采用Elektrobit公司的Propsound时域信道探测仪.

|
图 1 测试系统天线 |
|
图 2 测量场景 |
|
|
表 1 测量系统参数 |
LS-SVM将二次规划问题转变为线性方程组的求解,速度因此大大提高.即将平方项作为其优化指标,并在处理迭代运算问题时,减小了对非线性系统预测回归计算的复杂程度.
LS-SVM通过训练数据对嵌入空间内未知函数f(·)进行拟合即可解决预测问题,即
| $ \begin{array}{*{20}{c}} {{x_k} = f\left( {{x_{k - m}}, \cdots , {x_{k - 2}}, {x_{k - 1}}} \right) = }\\ {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\phi \left( {\left[ {{x_{k - m}}, \cdots , {x_{k - 2}}, {x_{k - 1}}} \right]} \right) + b} \end{array} $ | (1) |
其中:ϕ(·)为实数集在特征空间中的一个非线性映射,ω∈Rn为输出权重向量,b∈R为偏差项,k与m为常数,表示模型中的输入个数和迭代数.当‖ω‖2/2取得最小值时,预测点离所求的最优超平面距离最小,即将寻求最优超平面的问题转化为求解一个带约束条件的二次凸规划问题,且优化目标为(1/2)ωTω,对应的优化目标函数为[11, 13]
| $ \left. {\begin{array}{*{20}{l}} {\min J(\omega , \xi ) = \frac{1}{2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} + \frac{\gamma }{2}\sum\limits_{i = 1}^k {\xi _i^2} }\\ {{\rm{ s}}{\rm{.t}}{\rm{.}}\;\;\;{y_i} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\phi \left( {{x_i}} \right) + b + {\xi _i}, i = 1, 2, \cdots , k} \end{array}} \right\} $ | (2) |
其中:ξi为松弛变量,其作用是当样本线性不可分时,可用来弱化约束条件,且松弛变量满足条件ξi≥ 0, i=1, 2, …, m;b为偏差;γ为正则化参数,是可调整量,是标准SVM中的惩罚因子,通过调节γ的取值让间隔(1/2)ωTω最大化和松弛变量ξi这两者条件得到平衡.
利用Lagrange函数求解上述优化问题,即
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\boldsymbol{\omega }}, b, {\xi _i}, {\alpha _i}} \right) = \frac{1}{2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} + \frac{\gamma }{2}\sum\limits_{i = 1}^N {\xi _i^2} - }\\ {\sum\limits_{i = 1}^N {{\alpha _i}} \left( {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{x_i}} \right) + b + {\xi _i} - {y_i}} \right)} \end{array} $ | (3) |
根据库恩塔克(KKT, Karush-Kuhn-Tucker)条件分别对ω、b、ξi、αi求偏导,消除ω、ξ,可得
| $ \left[ {\begin{array}{*{20}{c}} 0&{{\mathit{\boldsymbol{\nu }}^{\rm{T}}}}\\ \mathit{\boldsymbol{\nu }}&{\mathit{\boldsymbol{X}} + \frac{1}{\gamma }\mathit{\boldsymbol{I}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} b\\ \mathit{\boldsymbol{\alpha }} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0\\ \mathit{\boldsymbol{Y}} \end{array}} \right] $ | (4) |
其中:v=[1 1 … 1]T,I为N阶单位矩阵,α=[α1 α2 … αN]T,Y=[y1 y2 … yN]T,αi和yi分别为Lagrange算子和模型预测输出,X为N阶方阵.按照Mercer条件,φ(·)和核函数K(·, ·)存在映射,则其第i行第j列的元素kij=φ(xi)T(xj)=K(xi, xj),即高维空间的内积运算可转化为低维空间的核函数,则LS-SVM的预测决策函数可以描述为[16]
| $ f(x) = \sum\limits_{i = 1}^N {{\alpha _i}} K\left( {{x_i}, {x_j}} \right) + b $ | (5) |
其中αi与b可以通过训练数据集由式(2)~(4)求得.
在模型中,正则化参数γ和核函数K(·, ·)的核参数σ的选择对LS-SVM模型的好坏有重要影响,合适的超参数能够在很大程度上提升LS-SVM模型的性能.相较于传统模型中的网格搜索法,笔者采用GA二进制编码[17].利用GA算法选取参数包括以下5个步骤.
1) 确定交叉与变异的编码方式.对交叉和变异进行的是使用最为简单广泛的二进制编码,并进行初始化.通过以上操作,可将原始的输入空间映射到遗传空间中.
2) 设置遗传算法的初始基本参数.遗传算法中包含的初始参数有群数个数、最大迭代次数、交叉概率、变异概率等.这些参数在进行算法寻优时需根据输入样本的大小进行手动设置,确定适应度函数.由于在遗传算法中需对适应度函数的输出值进行大小比较,并进行排序,概率选择,为了减小计算量,提高运算速度,通常要求适应度函数的输出值为正值.
3) 依照遗传流程方法,对初始的父本种群进行选择、交叉和变异,得到新的子种群.
4) 判断子种群是否达到设定的精度要求,若满足精度要求,则将种群中的个体输出作为算法寻优的最优解;否则返回到步骤3),在此基础上需要判断该种群的种群数量是否达到设置的最大遗传阈值.
5) 将得到的最优个体进行解码,作为问题的最优解.
3 GA+LS-SVM信道建模结果分析 3.1 GA+LS-SVM模型信道参数分析基于GA优化的LS-SVM模型建立包括4个步骤.
1) 确定输入变量和输出变量.将包含时延扩展(DS,delay spread)在内的5个信道参数分为训练数据和验证数据,并将训练数据进行处理分组,同时进行归一化处理.
2) 确定核参数σ和正则化参数γ两个超参数.在输入输出变量的基础上,使用GA确定2个超参数.
3) 建立LS-SVM预测模型.将训练数据代入式(2)~式(4)中,通过训练计算得到最优化的Lagrange算子α和偏差b.最终根据式(5)得到决策函数.
4) 预测新的函数值.将测试数据代入模型f(x)中,得到相应的测试输出,通过评价指标判断模型预测性能的优劣.
将信道测试参数分为训练数据和验证数据.测试数据的选取量将影响到LS-SVM的学习程度和模型的精确度,目前在选取训练样本的数据上并没有统一的标准,一般选取总数据的70%作为训练样本[18].笔者选取的信道参数每个数据样本点均为2 104个,选取前1 472个点作为训练样本,后632个点作为测试样本.另外,将训练样本数据进行分组,将前5组数据作为输入,第6组数据作为输出,即可得训练样本输入与输出矩阵,见式(6)[16].
如上文所述,利用GA算法对超参数进行选取时,根据样本大小设置GA算法中的参数如下:种群个数初始为20,进化最大迭代次数为200,交叉概率为0.25,变异概率为0.005.在适应度函数的选取上,选择训练输出值和原始值之间均方误差的倒数作为适应度函数.
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{x}}_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_5}}\\ {{x_2}}&{{x_3}}& \cdots &{{x_6}}\\ \vdots & \vdots & \cdots & \vdots \\ {{x_{n - 6}}}&{{x_{n - 5}}}& \cdots &{{x_{n - 1}}} \end{array}} \right]}\\ {\mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}}\\ \vdots \\ {{y_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_6}}\\ {{x_7}}\\ \vdots \\ {{x_n}} \end{array}} \right]} \end{array} $ | (6) |
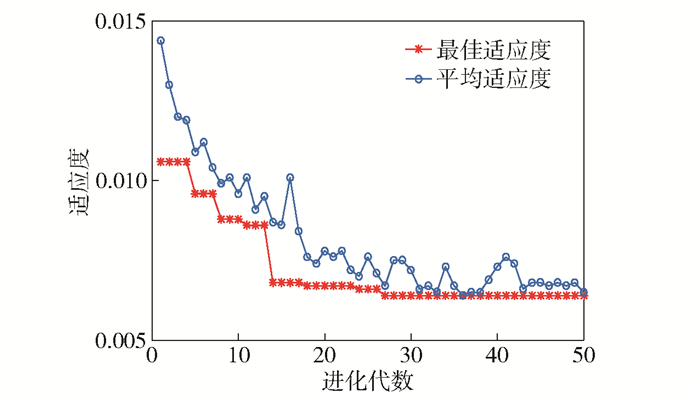
图 3所示为寻优过程中适应度函数变化曲线.可见,在参数寻优的过程中,当进化代数较小时(< 15),最佳和平均适应度有差异.随着进化代数的增加,平均适应度将逐渐趋同于最佳适应度.
|
图 3 适应度变化曲线 |
表 2所示为信道参数通过GA算法寻优所得的最佳核参数σ和最佳正则化参数γ.值得一提的是,超参数代表模型建立寻优过程中对模型精度的缩放程度,与原始数据并无直接关系.
|
|
表 2 最佳超参数 |
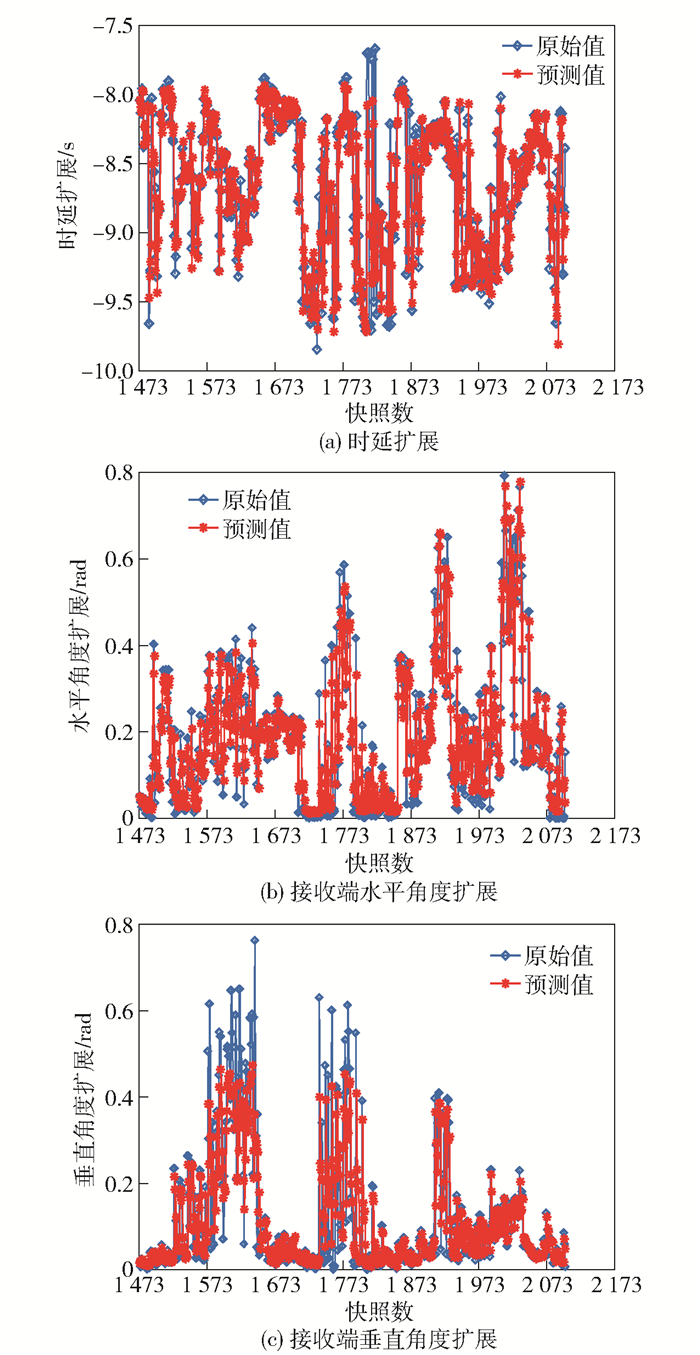
图 4所示为经GA优化后LS-SVM的各个信道参数,包括时延扩展、接收端水平角度扩展和垂直角度扩展的预测值与测试值.由图可见,预测值和原始(测试)值非常接近,如时延扩展和接收端水平角度扩展两者数据几乎重叠.值得注意的是,相比于水平角度扩展,接收端垂直角度扩展的预测值与原始值略有差异.这是由于发送端用的是全向阵列天线,而接收端所用的16单元平面阵列天线对垂直角度扩展影响较大,因此原始数据的非线性程度加大,从而导致在数据量较小的情况下,LS-SVM的预测值与原始数据的拟合程度降低.由图 4可见,基于GA优化的LS-SVM模型可以较好地学习信道参数之间的内在数据特征,在有限训练数据的条件下可预测出未来数据.即GA+LS-SVM模型在数据量较小的情况下对信道参数的变化有良好的适应性.对于非线性信道,经GA算法优化后的LS-SVM模型可取得较好的预测效果.
|
图 4 基于GA+LS-SVM模型的信道参数 |
目前对于神经网络的研究较为广泛,例如:卷积神经网络、递归神经网络以及文本卷积神经网络等,但是考虑到本文现有的信道测量数据样本的数据量的大小以及计算开销,利用结构简单的BP神经网络进行信道参数的建模即可满足精度要求[17].因此,为了验证GA+LS-SVM用于对信道参数进行建模的有效性,将对信道延时扩展用传统的LS-SVM模型与BP神经网络模型分别进行预测分析.
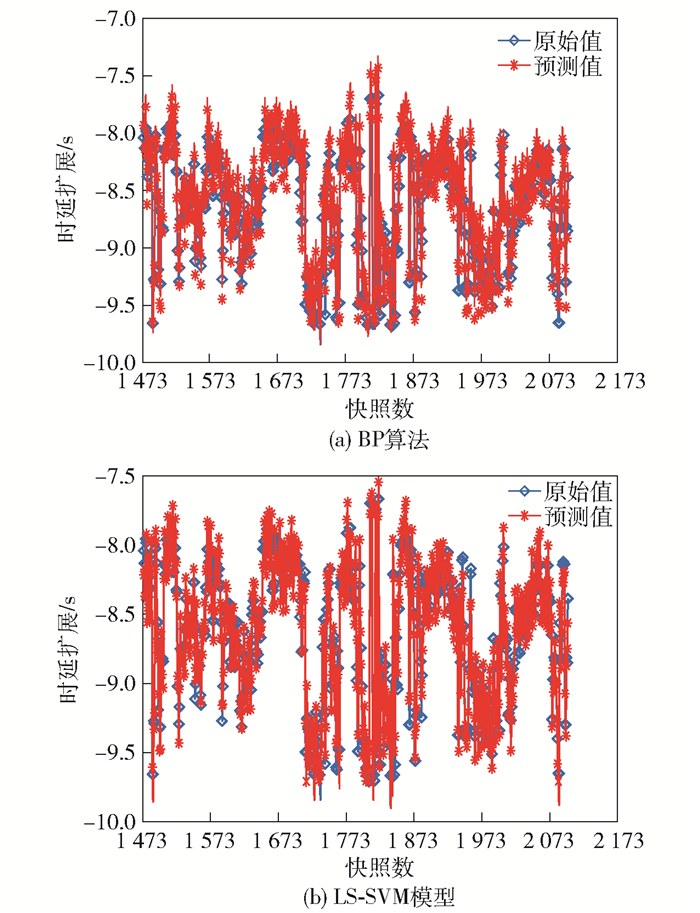
笔者采用的BP神经网络为三层网络结构,分别为输入层、隐层与输出层,其中隐层的神经元有500个;与此同时,传统的LS-SVM参数寻优所采用的最为简单的网格搜索法以此确定正则化参数和核参数,如图 5所示.结果表明,2种模型都能较精确地反映原始数据,即信道参数(时延扩展)随时间变化的规律.
|
图 5 预测结果对比 |
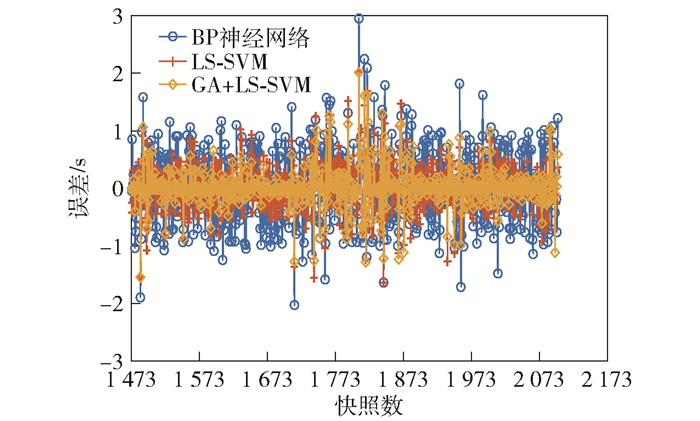
图 6所示为GA+LS-SVM模型、LS-SVM与BP神经网络模型预测结果的残差.可见,GA+LS-SVM的预测模型所得结果最好(误差最小).
|
图 6 预测结果残差 |
为了衡量GA+LS-SVM的有效性,主要考虑预测误差与计算时间2个指标,如表 3、表 4所示. 表 3所示为基于BP神经网络、LS-SVM和GA+LS-SVM三种算法的平均相对误差(MAPE,mean absolute percentage error)、均方根误差(RMSE,root mean square error)以及相关系数r.从表 3可见,通过GA+LS-SVM预测的参数效果最好,其次为LS-SVM,然后是BP神经网络模型.即通过GA+LS-SVM预测的MAPE和RMSE最小,而相关系数r最大.值得注意的是,相比其他几个信道参数,垂直角度扩展的预测效果较差,即平均相对误差和均方根误差较大,而相关系数较小,MAPE为0.154 6, RMSE为0.309 8,相关系数r为0.899 4.
|
|
表 3 预测误差表 |
|
|
表 4 运算时间 |
表 4所示为基于BP神经网络、LS-SVM和GA+LS-SVM三种算法的运算时间.从表 4可见,GA+LS-SVM运算的时间最短,而LS-SVM与BP神经网络模型的运行时间相差无几.值得注意的是,相比其他几个信道参数,垂直角度扩展的预测时间最长,三者的运算时间分别为135.6 s、156.5 s、170.5 s.
由此可见, 基于GA算法的LS-SVM信道模型在数据量较小的情况下能较好地学习信道参数的内在数据特征,并进行精准预测.另外GA+LS-SVM模型在保证精确度和运行时间的基础上,既能克服神经网络出现的陷入局部极值问题,又能解决传统LS-SVM在超参数寻优过程中运行时间较长的问题.
4 结束语基于2.55 GHz室外无线信道测量数据,将机器学习中的LS-SVM方法应用于时变信道参数的建模中.建立了基于GA优化的LS-SVM信道参数预测模型,并与BP神经网络算法与传统LS-SVM模型的预测结果进行了比较.具体来讲,利用基于GA优化的LS-SVM模型对信道参数如时延扩展、接收端的水平角度扩展和垂直角度扩展的数据特征进行了学习.结果表明,经GA优化的LS-SVM模型信道参数的预测值与实际测量值非常吻合. GA+LS-SVM算法的预测结果非常好,即平均相对误差及均方根误差较小,信号相关系数较大.值得注意的是,相比于接收端水平角度扩展,接收端垂直角度扩展的预测值与测量值略有差异.这是由于发送端用的是全向阵列天线,而接收端所用的16单元平面阵列天线对垂直角度扩展影响较大.因此,原始数据的非线性程度加大,从而导致在数据量较小的情况下,LS-SVM的预测值与原始数据的拟合程度降低.总之,基于遗传算法GA优化的LS-SVM模型在数据量较小的情况下对信道参数的变化有良好的适应性,对于非线性时变信道可取得满意的预测效果.
| [1] |
Jamsa T, Koysti P, Kusume K, et al. Initial channel models based on measurements[EB/OL]. Europe: Seventh Framework Program, 2014(2014-04-30)[2019-01-10]. https://www.metis2020.com/wp-content/uploads/deliverables/METIS_D1.2_v1.pdf.
|
| [2] |
Jiang Hao, Zhang Zaichen, Dang Jian, et al. A novel 3-D massive MIMO channel model for vehicle-to-vehicle communication environments[J]. IEEE Transactions on Communications, 2018, 66(1): 79-90. DOI:10.1109/TCOMM.2017.2751555 |
| [3] |
江浩, 张在琛, 党建, 等. 三维空间非平稳车载几何信道模型的研究分析[J]. 电子学报, 2018, 46(5): 1265-1268. Jiang Hao, Zhang Zaichen, Dang Jian, et al. Analysis of 3D geometry-based models for non-stationary vehicle-to-vehicle channels[J]. Acta Electronica Sinica, 2018, 46(5): 1265-1268. DOI:10.3969/j.issn.0372-2112.2018.05.037 |
| [4] |
Karedal J, Tufvesson F, Czink N, et al. Measurement-based modeling of vehicle-to-vehicle MIMO channels[C]//IEEE International Conference on Communications. New York: IEEE Press, 2009: 1-6.
|
| [5] |
Guan K, Ai B, Nicolas M, et al. On the influence of scattering from traffic signs in vehicle-to-X communications[J]. IEEE Trans Veh Technol, 2016, 65(8): 5835-5849. DOI:10.1109/TVT.2015.2476335 |
| [6] |
顾华来.机器学习在无线通信中的应用研究[D].南京: 南京大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10284-1012375770.htm
|
| [7] |
谢朝臣, 谭晓衡, 刘琴, 等. 基于空间信道控制方式的频谱感知资源分配技术[J]. 北京邮电大学学报, 2019, 42(1): 87-92. Xie Chaochen, Tan Xiaoheng, Liu Qin, et al. Investigation on spectral aware resource allocation technology based on spatial channel controlling[J]. Journal of Beijing University of Posts and Telecommunications, 2019, 42(1): 87-92. |
| [8] |
朱亚辉, 黄襄念. SVM方法在模式识别应用领域中的发展与研究[J]. 现代计算机(专业版), 2015(6): 20-24. Zhu Yahui, Huang Xiangnian. Development and research on the SVM methods in the field of pattern recognition applications[J]. Modern Computer, 2015(6): 20-24. |
| [9] |
Charrada A, Samet A. LTE downlink channel estimation based on artificial neural network and complex support vector machine regression[C]//2016 4th International Conference on Control Engineering & Information Technology (CEIT). New York: IEEE Press, 2016: 101-110.
|
| [10] |
史通, 王洁, 罗畅, 等. 机器学习在频谱大数据分析与处理上的应用[J]. 火力与指挥控制, 2018, 43(6): 47-51. Shi Tong, Wang Jie, Luo Chang, et al. Application of machine learning in big spectrum data analyzing and processing[J]. Fire Control & Command Control, 2018, 43(6): 47-51. DOI:10.3969/j.issn.1002-0640.2018.06.009 |
| [11] |
相征, 张太镒, 孙建成. 基于最小二乘支持向量机的非线性系统建模[J]. 系统仿真学报, 2006, 18(9): 2684-2687. Xiang Zheng, Zhang Taiyi, Sun Jiancheng. Modelling of nonlinear systems based on recurrent least squares support vector machines[J]. Journal of System Simulation, 2006, 18(9): 2684-2687. DOI:10.3969/j.issn.1004-731X.2006.09.077 |
| [12] |
周向军. 基于最小二乘支持向量机的无线网络信道检测[J]. 计算机系统应用, 2018, 27(5): 151-155. Zhou Xiangjun. Channel detection of wireless networks based on least squares support vector machines[J]. Computer Systems & Applications, 2018, 27(5): 151-155. |
| [13] |
相征, 张太镒, 孙建成. 基于最小二乘支持向量机的衰落信道预测算法[J]. 电子与信息学报, 2006, 28(4): 671-674. Xiang Zheng, Zhang Taiyi, Sun Jiancheng. Prediction algorithm for fast fading channels based on recurrent least squares support vector machines[J]. Journal of Electronics & Information Technology, 2006, 28(4): 671-674. |
| [14] |
郗茜.基于LS-SVM的半圆拱形巷道无线信道建模与预测[D].西安: 西安科技大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10704-1017725404.htm
|
| [15] |
Kyosti P, Meinila J, Hentila L, et al. Final report on link level and system level channel models[EB/OL]. Europe: Information Society Technologies, 2008(2008-02-04)[2019-01-10]. https://www.researchgate.net/publication/259900906_IST-4-027756_WINNER_II_D112_v12_WINNER_II_channel_models.
|
| [16] |
孙建成, 郑崇勋, 周亚同, 等. 基于RLS-SVM的OFDM信道估计算法[J]. 系统仿真学报, 2009, 21(13): 4009-4013, 4018. Sun Jiancheng, Zheng Chongxun, Zhou Yatong, et al. Channel estimation algorithm of OFDM system based on RLS-SVM[J]. Journal of System Simulation, 2009, 21(13): 4009-4013, 4018. |
| [17] |
董志翔, 赵宜升, 黄锦锦, 等. 基于支持向量机的高速铁路通信系统信道预测算法[J]. 电子技术应用, 2018, 44(4): 117-121. Dong Zhixiang, Zhao Yisheng, Huang Jinjin, et al. Support vector machine for channel prediction in high-speed railway communication systems[J]. Application of Electronic Technique, 2018, 44(4): 117-121. |
| [18] |
张静, 金石, 温朝凯, 等. 基于人工智能的无线传输技术最新研究进展[J]. 电信科学, 2018, 34(8): 46-55. Zhang Jing, Jin Shi, Wen Chaokai, et al. An overview of wireless transmission technology utilizing artificial intelligence[J]. Telecommunications Science, 2018, 34(8): 46-55. |



