2. 北京大学 物理学院, 北京 100871
为了减小系统非线性和噪声对参数辨识效果的影响,采用缺失变量的高阶关联矩阵方法(HOCC),以处于混沌状态的蔡氏电路为研究对象,分别对模拟蔡氏电路以及存在噪声的单个实验蔡氏电路和耦合实验蔡氏电路进行动力学参数辨识.研究结果表明,该方法在蔡氏电路电感电流未知情况下进行参数辨识是有效的,同时对噪声具有很好的鲁棒性.所得的参数辨识结果和电路标定参数的相对差距均能在20%的范围之内.该研究结果可以为蔡氏电路中器件参数测量提供参考依据,并能进一步应用到其他网络结构参数辨识实验中.
2. School of Physics, Peking University, Beijing 100871, China
In order to reduce the influence of system nonlinearity and noise on the effect of parameter identification, the high-order correlation computations (HOCC) with missing variables and noise is used to identify the dynamic parameters of real chaotic Chua's circuit, based on both simulation and experimental data of a single chua's circuit and a coupled chua's circuit. The results showed that the relative errors between identifications and calibration parameters of the experiments can be controlled within 20%, which means HOCC not only has good robustness to noise but also solves the problem produced by the missing data of the current of inductance. This work provided a benchmark for the measurement of instrument parameters of Chua's circuit, and could further apply on the parameter identification of other complicated networks.
通过数据推断其背后动力学方程的未知参数,已经成为近些年人们研究的重点,该过程被称作参数辨识[1].明确动力学行为,对于预测信息传播和社交网络中的病毒传播等具有很大的意义[2],如Zheng等[3]通过自适应参数辨识方法准确辨识了耦合循环动力神经网络的未知参数.但由于实际系统存在非线性和噪声,有时候也会缺失部分变量,使得利用数据进行参数辨识研究具有一定的挑战性[4].目前较为成熟的方法往往忽略噪声的影响或者只考虑线性动力学,具有很大的局限性,在实际中缺乏指导意义[5-6].
笔者采用Chen等[7-8]提出的一种方法,即高阶关联矩阵方法(HOCC, high-order correlation computations)来对复杂系统进行逆问题研究,并以蔡氏电路[9-11]为研究对象,对处于混沌状态下缺失电流数据的蔡氏电路系统,分别基于模拟电路和实际电路中的数据进行动力学参数辨识,得到了与标定参数相符的辨识结果.
1 HOCC方法在蔡氏电路中的应用本节主要介绍HOCC方法在蔡氏电路中的实现过程,将分为HOCC方法实现参数辨识、在单个蔡氏电路中的应用、在耦合蔡氏电路中的应用3个方面.
1.1 HOCC方法实现参数辨识非线性系统的动力学通常可以用以下含有噪声的非线性方程组描述:
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{x}}\left( t \right)}}{{{\rm{d}}t}}{\rm{ = }}\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{x}}\left( t \right)} \right) + \mathit{\varGamma }\left( t \right) $ | (1) |
其中:x=(x1, x2, …, xN)T,f=(f1, f2, …, fN)T,Γ=(Γ1, Γ2, …, ΓN)T,xi(t)为i节点的时间序列,Γi(t)为i节点上的噪声.
微分和积分准确性都是依赖时间步长的大小,但如果对式(1)进行积分处理,等号右边可能因为积分的存在加大噪声的影响,所以对微分的处理就用某个时刻前后值的差除以步长代替,即
| $ \frac{{{\rm{d}}{\mathit{x}_\mathit{i}}\left( t \right)}}{{{\rm{d}}t}} \approx \frac{{{\mathit{x}_\mathit{i}}\left( {t + {\rm{d}}\mathit{t}} \right) - {\mathit{x}_\mathit{i}}\left( t \right)}}{{{\rm{d}}\mathit{t}}} $ |
并且噪声常常近似为白噪声,即
| $ \left\langle {{\mathit{\varGamma }_\mathit{i}}\left( t \right)} \right\rangle = 0,\left\langle {{\mathit{\varGamma }_\mathit{i}}\left( t \right){\mathit{\varGamma }_\mathit{j}}\left( {t'} \right)} \right\rangle = {Q_{ij}}\left( \mathit{\boldsymbol{x}} \right){\delta _{ij}}\delta \left( {t - t'} \right) $ |
HOCC方法中假设fi可以按一定的基底形式展开:
| $ {f_i}\left( {\mathit{\boldsymbol{x}}\left( t \right)} \right) = \sum\limits_{\mu = 1}^\infty {{A_{i,\mu }}{Y_{i,\mu }}\left( {\mathit{\boldsymbol{x}}\left( t \right)} \right)} ,i = 1,2, \cdots ,\mathit{N} $ |
对于噪声,差时相关方法可以有效地对其进行过滤.式(1)两边同乘Y(x(t-τ))T,可以得到一个矩阵方程:
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{AC}} + {\rm{ }}\left\langle {{\mathit{\varGamma }_\mathit{i}}\left( t \right)\mathit{\boldsymbol{Y}}{{\left( {\mathit{\boldsymbol{x}}\left( {t - \tau } \right)} \right)}^{\rm{T}}}} \right\rangle $ |
其中
| $ \mathit{\boldsymbol{B}} = \left\langle {\frac{{{\rm{d}}{\mathit{x}_\mathit{i}}\left( t \right)}}{{{\rm{d}}t}}\mathit{\boldsymbol{Y}}{{\left( {\mathit{\boldsymbol{x}}\left( {t - \tau } \right)} \right)}^{\rm{T}}}} \right\rangle $ |
| $ \begin{array}{*{20}{c}} \mathit{\boldsymbol{C}}{\rm{ = }}\left\langle {\mathit{\boldsymbol{Y}}\left( {\mathit{\boldsymbol{x}}\left( t \right)} \right)\mathit{\boldsymbol{Y}}{{\left( {\mathit{\boldsymbol{x}}\left( {t - \tau } \right)} \right)}^{\rm{T}}}} \right\rangle \\ {\left\langle {{\mathit{\Gamma }_i}(t)\mathit{\boldsymbol{Y}}{{(\mathit{\boldsymbol{x}}(t - \tau))}^{\rm{T}}}} \right\rangle \approx 0} \end{array} $ |
进而系数矩阵可以表示为
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{C}}^{ - 1}} $ |
通过对Y(x(t))进行适当地截断,在x(t),Y(x(t)),Y(x(t-τ))已知的情况下,B和C两个矩阵即可被很精确地求出,进而可以得到具体的A.至此,HOCC方法通过将方程组转换为矩阵计算实现了计算方便和去除噪声以及参数辨识的作用.
1.2 单个电路参数辨识蔡氏电路是由Chua在1983年提出的,因其简洁性和代表性而成为研究非线性电路中混沌的典范[9-11].该电路是由线性电阻﹑电容、电感和非线性“蔡氏二极管”组成的三阶自治电路,通过改变电路参数,可以实现丰富的动力学现象,被广泛地应用在实际生活中. 图 1为蔡氏电路的电路图和非线性电阻的I-U曲线.

|
图 1 蔡氏电路 |
图 1中,L为电感,C1、C2为电容,R为可变电阻器,NR为非线性电阻, Ga、Gb为内外折线的斜率,Bp为折线拐点.
根据电路原理,蔡氏电路可由以下方程组进行描述:
| $ {C_1}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{\rm{1}}}}}}}{{{\rm{d}}t}} = \frac{1}{R}\left( {{u_{{c_2}}} - {u_{{c_1}}}} \right) - f\left( {{u_{{c_1}}}} \right) + {\mathit{\Gamma }_{\rm{1}}}\left( t \right) $ | (2) |
| $ {C_2}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{\rm{2}}}}}}}{{{\rm{d}}t}} = \frac{1}{R}\left( {{u_{{c_1}}} - {u_{{c_2}}}} \right) + {i_L} + {\mathit{\Gamma }_{\rm{2}}}\left( t \right) $ | (3) |
| $ \frac{{{\rm{d}}{i_L}}}{{{\rm{d}}t}} = \frac{1}{L}\left( { - {u_{{c_2}}}} \right) + {\mathit{\Gamma }_{\rm{3}}}\left( t \right) $ | (4) |
其中:uc1为C1两端的电压,uc2为C2两端的电压,iL为通过电感L的电流,Γi(t), i=1, 2, 3为系统噪声,在这里将其近似为白噪声,f(uc1)为描述非线性电路NR的I-U特性的多项式:
| $ f\left( {{u_{{c_1}}}} \right) = {G_b}{u_{{c_1}}} + \frac{1}{2}\left( {{G_a} - {G_b}} \right)\left( {\left| {{u_{{c_1}}} + {B_p}} \right| - \left| {{u_{{c_1}}} - {B_p}} \right|} \right) $ |
在电感的电流数据缺失的情况下,参数识别需要运用缺失部分变量情况下的HOCC方法来进行.其中,式(2)不涉及电流,公式保持不变,式(4)代入式(3)求导后的等式中,得到
| $ \begin{array}{*{20}{c}} {{C_1}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{\rm{1}}}}}}}{{{\rm{d}}t}} = \frac{1}{R}\left( {{u_{{c_2}}} - {u_{{c_1}}}} \right) - f\left( {{u_{{c_1}}}} \right) + {\mathit{\Gamma }_{\rm{1}}}\left( t \right)}\\ {{C_2}\frac{{{{\rm{d}}^{\rm{2}}}{\mathit{u}_{{\mathit{c}_{\rm{2}}}}}}}{{{\rm{d}}{t^2}}} = \frac{1}{R}\left( {\frac{{{\rm{d}}{\mathit{u}_{{\mathit{ }_{\rm{1}}}}}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{\rm{2}}}}}}}{{{\rm{d}}t}}} \right) + \frac{1}{L}\left( { - {u_{{c_2}}}} \right) + }\\ {\mathit{\Gamma }{\mathit{'}_2}\left( t \right) + {\mathit{\Gamma }_{\rm{3}}}\left( t \right)} \end{array} $ | (5) |
对于式(2)基底的选取,从实际方程出发,选择
| $ \mathit{\boldsymbol{Y}}\left( t \right) = \left( {{u_{{c_1}}},{u_{{c_2}}},\left| {{u_{{c_1}}} + {B_p}} \right|,\left| {{u_{{c_2}}} - {B_p}} \right|} \right) $ |
作为基底.此时方程可以表示为
| $ \frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{\rm{1}}}}}}}{{{\rm{d}}t}} = \mathit{\boldsymbol{AY}} $ |
A为基底Y前的系数.对变形后的等式两边同乘基底的差时转置,即
| $ \mathit{\boldsymbol{Y}}{\left( {t - \tau } \right)^{\rm{T}}} = {\left( {{u_{{c_1}}},{u_{{c_2}}},\left| {{u_{{c_1}}} + {B_p}} \right|,\left| {{u_{{c_1}}} - {B_p}} \right|} \right)^{\rm{T}}} $ |
进一步可以得到
| $ \mathit{\boldsymbol{B}}{\rm{ = }}\mathit{\boldsymbol{AC}} $ |
其中
| $ \mathit{\boldsymbol{B}} = \left\langle {\frac{{{\rm{d}}{u_{{c_1}}}}}{{{\rm{d}}t}}\mathit{\boldsymbol{Y}}{{\left( {t - \tau } \right)}^{\rm{T}}}} \right\rangle $ |
| $ \mathit{\boldsymbol{C}}{\rm{ = }}\left\langle {\mathit{\boldsymbol{YY}}{{\left( {t - \tau } \right)}^{\rm{T}}}} \right\rangle $ |
进而求出方程系数
| $ \mathit{\boldsymbol{A}}\mathit{ = }\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{C}}^{ - 1}} $ |
A中每项的值对应公式(2)的各个系数,即
| $ \left. {\begin{array}{*{20}{l}} {{A_1} = - \left( {\frac{1}{{R{C_1}}} + \frac{{{G_b}}}{{{C_1}}}} \right)}\\ {{A_2} = \frac{1}{{R{C_1}}}}\\ {{A_3} = \frac{{{G_a} - {G_b}}}{{ - 2{C_1}}}}\\ {{A_4} = \frac{{{G_a} - {G_b}}}{{2{C_1}}}} \end{array}} \right\} $ | (6) |
类似地,对于式(5)选取基底
| $ \mathit{\boldsymbol{Z}}\mathit{ = }\left( {\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{\rm{1}}}}}}}{{{\rm{d}}t}},\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{\rm{2}}}}}}}{{{\rm{d}}t}},{\mathit{u}_{{\mathit{c}_{\rm{2}}}}}} \right) $ |
也可以求出
| $ \mathit{\boldsymbol{E}}\mathit{ = }\left\langle {\frac{{{{\rm{d}}^{\rm{2}}}{\mathit{u}_{{\mathit{c}_{\rm{2}}}}}}}{{{\rm{d}}{t^2}}}\mathit{\boldsymbol{Z}}{{\left( {t - \tau } \right)}^{\rm{T}}}} \right\rangle $ |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}}\mathit{ = }\left\langle {\mathit{\boldsymbol{ZZ}}{{\left( {t - \tau } \right)}^{\rm{T}}}} \right\rangle }\\ {\mathit{\boldsymbol{D}} = \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{F}}^{ - 1}}} \end{array} $ |
D中每项的值,对应式(5)的各个系数,即
| $ {D_1} = \frac{1}{{R{C_2}}},{D_2} = - \frac{1}{{R{C_2}}},{D_3} = - \frac{1}{{L{C_2}}} $ | (7) |
由于实际电阻R的测量较为准确,在这里假设电阻R已知.利用式(6)和式(7)就可以求出蔡氏电路的其他5个参数:
| $ \left. {\begin{array}{*{20}{l}} {{C_1} = \frac{1}{{R{A_2}}},{C_2} = \frac{1}{{R{D_1}}},{G_a} = 2{A_4}{C_1} + {G_b}}\\ {{G_b} = - \left( {{A_1} + {A_2}} \right){C_1},L = - \frac{1}{{{D_3}{C_2}}}} \end{array}} \right\} $ | (8) |
耦合的蔡氏电路常常被用到加密系统中,主要方法是2个蔡氏电路通过单向耦合电路将信息掩盖到混沌信号中达到加密解密效果[12].其电路如图 2所示.
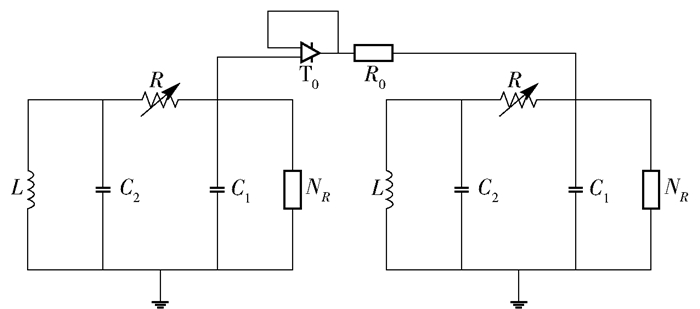
|
图 2 耦合蔡氏电路 |
图 2中,L为电感,C1、C2为电容,R、R0为可变电阻器,NR为非线性电阻,T0为射随器.
根据电路原理,2个蔡氏电路可建立以下方程:
| $ {C_{11}}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{11}}}}}}}}{{{\rm{d}}t}} = \frac{1}{{{R_1}}}\left( {{u_{{c_{12}}}} - {u_{{c_{11}}}}} \right) - f\left( {{u_{{c_{11}}}}} \right) + {\mathit{\Gamma }_{\rm{1}}}\left( t \right) $ | (9) |
| $ {C_{12}}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{12}}}}}}}}{{{\rm{d}}t}} = \frac{1}{{{R_1}}}\left( {{u_{{c_{11}}}} - {u_{{c_{12}}}}} \right) + {i_{{L_1}}} + {\mathit{\Gamma }_{\rm{2}}}\left( t \right) $ | (10) |
| $ \frac{{{\rm{d}}{i_{{L_1}}}}}{{{\rm{d}}t}} = \frac{1}{{{L_1}}}\left( { - {u_{{c_{12}}}}} \right) + {\mathit{\Gamma }_{\rm{3}}}\left( t \right) $ | (11) |
| $ \begin{array}{*{20}{c}} {{C_{21}}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{21}}}}}}}}{{{\rm{d}}t}} = \frac{1}{{{R_2}}}\left( {{u_{{c_{22}}}} - {u_{{c_{21}}}}} \right) - f\left( {{u_{{c_{21}}}}} \right) + }\\ {k\left( {{u_{{c_{11}}}} - {u_{{c_{21}}}}} \right) + {\mathit{\Gamma }_{\rm{4}}}\left( t \right)} \end{array} $ | (12) |
| $ {C_{22}}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{22}}}}}}}}{{{\rm{d}}t}} = \frac{1}{{{R_2}}}\left( {{u_{{c_{21}}}} - {u_{{c_{22}}}}} \right) + {i_{{L_2}}} + {\mathit{\Gamma }_{\rm{5}}}\left( t \right) $ | (13) |
| $ \frac{{{\rm{d}}{i_{{L_2}}}}}{{{\rm{d}}t}} = \frac{1}{{{L_2}}}\left( { - {u_{{c_{22}}}}} \right) + {\mathit{\Gamma }_{\rm{6}}}\left( t \right) $ | (14) |
其中:C11、C12、R1、L1分别为驱动电路的各个参数,C21、C22、R2、L2分别为响应电路的各个参数,k表示电路间的耦合强度,并且是单向耦合,这在实际电路中是通过一个射随器加可变电阻器实现的.
同样,仍然假设缺失电感电流I.将式(11)代入式(10)求导后的等式中,式(14)代入式(13)求导后的等式中得到
| $ \begin{array}{*{20}{c}} {{C_{11}}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{11}}}}}}}}{{{\rm{d}}t}} = \frac{1}{{{R_1}}}\left( {{u_{{c_{12}}}} - {u_{{c_{11}}}}} \right) - f\left( {{u_{{c_{11}}}}} \right) + {\mathit{\Gamma }_{\rm{1}}}\left( t \right)}\\ {{C_{12}}\frac{{{{\rm{d}}^{\rm{2}}}{\mathit{u}_{{\mathit{c}_{{\rm{12}}}}}}}}{{{\rm{d}}{t^2}}} = \frac{1}{{{R_1}}}\left( {\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{11}}}}}}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{12}}}}}}}}{{{\rm{d}}t}}} \right) + \frac{1}{{{L_1}}}\left( { - {u_{{c_{12}}}}} \right) + }\\ {\mathit{\Gamma }{\mathit{'}_2}\left( t \right) + {\mathit{\Gamma }_{\rm{3}}}\left( t \right)} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{C_{21}}\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{21}}}}}}}}{{{\rm{d}}t}} = \frac{1}{{{R_2}}}\left( {{u_{{c_{22}}}} - {u_{{c_{21}}}}} \right) - f\left( {{u_{{c_{21}}}}} \right) + }\\ {k\left( {{u_{{c_{11}}}} - {u_{{c_{21}}}}} \right) + {\mathit{\Gamma }_{\rm{4}}}\left( t \right)} \end{array}}\\ {{C_{22}}\frac{{{{\rm{d}}^{\rm{2}}}{\mathit{u}_{{\mathit{c}_{{\rm{22}}}}}}}}{{{\rm{d}}{t^2}}} = \frac{1}{{{R_2}}}\left( {\frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{21}}}}}}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}{\mathit{u}_{{\mathit{c}_{{\rm{22}}}}}}}}{{{\rm{d}}t}}} \right) + \frac{1}{{{L_2}}}\left( { - {u_{{c_{22}}}}} \right) + }\\ {\mathit{\Gamma }{\mathit{'}_5}\left( t \right) + {\mathit{\Gamma }_{\rm{6}}}\left( t \right)} \end{array} $ | (16) |
其中式(15)和式(5)的基底选择一样,对于式(16)在式(5)的基础上增加一项,即为
| $ \mathit{\boldsymbol{A}}\mathit{ = }\left( {{u_{{c_{21}}}},{u_{{c_{22}}}},\left| {{u_{{c_{21}}}} + {B_p}} \right|,\left| {{u_{{c_{22}}}} - {B_p}} \right|,{u_{{c_{21}}}} - {u_{{c_{22}}}}} \right) $ |
在这里,除了可以求出2个电路参数外,还可以求出耦合强度k的值,这样就能够得到耦合电路的全部动力学参数为
| $ \left. {\begin{array}{*{20}{l}} {{C_{11}} = \frac{1}{{{R_1}{A_2}}},{C_{12}} = \frac{1}{{{R_1}{D_1}}},{G_{a1}} = 2{A_4}{C_{11}} + {G_{b1}}}\\ {{G_{b1}} = - \left( {{A_1} + {A_2}} \right){C_{11}},{L_1} = - \frac{1}{{{D_3}{C_{12}}}}}\\ {{C_{21}} = \frac{1}{{{R_2}{A_2}}},{C_{22}} = \frac{1}{{{R_2}{D_1}}},{G_{a2}} = 2{A_4}{C_{21}} + {G_{b2}}}\\ {{G_{b2}} = - \left( {{A_1} + {A_2}} \right){C_{21}},{L_2} = - \frac{1}{{{D_3}{C_{22}}}},k = {\mathit{C}_{21}}{A_5}} \end{array}} \right\} $ | (17) |
考虑到实际电路标定的器件参数精确度不足,首先对计算机模拟蔡氏电路产生的数据采用HOCC方法进行参数辨识.在确认该方法在蔡氏电路中的适用性之后,再对采集实验电路混沌状态下的数据进行同样方法的参数辨识,来验证其在实验电路的适用性.
2.1 模拟电路选取混沌态下的一组电路参数:R=1 850 Ω, C1=10 nF, C2=100 nF, L=21.8 mH,Ga=-7.6×10-4 Ω-1, Gb=-4.1×10-4 Ω-1, Bp=1.6 V,并设定uc1、uc2、iL初始值分别为0.1 V、0、0,在计算机软件上根据式(2)~式(4)(此时Γi=0)模拟产生电容C1两端的电压和电容C2两端的电压,并分别为横纵坐标做出其相图(图 3(a)).运用1.2节中的HOCC方法选取基底后,按照式(8)辨识出电路参数,再以此进行仿真得到电容C1两端的电压和电容C2两端的电压以及相应的相图,如图 3(b)所示.然后利用了(辨识值-标定值)/标定值的结果绝对值得出误差,如表 1所示.进一步,实验电路中噪声的存在是难以避免的,利用HOCC方法在有噪声的条件下进行参数辨识效果如何也是受关注的问题.为此,模拟电路加入了高斯白噪声.式(2)~式(4)中,
| $ {\mathit{\Gamma }_\mathit{i}}\left( t \right) = \frac{{{D_i}}}{{{\rm{d}}t}}n $ |

|
图 3 模拟蔡氏电路相图 |
|
|
表 1 模拟电路误差 |
其中:Di为噪声强度,dt为模拟步长,n为一个服从正态分布的数.
为了使辨识效果更理想,首先对数据进行平滑处理,然后运用1.2节的方法得到参数方程,进一步得到的相图和辨识相图,如图 3(c)和3(d)所示.
比较图 3(a)和图 3(b)不难看出,两图的电压区间和相轨道基本一致,这说明HOCC方法能够在这种情况下有很好的参数辨识能力.此外,表 1也给出了关键电路标定与辨识值及其误差,充分说明了该方法对于模拟电路的参数辨识具有极高的精确度与可靠性.进一步地,通过图 3(c)、图 3(d)以及图 3(a)的比较可以看出,在噪声对系统产生较大干扰的情况下,HOCC方法也能很好地辨识出电路参数.这一点也可以由表 1的误差表说明.因此完全可以利用HOCC方法进行实验电路参数辨识.
2.2 单个实验电路对于实验电路,选择标定值为模拟电路选取数值的器件进行搭建[12],通过LCR-电桥表得到测量值,并逐步调节可变电阻使实验电路处于混沌状态,然后运用LabVIEW[13]进行数据采集. 图 4为实验电路相图和辨识后相图.
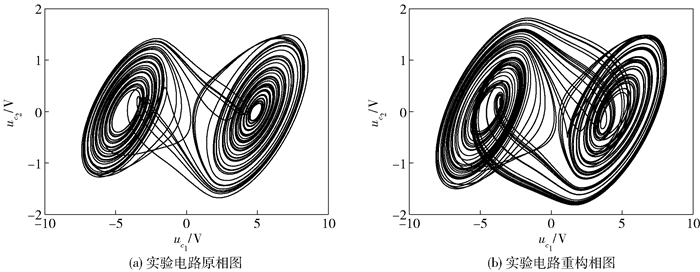
|
图 4 实验电路相图 |
从误差表 2可以看出,实验电路辨识的偏差比模拟电路辨识大,其原因可能是实验电路器件标定值的精度存在一定的偏差,同时实验电路中噪声更加复杂,采用处理白噪声的方法可能并不适用.从测量值和辨识值的比较中可以看出,该方法对器件参数的测量能够提供一定的参考性,而且从辨识后相图中可以看出HOCC方法能够在一定程度上复现出电压的轨迹,这对以后的研究也具有一定的意义.
|
|
表 2 实验电路误差 |
选取电容电感以及非线性电阻标定值都一样即为模拟实验中的数值,但是可变电阻大小不一样的2个耦合状态的蔡氏电路搭建成耦合电路[12].由于2个电路初值和可变电阻不同,所以2个电路处于不同的混沌状态,通过调节耦合器就可以改变2个电路的同步效果,图 5(a)和图 5(b)即为某个耦合强度下的相图,图 5(c)和图 5(d)为应用1.3节方法得到的结果相图.
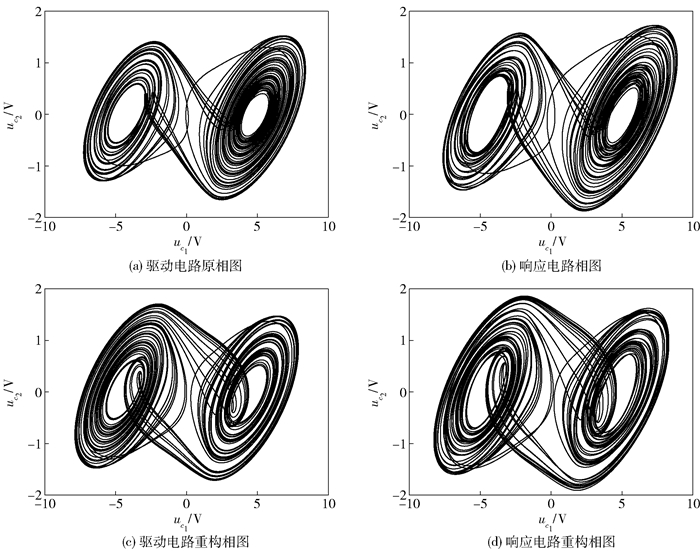
|
图 5 耦合蔡氏电路相图 |
从图 5的相图的运动轨迹和周期性可以看出,此时耦合强度下驱动单元和响应单元比较接近,从辨识后得到的相图来看二者也是很接近,从表 3和表 4的误差也可以看出,辨识值和标定值以及辨识值和测量值相差都很小,这都说明了HOCC方法对于实验耦合蔡氏电路辨识的有效性.
|
|
表 3 驱动电路误差 |
|
|
表 4 响应电路误差 |
利用HOCC方法辨识了缺失电流数据的实验蔡氏电路及其耦合系统的参数,克服了缺失变量和噪声处理的问题.重构得到的辨识结果与标定值的相对差距均在20%以内.期望利用辨识出的电路参数对仪器测量的参数进行比较修正,并进一步将该方法运用到其他未知的电路或者网络中,进而揭秘未知网络中各个节点之间的关系.
| [1] |
关新平, 彭海朋, 李丽香, 等. Lorenz混沌系统的参数辨识与控制[J]. 物理学报, 2001, 5050(1): 26-29. Guan Xinping, Peng Haipeng, Li Lixiang, et al. Parameters identification and control of lorenz chaotic system[J]. Acta Physica Sinica, 2001, 5050(1): 26-29. DOI:10.3321/j.issn:1000-3290.2001.01.005 |
| [2] |
Marbach D, Prill R J, Schaffter T, et al. Revealing strengths and weaknesses of methods for gene network inference[J]. Proceedings of the National Academy of Sciences, 2010, 107(14): 6286-6291. DOI:10.1073/pnas.0913357107 |
| [3] |
Zheng Mingwen, Li Lixiang, Peng Haipeng, et al. Parameters estimation and synchronization of uncertain coupling recurrent dynamical neural networks with time-varying delays based on adaptive control[J]. Neural Computing and Applications, 2016, 30(7): 2217-2227. |
| [4] |
Zhang Zhaoyang, Zheng Zhigang, Niu Haijing, et al. Solving the inverse problem of noise-driven dynamic networks[J]. Physical Review E, 2015, 91(1): 012814. DOI:10.1103/PhysRevE.91.012814 |
| [5] |
Daniels B C, Nemenman I. Automated adaptive inference of phenomenological dynamical models[J]. Nature Communications, 2015(6): 8133. |
| [6] |
Ching E S, Lai P Y, Leung C. Reconstructing weighted networks from dynamics[J]. Physical Review E, 2015, 91(3): 030801. DOI:10.1103/PhysRevE.91.030801 |
| [7] |
Chen Yang, Zhang Zhaoyang, Chen Tianyu, et al. Reconstruction of noise-driven nonlinear networks from node outputs by using high-ordercorrelations[J]. Scientific Reports, 2017(7): 44639. |
| [8] |
Chen Tianyu, Chen Yang, Yang Hujiang, et al. Reconstruction of dynamic structures of experimental setups based on measurable experimental data only[J]. Chinese Physics B, 2018, 27(3): 030503. DOI:10.1088/1674-1056/27/3/030503 |
| [9] |
Chua L O, Kocarev L, Eckert K, et al. Experiment chaos synchronization in chua's circuit[J]. Internationl Journal of Bifurcation and Chaos, 1992, 2(3): 705-708. DOI:10.1142/S0218127492000811 |
| [10] |
Kennedy M P. Three steps to chaos. Ⅰ[J]. IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 1993, 40(10): 640-656. |
| [11] |
Kennedy M P. Three steps to chaos. Ⅱ[J]. IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 1993, 40(10): 657-674. |
| [12] |
李海红, 代琼琳, 王世红, 等. 一种简单的基于蔡氏电路的数字加密通信实验[J]. 大学物理, 2006, 25(9): 39-42. Li Haihong, Dai Qionglin, Wang shihong, et al. A simple solution of digital secure communication based on chua's circuits[J]. College Physics, 2006, 25(9): 39-42. DOI:10.3969/j.issn.1000-0712.2006.09.012 |
| [13] |
蒋达娅, 肖井华. 基于LabVIEW的物理实验在学生素质培养上的作用[J]. 实验技术与管理, 2012, 29(3): 304-307. Jiang Daya, Xiao Jinghua. Function of physies experiment for student's quality cultivation based on LabVIEW[J]. Experimental Technology and Management, 2012, 29(3): 304-307. |



