2. 咸阳师范学院 数学与信息科学学院, 陕西 咸阳 712000;
3. 西北工业大学 航海学院, 西安 710072
为了提高求解欧拉(Euler)方程和纳维-斯托克斯(NS)方程的计算效率,结合隐式时间离散格式研究了间断伽辽金有限元方法(DGM).通过改进上下三角分解对称高斯赛德尔(LU-SGS)格式,引入舍入误差项,构造了超松弛内迭代LU-SGS离散格式,实现了非定常可压缩绕流流场的计算.通过Sod激波管问题、二维管道问题验证了算法的可靠性和准确性.数值计算了RAE2822翼型、ONERA M6机翼跨声速可压缩绕流问题,并与多步龙格库塔(RK)算法、LU-SGS算法和广义极小残余(GMRES)算法的计算结果进行了比较.结果表明,超松弛内迭代LU-SGS算法具有良好的稳定性和高效性,计算效率是LU-SGS格式的2.35~3.1倍,是RK格式的5.4倍.
2. School of Mathematics and Information Science, Xianyang Normal University, Xianyang 712000, China;
3. School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
In order to improve the computational efficiency of solving Euler equation and Navier-Stokes equation, the discontinuous Galerkin finite element method was investigated by combining with the implicit time discrete scheme. The lower upper-symmetric Gauss-Seidel(LU-SGS) scheme was improved through retaining the round-off error item, and an overrelaxation interior iteration LU-SGS discrete scheme was constructed to realize the calculation of unsteady compressible flow fields. The reliability and accuracy of the algorithm were verified by solving the Sod shock tube problem and the two-dimensional pipeline problem. The transonic compressible flows around RAE2822 airfoil and ONERA M6 wing were numerically calculated, and the results were compared with that of the multistep Runge-Kutta(RK) algorithm, LU-SGS algorithm and generalized minimal residual algorithms(GMRES). The results show that the presented algorithm has good stability and efficiency, and its computational efficiency is 2.35~3.1 times that of LU-SGS scheme and 5.4 times that of RK scheme.
自20世纪70年代Reed和Hill[1]求解中子运输问题提出间断伽辽金有限元方法(DGM, discontinuous Galerkin finite element method)以来,该方法已经广泛应用于求解浅水波方程(KdV, Korteweg-de Vries equation)、声波方程、对流-扩散方程,逐渐应用于航空、航天、石油勘探、气象预测等领域.尤其是Cockburn等[2-3]自1989年以来研究的系列成果,开创性地提出了龙格-库塔(RK, Runge-Kutta)间断Galerkin有限元方法,构建了求解双曲守恒律方程的基本框架. Rhebergen等[4]采用混合有限元算法求解了不可压缩纳维-斯托克斯(NS, Navier-Stokes)方程.有限体积方法实现高阶重构需要较大的计算模板,因此张来平等[5]研究了高阶精度数值方法,在非结构/混合网格上提出了间断伽辽金/有限体积(DG/FV, discontinuous Galerkin/finite volume)混合算法,实现了Euler方程的计算,提出了“动态、静态重构”方法构造高精度方法,并推广应用于二维NS方程的求解. Filbet等[6]考虑到颗粒碰撞,对稀薄气体多尺度动力学方程引入简化探测器,用于区分动力学和流体区域,充分利用DGM的紧致特性,发展了非常适合于耦合界面动力学和流体模型的间断有限元算法.值得注意的是,Luo等[7-8]提出的重构DG方法在DG方法的框架下保留了DG方法的优点,重构原有解函数的自由度,达到高阶精度.近年来,通过计算流体力学(CFD, computational fluid dynamics)研究者的不懈努力,丰富和发展了DGM,并广泛应用于各类工程计算.
DGM具有灵活处理复杂边界、几何区域以及易于并行计算等诸多优点,可以通过提高单元内部分片多项式次数实现任意阶的代数精度.当然DGM也有不足之处,相对于有限体积方法计算量更大,对于计算机计算能力和存储空间需求更高,因此需要结合隐式时间推进方法或结合加速技术的显式推进方法进一步提高计算效率.
CFD计算效率主要受时间离散格式的制约,相对于步长受限制、收敛速度低的显式格式而言,隐式格式往往可以无条件稳定,能够实现大步长推进求解.近年来Newton-Krylov方法逐渐得到了广泛应用,与其他基于近似分解的隐式格式对比发现,Newton-Krylov具有更高的计算效率.康忠良等[9]将广义极小残余算法(GMRES, generalized minimal residual algorithm)应用于求解雷诺平均NS(RANS, Reynolds average NS)方程.姜跃文等[10]在非结构网格上研究了GMRES方法,并应用于翼型设计.党亚斌等[11]采用链式法则精确求解了黏性和无黏通量的Jacobian矩阵,从而提出了解析Jacobian矩阵的GMRES,不仅提高了稳定性,而且提高了计算效率.因此,仅依赖于物理流动机理的隐式格式成为更好的选择.
分析了上下三角分解对称高斯赛德尔(LU-SGS, lower upper-symmetric Gauss Seidel)算法的舍入误差项,加入超松弛迭代技术,构造了适合于二维/三维双曲守恒律方程的隐式DG方法.通过Sod激波管问题、二维管道问题验证了算法的可靠性.通过RAE2822翼型和ONERA M6机翼绕流问题对GMRES格式、LU-SGS格式、多步RK格式以及笔者改进算法进行了分析比较,结果表明,改进算法的计算效率得到了明显提升,且节约了计算资源.
1 计算模型忽略外部热源和体积力,直角坐标系下非定常可压缩Euler方程可表示为
| $ \frac{{\partial \mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{x}},t)}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{x}},t)} \right)}}{{\partial {x_k}}} = 0 $ | (1) |
Q、F定义如下:
| $ \mathit{\boldsymbol{Q}} = \left( {\begin{array}{*{20}{c}} \rho \\ {\rho {u_i}}\\ {\rho e} \end{array}} \right),\quad {\mathit{\boldsymbol{F}}_j} = \left( {\begin{array}{*{20}{c}} {\rho {u_j}}\\ {\rho {u_i}{u_j} + p{\delta _{ij}}}\\ {{u_j}(\rho e + p)} \end{array}} \right) $ |
其中:ρ为气体密度,e为单位体积总内能,p为压强,ui为xi方向的速度,δij是Kronecker符号.
考虑理想气体状态方程,得到压强表达式:
| $ p = {\rm{ }}(\gamma - {\rm{ }}1)\rho (e - \frac{1}{2}{u_j}{u_j}) $ |
其中:空气比热比γ=Cp/Cv=1.4,Cp为定压比热比,Cv为定容比热比.
2 算法推导 2.1 空间离散格式由DG有限元方法对式(1)进行空间离散,左右两侧乘以试验函数Φ,并在积分区域Ω上分部积分,可得方程的弱解形式:
| $ \begin{array}{*{20}{c}} {\int_\mathit{\Omega } {\frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial t}}} \mathit{\Phi }{\rm{d}}\mathit{\Omega } - \int_\mathit{\Omega } {{\mathit{\boldsymbol{F}}_\mathit{k}}} \left( \mathit{\boldsymbol{Q}} \right)\frac{{\partial \mathit{\Phi }}}{{\partial {x_k}}}{\rm{d}}\mathit{\Omega } + \int_\mathit{\Gamma } {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( \mathit{\boldsymbol{Q}} \right)} {\mathit{\boldsymbol{n}}_\mathit{k}}\mathit{\Phi }{\rm{d}}\mathit{\Gamma } = 0,}\\ {\forall \mathit{\Phi } \in V} \end{array} $ | (2) |
其中:Γ为Ω的单元边界,单位外法向量为nk=(nx, ny, nz).划分计算区域Ω为任意形状互不重叠的分片子区域Ωe,因此定义有限元空间为
| $ V_h^p = {\rm{ }}\{ h \in {[{L^2}(\mathit{\Omega })]^m}:h{|_{{\mathit{\Omega }_e}}} \in [V_p^m];\forall {\mathit{\Omega }_e} \in \mathit{\Omega }\} $ | (3) |
其中局部函数空间Vhp是由间断的p阶向量多项式所组成的集合,多项式次数为p(p=1,2,…),m为向量的维数. Vpm定义如下:
| $ V_p^m = {\rm{span}}\left\{ {\prod {x_i^{{a_i}}:0 \le {a_i} \le p,0 \le i \le d} } \right\} $ | (4) |
其中d为空间维数.对每个单元Ωe应用弱解方程(式(2)),得到半离散方程:
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\int_{{\mathit{\Omega }_\mathit{e}}} {{\mathit{\Omega }_h}{\mathit{\boldsymbol{Q}}_h}} {\rm{d}}\mathit{\Omega } - \int_{{\mathit{\Omega }_\mathit{e}}} {{\mathit{\boldsymbol{F}}_k}\left( {{\mathit{\boldsymbol{Q}}_h}} \right)} \frac{{\partial {\mathit{\Phi }_\mathit{h}}}}{{\partial {x_k}}}{\rm{d}}\mathit{\Omega + }}\\ {\int_{{\mathit{\Gamma }_\mathit{e}}} {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( {{\mathit{\boldsymbol{Q}}_h}} \right)} {\mathit{\boldsymbol{n}}_\mathit{k}}{\mathit{\Phi }_h}{\rm{d}}\mathit{\Gamma } = 0,\forall {\mathit{\Phi }_h} \in V_h^p} \end{array} $ | (5) |
其中Qh、Φh分别为解析解Q和试验函数Φ的有限元近似解,由p次分段多项式函数近似,在单元界面之间允许间断.在每个计算单元中,Qh、Φh表达式为
| $ {\mathit{\boldsymbol{Q}}_h} = \sum\limits_{j = 1}^N {{Q_j}\left( t \right)\varphi _j^p\left( x \right),} {\mathit{\Phi }_h} = \sum\limits_{j = 1}^N {{\mathit{\Phi }_j}\varphi _j^p\left( x \right)} $ | (6) |
其中N为多项式空间的维数.那么式(5)对于所有基函数φjp(x)均能成立,代入可得
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\int_{{\mathit{\Omega }_\mathit{e}}} {\varphi _j^p\left( x \right){\mathit{\boldsymbol{Q}}_h}} {\rm{d}}\mathit{\Omega } - \int_{{\mathit{\Omega }_\mathit{e}}} {{\mathit{\boldsymbol{F}}_k}\left( {{\mathit{\boldsymbol{Q}}_h}} \right)} \frac{{\partial \varphi _j^p\left( x \right)}}{{\partial {x_k}}}{\rm{d}}\mathit{\Omega + }}\\ {\int_{{\mathit{\Gamma }_\mathit{e}}} {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( {{\mathit{\boldsymbol{Q}}_h}} \right)} {\mathit{\boldsymbol{n}}_\mathit{k}}\varphi _j^p\left( x \right){\rm{d}}\mathit{\Gamma } = 0,1 \le j \le N} \end{array} $ | (7) |
基于间断Galerkin方法的思想,将式(7)第3项中的数值通量Fk(Qh)nk用黎曼通量函数Hk(QhL, QhR, nk)取代,这里,QhL和QhR分别为单元边界左、右侧的守恒状态向量.数值积分公式采用Gauss积分公式,边界上线性、二次和三次基函数分别使用2点、3点和4点插值积分.计算区域上三角形单元采用3点、6点和13点插值积分,对于四边形单元采用4点、9点和16点插值积分.经过处理后,得到如下方程组:
| $ \mathit{\boldsymbol{M}}\frac{{d\mathit{\boldsymbol{Q}}}}{{d{\rm{t}}}} = {\rm{Res}}(\mathit{\boldsymbol{Q}}) $ | (8) |
因此,问题转化成为求解半离散常微分方程式(8).随着计算区域网格量的增加,显式方法效率过低,不能满足计算要求.然而隐式推进格式往往是无条件稳定的,能够实现大步长推进,因此采用隐式时间离散格式求解式(8).
2.2 隐式离散格式显式离散格式和隐式离散格式是CFD中求解复杂流动问题常用的计算手段.相比较而言,隐式离散格式往往是无条件稳定的,对于计算复杂流动问题更加具有优势.
对式(8)采用向后差分离散并进行线化处理,可得方程组MΔQn=Res(Q)n,其中系数矩阵M严格对角占优,分解可得
| $ \begin{array}{*{20}{l}} {(\mathit{\boldsymbol{L}} + \mathit{\boldsymbol{D}} + \mathit{\boldsymbol{U}})\Delta {\mathit{\boldsymbol{Q}}^n} = {\rm{Res}}{{(\mathit{\boldsymbol{Q}})}^n}} \end{array} $ | (9) |
其中L、D、U具体表达式为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_i} = \frac{1}{2}\left\{ {\sum\limits_j {\int_{{\mathit{\Gamma }_{\mathit{ij}}}} {\varphi _k^i\left( {\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{Q}}_j}} \right)}}{{\partial {\mathit{\boldsymbol{Q}}_j}}}{\mathit{\boldsymbol{n}}_{\mathit{ij}}} - } \right.} } } \right.}\\ {{{\left. {\left. {\left| {{\lambda _{ij}}} \right|\mathit{\boldsymbol{I}}} \right)\frac{{\partial {\mathit{\boldsymbol{Q}}_j}}}{{\partial {Q_k}}}{\rm{d}}\mathit{\Gamma }} \right\}}_{k = 1,2, \cdots ,\mathit{N}}},j < i}\\ {{\mathit{\boldsymbol{D}}_i} = \left\{ {\frac{{\int_{{\mathit{\Omega }_\mathit{i}}} {\varphi _k^i\varphi _l^i{\rm{d}}\mathit{\Omega }} }}{{\delta t}} - \int_{{\mathit{\Omega }_\mathit{i}}} {\frac{{\partial \mathit{\boldsymbol{F}}\left( {\mathit{Q}_i^n} \right)}}{{\partial \mathit{Q}_i^n}}\frac{{\partial {\mathit{\boldsymbol{Q}}_i}}}{{\partial {Q_i}}}\nabla \varphi _k^i{\rm{d}}\mathit{\Omega } + } } \right.}\\ {\frac{1}{2}\sum\limits_j {\int_{{\mathit{\Gamma }_{\mathit{ij}}}} {\varphi _k^i\left( {\frac{{\partial \mathit{F}\left( {{\mathit{\boldsymbol{Q}}_i}} \right)}}{{\partial {\mathit{\boldsymbol{Q}}_i}}}{\mathit{\boldsymbol{n}}_{\mathit{ij}}} + \left| {{\lambda _{ij}}} \right|\mathit{\boldsymbol{I}}} \right){{\left. {\frac{{\partial {\mathit{\boldsymbol{Q}}_i}}}{{\partial {Q_k}}}{\rm{d}}\mathit{\Gamma }} \right\}}_{k = 1,2, \cdots ,\mathit{N}}}} } }\\ {{\mathit{\boldsymbol{U}}_i} = \frac{1}{2}\left\{ {\sum\limits_j {\int_{{\mathit{\Gamma }_{\mathit{ij}}}} {\varphi _k^i\left( {\frac{{\partial \mathit{F}\left( {{\mathit{\boldsymbol{Q}}_j}} \right)}}{{\partial {\mathit{\boldsymbol{Q}}_j}}}{\mathit{\boldsymbol{n}}_{\mathit{ij}}} - } \right.} } } \right.}\\ {\left. {\left| {{\lambda _{ij}}} \right|\mathit{\boldsymbol{I}}} \right){{\left. {\frac{{\partial {\mathit{\boldsymbol{Q}}_j}}}{{\partial {Q_k}}}{\rm{d}}\mathit{\Gamma }} \right\}}_{k = 1,2, \cdots ,\mathit{N}}},j > i} \end{array} $ | (10) |
传统的LU-SGS离散格式直接忽略高阶小量(LD-1U)ΔQn.稳态计算时,一般ΔQn较大,计算稳定后ΔQn趋于0;然而瞬态计算时,CFL数偏大会导致系数矩阵对角占优性质变差,舍入误差增大,进而导致稳定性变差.因此保留该项,化简式(9)可得
| $ \begin{array}{*{20}{c}} {(\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}){\mathit{\boldsymbol{D}}^{ - 1}}(\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{U}})\Delta {\mathit{\boldsymbol{Q}}^n} = }\\ {{\mathop{\rm Re}\nolimits} {\rm{s}}{{\left( \mathit{\boldsymbol{Q}} \right)}^n} + \left( {\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{U}}} \right)\Delta {\mathit{\boldsymbol{Q}}_n} = \overset\frown{\text{Res}}{{\left( \mathit{\boldsymbol{Q}} \right)}^n}} \end{array} $ | (11) |
于是采用下、上三角矩阵交替求解可得
| $ \left( {\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}} \right)\Delta {\mathit{\boldsymbol{Q}}^*} = \overset\frown{\text{Res}}{\left( \mathit{\boldsymbol{Q}} \right)^n},\left( {\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{U}}} \right)\Delta {\mathit{\boldsymbol{Q}}^n} = \mathit{\boldsymbol{D}}{\rm{\Delta }}{\mathit{\boldsymbol{Q}}^*} $ | (12) |
为了进一步提高计算效率,在交替求解中采用超松弛加速迭代技术,可得
| $ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{Q}}_i^* = \left( {1 - \omega } \right)\Delta {\mathit{\boldsymbol{Q}}^{\left( {k - 1} \right)}} + \omega {\mathit{\boldsymbol{D}}^{ - 1}}\left[ {\overset\frown{\text{Res}}\left( \mathit{\boldsymbol{Q}} \right)_i^n - } \right.}\\ {\frac{1}{2}\left\{ {\sum\limits_{j < i} {\int_{{\mathit{\Gamma }_{\mathit{ij}}}} {\varphi _k^i\left( {\frac{{\partial \mathit{F}\left( {{\mathit{\boldsymbol{Q}}_j}} \right)}}{{\partial {\mathit{\boldsymbol{Q}}_j}}}{\mathit{\boldsymbol{n}}_{\mathit{ij}}} - \left| {{\lambda _{ij}}} \right|\mathit{I}} \right)\frac{{\partial {\mathit{\boldsymbol{Q}}_j}}}{{\partial {Q_k}}}{\rm{d}}\mathit{\Gamma }} } } \right\}\Delta \mathit{\boldsymbol{Q}}_j^* - }\\ {\frac{1}{2}\left. {\left\{ {\sum\limits_{j > i} {\int_{{\mathit{\Gamma }_{\mathit{ij}}}} {\varphi _k^i\left( {\frac{{\partial \mathit{F}\left( {{\mathit{\boldsymbol{Q}}_j}} \right)}}{{\partial {\mathit{\boldsymbol{Q}}_j}}}{\mathit{\boldsymbol{n}}_{\mathit{ij}}} - \left| {{\lambda _{ij}}} \right|\mathit{I}} \right)\frac{{\partial {\mathit{\boldsymbol{Q}}_j}}}{{\partial {Q_k}}}{\rm{d}}\mathit{\Gamma }} } } \right\}\Delta \mathit{\boldsymbol{Q}}_j^{\left( {k - 1} \right)}} \right]} \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{Q}}_i^{\left( k \right)} = \left( {1 - \omega } \right)\Delta \mathit{\boldsymbol{Q}}_i^* + \omega {\mathit{\boldsymbol{D}}^{ - 1}}\left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over R} e{\rm{s}}\left( \mathit{\boldsymbol{Q}} \right)_i^n - } \right.}\\ {\frac{1}{2}\left\{ {\sum\limits_{j:j < i} {\int_{{\mathit{\Gamma }_{\mathit{ij}}}} {\varphi _k^i\left( {\frac{{\partial \mathit{F}\left( {{\mathit{\boldsymbol{Q}}_j}} \right)}}{{\partial {\mathit{\boldsymbol{Q}}_j}}}{\mathit{\boldsymbol{n}}_{\mathit{ij}}} - \left| {{\lambda _{ij}}} \right|\mathit{I}} \right)\frac{{\partial {\mathit{\boldsymbol{Q}}_j}}}{{\partial {Q_k}}}{\rm{d}}\mathit{\Gamma }} } } \right\}\Delta \mathit{\boldsymbol{Q}}_j^* - }\\ {\frac{1}{2}\left. {\left\{ {\sum\limits_{j:j > i} {\int_{{\mathit{\Gamma }_{\mathit{ij}}}} {\varphi _k^i\left( {\frac{{\partial \mathit{F}\left( {{\mathit{\boldsymbol{Q}}_j}} \right)}}{{\partial {\mathit{\boldsymbol{Q}}_j}}}{\mathit{\boldsymbol{n}}_{\mathit{ij}}} - \left| {{\lambda _{ij}}} \right|\mathit{I}} \right)\frac{{\partial {\mathit{\boldsymbol{Q}}_j}}}{{\partial {Q_k}}}{\rm{d}}\mathit{\Gamma }} } } \right\}\Delta \mathit{\boldsymbol{Q}}_j^{\left( k \right)}} \right]} \end{array} $ | (14) |
其中:ω∈(0, 2)为松弛因子,收敛准则为
| $ \parallel \Delta {\mathit{\boldsymbol{Q}}^{\left( k \right)}} - \Delta {\mathit{\boldsymbol{Q}}^{\left( {k - 1} \right)}}\parallel /\parallel \Delta {\mathit{\boldsymbol{Q}}^{\left( 1 \right)}}\parallel \le \varepsilon $ | (15) |
最终得到Qn+1=Qn+ΔQ(k).
3 数值结果与讨论 3.1 算法验证1) Sod激波管问题
给定Sod问题的初始条件:
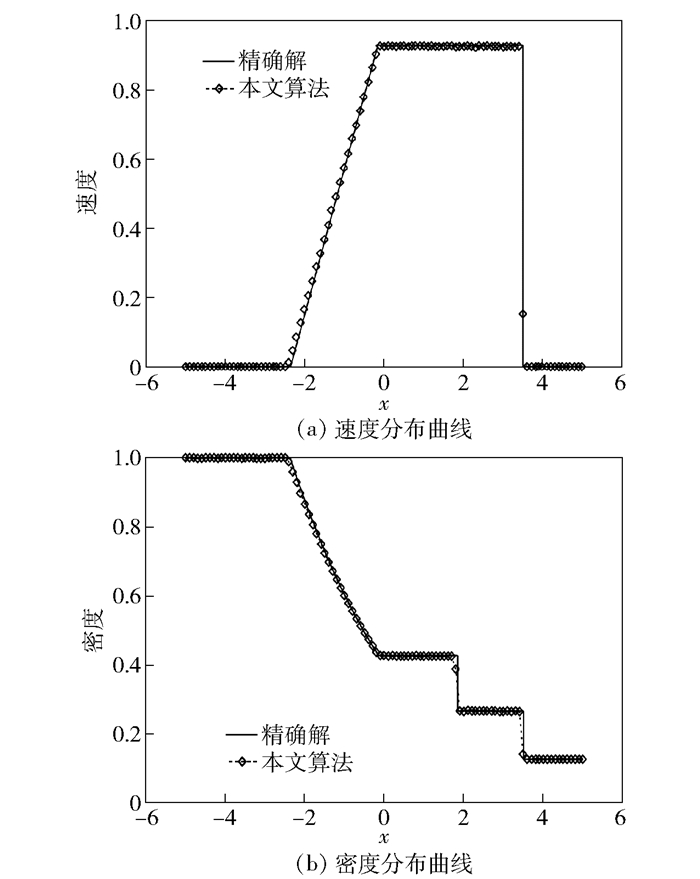
图 1给出了t=2.0时的数值计算结果与精确解比较.显然,本文算法对于激波和接触间断具有良好的捕捉能力,计算精度较高,与实验值吻合良好,验证了算法的正确性和可行性.
|
图 1 Sod激波管数值计算结果与精确解比较 |
2) 二维管道球凸流场问题
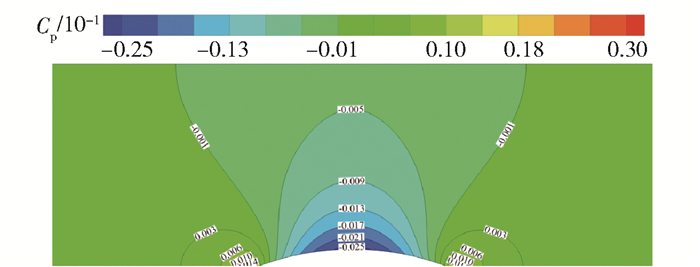
马赫数Ma为0.5,攻角α=0°,计算网格单元总数为32 385. 图 2所示为压力系数分布云图,验证了本文算法的正确性.
|
图 2 二维管道球凸压力系数分布云图 |
本文算例计算中使用设备的基本配置:中央处理器酷睿I5(3. 2 GHz),内存为8 GB.
1) RAE2822翼型跨声速流动
Ma为0.8,α=1.25°,RAE2822翼型网格分布:网格节点13 937,网格单元总数为22 842.
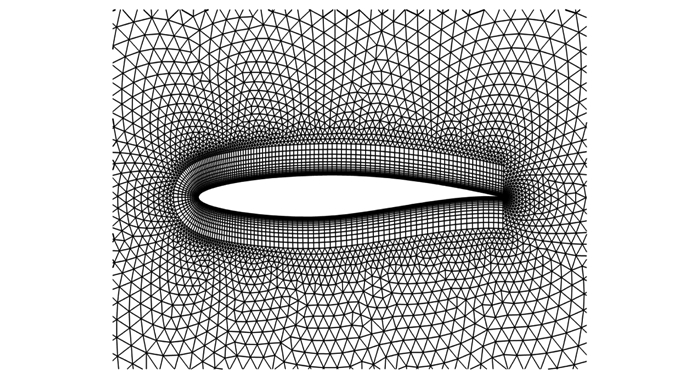
图 3所示为RAE2822翼型局部网格示意图. 图 4给出了翼型表面压力系数分布比较.可以看出,2种不同的隐式算法精度基本一致,与实验结果基本吻合. LU-SGS算法计算时间为4 062步,GMRES算法为971步,本文算法为1 215步,计算时间分别为29.2、11.9、12.4 min. 图 5(a)和(b)分别给出了LU-SGS算法、GMRES算法以及本文算法关于迭代步数与时间收敛历史,可以看出,针对RAE2822翼型绕流计算,本文算法的计算效率相对于传统LU-SGS算法提高了2.35倍,基本接近于GMRES算法,而且占用内存较低.
|
图 3 RAE2822翼型局部网格 |

|
图 4 RAE2822翼型压力系数分布 |

|
图 5 不同隐式时间离散算法的收敛历史比较 |
2) ONERA M6机翼跨声速流动
计算状态:Ma为0.84,α=3.06°,实验雷诺数Re为11.7×106.
整体网格单元总数为582 752. M6机翼表面网格:网格单元总数为36 454,网格节点为18 285.
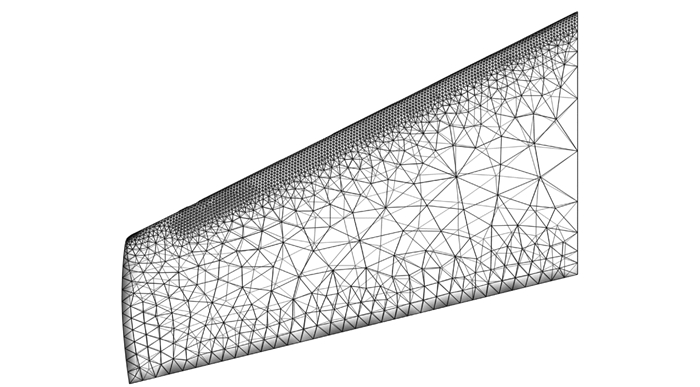
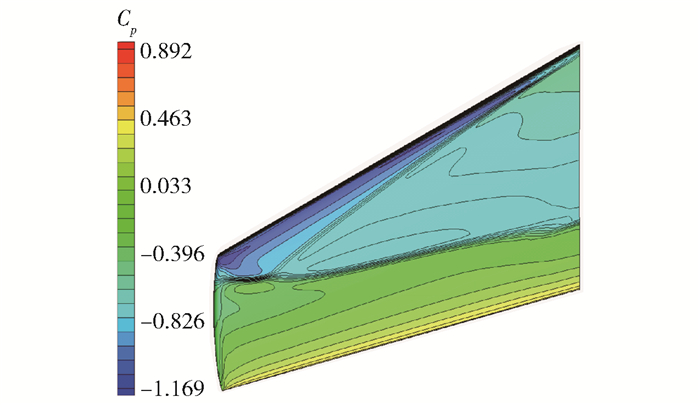
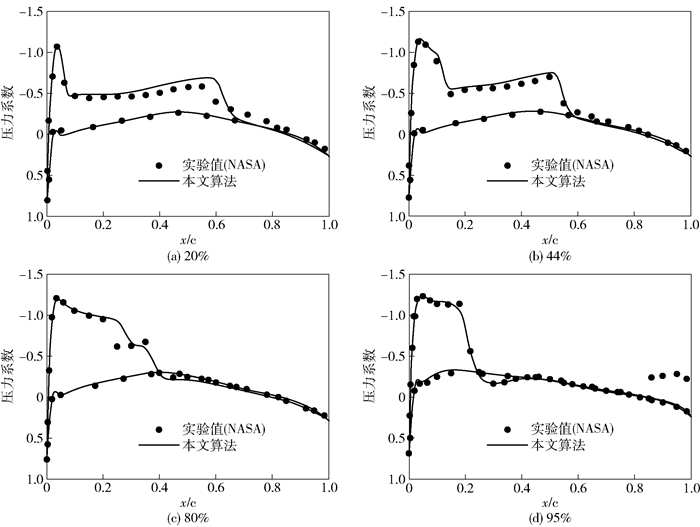
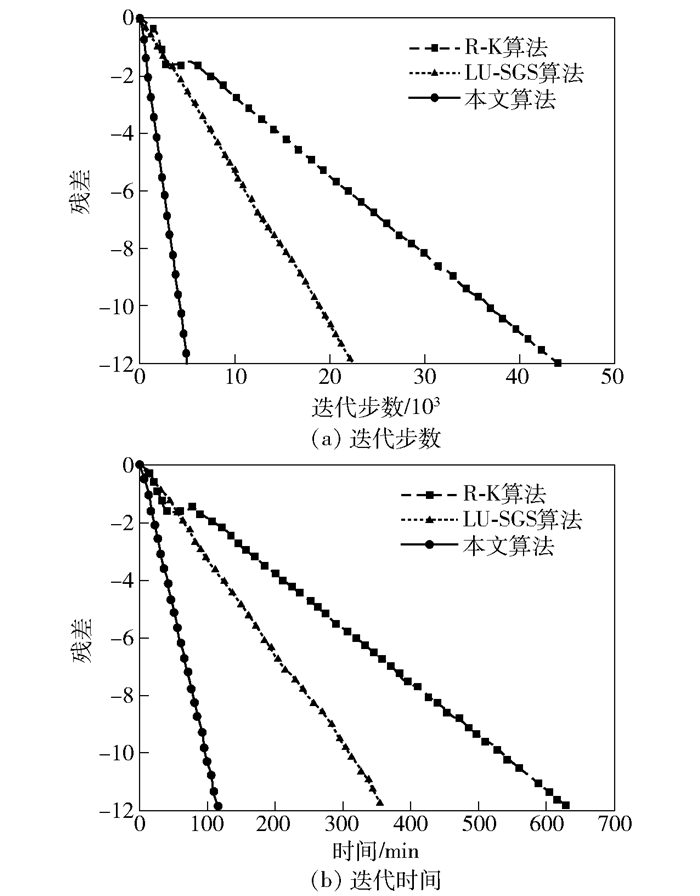
图 6给出了ONERA M6机翼表面网格.从图 7可以看出,本文的计算结果很好地捕捉到γ型激波结构. 图 8给出了不同展向位置处的压力系数对比曲线,可以看出,机翼展向20%、44%、80%和95%占位处压力系数分布均与实验值[12]基本吻合. 图 9(a)和(b)分别给出了3种时间离散格式的收敛历史,显然,本文构造的超松弛LU-SGS方法具有较好的收敛速度,与传统LU-SGS方法相比提高到3.1倍,与RK格式相比提高到近5.4倍,对于复杂绕流问题具有较高的计算效率.
|
图 6 ONERA M6表面网格 |
|
图 7 ONERA M6机翼表面压力系数 |
|
图 8 ONERA M6机翼展向不同站位处压力系数分布 |
|
图 9 不同隐式时间离散算法的收敛历史比较 |
针对显式推进格式计算效率低的问题,通过误差分析而重构算法,构造了隐式超松弛内迭代LU-SGS时间离散间断Galerkin有限元方法.通过算例验证了本文算法的可靠性和准确性,较好地提高了计算效率,得到以下结论.
1) 深入分析误差得到了适合于间断有限元方法的隐式超松弛内迭代LU-SGS算法.数值模拟了RAE2822翼型和ONERA M6机翼跨声速绕流流场,结果与实验值吻合良好,能够准确捕捉流场特征.具有较高的计算效率,能够实现大柯朗-弗里德里奇-列维(CFL, Courant-Friedrichs-Lewy)数的推进计算.
2) 相对于Runge-Kutta算法和LU-SGS算法,本文算法的计算效率分别是Runge-Kutta算法的5.4倍,LU-SGS算法的2.35~3.1倍,计算效率明显提高,基本接近于GMRES算法.在大规模计算中,相对于GMRES算法需要消耗大量的存储空间和空间离散耗时,本文算法是较好的选择,尤其是NS方程的求解问题.
由于本文算法适于实现并行计算[13-14],是下一步工作的重点,也可以结合Yan等[15-16]提供的思路进一步优化算法.
| [1] |
Reed W H, Hill T R. Triangular Mesh methods for the neutron transport equation: LA-UR-73-479[R]. Ann Arbor: Los Alamos Scientific Laboratory Report, 1973.
|
| [2] |
Cockburn B, Shu C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅱ:general frame work[J]. Mathematics of Computation, 1989, 52(186): 411-435. |
| [3] |
Cockburn B, Shu C W. The Runge-Kutta discontinuous Galerkin method for conservation laws Ⅴ:multidimensional systems[J]. Journal of Computational Physics, 1998, 141(2): 199-224. DOI:10.1006/jcph.1998.5892 |
| [4] |
Rhebergen S, Wells G N. A hybridizable discontinuous Galerkin method for the Navier-Stokes equations with pointwise divergence-free velocity field[J]. Journal of Scientific Computing, 2017, 76(3): 1484-1501. |
| [5] |
张来平, 李明, 刘伟, 等. 基于非结构/混合网格的高阶精度DG/FV混合方法研究进展[J]. 空气动力学学报, 2014, 32(6): 717-726. Zhang Laiping, Li Ming, Liu Wei, et al. Recent development of high order DG/FV hybrid methods[J]. Acta Aerodynamica Sinica, 2014, 32(6): 717-726. DOI:10.7638/kqdlxxb-2014.0123 |
| [6] |
Filbet F, Tao X. A hybrid discontinuous Galerkin scheme for multi-scale kinetic equations[J]. Journal of Computational Physics, 2018(372): 841-863. |
| [7] |
Luo H, Luo L, Nourgaliev R. A reconstructed discontinuous Galerkin method for the Euler equations on arbitrary grids[J]. Communications in Computational Physics, 2012, 12(5): 1495-1519. DOI:10.4208/cicp.250911.030212a |
| [8] |
Lou J, Li L, Luo H, et al. Reconstructed discontinuous Galerkin methods for linear advection-diffusion equations based on first-order hyperbolic system[J]. Journal of Computational Physics, 2018(369): 103-124. |
| [9] |
康忠良, 阎超. 适用于混合网格的并行GMRES+LU-SGS方法[J]. 空气动力学学报, 2013, 31(2): 225-230. Kang Zhongliang, Yan Chao. Parallel GMRES+LU-SGS method for mixed grids[J]. Acta Aerodynamica Sinica, 2013, 31(2): 225-230. |
| [10] |
蒋跃文, 叶正寅, 王刚. 基于非结构网格的高效求解方法研究[J]. 计算力学学报, 2012, 29(2): 217-223. Jiang Yuewen, Ye Zhengyin, Wang Gang. Efficient solution of Euler/N-S equations on unstructured grids[J]. Chinese Journal of Computational Mechanics, 2012, 29(2): 217-223. |
| [11] |
党亚斌, 刘凯礼, 孙一峰, 等. 用隐式高精度间断伽辽金方法模拟可压层流和湍流[J]. 空气动力学学报, 2018, 36(3): 535-541. Dang Yabin, Liu Kaili, Sun Yifeng, et al. Implicit high order discontinuous Galerkin method for compressible laminar turbulent flow simulation[J]. Acta Aerodynamica Sinica, 2018, 36(3): 535-541. DOI:10.7638/kqdlxxb-2017.0183 |
| [12] |
Schmitt V, Charpin F. Pressure distributions on the ONERA-M6-wing at transonic Mach numbers[EB/OL]. (1979-05-01)[2019-01-12] http://cf13d.larc.nasa.gov/TestCases/ONERAM6Wing(steady)/exp.dat.
|
| [13] |
Zhou Y, He F Z, Qiu Y M. Optimization of parallel iterated local search algorithms on graphics processing unit[J]. Journal of Supercomputing, 2016, 72(6): 2394-2416. DOI:10.1007/s11227-016-1738-3 |
| [14] |
Zhou Y, He F Z, Qiu Y M. Accelerating image convolution filtering algorithms on integrated CPU-GPU architectures[J]. Journal of Electronic Imaging, 2018, 27(3): 033002. |
| [15] |
Yan X H, He F Z, Chen Y L. A novel hardware/software partitioning method based on position disturbed particle swarm optimization with invasive weed optimization[J]. Journal of Computer Science and Technology, 2017, 32(2): 340-355. DOI:10.1007/s11390-017-1714-2 |
| [16] |
Hou N, He F Z, Chen Y L, et al. An adaptive neighborhood taboo search on GPU for hardware/software co-design[C]//2016 IEEE 20th International Conference on Computer Supported Cooperative Work in Design (CSCWD). Nanchang: [s.n.], 2016: 239-244.
|



