2. 山东交通学院 轨道交通学院, 济南 250357
针对时变无线信道抽头簇的提取和轨迹追踪提出了一种新方法:首先在时延-幅度维上采用反向传播(BP)神经网络对无线信道冲激响应(CIR)进行去噪,然后利用k-means聚类算法对有效抽头信号进行分簇,再用基于密度的空间聚类(DBSCAN)算法去除各个簇峰值抽头中的异常值,最后采用多项式拟合对去除异常值后的簇峰值抽头进行拟合,得到其时间变化轨迹.经过仿真和实测数据验证,该方法得到的簇峰值时间变化轨迹与根据几何关系得到的结果一致.
2. School of Rail Transportation, Shandong Jiaotong University, Jinan 250357, China
A new method for extraction and tracking trajectory of dynamic wireless channel tap clusters is proposed. First, the channel impulse response (CIR) denoising is achieved by back propagation (BP) neural network in time delay-amplitude dimension. Then effective taps are clustered by k-means clustering algorithm. Next, density-based spatial clustering of applications with noise (DBSCAN) algorithm is applied to remove the abnormal peak taps for every cluster. Finally, the trajectory of cluster peak taps is obtained by polynomial fitting. The simulation result shows that trajectory obtained by proposed method is approximate to geometric calculation result. Moreover, the analysis result of high speed railway measured data is consistent with the actual observations.
随着第5代移动通信系统(5G,the fifth generation of mobile communications system)技术的飞速发展,用户对无线传输的要求越来越高.与第4代移动通信系统相比,5G网络主要具有高速率、大容量和低时延三大特点,其传输速率比第4代移动通信系统提升10~100倍,峰值传输速率可达10 Gbit/s,端到端时延达到毫秒级,连接设备密度增加10~100倍,流量密度提升1 000倍,频谱效率提升5~10倍,能够在500 km/h的速度下保证用户有良好地体验[1].这对无线信道的研究提出了更高的要求.
研究无线信道的基础就是对不同场景下的无线信道进行实际测量,并对实测数据进行深入分析,挖掘无线信道衰落特征.传统实测无线信道的研究是基于初级统计理论提取信道参数,不能准确地提取出时变无线信道的特征,因而如何准确地分析无线信道、精准地刻画无线信道模型就成为当前无线通信研究的一大挑战.近几年来,机器学习在各个领域得到了广泛的应用,并取得了巨大的成功,在无线通信的研究中也得到了应用. Chen等[2]使用机器学习来预测信道状态信息,以降低试点开销. Wang等[3]将深度学习应用到通信物理层中的处理,并利用深度学习重新设计传统通信系统的模块,如调制识别、信道解码和检测. Li等[4]提出了一种基于高斯混合模型无线传播信道分簇算法. He等[5]论述了在大数据时代基于聚类的无线信道建模的机遇与挑战,并展示了一些典型聚类算法在信道聚类中的应用.一般而言,信道往往不是静态的,随着车对车(V2V,vehicle to vehicle)通信的迅速发展,时变无线信道的研究也越来越受到关注.以往通过肉眼观察来寻找信道冲激响应(CIR,channel impulse response)簇的轨迹[6],但是该方法不再适用于较复杂的环境. Gentile[7]提出一种基于峰度测量自动识别CIR簇的算法,但是该方法仅仅局限于静态信道. Huang等[8]将轨迹追踪类比成马尔可夫随机过程中的最大后验估计,能在时变信道中有效地实现轨迹追踪.
利用机器学习中的神经网络、k-means聚类和DBSCAN算法,可实现时变无线信道抽头簇的提取和轨迹的追踪,该方法不仅能自动提取并区分CIR中的抽头簇,还能追踪各个抽头簇的时变轨迹,对于精准分析无线信道具有重要意义.
1 理论及方法分析基于机器学习提出了一种无线信道抽头簇的提取和轨迹追踪算法,算法流程下:首先采用反向传播(BP,back propagation)神经网络对单个CIR进行去噪,保留有效抽头信号;然后对有效抽头信号做k-means聚类处理,得到不同的抽头簇,对其他的CIR做相同的操作,得到不同时刻的抽头簇数据;接下来采用基于密度的空间聚类(DBSCAN,density-based spatial clustering of applications with noise)算法去除时变簇峰值抽头中的异常数据,对有效数据做多项式拟合,得到各个簇的时间变化轨迹(后文简称时变轨迹).
1.1 BP神经网络去噪对于多天线无线信道的冲击响应,每个CIR中包含了幅度、时延、Doppler、角度等信息.对于第t帧无线信道快照中的第i个抽头,可表示为
| $ {h^{(t,i)}} = \left( {h_t^{(t,i)},h_\tau ^{(t,i)},h_\Lambda ^{(t,i)},h_{{\theta _{{\rm{AOA}}}}}^{(t,i)},h_{{\theta _{{\rm{AO}}{\rm{D}}}}}^{(t,i)}} \right) $ | (1) |
其中:ht(t, i)表示该抽头所在的时刻,hτ(t, i)表示对应的时延,h(t, i)A表示幅度数值,hθAOA(t, i)表示到达角(AOA,angle of arrival)数值,hθAOD(t, i)表示离开角(AOD,angle of departure)数值.
在对某场景进行信道测量时,会受到热噪声的影响,测量设备误差等因素也导致获取的CIR中会有噪声数据.传统CIR去噪的方法是根据经验值设定一个阈值,当CIR中抽头的幅度超过该阈值,则将该抽头判为有效信号;若该抽头的幅度小于该阈值,则会判为噪声.若阈值过高,噪声会被消除掉,但部分有效信号也会被误判为噪声;若阈值过小,有效信号会被保留下来,但部分噪声会被误判成有效信号,所以传统的硬判决方法并不能准确地实现去噪.如果将CIR去噪看成从信号中区分出有效信号和噪声信号,则可将问题转化成一个二分类的问题.在机器学习中,有许多方法可以处理二分类问题,这里采用BP神经网络的方法.在一个有噪声的CIR中,有效信号都是聚簇存在的,因此若判断一个抽头是否为有效信号,需要考虑其周边抽头幅度的影响[9].对一个抽头进行判断时,也把其周边相邻的6个抽头考虑在内.
3层BP神经网络包括:7个节点的输入层,10个节点的隐含层和一个输出节点的输出层.神经元的激活函数均为sigmod函数.对第i个抽头进行判定时,需要考虑其周边6个点的影响,包含该抽头的前3个点和后3个点,将这7个点作为神经网络的输入. Y(t, i)表示对该抽头的判决结果,取值为0(表示噪声)或者1(表示有效信号).对于CIR中第t个CIR中的第i个抽头h(t, i),将{h(t, i-3), h(t, i-2), …, h(t, i+3), Y(t, i)}这8个数值作为一个样本来处理.
在采用BP神经网络处理数据前,需要对输入的每帧CIR作如下归一化处理:
| $ \overline {h_v^{(t,i)}} = \frac{{h_A^{(t,i)} - \min \left( {h_v^{(t,i)}} \right)}}{{\max \left( {h_v^{(t,i)}} \right) - \min \left( {h_v^{(t,i)}} \right)}} $ | (2) |
其中v表示维度.之后通过误差反向传播和梯度下降法来训练神经网络模型[10].
1.2 k-means聚类分簇无线电波在传播过程中往往会遇到障碍物并发生反射现象,若障碍物尺寸较大,那么经过同一障碍物反射后到达接收端的电波会呈现出一定的“相似性”,即CIR会出现抽头分簇现象.这种相似性体现在CIR部分区域中的抽头幅度接近,对应的AOA与AOD相差不大.抽头簇不仅能反映周边障碍物的分布情况,还可以通过分析簇的时变轨迹得到物体相对移动的信息.在机器学习中可利用聚类算法实现抽头的分簇,采用k-means聚类算法实现该目的.由于k-means聚类算法对初始选取的聚类中心比较敏感[11],而CIR中噪声抽头往往占据较大的比例,导致分簇结果与真实值差异较大.为解决此问题,聚类前先对数据进行BP神经网络去噪处理.该操作不仅能提高运算速率,还能提高聚类分簇准确度.
Czink在文献[12]中定义了多径分量间的距离,即任意两抽头间的距离.该定义涉及多径抽头的AOA、AOD和时延信息,文本将抽头的幅度也考虑在内,定抽头i与j间的距离为
| $ {D_{ij}} = \sqrt {\sum\limits_v {||{D_{v,ij}}|{|^2}} } $ | (3) |
其中:v可为τ、A、θAOA、θAOD,分别表示时延维、幅度维、角度(AOA与AOD)维,各维度距离定义分别为
| $ {D_{\tau ,ij}} = \alpha \frac{{\left| {{\tau _i} - {\tau _j}} \right|}}{{\Delta {\tau _{\max }}}} \cdot \frac{{{\tau _{{\rm{std}}}}}}{{\Delta {\tau _{\max }}}} $ | (4) |
| $ {D_{A,ij}} = \beta \frac{{\left| {{A_i} - {A_j}} \right|}}{{\Delta {A_{\max }}}} \cdot \frac{{{A_{{\rm{std}}}}}}{{\Delta {A_{\max }}}} $ | (5) |
| $ {D_{{\theta _{{\rm{AON}}/{\rm{AOD}}}},ij}} = \frac{\gamma }{2}\left| {\begin{array}{*{20}{c}} {\sin \;{\theta _i}\;\cos \;{\varphi _i} - \sin \;{\theta _j}\;\cos \;{\varphi _j}}\\ {\sin \;{\theta _i}\;\sin \;{\varphi _i} - \sin \;{\theta _j}\;\sin \;{\varphi _j}}\\ {\cos {\theta _i} - \cos {\theta _j}} \end{array}} \right| $ | (6) |
其中:Δτmax和ΔAmax分别表示最大时延差和最大幅度差;τstd、Astd分别表示时延标准差和幅度标准差;θ表示方位角,φ表示仰角;α、β和γ表示时延距离、幅度距离和AOA/AOD距离的权重因子,默认均取1.
1.3 簇峰值抽头轨迹追踪在实际测量中,信道采样率较高,相邻2个CIR的时间间隔非常短,CIR中的簇在短时间内不会消失,因而就会呈现随着时间而变化的轨迹,如图 9中高铁CIR连续变化的轨迹.抽头簇的时变轨迹能反映出信道随时间变化的特性,也从侧面反映出周边散射物体的相对运动轨迹.信噪比较高时,通过肉眼观察能识别出不同的抽头簇及其时变轨迹,但若反射径较多,错误率将会大大增加,而且会消耗大量的人力和时间,所以如何自动追踪簇抽头的时变轨迹问题亟待解决.对于某一抽头簇而言,其峰值抽头的时变轨迹能代表该簇随着时间变化的特征,所以将问题简化为对抽头簇峰值时变轨迹的追踪.

|
图 9 京津城际实测数据处理结果 |
k-means聚类后得到的时变簇峰值抽头中会有部分抽头偏离大部分抽头,一方面是由于受到噪声的影响;另一方面是由于聚类数目过多导致同一簇分被分成了多簇,可将之认定为异常数据.采用机器学习中的DBSCAN算法能去除异常数据.
DBSCAN是一种基于密度的聚类算法[13],它将簇定义为密度相连点的最大集合,能够把具有足够高密度的区域划分为簇,可在噪声的空间数据库中发现任意形状的聚类,能识别出噪声点和异常点.该算法不需要事先设定簇类的数量,只需给定邻域半径ε和密度阈值P,即(ε,P),抽头间的距离仍采用前文中的距离定义.
理想簇的时变轨迹是一条光滑的曲线,但由于噪声、设备测量误差等因素的影响,去除异常值后的簇峰值时变轨迹并不光滑,所以需对数据做平滑处理.可采用多项式拟合对数据做平滑处理.多项式拟合在保证平方误差和最小的条件下拟合出一条光滑的曲线,反映出簇峰值的时变趋势.
总而言之,该算法的核心思想是以研究簇峰值作为切入点,通过神经网络去噪、k-means分簇、DBSCAN对时变簇峰值数据去除异常值,最后利用多项式拟合找出其时变轨迹.
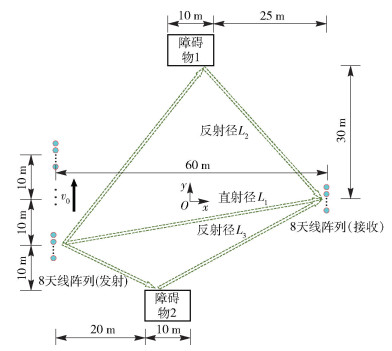
2 算法验证 2.1 仿真验证采用传播图理论[14]生成动态无线信道.仿真场景包含发射天线、接收天线和2个长度为10 m的障碍物,如图 1所示.
|
图 1 仿真场景示意图 |
接收天线位置(30, 0, 20)固定不变,发射天线以36 km/h的速度向y方向移动.发射天线从位置(-30, -10, 1.5)移动到(-30,20, 1.5)位置,2个宽度为10 m的障碍物,其反射面中心分别位于(0, 30, 0)和(-5, -25, 0).仿真频点为5 GHz,带宽为300 MHz,CIR中相邻两抽头对应的距离差为1 m,收发天线采用8×8模式,相邻2个天线间距为半波长.电磁波的传播路径如图 1中的虚线所示.对发射端天线运动轨迹进行均匀抽样,每隔0.1 m仿真一帧信道快照,该运动过程中共生成300帧CIR快照(共3 s).在只考虑一次反射的前提下,利用传播图理论对上述场景进行仿真得到CIR.在实际环境中,信道不可避免地会受到噪声的影响,因而需对生成的CIR做加噪处理,方法如下:每一帧CIR在时延域上卷积长度为2017的Zadoff-Chu(ZC)序列,对输出结果做加高斯白噪声处理,最终用加噪后的数据与源ZC序列做时延域上的相关,便可得到加噪CIR.生成的信噪比为30 dB的CIR如图 2所示.

|
图 2 SNR为30 dB时CIR三维俯视图 |
从图 2可以看出,该CIR的有效信号主要集中在L1、L2、L3这3条曲线周边的区域,3条黑色实线表示根据几何关系得到的抽头时变轨迹. L1表示直射径抽头的时变轨迹.随着发射天线的移动,直射径抽头时延先逐渐减小至200 μs,再逐渐增大. L2表示经过障碍物1的反射后到达接收端的反射径;L3表示信号经过障碍物2的反射后到达接收端的反射径,L2和L3在约1.9 s时刻有交点.
与射线追踪法的信道仿真理论不同的是,传播图信道仿真理论是基于不同点集合(发射、接收、散射)间的频域传递函数获得时延域上的CIR,而且由于漫反射的存在,电磁波在点集合间传播时并不一定完全遵循镜面反射规则.以反射径L3为例,其时延τ与收发天线位置的几何关系计算如下:
| $ \tau = {\rm{ }}({d_{{\rm{TS}}}} + {d_{{\rm{SR}}}})/{\rm{ }}c $ | (7) |
其中:dTS表示发射天线到障碍物反射中心的距离,dSR表示接收天线到障碍物反射中心的距离,c表示光在真空中的速度.对比2个结果可以看出,根据几何计算结果得到的抽头时变轨迹完全可以表示各簇的时变轨迹.
根据1.1节的内容采用BP神经网络对CIR进行去噪处理.训练模型时,选取前5帧CIR快照中的抽头以人工方式打上标签,作为训练数据.训练时采用附加动量法防止陷入局部最优解,其中附加动量因子设为0.2,经过1 000次训练后,均方根误差逐渐趋近稳定值0.13.
图 3中的实线表示发射端移动到(-30,-5, 1.5)m位置时的瞬时快照,此时收发端间隔为63 m,对应时延0.21 μs,CIR最高峰抽头对应时延为0.21 μs,两者结果是一致的. 图 3中的点划线表示对该帧数据采用BP神经网络判别的结果,虚线表示硬判决门限,判决门限取-16 dB.从图 3可以看出,对于部分抽头幅度过高的噪声信号,如区域S中的抽头,传统的方法是将该区域中的抽头判决为有效信号,而神经网络并未将其判决为有效信号.根据图 2中的几何计算结果可知,该区域的抽头应为噪声信号.与传统硬判决方法相比,BP神经网络能较精确地去除CIR中的噪声.

|
图 3 单帧快照BP神经网络去噪结果 |
经过去噪处理后,数据点的数目会大幅度减少.接下来计算出每个抽头对应的AOA和AOD,然后对每帧CIR均采用k-means算法进行分簇.在聚类前需指定聚类数,这里通过手肘法来确定聚类数[15],即通过观察聚类数与平方误差和关系,将拐点处对应的数设为聚类数.经验证,拐点处聚类数为3.
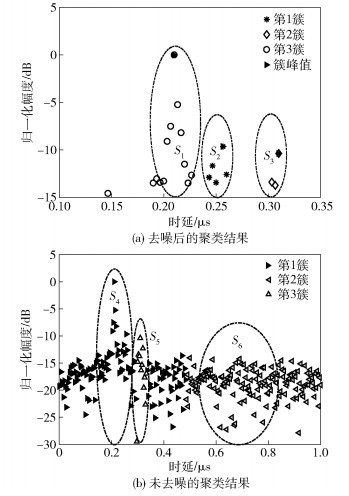
图 4(a)中,设定聚类数为3时k-means聚类算法将抽头点划分成S1、S2、S3共3个有效抽头簇.图中黑三角表示簇峰值抽头,即每个簇内幅度最大的抽头.这3个簇峰值抽头对应的时延分别为0.21 μs、0.256 μs、0.31 μs.几何计算结果对应的时延为0.21 μs、0.247 μs和0.31 μs,对比2个结果可知,聚类后各个簇峰值抽头的时延数值与几何计算结果几乎一致. 图 4(b)所示为对未去噪CIR聚类得到的结果,聚类数目为3.从图中可知,抽头被分成了S4、S5、S6共3簇.对比图 4(a)可知,簇S4包含了2个有效抽头簇,而S6包含的均是噪声,聚类结果的均一性较差.因而先去噪后聚类的方案是可行的.
|
图 4 聚类结果(聚类数为3) |
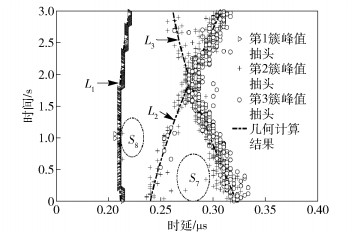
类似地,对每帧CIR做相同的操作后,便可得到该场景整个过程中簇峰值的时变轨迹,如图 5所示.其中3条线L1、L2与L3表示根据几何计算得到的簇峰值时变轨迹,可以看出,经过去噪、聚类后得到的簇峰值抽头沿时间变化的趋势与几何计算结果一致,两者对应的时延范围也基本一致.但图中有两部分数据是错误的,一是由于噪声的影响,部分噪声抽头被误判成有效抽头,这部分数据可认定为异常数据;二是抽头所属簇判别错误.采用DBSCAN算法可解决上述2个问题.
|
图 5 各帧CIR的k-means聚类结果 |
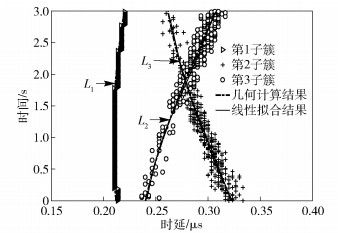
将聚类后所有簇峰值抽头作为DBSCAN输出数据,设定DBSCAN参数(ε, P)为(0.06, 4),对聚类后得到的多个子集按子集内抽头的数目进行降序排序,取数目最多的3个子集,得到的结果如图 6所示.可以看出,对于第1子集数据与处理前L1附近的数据基本一致;第2、3子集经过处理后,去除掉了一些异常数据,保留下能反映数据变化趋势的数据.对上述3个子集,以有效抽头对应的时间为自变量,对应的时延为因变量,经过5次多项式拟合,结果如图中实线所示.可以看出,拟合结果与几何计算结果得到的时变轨迹趋势一致.经计算可得,时延的均方根误差(RMSE, root mean square deviation)为833.7 μs,平均绝对百分误差(MAPE, mean absolute percentage error)为3.2%,所以该方法得到的3条曲线能代表 3个簇的时变轨迹.
|
图 6 DBSCAN处理结果 |
前文通过传播图信道建模理论从理论上证明了该方案的可行性,下面将采用该方案对高速铁路无线信道测量数据进行分析.测试地点位于京津城际铁路沿线永乐店附近,采用无线信道探测设备PropSound进行实地单天线信道测量,测试点到轨道垂直距离约为82.5 m,测量频点为2.35 GHz,带宽为10 MHz.接收天线采用车载天线HUBER+SUHNER,其位于0号测试车顶部.发射天线采用偶极子天线,其位于测试点,天线架高15 m,发射功率为37 dBm,采用127阶的m序列作为激励信号,利用相关器获取信道的冲击响应信息[16].测试方案和场景如图 7所示.

|
图 7 测试场景示意图 |
场景周围是平坦的近似乡村场景,反射障碍物较少. 0号车运行到测试点位置的速度约为240 km/h,测试车从远端逐步靠近基站,然后离开基站.该过程持续时间约为65 s. 图 8所示为在该场景下实测的CIR变化.可以看出,随着列车逐渐靠近基站,时延越来越小,且CIR中的多径分量越来越多;在接近区域CA1中反映最为明显,大约在37 s区域AA附近存在一个较强的直射径,该直射径对应的时延最小,表明列车此刻距离基站最近;37 s之后列车逐渐远离基站,直射径对应的时延逐渐变大,在离开区域CA2中多径分量也逐渐增多.整个过程中区域CA1与CA2中的多径分量较多.接下来对该数据做分析.由于测量过程中采用的是单天线,所以将抽头距离定义中与角度有关的因子γ均设为0.

|
图 8 京津城际沿线实测CIR变化 |
首先对该数据采用BP神经网络进行去噪,然后采用k-means算法对去噪后的数做聚类分析.由图 8可知,整个过程中CIR主要包含了一个明显的主径分量和部分反射分量,反射分量如CA1与CA2区域中的抽头,利用手肘法设定聚类数目为2.经过k-means聚类算法处理后结果如图 9(a)所示.
图中部分区域中的两簇峰值数据距离非常近,如区域A中的抽头.这是由于设定的聚类数目为2,导致同一簇抽头分成两簇,所以两簇峰值距离比较近.采用DBSCAN聚类算法对这两簇数据做去异常处理,设定参数(ε, P)为(0.003, 4),取聚类后抽头数目最多的10个子集,得到如图 9(b)的结果.由图可知,第1子集基本能体现出直射径的变化趋势,其他的子集包含了一些次要信息,如第3子集表示周边散射物的影响,取第1子集的数据进行下一步的拟合操作.
取多项式拟合阶数为3,则可得到接近基站与离开基站2个过程中抽头时延τ与时间t关系式如下:
τ=[P1 P2]T= P1T, t < 36.59接近基站
| $ \tau =\left[ {{P_1}\;{P_2}} \right]T = \left\{ \begin{array}{l} {P_1}T,\;t < {\rm{ }}36.{\rm{ }}59\;接近基站\\ {P_2}T,\;t \ge 36.{\rm{ }}59\;离开基站 \end{array} \right. $ | (8) |
其中,T =[1 t t2 t3]T,系数P1与P2数值如下:
| $ \begin{array}{l} \left[ {{P_1}\;{P_2}} \right] = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {4.61 \times {{10}^{ - 6}}} \end{array}}&{ - 4.72 \times {{10}^{ - 7}}}\\ { - 1.07 \times {{10}^{ - 7}}}&{ - 7.21 \times {{10}^{ - 8}}}\\ { - 3.4 \times {{10}^{ - 10}}}&{3.69 \times {{10}^{ - 9}}}\\ {7.57 \times {{10}^{ - 12}}}&{ - 2.44 \times {{10}^{ - 11}}} \end{array}} \right]^{\rm{T}}} \end{array} $ | (9) |
从图 9(b)可知,第1子集与肉眼观察到直射径分量的时变轨迹是一致的,因而可将最终多项式拟合结果作为直射抽头簇的时变轨迹.
3 结束语基于机器学习算法提出了一种无线信道抽头簇轨迹追踪的方法.仿真结果表明,该方法能准确地去除CIR中的噪声,对抽头有效地分簇,并拟合出簇峰值抽头的时变轨迹.对比已知的几何结果,MAPE为3.2%,验证了所提算法的合理性与准确性,并用该方法对高铁实测数据进行了分析,得到的结果与人为观测结果一致.这对于精准研究分析时变无线信道具有重要意义.
| [1] |
Gupta A, Jha R K. A survey of 5G network:architecture and emerging technologies[J]. IEEE Access, 2015(3): 1206-1232. |
| [2] |
Chen L, Haihan L, Yunzhou L, et al. A learning-based channel model for synergetic transmission technology[J]. China Communications, 2015, 12(9): 83-92. DOI:10.1109/CC.2015.7275262 |
| [3] |
Wang T, Wen C K, Wang H, et al. Deep learning for wireless physical layer:opportunities and challenges[J]. China Communications, 2017, 14(11): 92-111. DOI:10.1109/CC.2017.8233654 |
| [4] |
Li Y, Zhang J, Ma Z. Clustering in wireless propagation channel with a statistics-based framework[C]//Wireless Communications and Networking Conference (WCNC), 2018 IEEE. Barcelona: IEEE, 2018: 1-6.
|
| [5] |
He R, Ai B, Molisch A F, et al. Clustering enabled wireless channel modeling using big data algorithms[J]. IEEE Communications Magazine, 2018, 56(5): 177-183. DOI:10.1109/MCOM.2018.1700701 |
| [6] |
Yu K, Li Q, Cheung D, et al. On the tap and cluster angular spreads of indoor WLAN channels[C]//Vehicular Technology Conference, 2004, VTC 2004-Spring, 2004 IEEE 59th. Milan: IEEE, 2004: 218-222.
|
| [7] |
Gentile C. Using the Kurtosis measure to identify clusters in wireless channel impulse responses[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(6): 3392-3395. DOI:10.1109/TAP.2013.2253299 |
| [8] |
Huang C, He R, Zhong Z. A novel power weighted multipath component tracking algorithm[C]//General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), 2017 XXXIInd. Montreal: IEEE, 2017: 1-4.
|
| [9] |
Ma X, Zhang J, Zhang Y, et al. Data scheme-based wireless channel modeling method:motivation, principle and performance[J]. Journal of Communications and Information Networks, 2017, 2(3): 41-51. |
| [10] |
Pineda F J. Generalization of back-propagation to recurrent neural networks[J]. Physical Review Letters, 1987, 59(19): 2229. DOI:10.1103/PhysRevLett.59.2229 |
| [11] |
Hartigan J A, Wong M A. Algorithm AS 136:a k-means clustering algorithm[J]. Journal of the Royal Statistical Society, Series C (Applied Statistics), 1979, 28(1): 100-108. |
| [12] |
Czink N, Cera P, Salo J, et al. Improving clustering performance using multipath component distance[J]. Electronics Letters, 2006, 42(1): 33-35. |
| [13] |
Schubert E, Sander J, Ester M, et al. DBSCAN revisited, revisited:why and how you should (still) use DBSCAN[J]. ACM Transactions on Database Systems (TODS), 2017, 42(3): 19. |
| [14] |
Pedersen T, Fleury B H. A realistic radio channel model based in stochastic propagation graphs[C]//5th Conf on Mathematical Modelling (MATHMOD 2006). Vienna: ARGESIM, 2006: 324-331.
|
| [15] |
Thorndike R L. Who belongs in the family?[J]. Psychometrika, 1953, 18(4): 267-276. DOI:10.1007/BF02289263 |
| [16] |
Liu L, Tao C, Qiu J, et al. Position-based modeling for wireless channel on high-speed railway under a viaduct at 2.35GHz[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(4): 834-845. DOI:10.1109/JSAC.2012.120516 |



